Лабораторная работа №4 изучение вращательного движения на приборе обербека

Задания:

1. определить момент инерции крестообразного маятника без дополнительных грузов;

2. проверить основное уравнение динамики вращательного движения;

3. изучить зависимость момента инерции крестообразного маятника от положения грузов на стержнях;

4. экспериментально проверить теорему Штейнера.

Приборы и принадлежности: маятник Обербека, секундомер, штангенциркуль, набор грузов, линейка.

Элементы теории

Простейшим видом вращательного движения твердого тела является вращательное движение вокруг неподвижной оси, при котором все точки тела, двигаясь в параллельных плоскостях, описывают окружности с центрами, лежащими на одной неподвижной прямой, перпендикулярной плоскости этих окружностей, называемой осью вращения.

При вращении твердого тела вокруг неподвижной оси все частицы тела совершают плоское движение, причем линейные скорости и ускорения частиц вообще различны. Угловая скорость вращения для всех частиц тела будет одинакова и определяется выражением

, =рад/с, (1)

где - есть первая производная от угла поворота по времени.

Направление угловой скорости определяется по правилу правого винта: вращая винт по направлению вращения твердого тела или материальной точки, поступательное движение винта указывает на направление (рис.1).

Рис. 1

Если угловая скорость вращения изменяется во времени, то ее изменение можно характеризовать угловым ускорением

, рад/с², (2)

где - есть первая производная от угловой скорости по времени.

Направление совпадает с направлением , если движение ускоренное, и противоположно, если движение замедленное.

Для заданного вращающегося тела угловое ускорение определяется действием суммы моментов сил. Моментом сил называется физическая величина, определяемая векторным произведением радиус-вектора на вектор действующей силы :

, (3)

Нм.

Направление вектора момента сил определяется по правилу векторного произведения (правилу правого винта): вращая винт от первого вектора ко второму , поступательное движение винта указывает на направление вектора (рис. 2).

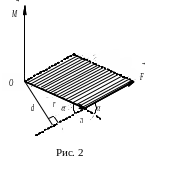
Модуль вектора определяется как

(4)

и численно равен площади параллелограмма (заштрихованной фигуры) (рис. 2). Учитывая, что , можно записать

, (5)

где − плечо силы, т.е. кратчайшее расстояние от точки О, относительно которой происходит вращение, до линии действия силы .

При рассмотрении момента сил относительно оси Оz необходимо спроектировать векторное произведение на эту ось, т.е.

. (6)

Разложим силу (рис. 3) на три взаимно перпендикулярные составляющие: - параллельную оси Oz, - перпендикулярную к оси Oz и - перпендикулярную к плоскости, проходящей через ось и точку приложения силы.

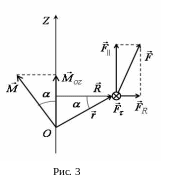
Если представить окружность радиуса R с центром на оси Oz, то составляющая будет направлена по касательной к этой окружности. Тогда момент силы относительно точки О будет равен сумме моментов составляющих сил: . Векторы и перпендикулярны к оси Oz, поэтому их проекции на эту ось равны нулю. Момент имеет модуль и образует с осью Oz угол α, косинус которого равен отношению . Следовательно, момент силы относительно оси Oz имеет величину . Таким образом, момент силы относительно оси Oz равен .

Для нахождения связи между угловым ускорением тела и моментом сил , действующих на него, рассмотрим движение одной какой-то частицы вращающегося тела (рис. 4).

Пусть частица с массой находится на расстоянии от оси вращения Oz. На частицу могут действовать как внутренние, так и внешние силы. Внешние силы приложены со стороны других тел, а внутренние – со стороны частиц того же самого тела.

Обозначим проекцию суммы внутренних сил, действующих на , на направление, перпендикулярное к , как , а проекцию суммы внешних сил как . Тогда, применяя 2-ой закон Ньютона к каждой точке вращающегося тела, можно записать:

, (7)

где – линейное ускорение частицы.

Если умножить выражение (7) на и учесть, что , то получим:

, (8)

где - проекция углового ускорения на ось Oz.

Величина , численно равная произведению массы на квадрат расстояния ее от оси вращения, называется моментом инерции материальной точки относительно оси вращения.

Величины и определяют моменты внутренних и внешних сил, действующих на -ю частицу тела.

Уравнения типа (7) и (8) можно записать и для остальных частиц тела. Суммируя выражение (8) по всем элементам тела, получим:

, (9)

где - сумма проекций на ось Oz всех внутренних моментов сил ( , т.к. каждая внутренняя сила имеет равную и противоположную себе силу, приложенную к другой частице тела с тем же самым плечом);

- сумма проекций на ось Oz всех внешних моментов сил, приложенных к телу;

- момент инерции твердого тела относительно оси вращения Оz, равный сумме моментов инерции отдельных частиц тела ( кгм²).

Использовав все обозначения, получим:

, (10)

откуда

(11)

 основной закон динамики вращательного движения.

В векторном виде этот закон может быть записан в виде:

, (12)

то есть угловое ускорение пропорционально действующему внешнему моменту сил и обратно пропорционально моменту инерции твердого тела относительно оси вращения.

Этот закон аналогичен закону динамики для поступательного движения

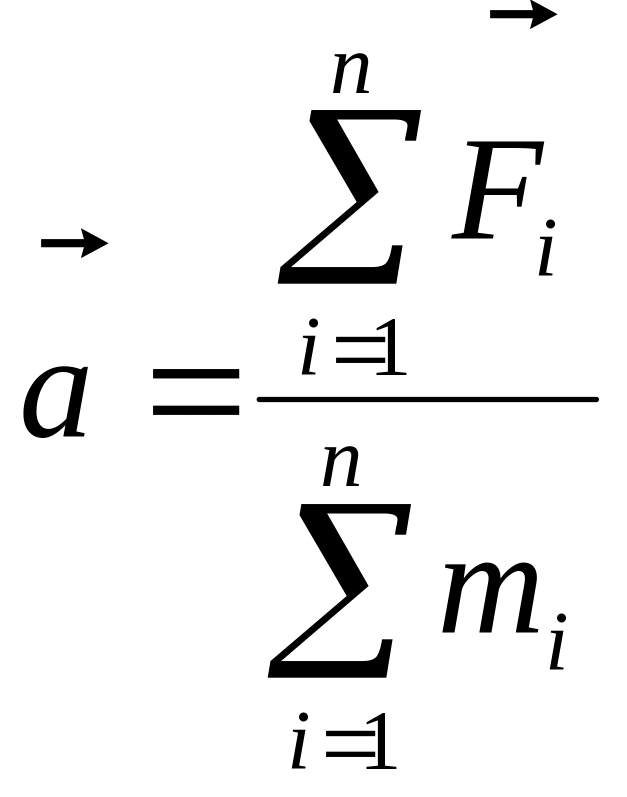, (13)

где - линейное ускорение;

- сумма всех внешних сил;

- сумма всех элементарных масс.

Используя аналогию, можно сделать вывод о том, что момент инерции при вращательном движении играет такую же роль, как и масса при поступательном движении, т.е. момент инерции является мерой инертности тела при вращательном движении.

Проверка основного закона вращательного движения и определение момента инерции производится на приборе, называемом маятником Обербека (рис. 5).