Пространство желаемых событий.
Рассмотрим некоторую группу( систему) S событий A, B, C…, каждое из которых при осуществлении комплекса условий «сигма» может произойти или не произойти , тогда между событиями группы S устанавливается следующее соотношение:
1 Если вслед за
наступлением события A
всегда наступает B,
то полагается, что A
влечет за собой B.
И обозначается символом: AcB,
(1)
2 Если A влечет B, и B влечет A, то A и B!= равносильными. A=B (2)
3 Событие, состоявшееся
в наступлении обоих событий A
и B:=
произведением (пересечением) событий
A*B,
(3)
4 Событие, состоящее
в наступлении хотя бы одного из событий
A
и B:
= объединением событий. A+B,
5 Событие, состоящее в том, что A происходит, а B – не происходит: = разностью событий A и B. A-B, A\B (5)
6 Событие,
дополнительно с A
обозначается
или A^c.
7 Событие A и B: = несовместимыми (непересекающимися), если их совместное осуществление невозможно.
# несовместимыми являются события A-b и B
Геометрическая трактовка различных событий представлена диаграммой Вьена, для которой: - комплекса условий «сигма»: внутри квадрата есть две окружности и наудачу выбрана точка;
Событие A: точка лежит внутри левой окружности;
Событие B:
точка лежит внутри правой окружности.
Тогда события A,
,
B,
,
A+B
(
),
AB,
следующие состоят в воображаемой точки
внутрь соответствующих областей.
В каждой задаче теории вероятности приходится иметь дело с некоторым комплексом условий «сигма» и группой (системой) событий S.
Группа (система) несовместимых событий A1, A2…An, из которых одно обязательно происходит: = полной группой событий.
Группа (система) S событий, содержащих: 1 наряду с каждой принадлежащих ей событий A,B, также события AB, A+B, A-B (6). 2 достоверное и невозможное событие: = полем событий S.
Если каждый, неразложимый исход, идеализированного опыта, представлен только один элементарным событием w_i, то совокупность всех элементарных событий {w_1, w_2, …}: = пространством элементарных событий «омега», а сами элементарные события w_i – точками пространства «омега».
Определение вероятности и её типы.
Наряду с простым установлением закономерностей, распространены явления, для которых доля части случаев, когда A происходит, лишь несколько отклоняются от некоторого усредненного значения. Для таких явлений возможна количественная ?аниса? возможности появления события, выраженного выражением: вероятность того, что при осуществлении комплекса условий «сигма» произойдет A = p. Так, устанавливаемы закономерности: = вероятностными или стохастическими. Идея о том, что вероятность случайного события A при известных условиях допускает количественную оценку при помощи некоторого числа p = P(A) получило систематичное развитие в работах Ферма (1601-1665) и т.д.
Классическое определение вероятности.
Вероятность события A, включающего m событий из входящей в поле событий S ?колиой? группы n элементарных событий w_1,…, w_n, = P(A)=m\n (7)
Или: Вероятность события A равно отношению числа возможных результатов испытания, благоприятствующих событию A, к числу всех возможных результатов испытаний.
# При бросании игральной кости событие A: выпадение четного числа очков, - представлено в виде: A=w_2 + w_4 + w_6 включающим три случая, входящих в полную группу несовместимых и равновероятностных событий. Поэтому P(A) = 3\6=0.5.
Четыре типа определения вероятности.
Многочисленные определения вероятности события можно разделить на четыре типа:
Субъективное – «на основе меры» степени уверенности ?позиаломо? субъекта.
Комбинированное – опирающееся на понятие «равновозможности» события.
Статистическое – как частоты появления события при большом числе испытаний.
Современное – на основе аксиоматично вводимой формальной числовой меры.
Понятие о геометрической вероятности.
Во многих случаях классическое определение вероятности, основано на рассмотрении конечной группы равновероятных событий, является недостаточным. Сформулируем общую задачу, которая привела к рассмотрению понятия вероятности.
Пусть на плоскости имеется области G, содержащая другую область с квадрируемой границей. В область G бросается точка и спрашивают чему: чему равна вероятность попадания в область g? При этом выражение «точка бросается в область G» имеет следующий смысл: 1. Брошенная точка может попасть в любую точку области G. 2. Вероятность попасть в любую часть области пропорциональна мере этой части (длина, площадь и т.д.) и не зависит от её расположения и формы.
Тогда, вероятность попадания в область G, при бросании на удачу точки в область G равна p= mes*q\mes*g. mes – площадь.
Свойства вероятностей.
Для каждого события A поля S 0≤P(A) ≤1 (9)
Для достоверного события A P(A)=1 (10)
Теорема сложения вероятностей для элементарных событий: P(A) – вероятность любого события A есть сумма вероятностей составляющих его элементарных событий: B и C.
P(A)=P(B)+(C) (11)
Дополнительные свойства:
Если
- дополнительное A
событие, то вероятность P(
)=1-P(A)
(12)Если A – достоверное событие, то - невозможное событие и P( )=0 (13)
Если событие
,
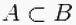то P(A)
≤P(B)
(14)
Аксиоматика Колмогорова.
Впервые, проблема аксиоматического построения теории вероятностей, как логически совершенной науки, была поставлена и решена теоретиком, исходившим из качественного сравнения случайных событий, но их большей или меньшей вероятности. Позднее, Колмогоровым (1929г.) был разработан другой подход, тесно связанный с метрической теорией функций и теорией множеств, и основанной на понятиях элементарного события и пространства (множества) «омега» элементарных событий. Отметим, что аксиоматический подход включает в себя классическое и статическое определение вероятностей, как частные случаи, и преодолевает недостаточность каждого из них.