Распределение Максвелла – Больцмана.

Это распределение получается из канонического, если воспользоваться выражением для гамильтониана :

.

Если проинтегрировать по ( по ), то эти распределения можно получить по - отдельности. Кроме того, это есть вероятность одной частице иметь координаты и скорости в заданном фазовом объеме (по координатам и импульсам остальных частицам мы проинтегрировали).

Задачи.

34. Получить распределение по модулю скорости, проекции и энергии для газа, не находящегося во внешнем поле.

Решение: Энергия газа не зависит от координат. Тогда интегрирование по координатам дает , который можно включить в нормировочный множитель (пока еще не определенный). Проинтегрировав по всем скоростям, кроме одной и включив эти интегралы в , мы получим функцию , описывающую распределение вероятностей скоростей для одной частицы:

.

найдем из условия нормировки: , откуда (интеграл Пуассона) . Чтобы получить распределение по одной компоненте скорости (скажем, ), необходимо проинтегрировать плотность по двум остальным проекциям скорости. В результате получим:

.

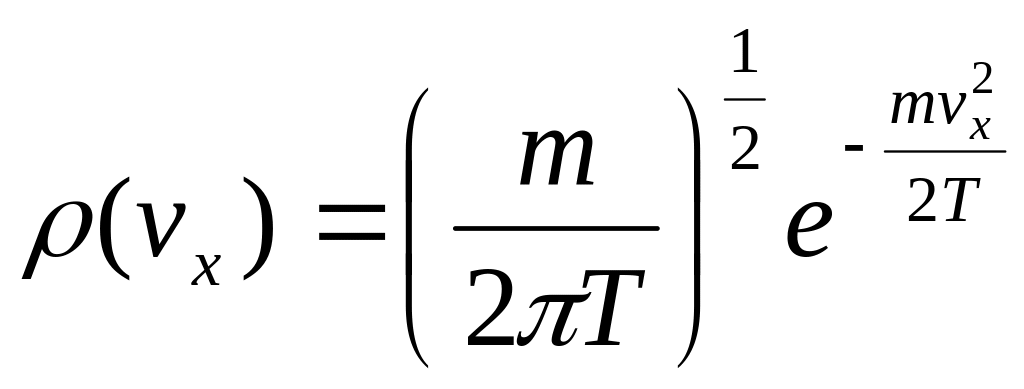Чтобы получить распределение по модулю скорости, запишем в виде:

,

и перейдем к сферическим координатам в пространстве скоростей:

, . Тогда:

(оно автоматически оказывается нормированным).

Наконец, чтобы получить распределение по энергии, подставим . В результате получим:

Используя эти распределения, по общим формулам, получим средние:

а)

(для четных ).

(напомним, что ).

В частности:

: .

Заметим, что (теорема о равномерном распределении энергии по степеням свободы).

.

Для нечетных (нечетная функция).

б) .

В частности:

Для , ( ),

а для , .

Наиболее вероятная по модулю скорость, получается дифференцированием

, по :

. Следовательно, при

в) .

В частности при а при .

Аналогично получается наиболее вероятное значение энергии

35. Найти вероятность того, что две частицы имеют абсолютные значения скорости относительного движения в интервале от до . Найти также .

Решение: Ввиду независимости движения частиц функция распределения распадается на произведение функций распределения каждой из частиц:

, где .

Перейдем от к новым переменным – относительной скорости и скорости центра масс :

, , следовательно , (якобиан перехода равен единице) и .

Далее нетрудно показать, что

,

где , а - приведенная масса .

Следовательно

Функция распределения по относительной скорости получается отсюда интегрированием по (обе функции распределения автоматически нормированы).

.

Среднее значение относительной скорости:

=

{если частицы одного сорта, то } = .

36. Н айти число соударений в единицу времени молекулы радиуса 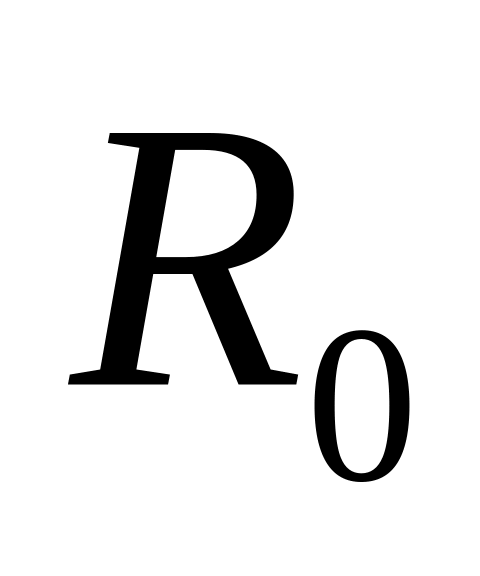и среднюю длину свободного пробега. Концентрация молекул .

Решение:

Если считать, что газ однородный, и зафиксировать все частицы кроме одной, то она будет двигаться по цилиндрической трубе со скоростью , пока не встретит «неподвижную» частицу. Тогда из элементарной пропорции находим: , (т. к. в цилиндре находится только одна частица). Очевидно:

,

где  - среднее время между столкновениями. Число столкновений в единицу времени:

.

Средняя длина пробега:

36. Запирающий потенциал, создающий электронным облаком вблизи поверхности . Определить плотность тока термоэлектронной эмиссии.

Решение:

Вклад в термоэлектронную эмиссию дают лишь те электроны, скорость которых подчиняется условию (ось перпендикулярна поверхности).

.

Вклад в термоэлектронный ток электронов, движущихся в интервале скоростей , определяется распределением Максвелла:

{ } =

.

Следовательно

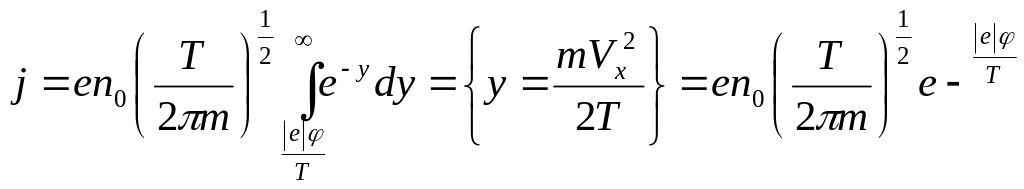
36. Найти центр масс столбом идеального газа в однородном поле тяжести, считая температуру неизменной.

Решение: Если проинтегрировать исходное распределение по всем скоростям, то получим распределение Больцмана:

,

определяющее вероятность координаты одной частицы (по координатам и импульсам остальных частиц мы также проинтегрировали). Остается еще проинтегрировать по и и все интегралы включить в . тогда, в случае однородного поля ( )

, .

Находим из условия нормировки: .

Положение центра масс находим по общей формуле:

, но - есть вероятность координаты ( ). Поэтому:

.

(здесь – масса одной молекулы)

NB , следовательно, в приближении изотермичности атмосферы получаем барометрическую формулу .

36. Смесь идеальных газов, состоящих из одинакового количества частиц с различными массами атомов, заключена в цилиндр высоты и помещена в поле тяжести Земли. Определить центр масс системы.

Решение: С учетом результата предыдущей задачи перепишем распределение в виде:

, .

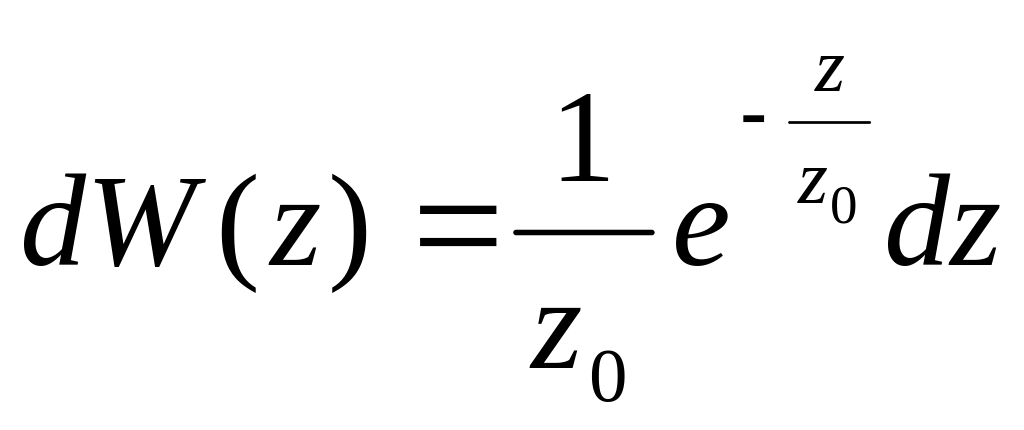Тогда центр тяжести одного сорта частиц:

.

Общий центр тяжести:

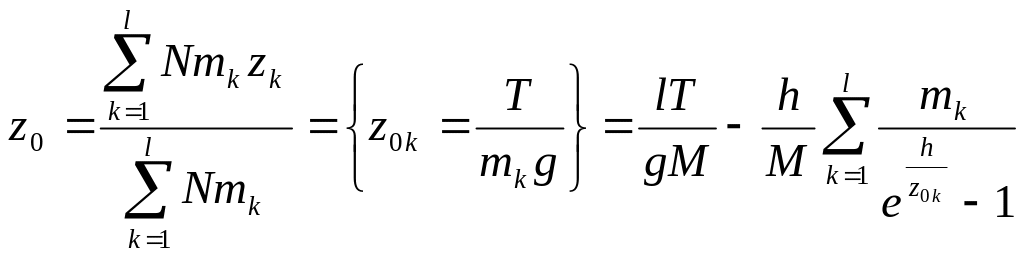
36. Вывести закон Дальтона для смеси N идеальных газов , где 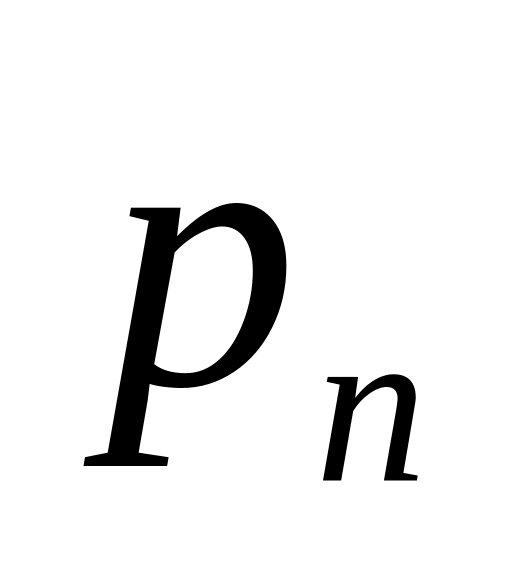– парциальное давление.

Решение: Гамильтониан смеси: .

Это означает, что зависимость от объема имеет следующий вид:

,

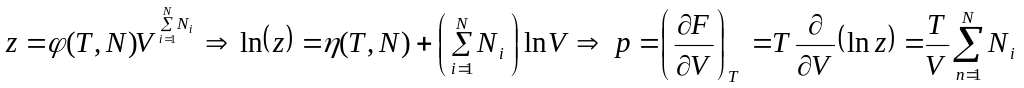но - парциальное давление и, следовательно

36. В тонкостенном сосуде, содержащем идеальный газ с концентрацией и средней скорости молекул , проделано небольшое круглое отверстие сечением . Определить число молекул, попадающих в единицу времени на круглый диск радиуса , находящийся на расстоянии от отверстия.

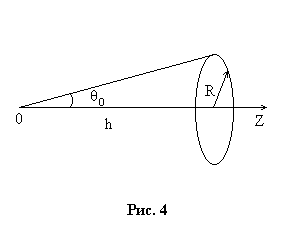
Решение: Число частиц, вылетающих в единицу времени из отверстия и движущихся поду углами в интервале (и, естественно попадающих на диск, см. рис. 4) к оси :

,

где - –компонента плотности потока таких молекул. Считая, что скорости молекул распределены по Максвеллу, получаем:

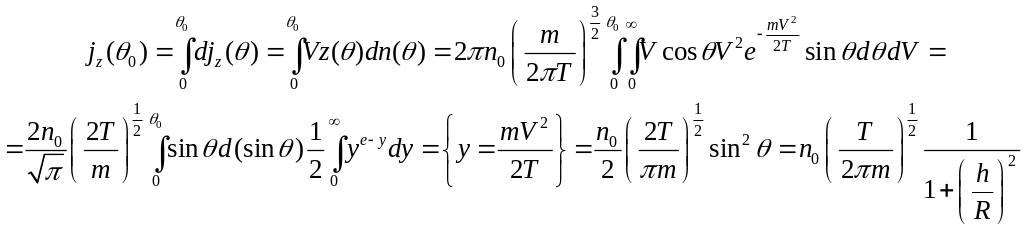
С учетом того, что средняя скорость молекул:

получаем .

NB При получаем скорость истечения газа из отверстия -.

41. Определить среднюю скорость молекул, выходящих из отверстия.

Решение: Воспользуемся распределением Максвелла. При этом нас будет интересовать только – проекция скорости. Число частиц, имеющих скорость в интервале :

. Следовательно, средняя скорость .