- •Розповсюдження та тиражування без офіційного дозволу заборонено
- •Структура залікового кредиту курсу для спеціальності 6.010102 – початкове навчання (3 р.Н.).
- •Робочий навчальний план з математики.
- •Питання до екзамену за і семестр
- •Питання до екзамену за ііі семестр
- •Основна література
- •Додаткова література
- •Методичні посібники
- •Модуль 1: «Множини. Відповідності. Відношення.». Змістовний модуль 1.1. «Множини та операції над ними». План.
- •Література
- •1. Поняття множини та її елементу, їхні позначення. Загальноприйняті позначення основних числових множин. Способи задання множин.
- •2. Порожня, скінченна, нескінченна та універсальна множини. Підмножина. Власні та невласні підмножини даної множини. Рівні та нерівні множини.
- •4. Операція об’єднання (додавання) множин та основні властивості (закони) цієї операції.
- •Малюнок № 1.7. Доведення переставного закону .
- •5. Операція перетину множин та основні властивості (закони) цієї операції.
- •Малюнок № 1.8. Перетин множин .
- •6. Операції різниці (віднімання) множин та основні властивості (закони) цієї операції.
- •7. Операція доповнення до даної та універсальної множини та основні властивості (закони) цих операцій.
- •Малюнок № 1.18. Доведення закону де Моргана ()'''.
- •8. Поняття розбиття множини на класи (підмножини), що попарно не перетинаються. Розбиття множини на класи за допомогою однієї, двох і трьох властивостей. Класифікації.
- •9. Поняття кортежу та впорядкованої пари. Поняття кортежу довжини n. Рівні пари та кортежі.
- •Малюнок № 1.19. Задання декартового добутку множин за допомогою графа.
- •Модуль 1: «Множини. Відповідності Відношення.». Змістовний модуль1.2. «Відповідності та відношення.». План.
- •Малюнок № 1.20. Граф відповідності.
- •4. Відношення еквівалентності та порядку, їх властивості. Впорядковані множини. Зв'язок відношення еквівалентності з розбиттям множини на класи, що попарно не перетинаються.
- •Розв’язання:
- •Розв’язання:
- •Малюнок № 1.21. Розв’язання задачі 2.
- •Розв’язання:
- •2. Розміщення з повтореннями та без повторень.
- •Доведення:
- •Розв’язання.
- •Доведення.
- •Розв’язання.
- •3. Перестановки з повтореннями та без повторення.
- •Розв’язання.
- •Доведення.
- •Розв’язання.
- •4. Комбiнацiї та їх властивості.
- •Доведення.
- •Розв’язання.
- •Доведення.
- •Доведення.
- •Запитання для самоконтролю та завдання для самостійної роботи студентів за модулем 1.
- •Модуль 2: «Висловлення. Предикати. Теореми.». Змістовний модуль 2.1. «Поняття.».
- •1. Поняття як форма мислення, зміст і обсяг поняття та зв'язок між ними.
- •Діаграма № 2.1. Відношення часткового збігу між поняттями.
- •Діаграма № 2.2. Відношення підпорядкування між поняттями.
- •3. Аксіоми. Теореми. Ознаки.
- •Означуване поняття
- •Видова відмінність
- •Модуль 2: «Висловлення. Предикати. Теореми.». Змістовний модуль 2.2. «Висловлення та предикати.».
- •1. Поняття висловлення, їх види (елементарні, складені, рівносильні) та позначення.
- •2. Поняття предиката, його позначення та область визначення. Поняття кванторів існування та загальності, їх позначення та зв'язок між ними.
- •3. Операція заперечення над висловленнями та предикатами. Таблиці істинності. Основні властивості (закони) операції заперечення.
- •Діаграма № 2.3. Множина істинності та заперечення даного предиката ā(х).
- •4. Операція кон’юнкції над висловленнями та предикатами. Її таблиця істинності. Основні властивості (закони) операції кон’юнкції.
- •4.1. Операція кон'юнкції висловлень.
- •4.2. Операція кон'юнкції предикатів.
- •5. Операція диз’юнкції над висловленнями та предикатами. Її таблиця істинності. Основні властивості (закони) операції диз’юнкції.
- •5.1. Операція диз’юнкції над висловленнями.
- •5.2. Диз'юнкція двох предикатів.
- •6. Операція імплікації над висловленнями та предикатами. Її таблиця істинності. Основні властивості (закони) операції імплікації.
- •6.1. Операція імплікації висловлень.
- •6.2. Операція імплікації предикатів.
- •7. Операція еквіваленції над висловленнями та предикатами. Її таблиця істинності. Основні властивості (закони) операції еквіваленції.
- •7.1. Операція еквіваленції висловлень.
- •7.2. Операція еквіваленції предикатів.
- •Діаграма № 2.7. Множина істинності еквіваленції предикатів.
- •Розв’язування:
- •Розв’язання:
- •Запитання для самоконтролю та самостійної роботи студентів за змістовним модулем 2.2.
- •Модуль 2: «Висловлення. Предикати. Теореми.». Змістовний модуль 2.3. «Теореми.». План.
- •1. Поняття теореми, її будова. Види теорем (дана, обернена, протилежна, обернена до протилежної, спряжені теореми) та зв'язок між ними.
- •2. Способи доведення теорем (дедуктивний, індуктивний, метод від супротивного тощо).
- •Доведення:
- •3. Необхідні та достатні умови.
- •4. Поняття міркування, правильні та неправильні міркування. Перевірка правильності міркувань з допомогою кругів л.Ейлера.
- •1. Короткі історичні відомості про виникнення понять натурального числа і нуля.
- •1. Питання № 1 вивчається самостійно за таким планом:
- •2. Різні підходи до побудови теорії цілих невід’ємних чисел.
- •Діаграма № 3.1. Співвідношення між числовими множинами.
- •3. Поняття натурального числа і нуля у теоретико-множинній (кількісній) теорії.
- •Малюнок № 3.1.
- •5. Множина цілих невід’ємних чисел та її властивості.
- •6. Визначення суми на множині цілих невід’ємних чисел, її існування та єдиність. Операція додавання та її основні властивості (закони).
- •Доведення:
- •Доведення:
- •7. Віднімання цілих невід’ємних чисел, зв'язок віднімання з додаванням. Теореми про існування та єдиність різниці.
- •Доведення:
- •Доведення:
- •8. Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
- •Доведення:
- •Доведення:
- •Доведення:
- •Доведення:
- •10. Операція ділення з остачею на множині цілих невід’ємних чисел.
- •Доведення:
- •Завдання для самоконтролю та самостійної роботи студентів за змістовним модулем 3.1.
- •Модуль ііі. «різні підходи до побудови арифметики цілих невідємних чисел». Змістовний модуль 3.2. «Аксіоматична побудова арифметики цілих невід’ємних чисел.». План
- •1. Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
- •2. Властивості аксіоматики (несуперечливість, повнота, незалежність) цілих невід’ємних чисел. Система аксіом Дж.Пеано. Поняття натурального числа і нуля в аксіоматичній теорії.
- •3. Метод математичної індукції.
- •Доведення:
- •Доведення:
- •4. Аксіоматичне означення додавання цілих невід’ємних чисел в аксіоматичній теорії. Таблиці і закони додавання.
- •Доведення:
- •Доведення:
- •5. Аксіоматичне означення множення цілих невід’ємних чисел в аксіоматичній теорії. Таблиці і закони множення.
- •6. Відношення порядку на множині цілих невід’ємних чисел.
- •7. Означення віднімання і ділення цілих невід’ємних чисел в аксіоматичній теорії.
- •Модуль ііі. «різні підходи до побудови арифметики цілих невідємних чисел». Змістовний модуль 3.3. «Натуральне число як результат вимірювання величини.». План.
- •1. Поняття натурального ряду чисел та його відрізка. Лічба елементів скінченої множини. Порядкові і кількісні натуральні числа.
- •2. Порівняння відрізків, дії над відрізками. Натуральне число як результат вимірювання величини. Натуральне число як міра величини. Натуральне число як міра відрізка.
- •Малюнок № 3.6. Різниця а-b відрізків.
- •3. Означення операцій додавання і віднімання чисел, що розглядаються як міри відрізків. Трактування множення і ділення, які розглядаються як міри відрізків.
- •Модуль іу. «системи числення. Подільність чисел.». Змістовний модуль 4.1. «Системи числення.». План.
- •1. Позиційні та непозиційні системи числення, запис чисел у позиційних і непозиційних системах числення.
- •2. Алгоритми арифметичних операцій над цілими невід’ємними числами у десятковій системі числення.
- •Розв’язання:
- •Розв’язання:
- •Розв’язання:
- •Модуль іу. «системи числення. Подільність чисел.». Змістовний модуль 4.2. «Подільність цілих невід’ємних чисел.». План.
- •1. Поняття «відношення подільності» та його властивості.
- •2. Теореми про подільність суми, різниці і добутку цілих невід’ємних чисел на натуральні числа.
- •3. Загальна ознака подільності б.Паскаля. Ознаки подільності цілих невід’ємних чисел на 2, 3, 4, 5, 9, 25.
- •4. Прості і складені числа. Нескінченність множини простих чисел. Решето Ератосфена.
- •5. Основна теорема арифметики цілих невід’ємних чисел.
- •Розв’язання:
- •6. Дільники і кратні. Спільні дільники і спільні кратні. Найбільший спільний дільник (нсд) і найменше спільне кратне (нск), їх властивості.
- •7. Обчислення нсд і нск способом канонічного розкладу на прості множники та за алгоритмом Евкліда.
- •Розв’язання:
- •8. Ознаки подільності на складені числа.
- •Завдання для самоконтролю та самостійної роботи студентів.
- •Модуль у. «розширення поняття про число». Змістовний модуль 5.1. «Цілі числа.». План.
- •1. Задача розширення поняття про число. Необхідність розширення множини натуральних чисел.
- •2. Побудова множини цілих чисел. Зображення цілих чисел на числовій прямій.
- •Малюнок № 5.1. Зображення точок а(4) і в(-6).
- •Розв’язання:
- •3. Властивості множини цілих чисел.
- •Доведення:
- •4. Додавання, віднімання, множення і ділення цілих чисел. Теореми про існування та єдиність цих операцій. Закони операцій додавання і множення.
- •Модуль у. «розширення поняття про число». Змістовний модуль 5.2. «Раціональні числа.». План.
- •1. Необхідність розширення множини цілих чисел.
- •2. Поняття дробу. Рівність дробів. Основна властивість дробів. Скорочення дробів та їх зведення до спільного знаменника. Нескоротні дроби.
- •Доведення.
- •3. Невід’ємні раціональні числа та їх властивості.
- •Доведення.
- •Доведення.
- •4. Відношення порядку на множині невід’ємних раціональних чисел.
- •Доведення.
- •Доведення.
- •5. Додавання і віднімання невід’ємних раціональних чисел. Теореми про існування та єдиність суми і різниці. Властивості (закони) додавання.
- •Доведення.
- •Доведення.
- •Доведення.
- •6. Множення і ділення невід’ємних раціональних чисел. Теореми про існування та єдиність добутку та частки. Властивості (закони) множення.
- •Доведення.
- •Доведення.
- •Доведення.
- •7. Властивості множини невід’ємних раціональних чисел.
- •8. Десяткові дроби, їх порівняння, операції над ними. Перетворення десяткових дробів у звичайні та звичайних у десяткові.
- •Доведення.
- •9. Додатні раціональні числа як нескінченні періодичні десяткові дроби. Чисті та мішані періодичні дроби та їх перетворення у звичайні.
- •Розв’язання.
- •10. Множина раціональних чисел, модуль раціонального числа, операції над раціональними числами. Властивості множини раціональних чисел.
- •Діаграма № 5.1. Співвідношення між числовими множинами q, z, n.
- •Доведення.
- •Малюнок № 5.2.
- •2. Додатні ірраціональні числа. Невід’ємні дійсні числа.
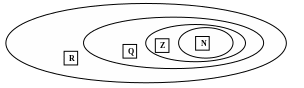
- •Діаграма № 5.2. Співвідношення між числовими множинами n, z, q, r.
- •3. Відношення порядку на множині дійсних чисел.
- •Розв’язання.
- •Розв’язання.
- •4. Додавання і віднімання додатних дійсних чисел.
- •Розв’язання.
- •Розв’язання.
- •Розв’язання.
- •5. Множення та ділення додатних дійсних чисел.
- •Розв’язання.
- •Розв’язання.
- •6. Множина дійсних чисел та її властивості.
- •Запитання для самоконтролю та самостійної роботи студентів за модулем у.
- •Модуль 6. : «вирази. Рівняння. Нерівності. Функції». Змістовний модуль 6.1. «Вирази.».
- •1. Числові вирази та їх види. Значення числового виразу та порядок обчислення значень числового виразу.
- •Розв’язання:
- •2. Числові рівності та нерівності, їх властивості.
- •3. Вираз із змінною та його область визначення.
- •4. Тотожні перетворення виразів. Тотожності. Виведення основних тотожностей.
- •Модуль 6. : «вирази. Рівняння. Нерівності. Функції». Змістовний модуль 6.2. «Рівняння, їх системи і сукупності.».
- •Розв’язання:
- •2. Рівносильні рівняння. Теореми про рівносильність рівнянь.
- •Розв’язання:
- •Доведення:
- •Розв’язання:
- •3. Рівняння з двома змінними. Рівняння лінії. Рівняння прямої та їх види.
- •Малюнок № 6.1. Графік рівняння кола.
- •Малюнок № 6.3.
- •Малюнок № 6.4.
- •4. Системи та сукупності рівнянь з двома змінними та способи (алгебраїчні та графічні) їх розв’язування.
- •Розв’язання.
- •Розв’язання.
- •Розв’язання.
- •5. Застосування рівнянь та їх систем до розв’язування текстових задач.
- •Модуль 6. : «вирази. Рівняння. Нерівності. Функції». Змістовний модуль 6.3. «Нерівності, їх системи і сукупності.».
- •2. Рівносильні нерівності. Теореми про рівносильність нерівностей.
- •Доведення.
- •Доведення.
- •3. Системи та сукупності нерівностей з однією змінною та способи їх розв’язування. Нерівності та системи нерівностей з двома змінними, графічний спосіб їх розв’язування.
- •Розв’язання.
- •Модуль 6. : «вирази. Рівняння. Нерівності. Функції». Змістовний модуль 6.4. «Функції.».
- •1. Поняття числової функції, способи їх задання, графік та властивості.
- •2. Пряма пропорційність, її властивості та графік.
- •3. Лінійна функція, її властивості та графік.
- •4. Обернена пропорційність, її властивості та графік.
- •5*. Квадратична функція, її властивості та графік.
- •6*. Операції над функціями та графіками, перетворення графіків.
- •Розв’язання.
- •Розв’язання.
- •Розв’язання.
- •Розв’язання.
- •Запитання для самоконтролю та самостійної роботи студентів.
- •Модуль 7: «елементи геометрії. Величини.». Змістовний модуль 7.1. «Геометричні побудови на площині.».
- •1. Короткі історичні відомості про виникнення та розвиток геометрії. Поняття про аксіоматичний метод побудови геометрії та історію його розвитку в геометрії.
- •2. Основні геометричні побудови циркулем і лінійкою.
- •Побудова кута, що дорівнює даному (див. Малюнок № 7.1.).
- •Поділ відрізка пополам.
- •Малюнок № 7.2. Поділ кута пополам.
- •Побудова прямої, яка проходить через дану на ній точку, перпендикулярно до даної прямої (малюнок № 7.4.).
- •Побудова трикутника за трьома сторонами.
- •3. Основні методи геометричних побудов (метод гмт, методи осьової та центральної симетрії, метод паралельного перенесення, метод гомотетії, алгебраїчний метод).
- •Метод геометричних місць точок.
- •Малюнок № 7.5. Метод симетрії відносно прямої.
- •Метод повороту площини навколо точки.
- •Метод симетрії відносно даної точки.
- •Метод паралельного перенесення.
- •Метод гомотетії.
- •Алгебраїчний метод.
- •4. Побудова правильних многогранників.
- •2. Правильні многогранники та їх види.
- •Доведення:
- •3. Поняття тіла обертання, їх види (циліндр, конус, куля. Сфера) та їх зображення на площині.
- •Модуль 7: «елементи геометрії. Величини.». Змістовний модуль 7.3. «Величини та їх вимірювання.».
- •1. Поняття величини та її вимірювання. Відображення властивостей реального світу через поняття величини. Види величин.
- •2. Поняття довжини відрізка та способів його вимірювання. Основні властивості довжини. Одиниці вимірювання довжини та співвідношення між ними.
- •3. Поняття площі плоскої фігури, її основні властивості та способи вимірювання. Рівновеликі та рівноскладені фігури. Одиниці вимірювання площі та співвідношення між ними.
- •Малюнок № 7.10.. Квадрати нульового рангу.
- •Малюнок № 7.11. Фігури ф і f.
- •Доведення:
- •4. Виведення формул для знаходження площі паралелограма, трикутника, трапеції. Формули для знаходження площ поверхонь просторових геометричних фігур.
- •Малюнок № 7.12.
- •Малюнок № 7.13.
- •Доведення:
- •Малюнок № 7.14.
- •Доведення:
- •Доведення:
- •Малюнок № 7.16.
- •5*. Поняття об’єму тіла, його властивостей, способів його вимірювання, одиниць вимірювання та співвідношень між ними. Об’єми многогранників та тіл обертання.
- •Запитання для самоконтролю та самостійної роботи студентів.
Доведення.
Для доведення теореми розглянемо квадрат, довжина сторони якого складає 1 одиницю (див. малюнок № 5.2.).
За умовою АВ=1,
ВС=1. Припустимо,
що довжина діагоналі АС
дорівнює нескоротному дробу
,
тобто раціональному числу. За теоремою
Піфагора із трикутника АВС
маємо: АС2=АВ2+ВС2![]() .
Тоді (
)2=2.
Отже, p2=2q2.
Права частина останньої рівності
ділиться націло на 2, а тому і ліва частина
p2
2.
Це означає, що число p
– парне, тобто p=2p1.
Таким чином, 4p12=2q2.
Звідси, 2p12=q2,
тобто число q
– парне і q=2q1.
Отже,
.
Тоді (
)2=2.
Отже, p2=2q2.
Права частина останньої рівності
ділиться націло на 2, а тому і ліва частина
p2
2.
Це означає, що число p
– парне, тобто p=2p1.
Таким чином, 4p12=2q2.
Звідси, 2p12=q2,
тобто число q
– парне і q=2q1.
Отже,
![]() тобто
дріб
-
скоротний, а це суперечить умові. Ця
суперечність говорить про те, що наше
припущення про раціональність числа
було хибним. Таким чином, якщо довжини
сторін квадрата виражаються раціональними
числами, то довжина його діагоналі не
виражається раціональним числом. Отже,
діагональ квадрата несумірна з його
стороною. Теорему доведено.
тобто
дріб
-
скоротний, а це суперечить умові. Ця
суперечність говорить про те, що наше
припущення про раціональність числа
було хибним. Таким чином, якщо довжини
сторін квадрата виражаються раціональними
числами, то довжина його діагоналі не
виражається раціональним числом. Отже,
діагональ квадрата несумірна з його
стороною. Теорему доведено.
В С



А Д
Малюнок № 5.2.
Із доведеної
теореми випливає, що, по-перше, існують
відрізки, довжина яких не виражається
раціональним числом, по-друге, не існує
раціонального числа, квадрат якого
дорівнює 2, тобто рівняння х2=2
в множині раціональних чисел немає
розв'язку.
Отже виникає потреба в розширенні
множини раціональних чисел, причому
повинні виконуватися наступні вимоги:
1) довжина будь-якого відрізка повинна
виражатися цим числом; 2) у новій числовій
множині завжди повинно мати розв'язок
рівняння виду хn=а,
де а![]() 0;
3) множина раціональних чисел повинна
входити в нову числову множину.
0;
3) множина раціональних чисел повинна
входити в нову числову множину.
2. Додатні ірраціональні числа. Невід’ємні дійсні числа.
2. Ми вже розглянули звичайні та десяткові дроби та виявили, що між ними існує певний зв'язок, а саме: кожний десятковий дріб можна перетворити у звичайний; не кожний звичайний дріб можна перетворити у скінченний десятковий дріб (коли це не можна зробити?!). Як скінченні, так і нескінченні періодичні десяткові дроби належать до множини Q раціональних чисел, яку можна також називати множиною періодичних десяткових дробів. З іншого боку, розглядаючи процес вимірювання величин чи розв’язування рівнянь виду х²=а, ми отримуємо числа, які не є періодичними десятковими дробами. У вказаних випадках можуть з’являтися нескінченні неперіодичні десяткові дроби, наприклад: 0,10100100010000…, √2, √3,√5, π, е тощо. Отже, такі дроби ми можемо отримати при вимірюванні несумірних відрізків і при розв'язанні рівнянь виду х2к=а, де а 0. Виявляється, що нескінченні неперіодичні десяткові дроби зображують числа, які не належать до множини раціональних чисел. Це числа нової природи. Таким чином, постає питання розширення множини раціональних чисел, яке слід провести, дотримуючись наступних умов:
до множини раціональних чисел приєднаємо числа нової природи – ірраціональні числа;
визначимо арифметичні операції додавання, віднімання, множення і ділення над ірраціональними числами так, щоб вони не суперечили правилам виконання дій над раціональними числами;
поширимо основні закони (властивості) дій над раціональними числами на числа нової природи;
поставимо завдання про можливість знаходження розв’язків рівняння виду хn=а, де n і a - будь-які натуральні числа;
поставимо вимогу про можливість знаходження спільної міри для будь-яких однорідних величин.
Для виконання поставлених завдань введемо означення понять, які відносяться до нової числової множини.
Означення: нескінченний неперіодичний десятковий дріб називається ірраціональним числом.
Прикладом таких чисел є наступні: Наприклад: 2,3, =3,141592…, 2,212212221… тощо. Хоча в означенні нічого не говориться про існування таких чисел, але, доводячи теорему про несумірність сторони квадрата з його діагоналлю, ми фактично довели теорему про існування ірраціональних чисел. Якщо до множини невід’ємних раціональних чисел ми приєднаємо додатні ірраціональні числа, то отримаємо множину невід’ємних дійсних чисел, яку прийнято позначати R0. якщо ж розглянути ще й від’ємні ірраціональні числа, то матимемо справу з множиною дійсних чисел.
Означення: об'єднання множини Q раціональних чисел з множиною додатних і від'ємних ірраціональних чисел називають множиною дійсних чисел.
Множину дійсних чисел прийнято позначати R. Таким чином, можна записати таке співвідношення між відомими нам числовими множинами: RQZN або NZQR, яке можна зобразити за допомогою кругів Ейлера так, як це зроблено на діаграмі № 5.2.