
Задание №1
Условие: Ателье по ремонту аппаратуры имеет 5 опытных мастеров одной квалификации. В среднем в течение часа от населения поступает в ремонт λ=1,8 аппаратов в час. Входной поток заявок простейший. Среднее время ремонта одного аппарата одним мастером 2,3 часа (tобс.). Время обслуживания показательное. Очередь не ограничена.
Задание:
1. Описать состояния системы, построить грай состояний.
2. Найти вероятности системы для стационарного случая и показатели
эффективности работы ателье, проанализировать результаты расчетов, оценить работу ателье.
3.
Найти функциональную зависимость
средней длины очереди от интенсивности
входного потока
![]() и от времени обслуживания
и от времени обслуживания
![]() .Представить
зависимость в виде таблиц и графиков.
.Представить
зависимость в виде таблиц и графиков.
4. Вычислить процент аппаратов, отремонтированных без очереди, а также вероятность того, что все мастера будут заняты в тот момент, когда придет следующая заявка.
5. Найти оптимальное число мастеров в ателье, используя стоимостную функцию:
![]()
Известно, что с1=500 уе – стоимость дополнительного мастера в ателье, с2=50 уе – потери от простоя аппарата в ожидании ремонта, с3=100уе – потери от простоя одного мастера.
6. Если интенсивность потока аппаратов, отданных в ремонт, увеличится в 1.5 раз, сколько мастеров потребуется ателье за это время?
Теоретическое введение.
Данная СМО – многоканальная система с неограниченной очередью.
Рассмотрим общий случай, найдем вероятности стационарных состояний СМО, оценим работу СМО.
Запишем состояния системы СМО:
S0– все каналы свободны,
S1 – один канал занят.
S2 – два канала заняты.
…………..
Sn – n каналов заняты.
Sn+1 - n каналов заняты, одна заявка в очереди.
Sn+2 – n каналов заняты, две заявки в очереди.
и так далее.
В этой СМО ни одна заявка не получит отказ: pотк=0
Граф СМО имеет вид:
nµ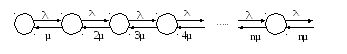



![]()
Рис. 1
Интенсивности переходов Si в Si+1, при i=0, 1,…n-1 одинаковы и равны λ, так как входной поток простейший.
Интенсивность обратных переходов является кратной числу занятых каналов.
Запишем алгебраические уравнения для стационарного случая и определим из них и нормировочного условия p0.
![]()
Обозначим λ/µ=ρ, рассмотрим величину ρ/n. Если ρ/n<1, то вероятности стационарных состояний можно найти по формулам:
![]() (1)
(1)
![]() ;
;![]() ;…;
;…;![]() ;
;![]() ;…;
;…;![]() .
.
Если ρ/n≥1, то предельные вероятности также, как стационарные вероятности, не существуют, очередь растет неограниченно и СМО не может работать. Запишем формулы для расчета коэффициентов эффективности работы СМО для случая ρ/n<1.
pотк=0, Q=1- pотк=1, A=λ (2)
Среднее число занятых каналов –
![]() (3)
(3)
Среднее число заявок в очереди –
 (4)
(4)
Среднее время ожидание
![]() (5)
(5)
Вероятность того, что все каналы заняты(событие А), вычисляется по формуле:
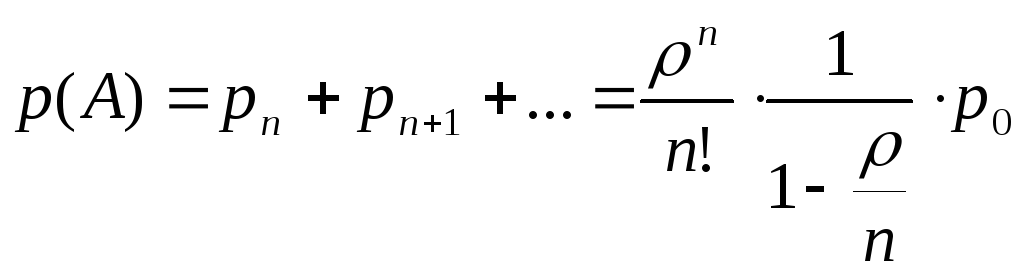 (6)
(6)
Соответственно, вероятность того, что хотя бы один канал свободен, вычисляется по формуле обратной вероятности:
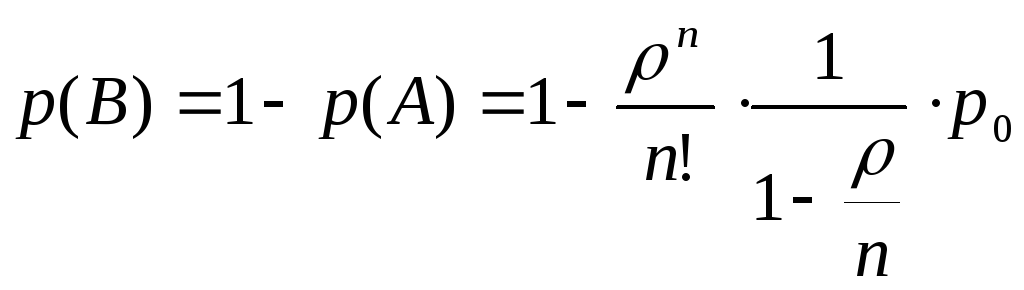 (7)
(7)
Чтобы найти оптимальное количество обслуживающих каналов для СМО с неограниченной очередью, используется стоимостная функция c(n), где n – число обслуживающих каналов. Ниже представлены виды стоимостных функций:
1.
![]() ,где
n
– число обслуживающих каналов, с1 –
затраты на работу одного дополнительного
канала в единицу времени, с2 – цена
ожидания в единицу времени в расчете
на одно требование, zсист(n)
– среднее число клиентов в СМО для
каждого n.
,где
n
– число обслуживающих каналов, с1 –
затраты на работу одного дополнительного
канала в единицу времени, с2 – цена
ожидания в единицу времени в расчете
на одно требование, zсист(n)
– среднее число клиентов в СМО для
каждого n.
2.
![]() ,
где n
– число обслуживающих каналов, с1 –
затраты на работу одного дополнительного
канала, к единице времени, с2 – цена
ожидания одной заявки в единицу времени,
с3 – стоимостные потери от простоя
одного канала в единицу времени, r0(n)
– среднее число заявок, стоящих в
очереди, ксв(n)
– среднее число свободных каналов.
,
где n
– число обслуживающих каналов, с1 –
затраты на работу одного дополнительного
канала, к единице времени, с2 – цена
ожидания одной заявки в единицу времени,
с3 – стоимостные потери от простоя
одного канала в единицу времени, r0(n)
– среднее число заявок, стоящих в
очереди, ксв(n)
– среднее число свободных каналов.
3.
![]() ,где
с1 – стоимостные потери из-за простоя
одного клиента в СМО, t1(n)
– среднее время простоя одного клиента
в СМО,
,где
с1 – стоимостные потери из-за простоя
одного клиента в СМО, t1(n)
– среднее время простоя одного клиента
в СМО,
с2 – стоимость одного часа простоя канала СМО, t2(n) – среднее время простоя канала.
Оптимальным будет считаться то число каналов, при котором значение стоимостной функции будет минимальным.
Решение:
1. Запишем состояния системы СМО:
S0 – все мастера свободны,
S1 – один мастер занят.
S2 – два мастера заняты.
S3 – три мастера заняты.
S4 – четыре мастера заняты.
S5 – все мастера заняты.
S6 – все мастера заняты, один аппарат в очереди.
S7 – все мастера заняты, два аппарата в очереди
и так далее.
Теоретически число состояний не ограничено(бесконечно).
Граф СМО имеет вид:
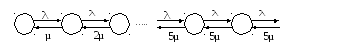
2. Вычислим стационарные вероятности состояний СМО:
![]()
![]()
![]()
![]()
![]() n=5
n=5 ![]()
По формуле (1) найдем начальную вероятность:
![]()
![]()
![]()
![]()
![]()
Заметим, что вероятность того, что все мастера свободны, очень мала:
p0=0.01
По формуле (2), относительная и абсолютная пропускные способности
равны:
pотк=0, Q=1- pотк=1, A=λ=1,8
По формуле (3) найдем среднее число занятых каналов:
![]()
Можно сделать вид, что ателье довольно сильно загружено.
Найдем среднее число аппаратов, ожидающих ремонт по формуле (4), и время ожидания (5):
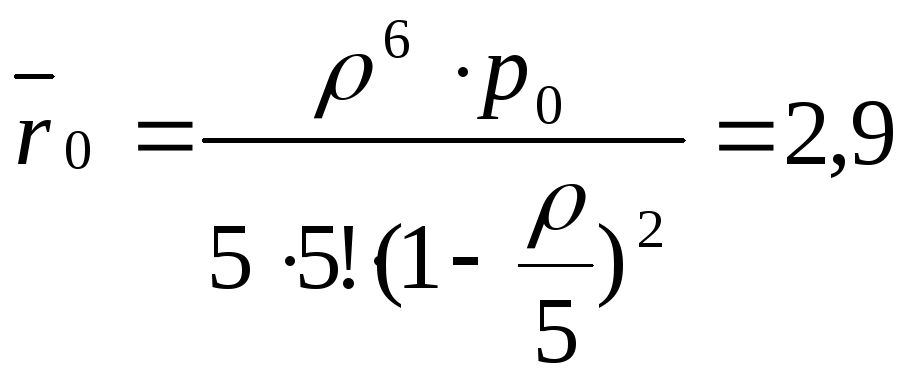
![]()
3.
Найдем функциональную зависимость
![]() ,
придавая λ различные значения из
диапазона 1,2…2,15. При λ, примерно равной
2, очередь начинает быстро возрастать,
и при λ=2,175 ρ=1, СМО перестает работать.
,
придавая λ различные значения из
диапазона 1,2…2,15. При λ, примерно равной
2, очередь начинает быстро возрастать,
и при λ=2,175 ρ=1, СМО перестает работать.
Зависимость представим в виде таблицы:
|
λ |
1,2 |
1,5 |
1,8 |
2,1 |
2,15 |
|
r0 |
0,22 |
0,803 |
2,92 |
25,62 |
83,533 |
Ниже представлен график зависимости.
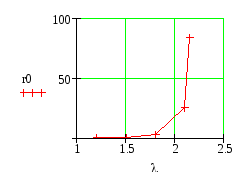
Если
один из мастеров заболеет или уйдет в
отпуск, то при tобсл=2.3,
ателье не сможет стационарно работать,
очередь будет расти неограниченно.
Зависимость
![]() представлена ниже.
представлена ниже.
|
tобсл |
2,3 |
2 |
1,5 |
1 |
|
r0 |
2,92 |
1,05 |
0,209 |
0,023 |
Ниже представлен график зависимости:
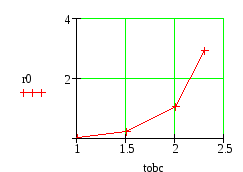
4.Найдем вероятность, что аппарат будет обслужен без очереди по формуле (7):
p(B)=1-p(A), где р(А) – вероятность того, что все мастера заняты.
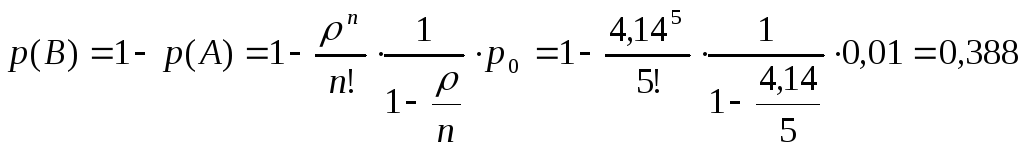
Аппарат будет обслужен без очереди в 39% случаев.
Вероятность того, что все мастера заняты (6) будет равна:
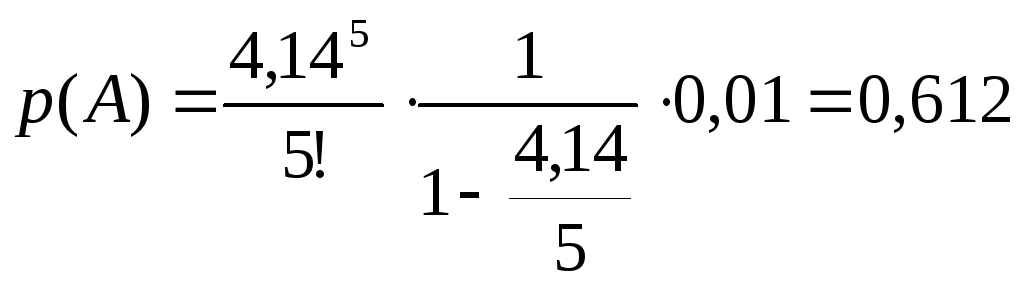
Значит, в 61% случаев все мастера будут заняты.
5. Найдем оптимальное число мастеров, если с1=500 уе – стоимость дополнительного мастера, с2=50 уе - потери от простоя аппарата в ожидании ремонта, с3 = 100 уе потери от простоя одного мастера.
Рассчитаем стоимостной показатель по формуле:
![]() .
.
При n=1..5 СМО не работает (ρ/n>1).
|
n |
5 |
6 |
7 |
8 |
9 |
|
c(n) |
2732,66 |
3221,7 |
3797,26 |
4389,7 |
4987,2 |
Наименьшее значение стоимостной функции достигается при n=5. Оптимальное число мастеров – пять.
5. Летом интенсивность пассажиров увеличивается в 1.5 раз (λ=2,7).
ρ=2,7*2,3=6,24, ρ/4>1. СМО не работает.
Определение оптимального числа кассовых аппаратов:
При n<7, ρ/n>1 СМО не работает.
Рассчитаем стоимостной показатель по формуле:
![]()
|
n |
7 |
8 |
9 |
10 |
|
c(n) |
3849,1 |
4176,7 |
4802,48 |
5389 |
Анализ работы: при n<7, СМО работать не будет, а оптимальное число аппаратов при λ=6,21 будет равно семи.
