4.6.2. Однородное линейное уравнение n-го порядка

Определение 4. Функция

z(x)=u(x)+iv(x), (4.6.10)

где u(x) и v(x) – вещественные функции от вещественной переменной x, а i= , называется комплексной функцией от вещественной переменной x.

Функции u(x) и v(x) называются соответственно вещественной и мнимой частями комплексной функции z(x). Примером такой функции является

e^ix=cos x+isin x, (4.6.11)

или функция более общего вида e^x, где =a+ib, причем a и b – вещественные:

e^x = e^(a+ib)x = e^axe^ibx = e^ax(cos bx+isin bx) = e^axcosbx+ie^axsinbx, (4.6.12)

Производная n-го порядка от функции z(x) no вещественной переменной x, в предположении, что u⁽ⁿ⁾(x) и v⁽ⁿ⁾(x) существуют, определяется так:

z⁽ⁿ⁾(x)=u⁽ⁿ⁾(x)+iv⁽ⁿ⁾(x), (4.6.13)

Опеределение 5. Комплексная функция от вещественной переменной x

y(x)=y₁(x)+iy₂(x) (4.6.14)

называется комплексным решением однородного линейного уравнения (4.6.2) в интервале (a, b), если подстановка ее в уравнение (4.6.2) обращает это уравнение в тождество, т. е. если

L[y(x)]  0 (a<x<b). (4.6.15)

Можно доказать, что всякое комплексное решение уравнения (4.6.2) порождает два вещественных решения этого уравнения, а именно: если комплексная функция y(x) является решением уравнения (4.6.2), то ее вещественная и мнимая части являются вещественными решениями этого уравнения.

Установим теперь три замечательных свойства решений однородного линейного уравнения.

1. Если y₁ есть решение однородного линейного уравнения (4.6.2), т.е.

L[y₁]  0, (4.6.16)

то функция

y=Cy₁, (4.6.17)

где C – произвольная постоянная, тоже является решением этого уравнения.

2. Если y₁ и y₂ – решения уравнения (4.6.2), то их сумма

y= y₁ + y₂ (4.6.18)

тоже является решением уравнения (4.6.2).

3. Если y₁,y₂,…y_m – решения уравнения (4.6.2), то их линейная комбинация

y=C₁y₁+C₂y₂+…+C_my_m, (4.6.19)

где C₁,C₂,...,C_m – произвольные постоянные, тоже является решением уравнения (4.6.2). Это свойство следует из 1 и 2.

Поставим теперь основной вопрос: каковы должны быть n частных решений y₁,y₂,…y_n, чтобы формула

y=C₁y₁+C₂y₂+…+C_ny_n, (4.6.20)

содержащая n произвольных постоянных C₁,C₂,...,C_n давала общее решение уравнения (4.6.2)? Чтобы ответить на этот вопрос, введем понятие о линейной независимости функций.

Определение 6. Функции y₁,y₂,…y_n называются линейно независимыми в интервале (a, b), если между ними не существует соотношения вида

₁y₁+₂y₂+…+_ny_n0 при a<x<b, (4.6.21)

где ₁,₂,…,_n – постоянные числа, не равные нулю одновременно. В противном случае функции y₁,y₂,…y_n называются линейно зависимыми в интервале (a, b).

Для случая двух функций y₁ и y₂ понятие линейной независимости в интервале (a, b) сводится, очевидно, к тому, чтобы отношение этих функций не было постоянным в интервале (a, b).

Пример 1. Функции y₁=1, y₂=x, …,y_n=x^n1 линейно независимы в интервале (,) и вообще в любом онтервале.

Действительно, соотношение

₁+₂x+…+_nx^n1=0,

в котором не все  равны нулю, не может выполняться тождественно, ибо оно представляет собою уравнение (n1)-й степени, а как известно уравнение (n1)-й степени не может иметь больше (n1) различных корней.

Дадим необходимое условие линейной зависимости n функций.

Предположим, что функции y₁,y₂,…y_n имеют производные порядка n1, и рассмотрим определитель:

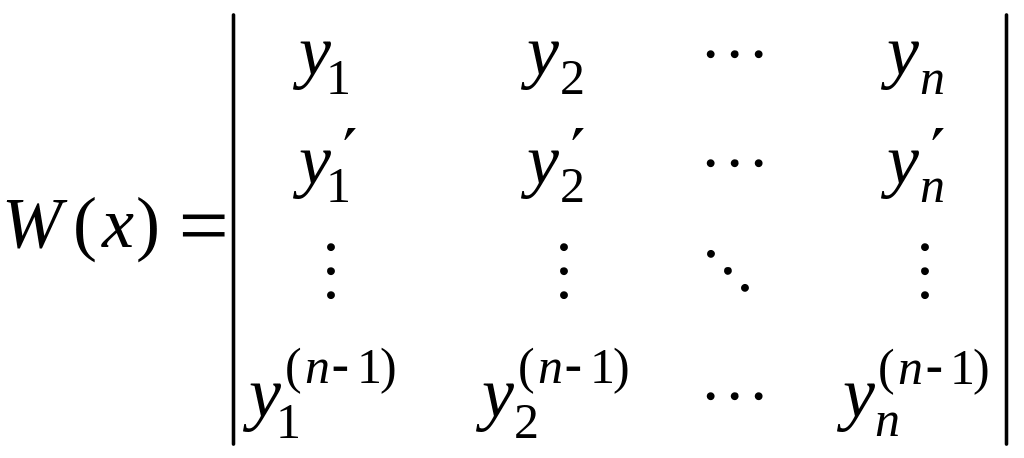. (4.6.22)

Этот определитель называется определителем Вронского для функций y₁,y₂,…y_n или вронскианом этих функций.

Теорема. Если функции y₁,y₂,…y_n линейно зависимы в интервале (a, b), то их вронскиан W(x) тождественно равен нулю в этом интервале.

Заметим, что это необходимое условие линейной зависимости n функций y₁,y₂,…y_n, но не достаточное.

Дадим необходимое и достаточное условие линейной независимости n решений однородного линейного уравнения n-го порядка. Пусть теперь каждая из функций y₁,y₂,…y_n есть решения уравнения (4.6.2). Тогда относительно вронскиана этих функций имеет место следующая теорема.

Теорема. Если функции y₁,y₂,…y_n линейно независимые решения уравнения (4.6.2), все коэффициенты которого непрерывны в интервале (a, b), то вронскиан этих решений W(x) не равен нулю ни в одной точке интервала (a,b).

Из этого следует, что для того, чтобы n решений уравнения (4.6.2) были линейно независимы в интервале (a, b), необходимо и достаточно, чтобы их вронскиан не обращался в нуль ни в одной точке этого интервала.

Однако оказывается, что для установления линейной независимости n решений уравнения (4.6.2) достаточно убедиться, что W(x) не обращается в нуль хоть в одной точке интервала (a, b).

Определение 7. Совокупность n решений однородного уравнения (4.6.2), определенных и линейно независимых в интервале (a, b), называется фундаментальной системой решений в этом интервале.

Из предыдущего следует, что для того, чтобы система n решений была фундаментальной, необходимо и достаточно, чтобы вронскиан этих решений был отличен от нуля хоть в одной точке интервала непрерывности коэффициентов уравнения (4.6.2). Все решения, входящие в фундаментальную систему, очевидно, ненулевые.

Значение n линейно независимых решений, т. е. фундаментальной системы решений, дает возможность построить решение уравнения (4.6.2), содержащее n произвольных постоянных, причем это решение будет общим решением. А именно, имеет место следующая теорема.

Основная теорема. Если y₁, y₂,...,y_n – фундаментальная система решений уравнения (4.6.2), то формула

y=C₁y₁+C₂y₂+…+C_ny_n, (4.6.23)

где C₁, C₂,..., C_n – произвольные постоянные числа, дает общее решение уравнения (4.6.2) в области

(4.6.24)

т. е. во всей области задания уравнения (4.6.2).

Уравнение (4.6.2) не может иметь более чем n линейно независимых частных решений. Действительно, пусть мы имеем n+1 частных решений. Рассмотрим первые n решений. Если они линейно зависимы, то и все наши n+1 решений линейно зависимы, ибо мы имеем соотношение

₁y₁+₂y₂+…+_ny_n+0y_n+1=0 (a<x<b), (4.6.25)

где не все  равны нулю. Если же решения линейно независимы, то, согласно основной теореме, всякое решение, в том числе и y_n+1, выражается линейно через:

(4.6.26)

так что решения y₁ y₂,...,y_n, y_n+1 снова оказываются линейно зависимыми.