Лекция 6.5. Формулы стокса и грина

6.5.1. Формулы Грина и Стокса

Формулы Грина и Стокса осуществляют преобразование циркуляции вектора по замкнутому контуру в двойной интеграл по поверхности, ограниченной этим контуром, причем формула Грина относится к плоскому полю, а формула Стокса – к пространственному. Хотя первая формула непосредственно следует из второй, приведем сначала независимый вывод формулы Грина из-за его простоты.

Рассмотрим циркуляцию плоского поля по замкнутому контуру L, проходимому в положительном направлении и ограничивающему плоскую конечную область S. Рассматриваемую циркуляцию в силу формулы (6.4.5) можно записать в виде

Ц .

Первый интеграл равен (рис. 6.5.1)

Рис. 6.5.1. Вычисление циркуляции плоского поля

Под знаком интеграла стоит частное приращение функции P по y, которое можно представить в виде интеграла от производной

.

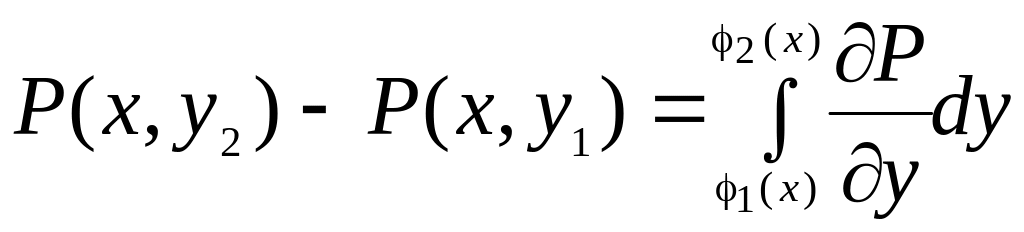Подставляя в , получаем

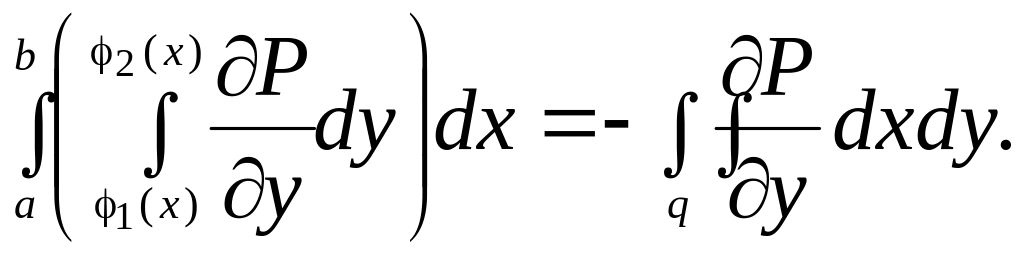
Аналогичное преобразование второго интеграла и сложение результатов приводят к формуле Грина

Этой формулой можно пользоваться, если все функции P, Q, конечны всюду в S.

Перейдем теперь к аналогичной формуле в пространстве. Эта формула, найденная в 1854 г. английским физиком и математиком Дж. Стоксом, широко применяется в теории векторного поля и является теоремой, которая характеризует свойства векторного поля в целом.

Физический смысл теоремы Стокса заключается в том, что циркуляция данного поля по любому замкнутому контуру равна потоку ротора через произвольную поверхность q, натянутую на этот контур. При этом нормаль к поверхности q согласуется с обходом контура по правилу правого винта.

Математически это записывают так (формула Стокса в векторной форме):

(rotF,n) .

В векторной форме теорему Стокса можно сформулировать так:

Теорема Стокса. Циркуляция вектора вдоль контура некоторой поверхности равна потоку вихря (ротора) через эту поверхность.

Доказательство. В качестве доказательства выведем формулу Стокса в векторной форме. Пусть некоторая поверхность q натянута на контур L. Разобьем эту поверхность на k малых частей , i = 1,2,…,k так, чтобы каждую часть можно было считать плоской. Элементарные части будут ограничены контурами L_i, а их площадь равна . Найдем поток ротора через i-ую часть. Для этого выберем в ней произвольную точку P_i (рис. 6.5.2).

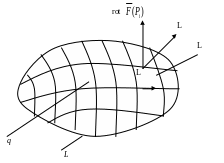
Рис. 6.5.2. Произвольная поверхность q, натянутая на контур L, в произвольном векторном поле

Согласно определению, плотность циркуляции поля в выбранной точке вокруг нормали к плоскости контура равна пределу

Ц

а её величина равна проекции ротора векторного поля в точке на нормаль к контуру , т.е.

(rot )

Если достаточно мала, то ротор внутри можно считать постоянным, а предел в правой части последнего равенства можно отбросить. Тогда поток ротора через элементарную часть поверхности приближенно будет равен

П (rot ) .

Поток через всю поверхность q равен сумме элементарных потоков

П (rot ) .

Переходя к пределу при , получим:

(rot ) .

Формула Стокса позволяет преобразовывать криволинейный интеграл по замкнутой пространственной линии в интеграл по поверхности.

В частном случае, когда векторное поле плоское, т.е.

= P(x,y) + Q(x,y) ,

ротор (вихрь) поля во всех его точках направлен параллельно оси (рис. 6.5.3).

Рис. 6.5.3. Схематическое изображение плоского векторного поля

Покажем это. Найдем координаты ротора плоского поля

rot ;

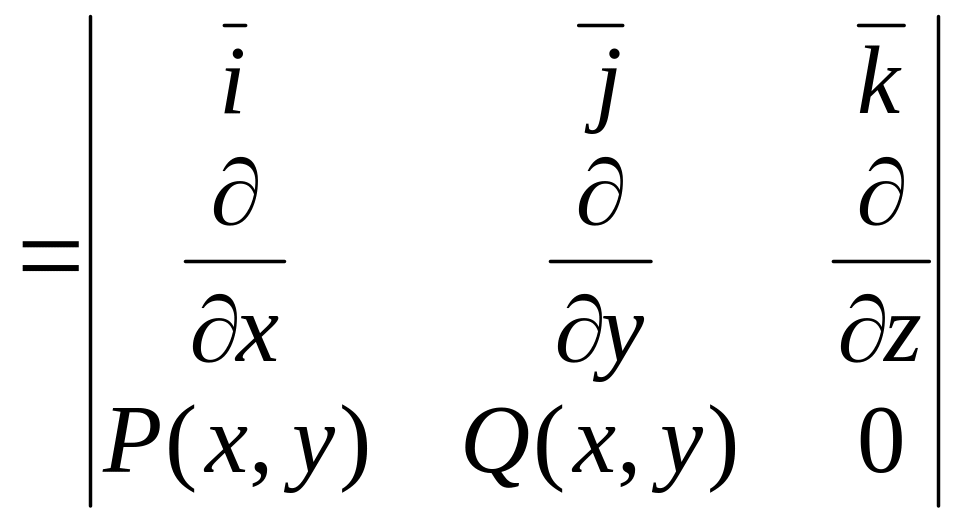rot = ;

rot = .

Проекции ротора на оси ox и oy равны нулю. В результате формула Стокса примет вид:

.

Таким образом, получили формулу Грина, «стартуя» с формулы Стокса.

Также при условии равенства нулю всех компонент ротора вектора, получаем, что криволинейный интеграл по любой пространственной кривой равен нулю, т.е. криволинейный интеграл не зависит от пути интегрирования.

Если раскрыть скалярное произведение векторов F и dl, стоящее под знаком криволинейного интеграла, а также выразить через координаты скалярное произведение векторов rot и n в правой части последнего равенства, то формула Стокса примет вид

Это равенство называют формулой Стокса в координатной форме.

Пример 1. Найти циркуляцию плоского векторного поля F(P,Q) по замкнутой кривой L в положительном направлении. F(2y,x), L – контур треугольника АВС, где А(0,0), В(1,0), С(1,1).

Решение. Вычислим циркуляцию, применив формулу Грина

Ц ,

где областью S является треугольник АВС. В нашем случае P=2y, Q=x. Следовательно, , . Тогда циркуляция поля F вдоль L равна

Ц .

Формула Стокса связывает криволинейные интегралы второго рода с поверхностными интегралами второго рода.

Пример 1. Вычислить циркуляцию векторного поля

вдоль линии L, состоящей из двух дуг полуокружностей радиуса a. Обход контура провести против часовой стрелки.

Решение. Проекции пространственного векторного поля на координатные оси:

; ; .

Циркуляция поля по данному контуру равна криволинейному интегралу

Ц .

Так как замкнутый контур L состоит из двух полуокружностей, то криволинейный интеграл по этому контуру можно заменить суммой двух криволинейных интегралов. Первый интеграл взять по дуге, расположенной в координатной плоскости xoz, второй – по дуге, лежащей в плоскости xoy:

,

.

На линии L₁: , лежащей в плоскости xoz, у=0; dy=0. С учетом этого, интеграл примет вид

Уравнение окружности для простоты вычислений лучше взять в параметрической форме: х=acost; z=asint, тогда dx=–asintdt; dz=acost dt. В результате первый интеграл сводится к линейному

.

Преобразуя подынтегральное выражение и расставляя пределы изменения параметра t с учетом обхода контура, получим

.

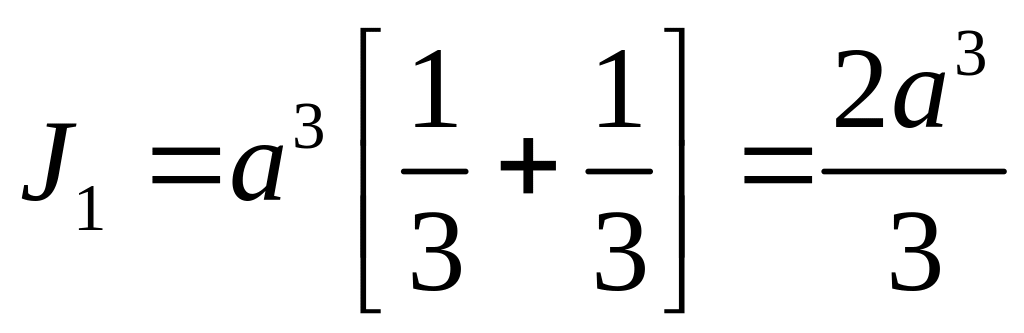На линии L₂: , лежащей в плоскости xoy, z = 0, dz = 0, тогда

.

Так же как и в первом интеграле, уравнение окружности возьмем в параметрической форме: х=acost; у=asint; dx=–asintdt; dу=acostdt.

Перейдем к линейному интегралу

,

,

.

Циркуляция поля по контуру L равна

Ц .

Теперь найдём циркуляцию данного поля по контуру L по теореме Стокса

(rotF

Для этого нужно определить координаты ротора, т.е.

Ц

Вычисляя частные производные, получим

Ц ,

т.е. ротор данного поля во всех точках параллелен оси , поле является плоско-параллельным.

Поверхность q₁ натянутая на контур L, однозначно проектируется на плоскость xoy, её проекцией является половина круга . Циркуляция поля равна двойному интегралу

Ц .

Так как областью интегрирования является полукруг, перейдем к полярным координатам

Ц .

Ц ,

Ц .

Циркуляция поля по данному контуру, найденная непосредственно и с помощью теоремы Стокса, имеет одно и тоже значение, при этом она отрицательна. Значит, вектор поля циркулирует в направлении, противоположном положительному обходу контура.

Вывод: мы вывели формулы связи между циркуляцией и ротором, сформулировали теоремы Грина и Стокса и дали их физическую интерпретацию.