7.2.6. Применение принципа сжатых отображений
Рассмотрим приложение принципа сжатых отображений к решению уравнений.
Заметим, что этот принцип находит большое применение при построении итерационных процессов для решения функциональных и дифференциальных уравнений.
Пусть в пространстве
,
составленном из непрерывных функций
,
задано отображение
,
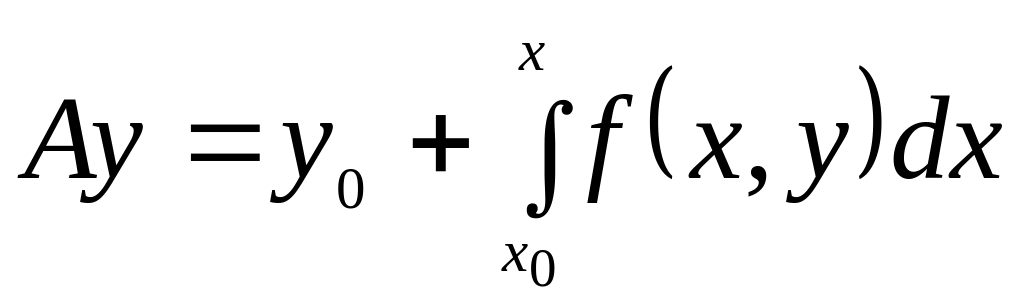где
- непрерывная функция, удовлетворяющая
в области G
условию Липшица (
,
где a,
b,
M,
N
- заданные числа), т.е. для любых двух
точек
области G
выполняется условие
,
где L
- некоторое неотрицательное число,
определяемое областью G
и не зависящее от положения точек
.
Покажем, что рассмотренное отображение
является сжатым при условии достаточной
малости
.
Действительно, пусть y и - произвольные точки пространства , тогда
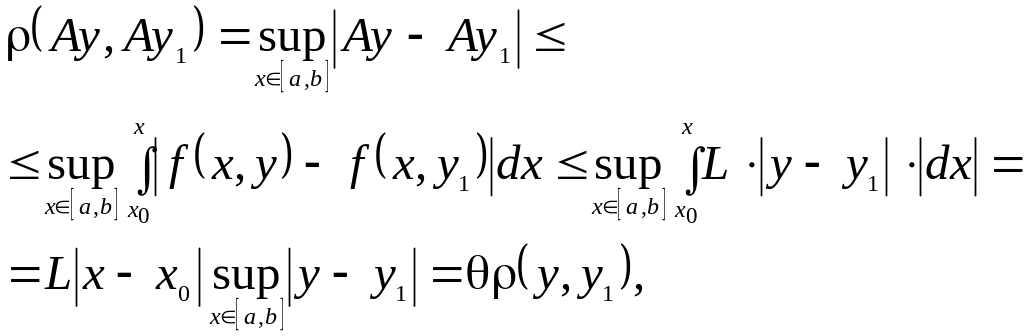
где
при
.
Из полноты
пространства
вытекает существование единственной
неподвижной точки сжатого отображения
A,
т.е. единственного непрерывного решения
уравнения
или интегрального уравнения
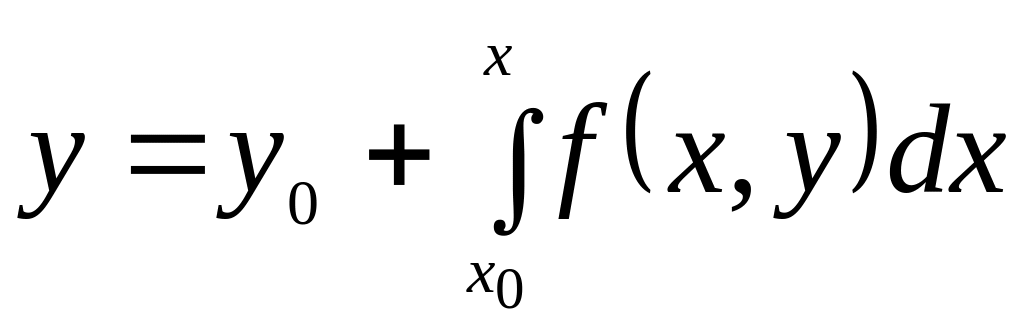(7.2.5)
при выполнении условий:
а) удовлетворяет условию Липшица с константой L;
б) (7.2.6)
Так как интегральное уравнение (7.2.5) эквивалентно дифференциальному уравнению
(7.2.7)
с начальными
условиями
,
то тем самым доказана теорема существования
и единственности решения для
дифференциального уравнения (7.2.7) при
выполнении условий (7.2.6).
Рассматривая
решение дифференциального уравнения
(7.2.7) как предел последовательности
функций
мы можем считать функции
последовательными приближениями
решения.
Пример 5.
Найти решение уравнения
,
если
- дифференцируемая функция при
и отображает отрезок
в
.
Если
,
то f
- оператор сжатия. Это следует из
неравенства
Существует единственное решение уравнения: , которое можно найти методом итерации.
Для произвольного
элемента
находим
и из точки
,
проводим прямую
до пересечения с прямой
.
Получаем точку
.
Далее, берем
и т.д. В пределе получаем точку
такую, что
.
Пример 6.
Пусть функция
непрерывна при
и такова, что удовлетворяет условию
Липшица по аргументу x,
т.е. для любых непрерывных на
функций
и
выполняется неравенство
,
где константа M не зависит от s и t. Показать, что решения интегрального уравнения
на подмножестве непрерывных функций на , удовлетворяющих условию
при
,
применим принцип сжатых отображений.
Пусть
- замкнутый шар в
,
т.е. множество функций из
таких, что
,
и пусть
,
тогда справедливо неравенство
.
В силу вышеуказанных
ограничений на величину
,
отсюда получим оценку
,
из которой заключаем, что оператор u
отображает множество
в себя. Далее, опираясь на условие
,
можно вывести соотношение
которое можно записать в виде
,
где в силу ограниченности для величины q справедлива оценка
.
Это означает, что для решения рассматриваемого интегрального уравнения применим принцип сжатых отображений.
Рассмотрим применение принципа сжатых отображений в алгебре.
Пусть дано алгебраическое или трансцендентное уравнение
. (7.2.8)
Предположим, что
функция
непрерывна, дифференцируема в промежутке
и удовлетворяет в этом промежутке
условиям
при
,
.
В этих условиях уравнение (7.2.8) имеет в промежутке единственный действительный корень.
Доказывается это также методом сжатых отображений. Рассмотрим множество действительных чисел как полное метрическое пространство с метрикой
,
отображаемое в
себя, и положим, что отображение
.
Если мы докажем
сжатость этого отображения, то тем самым
будет доказано существование единственной
неподвижной точки x,
или, другими словами, существование
единственного действительного корня
уравнения
,
.
Исходя из вышеизложенного, целесообразно рассмотреть применение принципа сжатых отображений в линейной алгебре на примере решения систем линейных алгебраических уравнений.
Пример 6.
Найти условия, при которых применим
принцип сжатых отображений для решения
системы линейных алгебраических
уравнений
,
где
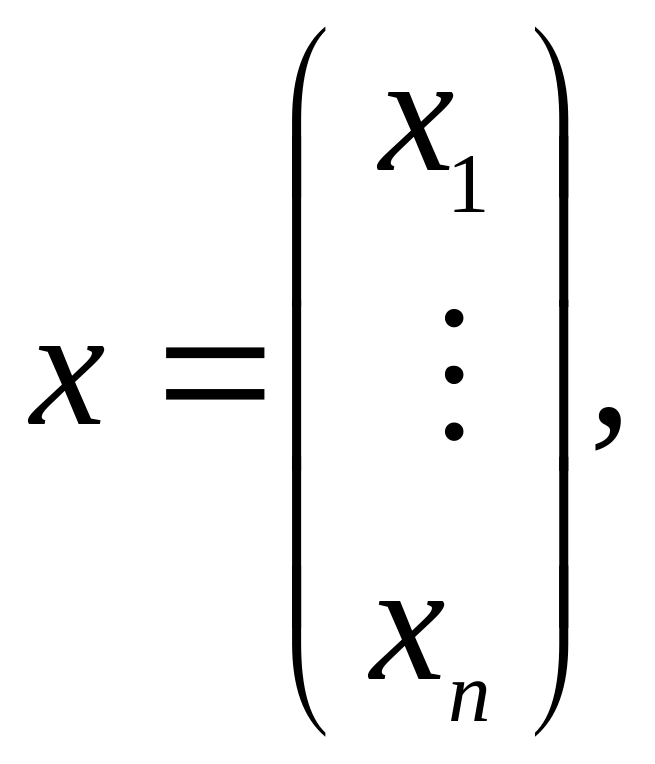
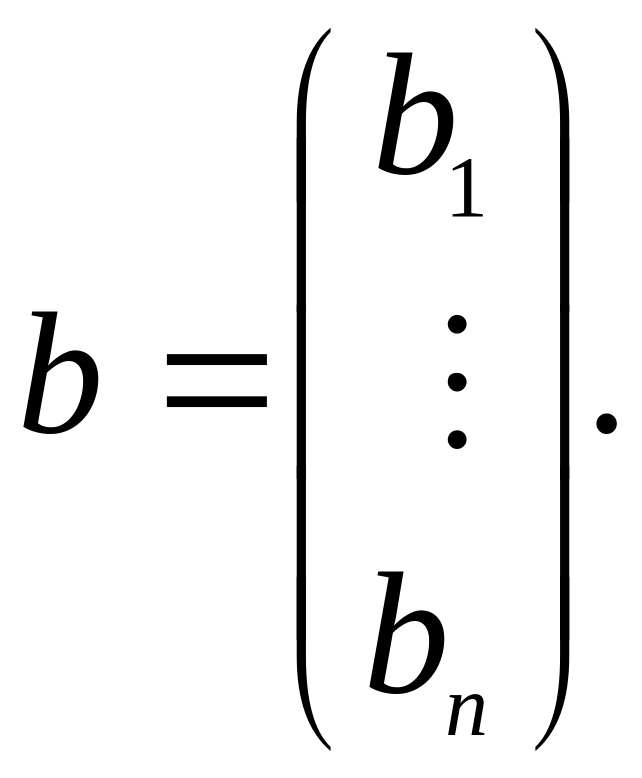
Рассмотрим оператор
,
где E
- единичная матрица. Тогда решением
системы уравнений будет неподвижная
точка оператора u,
отображающего n-мерные
векторы в n-мерные
векторы. Рассмотрим сначала n-мерные
векторы в пространстве
с метрикой
.
Найдем условия, при которых u является оператором сжатия. Применяя к внутренней сумме неравенство Коши, получаем оценку:
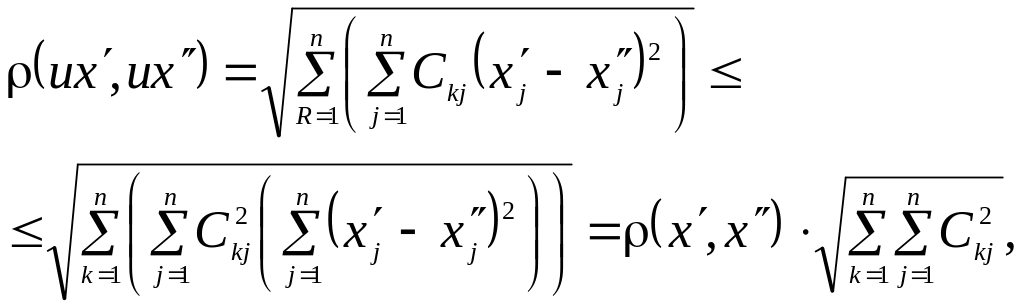
из которой следует, что если
,
где
то система уравнений имеет единственное решение, которое можно определить методом последовательных приближений.
Заметим, что если
число уравнений m
системы меньше числа неизвестных n
,
то
при
,
а потому
и принцип сжатых отображений не применим.
Если рассматривать
множество n-мерных
векторов в пространстве
с метрикой
,
то для образов
элементов
и
получим соотношение
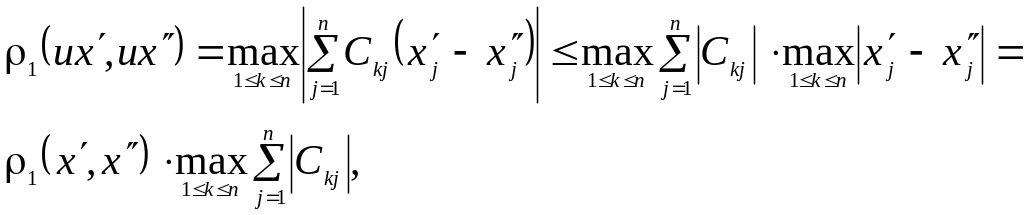
из которого следует, что если
,
то для решения системы применим принцип сжатых отображений.
Принцип сжатых
отображений можно применить и том
случае, когда замкнутый шар
полного метрического пространства X
отображается оператором A
в себя, т.е., когда
.
Из многочисленных
приложений метода сжатых отображений
в математическом анализе укажем только
одно. Пусть функция
определена в области
,
непрерывна по x
и имеет ограниченную производную по y,
такую, что
.
Тогда уравнение
имеет единственное непрерывное решение
на отрезке
.
Рассмотрим полное метрическое пространство всех непрерывных функций , определенных на отрезке , и отображение этого пространства в себя:
.
Докажем сжатость
этого отображения. Пусть
- точки пространства C.
Тогда
где
.
Следовательно, для любой точки
последовательность
,
сходится и
есть единственное непрерывное решение
уравнения (7.6.5), определенное на отрезке
,
и его последовательными приближениями
являются функции
.
Полученная при этом оценка имеет вид
.
Доказанная теорема существования неявной функции находит себе следующее практическое применение: пусть требуется вычислить значение непрерывной функции для данного значения аргумента в том случае, когда непосредственное вычисление этого значения затруднительно.
Тогда записывают
данную функцию в неявном виде
,
и если
непрерывная и имеет ограниченную
производную по y:
,
то
,
где
,
откуда получают:
.
Значение
неизвестно, его заменяют приближенным
значением
и далее пользуются итерационной формулой
Так, например, для
вычисления квадратного корня из числа
рассматривают функцию
,
формула для которой приобретает вид
(процесс Герона).
Если в этой формуле
положить
,
то уже на втором шаге получают результат
с точностью до
.
Метод итерации широко применяется в
вычислительной технике.
Заметим, что для итерационных процессов справедливо утверждение: последовательность элементов является фундаментальной.
Для доказательства существования решения какого-либо уравнения с помощью принципа сжатых отображений достаточно:
1) рассмотреть соответствующий этому отображению оператор;
2) показать, что этот оператор отображает полное метрическое пространство в себя;
3) убедиться, что этот оператор является сжатым.