Power Aspects of the Equivalent Circuit of an Antenna

Abstract

The Norton equivalent circuit of a receiving antenna consists of a current generator feeding two admittances in parallel, Y_a and Y_L. Admittance Y_L represents the load, and the power dissipated in Y_L, evaluated by “circuit” methods, correctly represents the actual electromagnetic power delivered to the load. The symbol Y_a represents the input admittance of the antenna radiating in its transmitting mode. Whether the power dissipated in Y_a, again evaluated by circuit methods, is equal to the power scattered by the antenna has been a matter of controversy for quite a few years. The present note seeks to review thet recurring problem.

1.Introduction

We shall derive the equivalent circuit of the typical antenna system shown in Figure 1, but the analysis can be extended to other types of antennas (see Section 6). The configuration consists of a load (a receiver), a pickup antenna (for example, a coaxial line). The main ideas of the analysis can be developed by making a few simplifying assumptions:

-The antenna radiates in free space

-The boundary walls of the antenna system are perfectly conducting, and

-The wave guide carries a single mode

The extension to multimode lines and to exterior regions V_e containing linear media (possibly anisotropic and/or nonreciprocal) is fairly straightforward, and is not germane to the present discussion.

If the waveguide carries only one mode, the transverse fields in the reference cross section S_g – chosen sufficiently far away from discontinuities for all non-propagating modes to be attemuated will be of the form

Where α is normalized according to the condition

In Figure 1, space is divided into two regions&

-The volume V_L of the load, bounded by S_g and the perfectly conducting walls, S_w and

-The exterior volume, V_e, bounded by S_g, S_w, and a spherical surface, S_∞, of very large radius.

The firlds in V_e, result from two contributions^

-The fields E_S, H_S, generated by the sources О in the presence of a metalized (short-circuited) surface, S_g, and

Хрень

• The fields E_a, H_a, due to the existence of a tangential electric field V α in the radiating aperture S_g (the transmitting mode)

When the antenna is fed from the left the ratio (-l)/V has a given value Y_a, namely, the admittance of the transmitting antenna. The radiated field is of the form E=Ce_a, In the far field, in particular

, (F_a dimensionless)

Similarly, on the load side, the ratio (I/V) has a given value Y_L

It is to be noted that the field problem embodied in Figure 1 is a particular case of the more general problem shown in Figure 2. Here, (u_nxE) is given on S_e, and J in V_e. The formal solution for E is

In this equation, V_e is the volume exterior to S_e, r₀ is an exterior point, and the (Green’s) dyadic is formed from the column vectors G_x, G_y, G_z. Thus

Vector for example, is the solution of

-curlcurl

Формула

Where satisfies the radiated conditions. In Equation

Is a Huygens equivalent magnetic current

In the application of Equation to Figure 1 J_mS is on S_g, and it

vanishes on S_w Thus,

The first term on the right-hand side is the field, E_s, generated by О in the presence of a short-circuited S_g. The second term is the contribution from the antenna. It has been previously denoted by Ve_a, hence we write

In the far field

The fields E_S, H_S, can further be split into the incident fields, E_i, H_i generated by the currents О radiating in free space, and the scantered fields, E_SC, H_SC, generated by the currebts induced on S_w and the metalized S_g. In V_e we write

Or

2. The Equivalent Circuit of the Receiving Antenna

On the basis of Maxwell’s equations, satisfied by both the “s” and “a” fields

Integrating over all space (but excluding the volume V_L of the load) yields

This equation is obtained by involving the following properties:

1. E_a and E_s are perpendicular to the perfectly conducting walls properties, S_w

2. E_s is perpendicular to S_g

3. The “a” and “s” fields satisfy the radiation conditions, hence the bracketed term in Equation is O(l/R³) at large distances R. The contribution from a large spherical surface of radius К there-fore vanishes in the

limit

In the “s” pattern, the transverse magnetic field on S_g is

Where l_g is the short-circuit current induced under illumination by the exterior sources J. Alternately, the the short-circuit current density on S_g is

In Equation, we may set E_a-V_aα. On the basis of Equation, this gives

In the configuration of Figure 1, an equivalent voltage V_a, appears in cross section S_g, to the left of S_g

To the right of S_g,

Expressing continuity of H_t across S_g gives

The Norton equivalent circuit of Figure 3 expresses these relationships. It can be invoked to predict the fields. It can also be used to evaluate the power flowing to the load. This is done by applying Poynting's the orem (discussed in Section 31) to Y_L. Thus, using peak values for field quantities,

where g_L=ReY_L. This is the power budget dor the enclosed volume V_L of the load, assumed to contain only passive materials. Wу note that Poynting's vector is tangent to the metallic walls, and hence that is flux throught the boundary of V_L reduces to the flux throught S_g.

The electromagnetically derived power, Equation, is also the value predicted by circuit theory. For the power dissipated in Y_a, circuit theory would also give

Central to the discussion in whether P_a has any electromagnetic meaning, for example, in terms of the power scattered by the antenna. Under matched conditions, with Y_a = Y_L, P_a=P_L, one could (erroneously) conclude that only half the available power goes to the matched load, while the other half is reradiated back to the space from whence it came. Under these circumstances, the antenna absorption efficiency could not exceed 50℅, an apparent paradox. There are consequently reasons to wonder whether the equivalent circuit, which correctly to evaluate radiated power from the receiving antenna. Such doubts were already voiced more than half a century ago by Silver, who wrote that the radiated energy was modified by the interaction between the fields. This remark forms the basis of the arguments presented in the next section.

3. Power Budget for Two Sources

Consider first a single source of current, J, immersed in a volume, V, bounded by a surface, S. By inserting Maxwell’s equations into the relationship

One obtains

Хрень

Integrating this expression over V leads to the (real) power budget

The surface term is the power radiated to the region exterior to S, and the volume term represents the power, P^J,, furnished by the sources

The same kind of analysis can now be applied to a system of two sources, J₁ and J₂, (which may be considered to form a simple two-element array). When they radiate individually in space, these sources generate respective fields

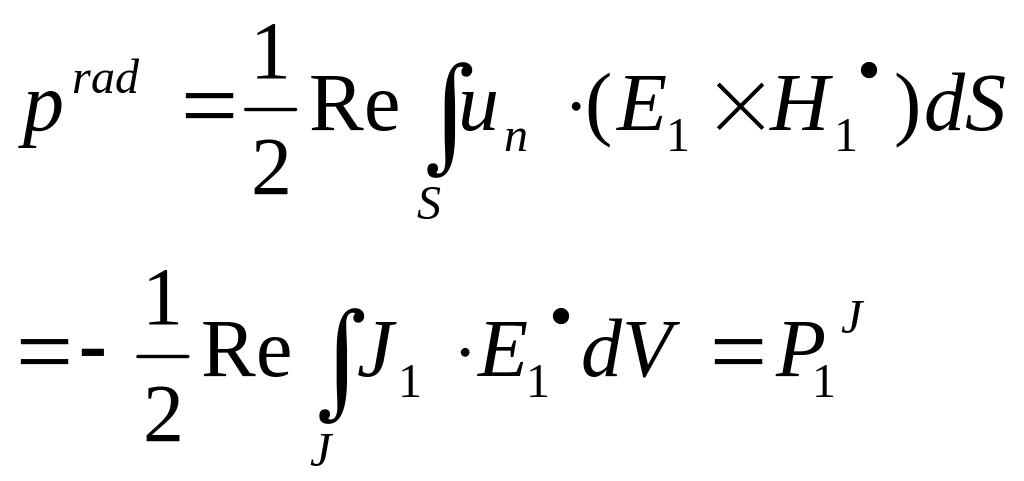
A similar relationships holds for the “2” fields. When equation is applied to the total field E=E₁+E₂, H=H₁+H₂ it yields

The surface integral may be written in more detail as

Формула

The first two terms are the powers radiated individually by J₁, and J₂, and the third term is a power interaction term, which must be carefully kept in the analysis. It is clear from the presence of that “combined” term that radiated powers do not add up, except under special conditions. The point is illustrated by the examples discussed in Section 4. On the source side of Equation, we may similarly write.

Формула

Here again the combined effects за the sources generate an interaction term, which may either increase or decrease the total power provided by the sources with respect to the sun of the individual powers.

In the evalution of scattered fields, surface S is often taken to be a spherical surface of very large radius R, on which the fields have their far-field values

Формула

In these expressions, К is the distance to a common phase-refence point, O, F₁ and F₂ are functions of 0 and φ, and R_o is the characteristic impedance, of free space. The radiated power, Equation, now becomes

Формула

Where is on elementary solid angle, and the integration is over all directions.

In many applications, J₁ is the source of an incident field and J₂ represents the correction induced in a scatterer. For such a case, (E₂H₂) are the scattered fields (E_SC,H_SC). If the incident fields are those of a plane wave

Формула

We note it

Формула

Is the power scattered by the obstacle, assumed to radiate alone in space, while

Формула

May be called the excitation power.

4. A Few Simple Combined Sources

This section illustrates the influence of the interaction term by discussing four very simple problems. The first one concerns the two-dimensional configuration of two z-oriented currents, I₁ and I₂. The radiated fields from a single current, I, are of the form

Формула

The power radiated by that source (in W per m along the axis) is

Формула

In the presence of two equal sources (i.e., with I₁=I₂=I) the total far fields is

Формула

Giving a radiated power

Формула

The factor is the sun of the individually radiated powers. The integral in the term between brackets therefore represents the influence of the interaction term. At small distances, i.e., for k_ol<1, this term approaches one, hence P^rad becomes four times the power radiated by I, or, equivalently, the power radiated by 2l.

For anti-parallel currents (i.e., for I₁=-I₂=I)

Формула

At small (k_ol), the two currents form a dipole line, and the two sources together radiate a power

Формула

That power approaches zero with k_ol, fundamentally because (+I) and (-I) interfere more and more destructively as their mutual distance decreases.

The same kind of behavior holds in three dimensions. For example, consider the two equal electric dipoles shown in Figure 66. The fields stemming from P_el are

Формула

With respect to the phase center, O.

Хрень

The power radiated by an individual dipole is easily found to be

Формула

For the two dipoles together,

Формула

The leading factor is the sum of the individual radiated powers. The double integral term represents the interaction. For small (k_ol), P^rad becomes

Формула

Assume, as a final exercise, that P_el in Figure 6b is left untouched, but that P_e2 is replaced by a similarly located and oriented magnetic dipole P_m. The radiation fields of P_m are

Формула

A few simple steps show that

Формула

From which it follows that the total radiated power is the sum of the individual powers. There is no interaction in that case: “power orthogonality” holds.

5. Back to the Equivalent Circuit

In this epoch-making memoir, Pointing essentially derived the power budget described in Equation. He also mentioned that the energy flows perpendicularly to the plane containing the lines of force e and h. The possibility of attaching such a local meaning to power –density relationship, Equation, has been a matter of controversy for quite a few years. From a local point of view, div (e x b) is the deposit of energy per unit volume per second, and e x h is the flux of electromagnetic power at any place. Under these assumptions, the flux of power through an open surface, such as cross section S_g in the receiving mode of the antenna cannot be related to the “scattered power”, since the flux to the rights is equal to minus P^L. It follows that the power budget in an enclosed volume is the only aspect of interest of our analysis. The relevant volume is V_e, and the boundary surface consists of S, cross section S_g, and the exterior walls S_w of the load (Figure 1). According to Equation (7), there are two² simultaneously radiating sources, J and Формула

The power budget of Equation (26) now takes the form

Формула

On the basis of Equation (28), the radiated power consists of three terms:

Формула

Or

Формула

The first term is due to the source radiating in the presence of a short-circuited S_g. The second and third terms represent the contribution of the magnetic current (u_n x E). We note that from Equation(19), P^rad₂ is precisely the power, Equation (23), evaluated by the rules of circuit theory. The proof rests on the fact that in the transmitting mode, the flux of power through S_g is equal to the flux through S. The forst flux is