Методичка по лабораторной работе №4 [новая]

Обобщим алгоритм на тот случай, когда некоторые дуги имеют отрицательные длины. При выполнении шага 2 алгоритма пересчет вели­чин d(x) производят для всех вершин.

Если для некоторой окрашенной вершины вели­чина d(x) уменьшается, то с нее и с инцидентной ей дуги окраску снимают.

Процесс вычислений заканчивают, когда все вер­шины графа G окрашены и ни одно из чисел d(x) не меняется при пересчете.

Пример. На рис. 1.21 изображен граф, имеющий дугу отрицательной длины. Найти кратчайший путь между вершинами s я t.

Окрашиваем вершину s. Полагаем , пересчитываем величины d(x): .

Окрашиваем вершину t, дугу(s, t) и полагаем y=t. Пересчитываем числа d(x). Поскольку из вершины t не исходит на одна дуга, эти числа не меняются.

Окрашиваем вершину а и дугу (s, а). Полагаем у=a и пересчитываем d(x): . Величина d(t) уменьшилась, поэтому с вершины t и дуги (s, t) окраску снимаем.

В исходном графе неокрашенной является только вер­шина t. Она окрашивается вместе с дугой (a, t), по­скольку у=а.

Полагая y=t, пересчитываем величины d(x), но они не меняются. Кратчайшим является путь (s, a, t).

Описанный алгоритм можно применять к задаче поиска кратчайших путей между каждой парой вершин графа. Однако эта процедура требует больших вычислений и обычно для решения применяют специальный алгоритм.

Алгоритм Флойда

Дано: непустой взвешенный граф G=(V, E) с произвольными весами ребер (дуг) - . Требуется найти длины кратчайших путей между всеми парами вершин графа, если в графе нет циклов (контуров) отрицательной суммарной длины, либо обнаружить наличие таких контуров.

Инициализация:

1. Построим матрицу размерности , элементы которой определяются по правилу:

d_ij⁰= a(v_i, v_j), где i<>j, если в графе существует ребро (дуга) (v_i, v_j);

, где i<>j, если нет ребра (дуги) (v_i, v_j).

2. m = 0.

Основная часть:

1. Построим матрицу D^m+1 по D^m, вычисляя ее элементы следующим образом:

d_ij^m+1=min{d_ij^m, d_i(m+1)^m + d_(m+1)j^m}, где i<>j; d_ii^m+1=0 (*).

Если d_im^m + d_mi^m < 0 для какого-то i, то в графе существует цикл (контур) отрицательной длины, проходящий через вершину v_i. Выход.

2. m:=m+1; если m<|V|, то повторяем шаг (1), иначе элементы последней построенной матрицы D^|V| равны длинам кратчайших путей между соответствующими вершинами. Выход.

Конец .

Если требует найти сами пути, то перед началом работы алгоритма построим матрицу P с начальными значениями элементов p_ij=i. Каждый раз, когда на шаге (1) значение d_ij^m+1 будет уменьшаться в соответствии с (*) (т.е. когда d_i(m+1)^m + d_(m+1)j^m<d_ij^m), выполним присваивание p_ij:=p_(m+1)j. В конце работы алгоритма матрица P будет определять кратчайшие пути между всеми парами вершин: значение p_ij будет равно номеру предпоследней вершины в пути между i и j (либо p_ij=i, если путь не существует).

Примечаниe: если граф - неориентированный, то все матрицы D^m являются симметричными, поэтому достаточно вычислять элементы, находящиеся только выше (либо только ниже) главной диагонали.

Алгоритм построения деревьев

Пусть имеется некоторый граф G и каждому его ребру (х, у) поставлено в соответствие число m(x, y), которое называется его весом.

Вес дерева определяется как сумма весов составляю­щих его ребер. Для графа G необходимо построить покрывающее дерево минимального веса.

Алгоритм построения минимального по­крывающего дерева

Просматривают ребра графа G в порядке возрастания их весов. Если ребро включается в покрывающее дерево, то его окрашивают в голубой цвет, в противном случае – в оранжевый цвет. Ребра, включенные в дерево, образуют граф, состоящий из нескольких компонент. Если конце­вые вершины просматриваемого ребра принадлежат одной и той же компоненте, то ребро образует цикл с ребрами, ранее включенными в дерево. Такое ребро не включают в дерево. В противном случае ребро включают в дерево. Вершины одной связной компоненты составляют букет.

1. Берут любое ребро, не являющееся петлей. Окра­шивают его в голубой цвет, а его концевые вершины включают в первый букет.

2. Выбирают неокрашенное ребро.

Если его концевые вершины принадлежат одному и тому же букету, то окрашивают ребро в оранжевый цвет. Если ни одна из его концевых вершин не принадле­жит ни одному из букетов, то включают их в новый бу­кет и окрашивают ребро в голубой цвет. Если концевые вершины принадлежат разным буке­там, то объединяют эти букеты в один и окрашивают ребро в голубой цвет. Если один конец ребра принадлежит некоторому бу­кету, а второй не входит ни в один букет, то нужно включить второй конец в тот же букет и окрасить ребро в голубой цвет.

3. Заканчивают процедуру, если все вершины графа вошли в один букет. В противном случае переходят к шагу 2.

Число шагов при выполнении алгоритма конечно, так как оно не превышает числа ребер графа. Если голубые ребра не образуют покрывающего дерева, то у исходного графа его нет.

Пример. В новом районе имеется шесть жилых мас­сивов. Нужно соединить их между собой дорогами, стои­мость прокладки которых была бы минимальна. В сле­дующей таблице приведены стоимости постройки дорог между каждой парой жилых массивов:

	a	b	c	d	e	f
a	-	12	1	13	11	10
b	12	-	14	3	5	12
c	1	14	-	16	17	15
d	13	3	16	-	5	7
e	11	5	17	5	-	6
f	10	12	15	7	6	-

Решение задачи запишем в виде следующей таблицы:

Ребро	Цвет	Букет 1	Букет 2
(a, c)	Голубой	a, c
(b, d)	Голубой	a, c	b, d
(d, e)	Голубой	a, c	b, d, e
(b, e)	Оранжевый	a, c	b, d, e
(e, f)	Голубой	a, c	b, d, e, f
(d, f)	Оранжевый	a, c	b, d, e, f
(a, f)	Голубой	a, b, c, d, e, f

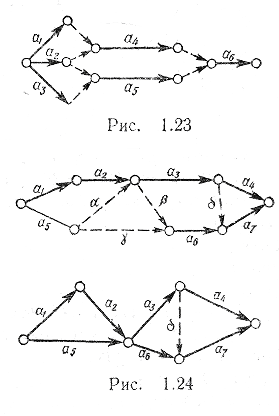
Построено покрывающее дерево, вес ко­торого равен 25 (рис, 1.22).

Задачи сетевого планирования

Сетевое планирование применяют для организации и составления календарных планов реализации больших комплексов работ. Это, например, научно-исследовательские работы с участием нескольких институтов, разработка автоматизированной системы бух­галтерского учета, строительство большого объекта и т. д. Управление всеми этими работами можно осуществлять с помощью метода критического пути. Использование этого метода позволяет сравнительно просто выяснить, когда необходимо начинать и заканчивать выполнение отдельных операций, как задержка хода выполнения некоторой опе­рации влияет на время завершения всего проекта.

Для использования метода критического пути нужно прежде всего разбить крупный проект на отдельные опе­рации и составить перечень операции. Некоторые из них могут выполняться одновременно, другие – только в опре­деленном порядке. Например, при строительстве дома нельзя возводить стены раньше, чем сделан фундамент. Необходимо выяснить очередность выполнения всех опе­раций списка. Для этого составляют список операций, непосредственно предшествующих каждой операции. После этого нужно запланировать время, необходимое для вы­полнения каждой операции. Полученные данные обычно помещаются в таблицу. В табл. 11.1 приведены данные для проекта, состоящего из шести работ. Для каждой из них задана продолжительность и указаны непосредственно предшествующие ей операции.

При построении графа каждую операцию изображают в виде ориентированной дуги. Связи между операциями также представляются в виде дуги. Дугу-связь проводят из конца дуги, соответствующей предшествующей опера­ции, в начало следующей операции. Чтобы отличить опера­ции от связей, операции изображают сплошными линиями, а связи – пунктирами. Вершины графа называют собы­тиями. Временем наступления события считают время, когда завершено выполнение всех операций, входящих в соответствующую вершину.

Операция	Предшествующие операции	Время
a1	-	10
a2	-	5
a3	-	15
a4	a1a2	18
a5	a2a3	19
a6	a4a5	18

Граф, представляющий взаимосвязь отдельных работ проекта, называется сетевым графиком. На рис. 1.23. построен сетевой график для комплекса операций, зада­ваемых таблицей.

Большое количество дуг в сети усложняет решение задачи. Поэтому прежде всего нужно упростить получен­ную сеть. Для этого можно выбросить некоторые дуги-связи. Начало и конец выбрасываемой дуги объединяют в одну вершину. При этом нужно проверять, не нару­шится ли порядок выполнения операций после выбрасы­вания дуги. Проверку проводят по таблице, задающей проект.

Задание на лабораторную работу

1. Ознакомиться с методами решения задач с сетевым представлением.

2. В соответствии с вариантом задания, определенным преподавателем, составить программы, реализующие метод решения.

3. Оформить отчет о выполнении задания с приведением условия задачи, алгоритмов и программ указанных методов, результаты решения.

Варианты заданий

1. В модульных перевозках груженые трейлерные платформы перевозятся по железной дороге между специальными перевалочными железнодорожными терминалами, где платформы снова присоединяются к трейлерам и далее следуют к потребителям автомобильным ходом. На рис. 1 показаны основные железнодорожные терминалы Соединенных Штатов и существующие железнодорожные пути между ними. Выделите сегменты железных дорог так, чтобы были связаны все железнодорожные терминалы и была минимизирована суммарная стоимость перевозок трейлерных платформ (стоимость перевозок пропорциональна длине железнодорожных путей).

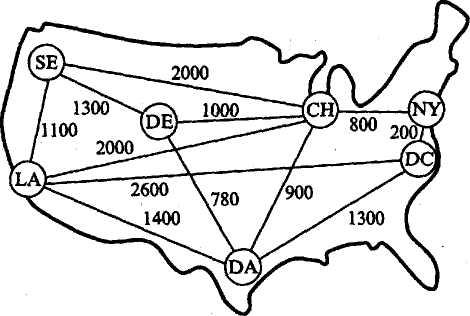
Рис. 1

2. Ha рис. 2 показаны расстояния между платформами, добывающими газ в открытом море, и приемным пунктом, расположенным на берегу. Поскольку платформа 1 ближе остальных к берегу, она оснащена необходимым оборудованием для перекачки газа от остальных платформ к приемному пункту. Спроектируйте сеть трубопроводов минимальной длины, соединяющую приемный пункт со всеми добывающими платформами.

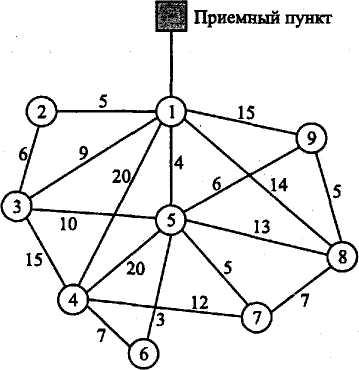
Рис. 2

3. Предположим, что в предыдущей задаче (рис. 2) все добывающие платформы разбиты на две группы в зависимости от давления газа в скважинах: к группе с высоким давлением газа относятся платформы 2, 3, 4 и 6, с низким давлением —5, 7, 8 и 9. Из–за разницы в давлении газопроводы от платформ разных групп нельзя соединять между собой. В то же время газопроводы от этих групп могут подсоединяться к приемному пункту через платформу 1. Определите минимальную сеть трубопроводов для данной ситуации.

4. Компания производит 15 типов изделий на 10 станках. Компания планирует сгруппировать станки так, чтобы минимизировать "несходство" операций, выполняемых на каждой группе станков. Мерой "несходства" между станками i и у служит величина d_y, вычисляемая по формуле

где n_ij —количество изделий, обрабатываемых как на станке i, так и на станке j, m_ij — количество изделий, обрабатываемых только на станке i или только на станке j.

В следующей таблице показано, изделия каких типов на каких станках обрабатываются.

Станок	Типы изделий
1	1,6
2	2, 3, 7, 8, 9, 12, 13, 15
3	3, 5, 10, 14
4	2,7,8,11,12,13
5	3,5,10,11,14
6	1,4,5,9,10
7	2,5,7,9,10
8	3,4,15
9	4,10
10	3, 8, 10, 14, 15

Сформулируйте данную задачу как сетевую.

Покажите, что разбиение множества станков на группы можно получить как решение задачи нахождения минимального остовного дерева.

Решите данную задачу для множества разбиения станков на две и три группы.

5. Компания по прокату автомобилей разрабатывает план по обновлению парка своих машин на следующие пять лет (2000–2004 гг.). Каждый автомобиль должен проработать не менее 2–х и не более 4–х лет. В следующей таблице приведена стоимость замены автомобиля в зависимости от года покупки и срока эксплуатации.

	Стоимость замены ($) в зависимости от срока эксплуатации
Год покупки	1	2	3
2000	3800	4100	6800
2001	4000	4800	7000
2002	4200	5100	7200
2003	4800	5700	—
2004	5300	—	—

6. На рис. 3 показана коммуникационная сеть между двумя приемно–передающими станциями 1 и 7. Возле каждой дуги этой сети указаны вероятности передачи сообщений без потерь по этим дугам. Необходимо найти маршрут от станции 1 к станции 7 с максимальной вероятностью успешной передачи сообщений. Сформулируйте эту задачу как нахождение кратчайшего пути и решите.

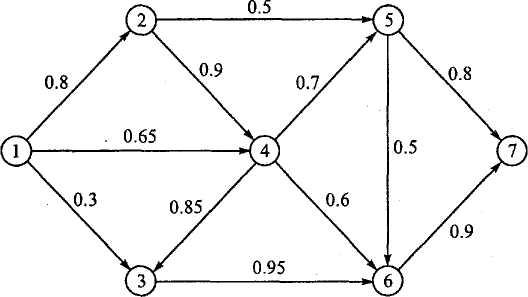
Рис. 3

7. Тостер старой конструкции имеет две подпружиненные дверцы на петлях, размещенные с обеих сторон тостера. Ломтик хлеба помещается в тостер с одной стороны и дверца закрывается, затем другой ломтик хлеба загружается в тостер с противоположной стороны. После того как одна сторона ломтика хлеба подрумянится, он переворачивается. Задача заключается в определении последовательности операций (помещение ломтика хлеба, поджаривание одной стороны, переворачивание ломтика в тостере и извлечение готового хлеба из тостера), необходимых для поджаривания трех ломтиков хлеба за минимально возможное время. Сформулируйте эту задачу как нахождение кратчайшего пути, используя следующие данные о времени выполнения различных операций.

Операция	Время (секунды)
Помещение ломтика хлеба в тостер	3
Поджаривание одной стороны ломтика	30
Переворачивание ломтика в тостере	1
Извлечение ломтика из тостера	3

8. Планирование производства. Компания продает некую продукцию, спрос на которую в следующие 4 месяца составит 100, 140, 210 и 180 единиц соответственно. Компания может удовлетворить любой помесячный спрос на продукцию и даже спрос на два и более месяца вперед. В последнем случае необходимо платить $ 1.20 за хранение единицы избыточно произведенной продукции в течение месяца. Покупная цена единицы продукции в следующие 4 месяца будет равна $15,$12, $10 и S14 соответственно. Стоимость переналадки оборудования для выполнения заказа составляет $200. Компания хочет разработать такой производственный план, чтобы минимизировать расходы на выполнение заказов, покупку продукции и ее хранение. Сформулируйте задачу как нахождение кратчайшего пути и найдите ее оптимальное решение.

9.Задача о рюкзаке. Путешественник, собираясь в путь, пытается поместить в свой рюкзак, объемом 5 кубических футов, наиболее необходимые в путешествии вещи. Имеется три вещи, объемом соответственно 2, 3 и 4 кубических фута, необходимость в которых оценивается (по 100–балльной шкале) в 30, 50 и 70 баллов. Сформулируйте эту задачу как сетевую, где необходимо определить самый длинный путь, и найдите ее оптимальное решение. (Совет. Узел в этой сети можно определить как пару [i, v], где i — номер выбираемой вещи, a v— свободный объем рюкзака, оставшийся после выбора i–й вещи.)

10. На рис. 4 показана транспортная сеть, соединяющая восемь городов, и расстояния между ними. Найдите кратчайшие маршруты между следующими городами.

1. Между городами 1 и 8.

2. Между городами 1 и 6.

3. Между городами 4 и 8.

4. Между городами 2 и 6.

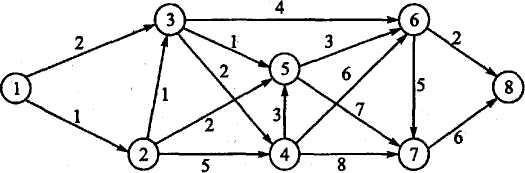
Рис. 4

11. Найдите кратчайшие пути между узлом 1 и всеми остальными узлами сети, представленной на рис. 5.

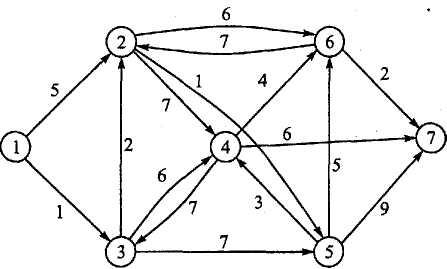
Рис. 5

12. Примените алгоритм Флойда к сети, показанной на рис. 6. Заметьте, что ребра (7, 6) и (6,4) ориентированы. Определите кратчайшие пути между следующими парами узлов.

1. От узла 1 к узлу 7.

2. От узла 7 к узлу 1.

3. От узла 6 к узлу 7.

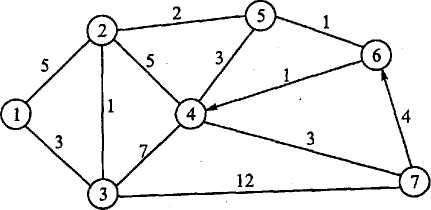
Рис. 6

13. Телефонная компания обслуживает шесть удаленных друг от друга районов, которые связаны сетью, показанной на рис. 7. Расстояния на схеме сети указаны в милях. Компании необходимо определить наиболее эффективные маршруты пересылки сообщений между любыми двумя районами.

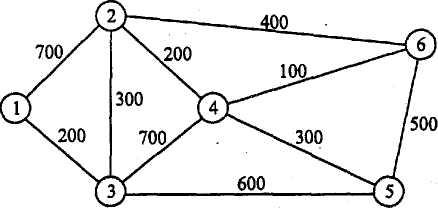
Рис. 7

14. Найдите максимальный поток и значения потоков, проходящих через каждое ребро сети, показанной на рис. 8.

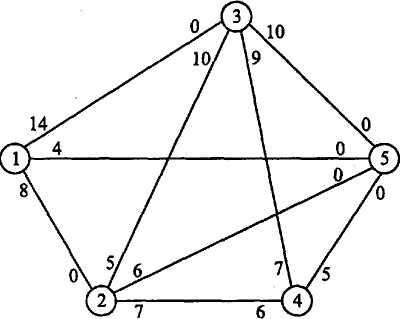
Рис. 8

15. Три нефтеперегонных завода транспортируют свою продукцию двум распределительным терминалам по сети трубопроводов, которая включает и насосные станции (рис. 9). Направления потоков в сети показаны стрелками, пропускные способности отдельных сегментов сети указаны в миллионах баррелей в день.

Рис. 9

Определите ежедневную производительность каждого нефтеперегонного завода, соответствующую максимальной пропускной способности сети трубопроводов.

Определите ежедневную потребность каждого распределительного терминала, соответствующую максимальной пропускной способности сети трубопроводов.

Определите ежедневную пропускную способность каждой насосной станции, соответствующую максимальной пропускной способности сети трубопроводов.

15. Пусть в сети из предыдущего упражнения (рис. 9) пропускная способность насосной станции 6 ограничена 60 миллионами баррелей в день. Найдите максимальную пропускную способность сети с учетом этого ограничения.

16. Зерно из трех зернохранилищ доставляется на грузовиках четырем птицеводческим фермам, при этом некоторые зернохранилища не могут непосредственно поставлять зерно определенным фермам. Пропускная способность маршрутов от зернохранилищ до птицеводческих ферм ограничена количеством используемых грузовиков и числом выполняемых ежедневно рейсов. В следующей таблице показаны ежедневные предложения зернохранилищ и ежедневный спрос птицеводческих ферм (в тысячах фунтов), в ячейках таблицы указаны пропускные способности соответствующих маршрутов.

		1	2	3	4
Зернохранилища	1	30	5	0	40	20
	2	0	0	5	90	20
	3	100	40	30	40	200
		200	10	60	20