Методичка по лабораторной работе №4 [новая]

Теория принятия решения

Лабораторная работа №4

Тема: Сетевые модели.

Цель работы

Знакомство с задачами , использующими сетевые модели представления, изучение различных методов решения в системе компьютерной математики.

Краткие теоретические сведения

Основные понятия теории графов

Граф G—это совокупность двух конечных множеств: множества точек, которые называются вершинами, и мно­жества пар вершин, которые называются ребрами.

На рис. 1.1 изображен граф, имеющий пять вершин и шесть ребер.

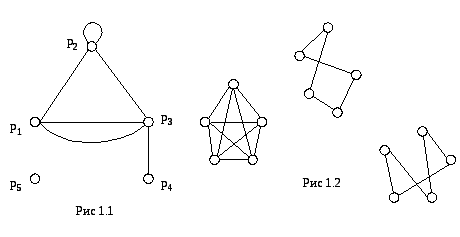
Если рассматривается множество упорядоченных пар точек, т. е. на каждом ребре задается направление, то граф G называется ориентированным. В противном случае G называется неориентированным графом.

Ребра, имеющие одинаковые концевые вершины, назы­ваются параллельными.

Ребро, концевые вершины которого совпадают, назы­вается петлей. На рис. 11.1и – параллельные ребра, а – петля.

Вершина и ребро называются инцидентными друг другу, если вершина является для этого ребра концевой точкой. На рис. 11.1 вершинаи ребро инцидентны друг другу.

Две вершины, являющиеся концевыми для некоторого ребра, называются смежными вершинами. Два ребра, инци­дентные одной и той же вершине, называются смежными ребрами. На рис. 1.1 – смежные вершины, – смежные ребра,

Степенью вершины называется число ребер, инцидент­ных ей. Вершина степени 1 называется висячей. Вершина степени 0 называется изолированной. На рис. 1.1 степень вершины равна трем, – висячая вершина, – изо­лированная.

Граф G называется полным, если любые две его раз­личные вершины соединены ребром и он не содержит параллельных ребер.

Дополнением графа G называется граф с теми же вершинами, что и граф G, и содержащий только те ребра, которые нужно добавить к графу G, чтобы получился полный граф. На рис. 1.2 изображены следующие графы: G₁ –полный граф с пятью вершинами, G₂ – некоторый граф, имеющий пять вершин, – дополнение графа G₂.

Путем в графе называется такая последовательность ребер, ведущая от некоторой начальной вершины p₁ в ко­нечную вершину p_n, в которой каждые два соседних ребра имеют общую вершину и никакое ребро не встречается более одного раза. Например, в графе, изображенном на рис, 1.1, последовательность реберобразует путь, ведущий от вершины p₁ к вершине р₄.

Циклом называется путь, начальная и конечная вер­шины которого совпадают. На рис. 11.1 ребра образуют цикл.

Цикл графа G называется простым, если он не про­ходит ни через одну вершину G более одного раза.

Длиной пути или цикла называется число ребер этого пути или цикла.

Связные графы

Граф G называется связным, если для любых двух его вершин существует путь, их соединяющий. В противном случае граф G называется несвязным.

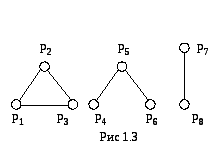
Любой несвязный граф является совокупностью связ­ных графов. Эти графы обладают тем свойством, что никакая вершина одного из них не связана путем ни с какой вершиной другого. Каждый из этих графов называется компонентой графа G. На рис. 1.3 изображен несвязный граф G с компонентами G₁,G₂,G₃. Каждая компонента являет­ся связным графом.

Деревья и лела

Связный граф, не содержащий циклов, называется деревом.

Деревом некоторого графа G называется его связный подграф без циклов. Дерево графа G, содержащее все его вершины, называется остовом графа G или его покрыва­ющим деревом.

Кодеревом T* остова Т графа G называется такой под­граф G', который содержит все его вершины и только те ребра, которые не входят в T.

Ребра остова Т называются ветвями графа G, а ребра кодерева – Т* –связями.

Граф, не содержащий циклов и состоящий из k компонент, называется к-деревом; к-дерево графа G, содержа­щее все его вершины, называется остовным.

Подграф G, содержащий все его вершины и только те ребра, которые не входят в остовное k-дерево Т графа G, называется k-кодеревом Т*.

Если граф G содержит k компонент, то его остов­ное k-дерево Т называется лесом, а k-кодерево Т* в этом случае называется КО-лесом.

Рангом графа G, имеющего n вершин и состоящего из k компонент, называется число r(G) = n - k.

Цикломатическим числом графа называется число где m –число ребер графа G.

Очевидно, что ранг и цикломатическое число связаны следующим соотношением:

Эйлеровы и гамильтоновы графы

Эйлеровым путем (циклом) графа называется путь (цикл), содержащий все ребра графа ровно один раз.

Граф, обладающий эйлеровым циклом, называется эй­леровым графом.

На рис. 1.9 граф G не является эйлеровым, так как вершина р₃ инцидентна только одному ребру.

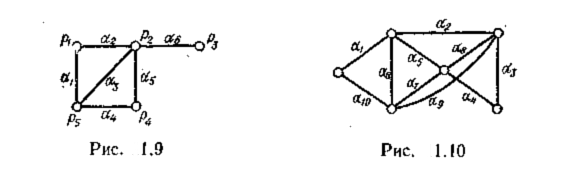
Если путь приведет в вершину p₃ то не будет ребра, по которому можно было бы выйти из p₃.

Граф G, изображенный на рис. 1.10, является эйле­ровым. Последовательность ребер, образует эйлеров цикл.

На рис. 1.9 изображен граф G, обладающий эйлеро­вым путем с концевыми вершинами p₅ и p₃.

Гамильтоновым путем (циклом) графа G называется путь (цикл), проходящий через каждую вершину G в точ­ности по одному разу

Граф, обладающий гамильтоновым циклом, называется гамильтоновым.

Критерий существования гамильтонова цикла в произ­вольном графе G еще не найден. Достаточным условием существования гамильтонова цикла является полнота графа G.

Граф, изображенный на рис. 1.9, не является гамиль­тоновым, а граф, представленный на рис. 1.11, содер­жит гамильтонов цикл

Ориентированные графы

В ориентированных графах на ребрах задано направ­ление, т. е. у каждого ребра фиксируются начало и ко­нец. Такие направленные ребра называются дугами.

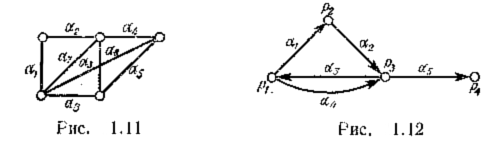
Цепью в ориентированном графе называется такая последовательность дуг, ведущих от вершины p₁ к вер­шине p_n, в которой каждые две соседних дуги имеют общую вершину и никакая дуга не встречается более одного раза. Если направление цепи совпадает с направ­лением всех принадлежащих ей дуг, то цепь называется путем.

В ориентированных графах циклом называется путь, начало и конец которого совпадают. На рис. 1.12 дуги образуют цепь, а дуги − путь. Последовательность дуг составляет цикл, а последовательность не является циклом.

Цепь, путь, цикл в произвольном графе G называются простыми, если они не проходят ни через одну свою вер­шину более одного раза. Длиной цепи, пути, цикла называется число содержа­щихся в них дуг.

Сетью называется граф, каждой дуге которого постав­лено в соответствие некоторое число (или несколько чисел).

Многие практические задачи могут быть решены е по­мощью теории графов. Рассмотрим некоторые примеры.

Задача размещения. В некотором районе имеется п населенных пунктов, соединенных друг с другом сетью шоссейных дорог. Нужно построить станцию технического обслуживания автомобилей вблизи шоссейной дороги. Рас­положение станции должно быть удобно для жителей всех населенных пунктов. Например, можно потребовать, чтобы сумма расстояний от станции до населенных пунк­тов была минимальной.

Легко представить эту задачу с помощью графа. На­селенные пункты представляются вершинами графа, а шоссейные дороги – дугами, которые их соединяют. Стан­ция технического обслуживания должна быть располо­жена на одной из дуг графа.

Задача почтальона. Почтальон ежедневно забирает письма на почте, разносит их адресатам, располагаю­щимся вдоль всего маршрута его следования, и возвра­щается обратно на почту. Путь, пройденный почтальоном, должен быть как можно короче.

Улицы представляются дугами некоторого графа. За­дача почтальона заключается в том, чтобы найти марш» рут обхода всех дуг графа минимальной длины.

Задача строительства дорог. Имеется п городов, кото­рые нужно соединить между собой новыми дорогами (не обязательно каждые два города должны быть связаны друг с другом непосредственно). Известна стоимость про­кладки дороги между любыми двумя городами. Тре­буется составить проект строительства дорог минималь­ной стоимости.

Очевидно, что каждый город представляется верши­ной графа, а дорога –дугой, соединяющей вершины. Каж­дой дуге ставится в соответствие число, равное стоимости строительства соответствующей дороги. Требуется по­строить некоторое «покрытие» графа минимальной стои­мости.

Матрицы графов

Граф может быть задан разными способами: рисунком, перечислением вершин и ребер (или дуг) и т. д. Одним из самых удобных способов является задание графа с помощью матрицы. Пусть некоторый граф G имеет n вершин p₁, p₂, ..., p_n и m ребер α₁, α₂, ..., α_m.

Построим матрицу, имеющую n строк и m столбцов. Каждая строка матрицы будет соответствовать вершине, а столбец – ребру графа. В столбце α _j все элементы, кроме двух, будут равны нулю. Для ориентированного графа в строке, соответствующей начальной вершине дуги α_j, ставят число +1, а в строке, соответствующей конечной вершине, – число -1. Для неориентированного графа в строчках матрицы, соответствующих концевым вершинам ребра α_j ставят 1, а в остальных строчках – 0. Для графов, изображенных на рис. 1.12 и 1.9, матрицы имеют соответ­ственно следующий вид:

	α1	α2	α3	α4	α5			α1	α2	α3	α4	α5	α6
p1	1	0	-1	1	0		p1	1	1	0	0	0	0
p2	-1	1	0	0	0		p2	0	1	1	0	1	1
p3	0	-1	1	-1	1		p3	0	0	0	0	0	1
p4	0	0	0	0	-1		p4	0	0	0	1	1	0
							p5	1	0	1	1	0	0

Построенные матрицы называются матрицами инциденций графа.

Матричное представление графа является наиболее удобной формой задания графа при вычислениях на машине.

Максимальные потоки в сети

Поток на графе – это совокупность однородных объек­тов, пересылаемых из одной вершины в другую по его дугам. Если вершины р и q соединены дугой α=(p, q) то поток из р в q обозначается f(p, q). Таким образом, поток – некоторая функция, заданная на дугах графа.

Пусть имеется ориентированный граф, на дугах кото­рого определена функция С(р, q). В потоковых задачах С(р, q) обычно означает пропускную способность дуги (р, q) или стоимость перевозки единицы потока по этой дуге.

Дивергенцией потока f в вершине р называется раз­ность выходящих и входящих потоков:

где A(p) – множество дуг, выходящих из вершины р, а B(p) – множество входящих в нее дуг.

Вершины, в которых , называются источниками потока f, а вершины, в которых − его стоками.

Сложим дивергенцию потока f во всех вершинах графа. Очевидно, что

Пусть задана сеть; в которой выделены две вершины s и t. Рассмотрим такие потоки f(α), что:

1) на всех дугах ;

2) при всех p, кроме, быть может, p = s и p = t.

Вершины s и t называются полюсами сети, а осталь­ные вершины называются внутренними.

Из предыдущего следует, что

Если M=0 , то поток называется циркуляцией. В против­ном случае M≠0 вершина s является источником по­тока, а вершина t – стоком. Число М > 0 называется мощностью потока f.

Задача состоит в том, чтобы найти поток f максималь­ной мощности, удовлетворяющий условиям 1 и 2.

Если рассматриваемая сеть G содержит параллельные дуги, то нужно рассмотреть новую сеть G' с теми же вершинами, что и G, в которой параллельные дуги α и β склеены. Пропускная способность полученной при этом дуги у есть . После получения решения f для сети G' оно разбивается на сумму где .

Нахождение увеличивающей цепи

Пусть заданы сеть G и какой-то поток f на этой сети. Дуги α, в которых , называются увеличивающими, так как поток через эти дуги можно увеличить на величину . Множество увеличивающих дуг обозначается .

Дуги α, в которых , называются уменьшающими, так как поток через эти дуги можно уменьшить на величину. Множество уменьшающих дуг обозначают

Заметим, что дуга а может принадлежать одновре­менно множествам и

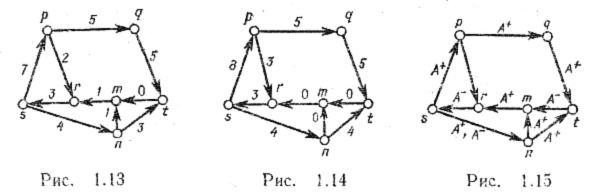
Пример. Рассмотрим сеть, изображенную на рис. 1.13, и некоторый поток f. Возьмем цепь (s, p, r, m, n, t) соединяющую вершины s и t. Вдоль этой цепи можно увеличить поток на минимальную из величин

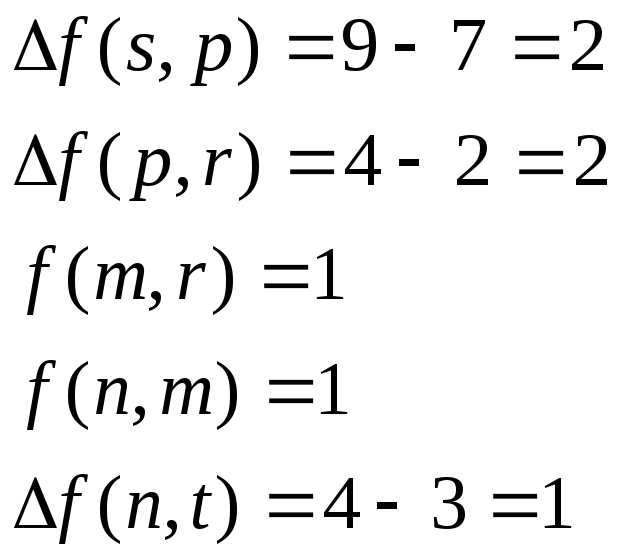
Очевидно, что мощность потока возрастет на 1 (рис. 1.14).

В общем случае вдоль некоторой цепи, соединяющей вершины s и t, можно увеличить поток, если ее прямые дуги – увеличивающие, а все обратные – уменьшающие.

Максимальный дополнительный поток δ, который можно переслать вдоль такой цепи, равен минимуму из всех для прямых дуг а и всех для обратных дуг .

Алгоритм нахождения увеличивающей цепи

1. Находят множество дуг и .

2. Отмечают вершину s (источник).

3. Далее отмечают некоторые дуги и вершины сети G. Именно: если вершина р отмечена, а вершина q – нет и дуга , то отмечают дугу α и вершину q. Если вершина р отмечена, а вершина q не отмечена и дуга , то отмечают дугу а и вершину q.

В результате получают некоторое подмножество отме­ченных вершин, соединенных отмеченными дугами. При этом, отмечая вершину q, нужно одновременно запомнить вершину р, отмеченную ранее, откуда в q привела отме­ченная дуга α (прямая или обратная).

Замечание. Приведенный алгоритм не указывает, в каком порядке нужно просматривать дуги. Например, можно сначала просмотреть все дуги, инцидентные s, отметить некоторые вершины в соответствии с правилами; затем просмотреть все дуги инцидентные отмеченным вершинам, и т. д. В другом варианте всякий раз про­сматривают дуги, инцидентные последней отмеченной вер­шине, и т. д. Этот алгоритм позволяет получить увели­чивающую цепь из s в t.

Пример. Применим алгоритм построения увеличи­вающей цепи к графу, изображенному на рис. 1.15.

Для любой отмеченной вершины будем просматривать все инцидентные ей дуги. Отмечаем источник s. Дуги (s, p), (s, n) отмечаем как выходящие увеличивающие, а дугу (r, s) – как входящую уменьшающую (рис. 1.16).

В скобках указаны вершины, соединенные с новыми вершинами отмеченными дугами. Далее просматриваем дуги, инцидентные р (рис. 1.17). Дугу (p, r) не рассматриваем, поскольку вершина r уже отмечена. Далее, просматривая дуги, инцидентные n, отмечаем дугу (n, t) и вершину t (рис. 1.18).

На этом просмотр заканчиваем, так как отмечен сток t. Идя в обратном направлении, получаем увеличиваю­щую цепь (s, n, t)

Алгоритм отыскания максимального по­тока в сети

Данный алгоритм, использующий увеличивающие цепи, называется алгоритмом Форда. Он состоит из следую­щих шагов.

1. Выбирают некоторый поток f(α) из s в t (напри­мер, f(α)=0)

2. Находят классы увеличивающих и уменьшаю­щих дуг.

Применяют алгоритм поиска увеличивающей цепи из s в t. Если такой цепи нет, то поток f – максималь­ный. Если цепь С найдена, то перейти к шагу 4.

4. Находят .

5. Пусть δ > 0 наименьшее из этих чисел.

6. Увеличивают поток вдоль цепи С на δ и пере­ ходят к шагу 2.

Очевидно, что построенный таким образом поток удов­летворяет следующим условиям:

Этот поток является максимальным. Если начальные дан­ные целочисленны, то выполнение алгоритма Форда за­вершается за конечное число шагов.

Задача о кратчайшем пути между двумя вершинами графа

Алгоритм Дейкстры

Пусть каждой дуге (х, у) графа G поставлено в соот­ветствие число , которое называется длиной этой дуги (если вершины х и у не соединены дугой, то полагают . Длина пути определяется как сумма длин отдельных дуг, составляющих этот путь. Тре­буется найти кратчайший путь между двумя заданными вершинами s и t графа G.

Алгоритм поиска кратчайшего пути В ходе выполнения алгоритма окрашивают вершины и дуги графа и вычисляют величины d(x), равные крат­чайшему пути из вершины s в вершину х, включающему только окрашенные вершины.

1. Полагают для любого. Окрашивают вершину s и полагают .

2. Для каждой неокрашенной вершины х пересчиты­ вают величину по формуле .

Если для всех вершин, то вычисления заканчи­вают. В графе G отсутствуют дуги из вершины s в не­окрашенные вершины.

В противном случае окрасить вершину х, для кото­рой величина d(x) минимальна, и дугу, ведущую в вер­шину х. Полагают у=х.

3. Если y=t, то кратчайший путь найден. В против­ном случае переходят к шагу 2.

С помощью описанного алгоритма можно определить кратчайший путь из s во все вершины исходного графа. Для этого процедуру окрашивания нужно продолжить до тех пор, пока все вершины графа не будут окрашены. При этом для графа G будет построено покрывающее дерево с корнем в вершине s (если такое дерево сущест­вует). В вершину s не ведет ни одна дуга и существует ориентированный путь из s в любую другую вершину графа.

Пример. Найти кратчайший путь между вершинами s и t для графа, изображенного на рис. 1.19

Окрасим вершину s положим для любого и . Легко найти, что ,

Окрашиваем вершину c дугу (s, с), так как вели­чина d(c) минимальна. Полагаем у=с и, поскольку вер­шина t не окрашена, снова пересчитываем величину d(x). Имеем:

Окрашиваем вершину а и дугу (s, a). Полагаем у=а и пересчитываем величины d(x). Получаем ,

Окрашиваем вершину b и дугу (a, b). Полагаем y=b, находим величины

Окрашиваем вершину d и дугу (a, d) [либо дугу (с, d)]. Полагаем y=d и находим величину d(t)=13

Окрашиваем вершину t. Кратчайшим является путь (s, b, t), Покрывающее дерево кратчайших путей изобра­жено на рис. 1.20.