3.3. Основные вычислительные процедуры в устройствах цифровой обработки сигналов и особенности их аппаратной реализации

Из анализа архитектур систем ЦОС, реализован­ных в модулярной арифметике, можно выделить следующие вычислительные процедуры, характер­ные для устройств данного типа (см. рис. 3.1, 3.2):

• прямое и обратное модулярное преобразование;

• арифметические операции модулярного умно­жения;

• арифметические операции модулярного сло­жения.

Прежде чем приступить к обсуждению методов аппаратной реализации данных процедур, необхо­димо заметить, что значения модулей для уст­ройств ЦОС в модулярной арифметике, как пра­вило, не превышают значений 2 —2 . Это связано с тем, что необходимый динамический диапазон может быть обеспечен выбором модулей в указан­ном интервале. Так, например, в работах /12, 20/ были выбраны, соответственно, наборы модулей {3,5,7, 11, 17, 64}, перекрывающий 20-битный ди­намический диапазон (так как Л=Зх5х7х х 11 х 17 х 64 = 1 256 640 > 2²⁰),и{13, 17, 19,23, 29, 31, 64}, обеспечивающий 32-битный динамический диапазон (так как M=13х7х19х х 23 х 29 х 31 х 64 = 5 556 654 272 > 2³²). Следо­вательно, нас будет интересовать, в основном, реализация модулярных сумматоров и умножите­лей небольшой, до 7—8 бит, разрядности. Данная особенность является важной, так как определяет возможные методы реализации указанных узлов.

Рассмотрим более детально принципы по­строения и особенности реализации приведенных вычислительных процедур.

3.2.1. Принципы построения модулярных сумматоров.

В общем случае можно выделить три основных подхода схемотехнической реализации модуляр­ных сумматоров (21):

• прямая логическая реализация с использовани­ем обычных блоков двоичной арифметики;

• реализация с использованием таблиц состоя­ний (так называемых look-up-tables);

• гибридный метод, т. е. использование таблиц состояний наряду с блоками двоичной арифме­тики.

Аппаратная реализация модулярных сумматоров зависит от выбранного технологического базиса. При наличии ячеек памяти могут быть примени­мы подходы, связанные с использованием таблиц состояний. Однако в случае реализации в базисе произвольной логики наиболее целесообразным с точки зрения занимаемой площади и быстродей­ствия представляется метод прямой логической реализации.

В случае прямой логической реализации сум­мирование по модулю mi для двух операндов а и b, находящихся в диапазоне {0, 1, ..., mi -1}, выпол­няется по следующей формуле:

(3.3)

Структурная схема, соответствующая формуле (3.3), приведена на рис. 3.3, а. Она состоит из обыч­ных двоичных сумматора, вычитателя и выходно­го мультиплексора, который управляется знако­вым разрядом вычитателя. Так как значение мо­дуля m определено и является константой, то при­веденную архитектуру можно видоизменить, добавив компаратор константы, который управ­ляет мультиплексором (рис. 3.3, б). Несмотря на то, что вторая структура (рис. 3.3, 6) содержит на один компонент больше (добавлен компаратор) по сравнению с первой (рис. 3.3, а), в интегральном ис­полнении обе структуры являются примерно рав­нозначными, а выбор для конкретного модуля зависит, в первую очередь, от его значения. Это объ­ясняется тем, что во втором случае может быть ис­пользован не полный, а частично-определенный вычитатель, так как нас интересуют только поло­жительные значения (а+b- ,).

Сравнение двух структур в базисе 0,5 мкм библиотеки стандартных ячеек, выполненное в работе /22/, подтверждает приведенные выводы. Кроме того, применительно ко второй структуре может быть проведена доста­точно эффективная аппаратная оптимизация для отдельных значений модулей. В работах /22, 23/ показано, что в этом случае для сумматоров по мо­дулям типа ( ) и ( ) достигается выигрыш по занимаемой площади до 25–30 % без ухудше­ния, а в отдельных случаях с улучшением быстро­действия.

Таким образом, можно видеть, что использова­ние блоков двоичной арифметики при реализации модулярных сумматоров в интегральном исполне­нии обеспечивает большую гибкость при выпол­нении требований по площади и быстродействию. Например, в выбранном базисе мо­дулярные сумматоры для небольших значений мо­дулей могут быть построены с использованием двоичных сумматоров с последовательным пере­носом в целях минимизации занимаемой площа­ди.

Для модулей большей разрядности целесооб­разно использовать двоичные сумматоры с уско­ренным переносом для обеспечения заданного быстродействия.

Стоит отметить некоторые особенности по­строения модулярных сумматоров для отдельных значений модулей. Если m_i = , то модулярный сумматор трансформируется в обычный позици­онный сумматор, в котором не используется стар­ший разряд или выходной перенос. Это связано с тем, что если (a+ b) < , то на выход модулярного сумматора должно проходить значение (a+ b) и старший разряд позиционного сумматора будет равен 0. В случае, если (а + b) > , то на выход должно проходить значение (а + b) - , а вычи­тание значения достигается путем инверсии разряда переноса, т. е. старший

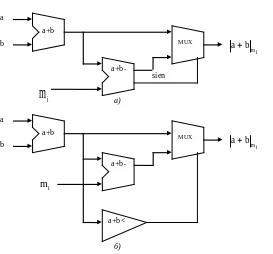
Рис. 3.3. Структура модулярного сумматора с полноразрядным вычнтатслем (а), с компаратором и неполным вычнтатслем (б)

разряд позицион­ного сумматора опять становится равным 0. Таким образом, модулярные сумматоры для значений модулей являются самыми экономичными по площади и наиболее быстродействующими.

При построении сумматоров по модулю ( ) целесообразно воспользоваться так называемым свойством изоморфизма /24/:

(3.4)

где c_out — выходной перенос или старший разряд позиционной суммы (а +b).

Формула (3.4) соответствует реализации суммато­ров с так называемым циклическим переносом из высшего разряда в низший (end-around-cany adder). То есть, если перенос c_out равен 1, то входной пе­ренос младшего разряда также равен 1 и вычисля­ется сумма (а + b+ 1), а если перенос c_out равен 0, то входной перенос младшего разряда равен 0 и вычисляется сумма (a + b). Отметим, что такой сумматор трудно реализовать напрямую с исполь­зованием обычного двоичного сумматора, так как подача выходного переноса старшего разряда c_out на входной перенос младшего разряда создает комбинационную петлю и может привести к воз­никновению автогенерации. Авторами разработа­ны методы логического синтеза указанных сумма­торов на основе BDD-технологии, которые позво­ляют реализовать быстродействующие сумматоры с ускоренным переносом по модулю ( ), уве­личивающие быстродействие в 2 и более раз.

Методы аппаратной реализации модулярных умножителей для систем ЦОС в модулярной арифметике.

Существуют различные методы реа­лизации модулярных умножителей. Некоторые из них ориентированы на определенные значения модулей типа 2" + 1 /25, 26/. В работе /27/ пред­ставлен модулярный умножитель, предназначен­ный для криптографических применений. Для зна­чений модулей разрядности более 8—10 бит могут быть использованы специальные алгоритмы по­строения модулярных умножителей /28/.

Для небольших значений модулей (до 7—8 бит), которые в основном используются в системах ЦОС в модулярной арифметике, целесообразно применять реализацию на основе индексного или дискретно-логарифмического представления опе­рандов. Основным преимуществом умножителей этого типа является тот факт, что операция моду­лярного умножения по модулю m_j заменяется опе­рацией модулярного сложения по модулю (т, — 1) с соответствующими индексными преобразова­ниями /29/.

Рассмотрим структуру индексного модулярно­го умножителя. Пусть т — значение модуля, по которому выполняется умножение двух модуляр­ных чисел , и (при этом модуль т должен быть простым числом). Отображение операции умно­жения по модулю т на операцию сложения по мо­дулю (т — 1) осуществляется по формуле

(3.5)

где g — первообразный корень, определяемый как целое число, возведение которого в степень 0, 1,2, ..., (m— 2) дает неповторяющиеся вычеты по модулю т.

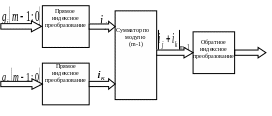
Отображение по формуле (3.5) называется изо­морфизмом между мультипликативной группой {gn} = {1,2,..., т — 1) с операцией умножения по мо­дулю т и аддитивной группой {in} = {0, 1, ..., т-2} с операцией сложения по модулю (т — 1) /30/. Структурная схема индексного модулярного ум­ножителя, соответствующего формуле (3.5), приве­дена на рис. 3.4.

Рис 3.4.

Как можно видеть из рис. 3.4, процедура модуляр­ного умножения двух чисел с использованием ин­дексного или дискретно-логарифмического пред­ставления операндов включает следующие стадии:

• нахождение индексов i_n для каждого модуляр­ного числа;

• сложение полученных индексов по модулю (т - 1);

• выполнение обратного индексного преобразо­вания.

Другим интересным способом реализации ин­дексного умножения является метод субмодуляр­ного индексного преобразования. В этом случае операция умножения по модулю т также заменяется операцией сложения по модулю (т — 1), но при этом сумматор по модулю (т — 1) расщепля­ется на несколько модулярных сумматоров с соот­ветствующим набором подмодулей msub1,..., msubr.

Этот набор должен удовлетворять следующим тре­бованиям /31/:

подмодули msub_l, ..., msub_r должны быть попа­рно взаимно простыми.

Структурная схема индексного субмодулярного умножителя приведена на рис. 3.5.

Рис. 3.5. Структурная схема параллельного индексного субмодулярного умножителя

Таким образом, процедура модулярного умно­жения двух чисел с использованием индексного субмодулярного разложения включает следующие стадии:

• нахождение прямого субмодулярного разложе­ния для набора подмодулей;

• сложение полученных элементов разложения по соответствующим подмодулям msubf,

• выполнение обратного субмодулярного преоб­разования.

Данная структура также содержит большое чис­ло компонентов, однако анализ и сравнение двух данных типов умножителей, реализованных в ин­тегральном исполнении, показывают, что индекс­ные субмодулярные умножители (см. рис. 3.5) явля­ются более эффективным решением с точки зре­ния площади и быстродействия по сравнению с обычными индексными модулярными умножите­лями (см. рис. 3.4). При этом существуют особен­ности, связанные с выбором тех значений модулей и подмодулей, которые обеспечивают лучшие ха­рактеристики качества.

Заметим, что при аппаратной реализации ин­дексных модулярного и субмодулярного умножи­телей необходимо введение дополнительной логи­ки, учитывающей условие, когда один или оба входных операнда равны нулю, и обеспечивающей нулевой результат на выходе схемы.

Проведенные авторами исследования и сравне­ния указанных архитектур индексных умножите­лей в базисе 0,5 мкм библиотеки стандартных яче­ек позволяют определить ряд критериев выбора таких значений модулей, которые обеспечивают меньшую занимаемую площадь и большее быст­родействие умножителей в заданном динамиче­ском диапазоне.

Также отметим особенности построения умно­жителей по модулю .Для указанных значений модулей результат модулярного умножения опре­деляется л младшими битами обычного позицион­ного умножения, что соответствует реализации двоичного умножителя с отбрасыванием старших разрядов.

Принципы построения прямого и обратного мо­дулярных преобразователей.

Применение аппарата модулярной арифметики оправдано при наличии эффективных средств перехода из позиционной системы счисления в модулярное представление и наоборот. Эти преобразования могут вносить зна­чительный вклад в аппаратные затраты устройства в целом.

Прямое преобразование из двоичного в моду­лярное представление может быть осуществлено с помощью прямой перекодировки и использовани­ем таблиц состояний (look-up tables). С целью уменьшения аппаратных затрат и минимизации таблиц применяется комбинированный подход, основанный на использовании таблиц состояний и модулярных сумматоров. Двоичное представле­ние «-битного числа X можно записать в виде:

(3.6)

где b, имеет значение 0 или 1.

Для вычисления значения Х по модулю т фор­мула (3.6) принимает вид

(3.7)

Структурная схема, соответствующая формуле (3.7), приведена на рис. 3.6.

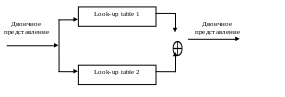
Рис. 3.6. Структурная схема преобразователя из двоичного в мо­дулярное представление

Приведенный алгоритм значительно уменьша­ет аппаратные затраты на реализацию таблиц со­стояний, а модулярные сумматоры имеют неболь­шую разрядность в соответствии с выбранным ба­зисом модулей.

Обратное восстановление числа из модулярно­го представления в двоичную систему счисления осуществляется по формуле (3.1), согласно следст­вию "Китайской теоремы об остатках". Математи­ческий алгоритм восстановления включает сле­дующие стадии:

• вычисляется произведение модулей М (М = 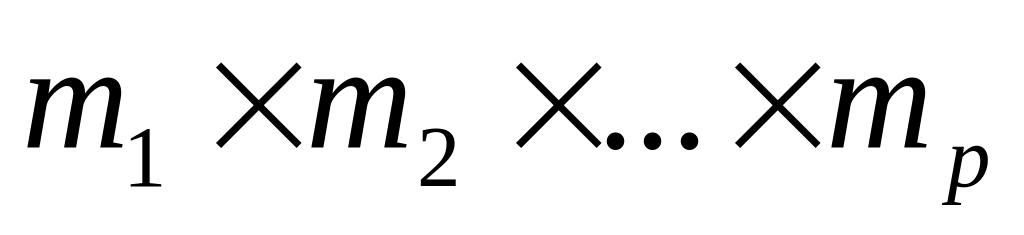); напомним, что состав­ной модуль М определяет динамический диа­пазон восстанавливаемых чисел;

• для набора модулей { } вычисля­ется набор структурных чисел (k₁, k₂, ..., к }, где k_i ;

• для набора структурных чисел вычисляются числа, обратные им, { 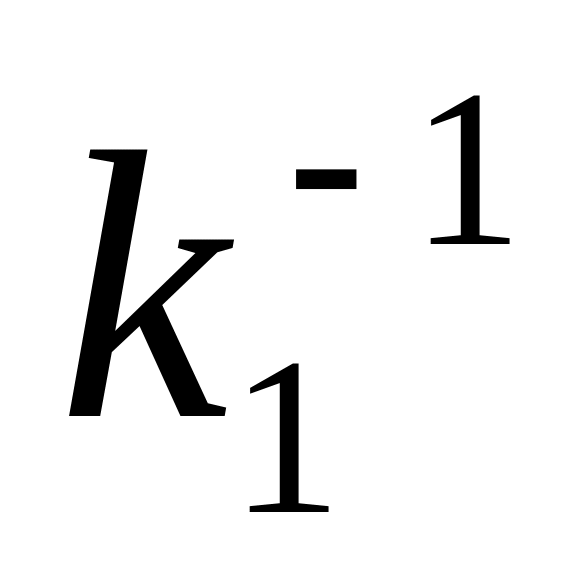, ,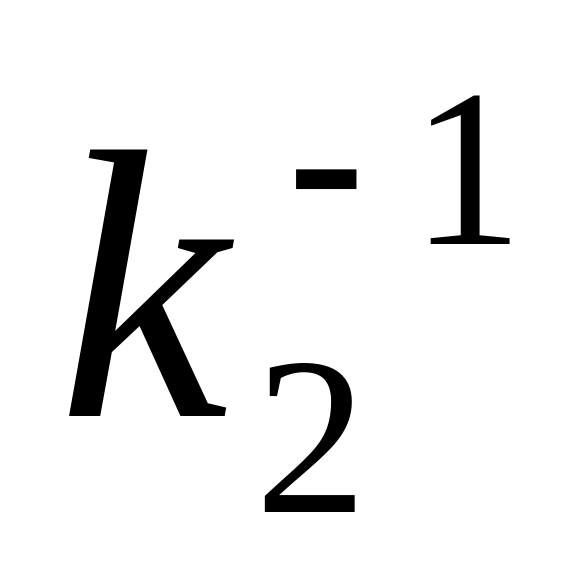… 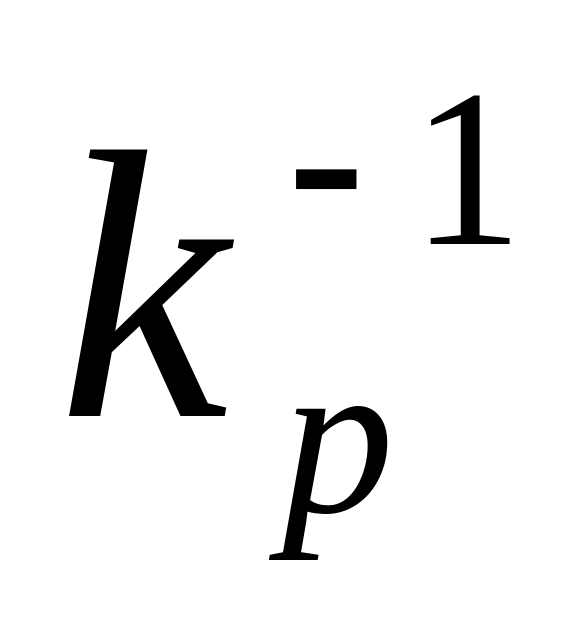}, где определяется из условия ;

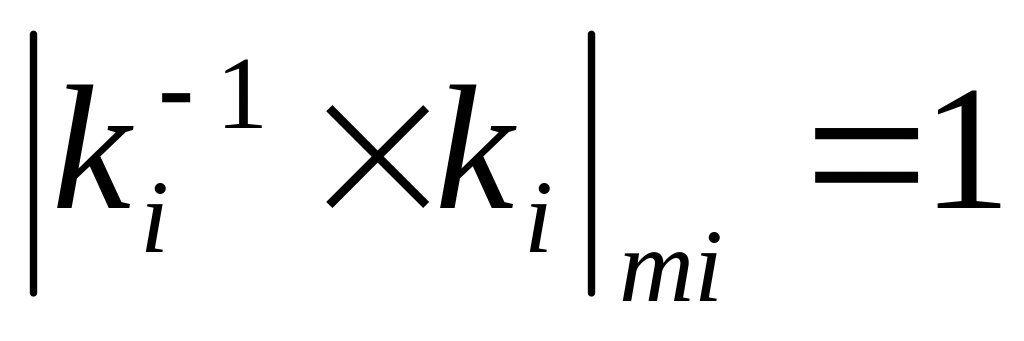• число восстанавливается по формуле (3.1). Реализация формулы (3.1) в аппаратуре также требует использования таблиц состояния наряду с модулярными сумматорами. Вариант такого пре­образователя на основе алгоритма с предваритель­ной обработкой данных, позволяющего не увели­чивать разрядность промежуточных результатов, представлен в /32/. Финальный многоразрядный сумматор по составному модулю М может быть построен на основе пирамидального сумматора с использованием сумматоров по модулю М для двух операндов.

В заключение отметим, что аппаратная реали­зация таблиц состояний (look-up tables), которые применяются во многих модулярных вычисли­тельных процедурах, зависит от выбранного бази­са, т. е. таблицы состояний могут быть реализова­ны как на основе ячеек памяти, так и на основе произвольной логики.