
- •Введение
- •1. Теория колебаний
- •1.1. Устойчивость положения равновесия
- •1.1.1. Определение устойчивости положения равновесия
- •1.1.2. Теорема Лагранжа–Дирихле
- •1.2. Колебания системы с одной степенью свободы
- •1.2.1. Собственные линейные колебания системы
- •Дифференциальное уравнение собственных линейных колебаний системы
- •Интегрирование дифференциального уравнения собственных колебаний
- •1.2.2. Влияние линейного сопротивления на малые собственные колебания системы с одной степенью свободы
- •Интегрирование дифференциального уравнения движения
- •Затухающие колебания
- •Затухающие движения
- •1.2.3. Вынужденные колебания системы без учета сопротивления
- •Основные свойства вынужденных колебаний
- •Исследование вынужденных колебаний
- •Общие свойства вынужденных колебаний
- •Основы виброзащиты
- •1.3. Математический и физический маятники
- •1.4. Малые колебания системы с двумя степенями свободы (результат для общего случая)
- •1.4.1. Кинетическая энергия
- •1.4.2. Потенциальная энергия
- •1.4.3. Диссипативная функция
- •1.4.4. Дифференциальные уравнения собственных колебаний
- •1.4.5. Интегрирование дифференциальных уравнений. Уравнение частот
- •1.4.6. Главные координаты
- •1.4.7. Влияние линейного сопротивления на собственные колебания
- •1.4.8. Вынужденные колебания без учета сопротивления
- •1.4.9. Влияние линейного сопротивления на вынужденные колебания
- •2. Теория удара
- •2.1. Основные положения и понятия теории удара
- •2.2. Теоремы об изменении количества движения и о движении центра масс для удара. Теорема Кельвина
- •2.3. Теорема об изменении кинетического момента при ударе
- •2.4. Удар точки о неподвижную поверхность
- •2.4.1. Прямой удар
- •2.4.2. Косой удар
- •2.4.3. Экспериментальное определение коэффициента восстановления
- •2.5. Теорема Карно
- •2.6. Удар двух тел
- •2.7. Центр удара
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
2.4.2. Косой удар
У
Рис. 21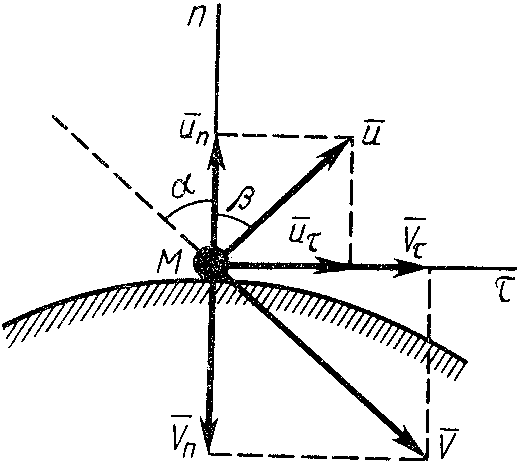
![]() имеем прямой удар. Угол
(рис. 21) называют углом падения. В общем
случае скорость точки
после удара составит с нормалью к
поверхности угол
имеем прямой удар. Угол
(рис. 21) называют углом падения. В общем
случае скорость точки
после удара составит с нормалью к
поверхности угол
![]() ,
который называют углом
отражения.
,
который называют углом
отражения.
Разложим скорости до и после удара на нормальные и касательные составляющие:
![]() ,
,
![]() .
.
Коэффициентом
восстановления
при косом ударе называют величину
![]() .
.
Применение теоремы об изменении количества движения в проекции на нормаль к поверхности приводит к выражению коэффициента восстановления через ударные импульсы
![]() ,
,
где
![]() и
и
![]() – проекции ударных импульсов на нормаль
к поверхности за вторую и первую фазы
удара.
– проекции ударных импульсов на нормаль
к поверхности за вторую и первую фазы
удара.
В
случае не идеально гладкой поверхности
![]() .
В дальнейшем принимаем, что поверхность
не обладает ударным трением и поэтому
.
В дальнейшем принимаем, что поверхность
не обладает ударным трением и поэтому
![]() .
В этом случае
.
В этом случае
![]() ,
,
![]() ,
,
![]() .
.
Эта формула выражает зависимость между углом падения и углом отражения при различных коэффициентах восстановления и отсутствии ударного трения.
2.4.3. Экспериментальное определение коэффициента восстановления
Коэффициент
восстановления можно определить
экспериментально, измеряя высоту, на
которую поднимется тело, обычно в форме
небольшого шара, после прямого удара о
поверхность (рис. 22) при падении с заданной
высоты. Если шарик падает на неподвижную
поверхность с высоты
![]() ,
то его скорость непосредственно перед
ударом
,
то его скорость непосредственно перед
ударом
![]() .
Сразу после удара скорость шарика через
высоту подъема его над поверхностью
выражается зависимостью
.
Сразу после удара скорость шарика через
высоту подъема его над поверхностью
выражается зависимостью
![]() .
Для коэффициента восстановления имеем
.
Для коэффициента восстановления имеем
![]()
 .
.
Измеряя
![]() при заданном
при заданном
![]() ,
получают значения коэффициентов
восстановления для различных материалов
шарика и поверхности.
,
получают значения коэффициентов
восстановления для различных материалов
шарика и поверхности.
М
Рис. 22
2.5. Теорема Карно
При абсолютно упругом ударе точки о неподвижную поверхность в отсутствие ударного трения скорость точки может изменяться только по направлению. Числовое значение ее остается неизменным. Кинетическая энергия точки и системы точек, находящихся в таких условиях, не изменяется за время удара. При упругом и абсолютно неупругом ударах кинетическая энергия изменяется.
Установим изменение кинетической энергии в случае абсолютно неупругого удара при мгновенном наложении связей для точки и системы в отсутствие ударного трения. По теореме об изменении количества движения для точки (рис. 23) имеем
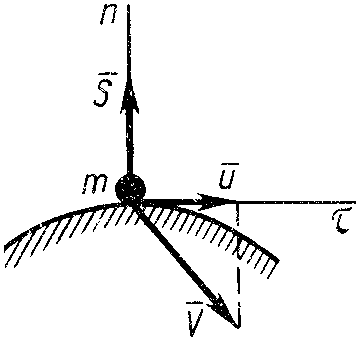 , (116)
, (116)
г
Рис. 23![]() .
В рассматриваемом случае ударный импульс
и скорость точки после удара
взаимно перпендикулярны и поэтому
удовлетворяют условию
.
В рассматриваемом случае ударный импульс
и скорость точки после удара
взаимно перпендикулярны и поэтому
удовлетворяют условию
![]() .
.
Учитывая это, умножим обе части (116) скалярно на . Получим вспомогательное соотношение
![]() . (117)
. (117)
При
абсолютно неупругом ударе кинетическая
энергия точки уменьшится на
![]() .
Добавляя в это выражение величину,
равную нулю в форме (117), получим
.
Добавляя в это выражение величину,
равную нулю в форме (117), получим
![]()
![]() .
.
Получена теорема Карно для точки о потере кинетической энергии при абсолютно неупругом ударе и отсутствии ударного трения:
![]() . (118)
. (118)
Векторную
величину
![]() называют потерянной
скоростью.
Теорему Карно для точки можно сформулировать
в следующей форме: потеря
кинетической энергии точки при абсолютно
неупругом ударе и отсутствии ударного
трения в случае мгновенного наложения
связей равна кинетической энергии от
потерянной скорости.
называют потерянной
скоростью.
Теорему Карно для точки можно сформулировать
в следующей форме: потеря
кинетической энергии точки при абсолютно
неупругом ударе и отсутствии ударного
трения в случае мгновенного наложения
связей равна кинетической энергии от
потерянной скорости.
Имея
(118) для точки, получим теорему
Карно для системы в
случае абсолютно неупругого удара и
отсутствия ударного трения. Необходимо
при этом, чтобы связи для точек системы,
испытывающих удар, создавали ударные
импульсы
![]() ,
перпендикулярные скоростям точек после
удара
,
перпендикулярные скоростям точек после
удара
![]() ,
т.е. чтобы для каждой точки выполнялось
условие
,
т.е. чтобы для каждой точки выполнялось
условие
![]() .
Тогда для каждой точки справедлива
теорема (118)
.
Тогда для каждой точки справедлива
теорема (118)
![]() , (118')
, (118')
где
![]() – потерянная скорость
-й
точки системы. Суммируя (18') по всем
точкам системы и обозначая кинетическую
энергию системы до удара
– потерянная скорость
-й
точки системы. Суммируя (18') по всем
точкам системы и обозначая кинетическую
энергию системы до удара
![]() ,
а после удара –
,
получим
,
а после удара –
,
получим
![]() ,
,
![]() ,
,
![]() . (119)
. (119)
Для справедливости теоремы Карно для системы при мгновенном наложении связей вместо условия для каждой точки достаточно выполнения менее ограничительного условия
![]() .
.
Получена теорема Карно для системы: потеря кинетической энергии при абсолютно неупругом ударе в случае мгновенного наложения связей и отсутствия ударного трения равна кинетической энергии от потерянных скоростей точек системы.
Теорему
Карно для точки и системы можно получить
также для удара, который возникает при
мгновенном снятии связей. При этом
кинетическая энергия после удара больше
кинетической энергии до удара. Потеря
кинетической энергии становится
отрицательной. Ударный импульс
при снятии связи должен быть перпендикулярен
скорости точки
![]() до удара, так как точка двигалась согласно
со связью до удара при абсолютно неупругом
ударе. Вспомогательное соотношение для
точки при снятии связей принимает форму
до удара, так как точка двигалась согласно
со связью до удара при абсолютно неупругом
ударе. Вспомогательное соотношение для
точки при снятии связей принимает форму
![]() , (117')
, (117')
а теорема Карно в этом случае имеет вид
![]() . (118'')
. (118'')
Для системы она выразится в форме
![]() . (119')
. (119')
При этом для каждой точки системы, испытывающей удар, должно выполняться условие , или .
