
- •П.Я. Бушин
- •Эконометрика
- •П.Я. Бушин
- •Эконометрика
- •Глава 2. Множественная корреляция и регрессия
- •Таблица дисперсионного анализа регрессии
- •Таблица 3.1
- •Поквартальные данные продажи учебников
- •Рис. 57. График исходных данных и тренда
- •Рис. 58. График сезонной компоненты
- •Таблица 3.2
- •Расчет прогноза с учетом сезонной компоненты
- •Рис.62. График прогноза по модели Винтера
- •Пример. Моделирование сезонной компоненты на основе фиктивных переменных
- •Как отмечалось выше (п. 2.3.4), сезонную компоненту можно моделировать и на основе фиктивных переменных. Выберем в качестве примера аддитивную модель сезонной декомпозиции и проиллюстрируем ее сходство с моделью с фиктивными переменными.
- •ОГЛАВЛЕНИЕ
- •Глава 2. Множественная корреляция и регрессия………………………………………..23

30
2.2.3. Оценки точности уравнения множественной регрессии
Как уже отмечалось, оценки параметров уравнения регрессии вычисляются по выборочным данным и лишь приближенно оценивают эти параметры. В связи с этим появляется необходимость оценить точность как уравнения регрессии в целом, так и его параметров в отдельности.
Как и в случае парной регрессии, при решении первой задачи используют процедуру дисперсионного анализа, основанную на разложении общей суммы квадратов отклонений зависимой переменной на две составляющие.
Как известно,
SST = SSR + SSE
или
|
|
|
|
|
|
|
(y y)2 |
(yˆ |
y)2 |
(y yˆ) 2 . |
|||
Аналогичное разложение имеет место и для степеней свободы:
dfT = dfR + dfE ,
где dfT = n–1 – общее число степеней свободы;
dfR = m – число степеней свободы, соответствующее регрессии (m – число независимых переменных в уравнении регрессии);
dfE = n–m–1 – число степеней свободы, соответствующее остаткам.
Разделив суммы квадратов на соответствующее число степеней свободы, получим суммы квадратов на одну степень свободы или средние квадраты, которые являются
оценками дисперсии 2 зависимой переменной y или остатков e в условиях разных предпосылок. Одна из оценок рассчитывается в предположении, что все коэффициенты в модели регрессии равны нулю (Ho: 1 = 2 =…= m =0), а другая – в общих условиях.
Затем эти оценки сравниваются по критерию Фишера с числом степеней свободы числителя, равным m и знаменателя (n–m–1). Если рассматриваемые оценки близки, то это говорит в пользу нулевой гипотезы.
Если нулевая гипотеза отклоняется, т.е. выясняется, что не все коэффициенты в модели регрессии равны нулю, то в этом случае говорят, что уравнение регрессии значимо, в противном случае – не значимо. Последнее означает, что уравнение регрессии ничего не дает для предсказания зависимой переменной и не может быть использовано в анализе.
Дисперсионный анализ множественной регрессии проводится в таблицах вида : Таблица 2.1
Таблица дисперсионного анализа регрессии
Источник |
Сумма |
|
Степени |
Средние |
|
F- |
|
вариации |
квадратов |
|
свободы |
квадраты |
отношение |
||
Модель |
SSR |
|
m |
MSR |
|
MSR |
|
Ошибки |
SSE |
|
n–m–1 |
MSE |
F= |
|
|
|
MSE |
||||||
|
|
|
|
|
|
||
Общая |
SST |
|
n–1 |
|
|
|
|
В табл. 2.1 |
MSR = SSR/m и |
MSE = SSE/(n–m–1) - оценки |
дисперсии 2 , |
||||
рассчитанные в разных условиях и сравниваемые затем на основе критерия Фишера. Вернемся еще раз к MSE. Этот показатель является одной из характеристик
точности уравнения регрессии. По-другому его называют остаточной дисперсией и
обозначают S 2 |
. MSE является несмещенной оценкой дисперсии 2 . |
ост. |
|
MSE также используется при вычислении других показателей точности уравнения регрессии. Например, корень квадратный из MSE называется стандартной ошибкой

31
оценки по регрессии (Sy,x) и показывает, какую ошибку в среднем мы будем допускать, если значение зависимой переменной будем оценивать по найденному уравнению регрессии на основе известных значений независимых переменных. Имеем
|
|
|
(y |
yˆ)2 |
|
|
|
||||
SY,X |
MSE |
|
|
|
. |
|
n m |
1 |
|||
|
|
|
|
||
Кроме того, этот показатель в неявном виде участвует в определении еще одного показателя точности уравнения множественной регрессии, а именно – коэффициента множественной детерминации (R2). Как известно,
|
R 2 |
1 |
|
SSE |
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
SST |
|
|
|
||||
|
|
|
|
|
|
|
|
||
или после преобразований: |
|
|
|
|
|
|
|
|
|
R 2 |
|
SST |
|
SSE |
|
SSR |
. |
||
|
|
|
|
|
|
|
|||
|
|
SST |
|
SST |
|||||
Отсюда следует, что коэффициент множественной детерминации показывает долю вариации результирующего показателя, обусловленную вариацией включенных в уравнение регрессии независимых переменных, или, иными словами, обусловленную регрессионной зависимостью.
Коэффициент множественной детерминации обычно выражают в процентах, поэтому, например, если R2 = 75 %, то это означает, что изменение зависимой переменной на 75 % объясняется изменением включенных в уравнение регрессии независимых переменных, а остальные 25 % изменения зависимой переменной обусловлено изменением неучтенных факторов, в том числе и ошибками.
Корень квадратный из коэффициента множественной детерминации является коэффициентом множественной корреляции:
|
|
|
|
|
R 1 |
SSE |
. |
||
|
||||
SST |
||||
|
|
|
||
Как отмечалось, коэффициент множественной корреляции показывает тесноту линейной корреляционной связи между зависимой переменной и всеми независимыми переменными. По сути дела, это коэффициент корреляции между фактическими и расчетными значениями зависимой переменной.
Коэффициент множественной детерминации изменяется от нуля до единицы и равен единице, если SSE = 0, (связь линейная функциональная), равен нулю, если SST = SSE, (линейная связь отсутствует).
Значимость коэффициента множественной детерминации определяется на основе критерия Фишера:
F |
R 2 |
(n m |
1) |
|
(1 |
R 2 ) |
m |
||
|
с m степенями свободы числителя и (n–m–1) степенями свободы знаменателя.
Из определения коэффициента множественной детерминации следует, что он будет увеличиваться при добавлении в уравнение регрессии независимых переменных, как бы слабо не были они связаны с независимой переменной. Следуя этой логике, в уравнение регрессии для увеличения точности отражения изучаемой зависимости может быть включено неоправданно много независимых переменных. Точность уравнения при этом может увеличиться незначительно, а размерность модели возрасти так, что ее анализ будет затруднен. Для преодоления этого недостатка и был разработан исправленный (на число степеней свободы) коэффициент множественной детерминации, имеющий вид:

32
|
|
R2 |
1 |
|
SSE/ (n m |
1) |
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
adj |
|
|
SST/ (n |
1) |
|
|
||
|
|
|
|
|
|
|
||||
или после преобразования: |
|
|
|
|
|
|
|
|
||
|
|
R2 |
1 |
(1 R2 ) |
n |
1 |
|
. |
||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
adj |
|
|
|
n |
m |
1 |
|
|
|
|
|
|
|
|
|
||||
Здесь |
R2 – исправленное c учетом |
степеней |
свободы значение коэффициента |
|||||||
|
adj |
|
|
|
|
|
|
|
|
|
множественной детерминации (adjusted for df). |
|
|
|
|
|
|||||
В отличие от R2 , R2 |
будет убывать, если в уравнение регрессии будут добавляться |
|||||||||
|
adj |
|
|
|
|
|
|
|
|
|
незначимые независимые переменные.
Исправленный коэффициент позволяет избежать переоценки независимой переменной при включении ее в уравнение регрессии. Если добавление переменной
приводит к увеличению Radj2 , то включение ее в уравнение регрессии оправданно, в
противном случае – нет Продолжим анализ точности уравнения регрессии. Как уже отмечалось, при
проверке значимости уравнения регрессии проверяется гипотеза о том, что все коэффициенты модели регрессии равны нулю. Если нулевая гипотеза отклоняется, то это означает, что не все коэффициенты в модели регрессии равны нулю, и тогда встает вопрос о проверке значимости каждого коэффициента регрессии в отдельности.
Такая проверка осуществляется на основе статистик Стьюдента, вычисленных для свободного члена и для коэффициентов регрессии.
Статистика Стьюдента для свободного члена и коэффициентов уравнения регрессии равна:
tbk = bk / Sbk ,
где Sbk – стандартные ошибки соответствующих оценок. Будем считать, что b0 =a, тогда
S 2 = MSE [(XTX)-1] kk , (k=0,1,…,m).
bk
Здесь [(XTX)-1] (XTX)-1 .
В случае мультиколлинеарности определитель матрицы (XTX) близок к нулю, поэтому стандартные ошибки коэффициентов регрессии существенно увеличиваются. При этом коэффициенты регрессии теряют свою познавательную ценность.
При компьютерных расчетах вместе со статистикой Стьюдента для каждой оценки параметров уравнения регрессии вычисляется и выборочный уровень значимости или р-величина. По ее значению и определяется значимость каждой оценки параметров уравнения регрессии.
2.2.4. Анализ остатков уравнения множественной регрессии на втокорреляцию
Как уже отмечалось, одной из предпосылок МНК является независимость отклонений (e = y– yˆ ) друг от друга. Если это условие нарушено, то говорят об
автокорреляции остатков. Причин возникновения автокорреляции в остатках для уравнения множественной регрессии несколько. Выделим среди них следующие:
1)в регрессионную модель не введен значимый факторный признак, и его изменение приводит к значимому изменению последовательных остаточных величин;
2)в регрессионную модель не включено несколько незначимых факторов, но их изменения совпадают по направлению и фазе, и их суммарное воздействие приводит к значимому изменению последовательных остатков;
3)не верно выбран вид конкретной зависимости между анализируемыми переменными;
33
4)автокорреляция остатков может возникнуть не в результате ошибок, допущенных при построении регрессионной модели, а вследствие особенностей внутренней структуры случайных компонент (например, при описании регрессией динамических рядов).
Анализ остатков на автокорреляцию, как и в случае парной регрессии, осуществляется обычно на основе критерия Дарбина–Уотсона. Табличные значения этого критерия определяются при известных n – объеме выборки, m - числе независимых переменных и α – уровне значимости. Дальнейшие исследования на автокорреляцию прговодятся по аналогии с простой регрессией. Если с помощью критерия Дарбина – Уотсона обнаружена существенная автокорреляция остатков, то необходимо признать наличие проблемы в правильности спецификации уравнения и либо пересмотреть набор включенных в уравнение регрессии переменных, либо изменить форму регрессионной зависимости. Но в большей степени такой анализ актуален при рассмотрении регрессии временных рядов. При анализе рядов динамики с помощью регрессии уменьшение автокорреляции в остатках может дать включение в регрессию времени, как факторной переменной.
2.2.5. |
Пошаговый выбор переменных |
|
Отбор |
переменных в уравнение множественной |
регрессии может |
осуществляться в несколько этапов. На первом этапе подобный отбор осуществляется исходя из качественного анализа изучаемого социально-экономического явления, без каких бы то ни было ограничений на переменные. На втором этапе на основе, например, анализа матрицы парных коэффициентов корреляции можно отсеять незначимые факторные переменные, если это не входит в противоречие с логикой изучаемого явления. И только на третьем этапе провести строгий отбор с использованием метода пошагового выбора переменных.
При использовании этого метода отбор переменных происходит исходя только из статистических критериев. Подобные процедуры включены во многие статистические пакеты прикладных программ и предусматривают три варианта их реализации.
Процедура “вперед” (Forward) начинает работать с “пустой” моделью и последовательно включает в модель только значимые переменные. При этом на каждом шаге значимость каждой переменной определяется заново. Осуществляется это, например, на основе коэффициентов частной корреляции и рассчитанных для них статистик Фишера. Процедура включения переменных в модель заканчивается, если на очередном шаге наибольшее значение критерия Фишера будет меньше граничного. Граничное значение либо устанавливается исследователем, либо определяется по умолчанию. Если в результате реализации этого метода переменная на каком-либо шаге была включена в уравнение, то она там остается до конечного варианта уравнения регрессии.
Процедура ”назад” (Backward) начинает работать с “полной” моделью и последовательно исключает из нее незначимые переменные. Значимость переменных здесь пересчитывается также на каждом шаге. В этом случае гарантируется, что из уравнения регрессии будут исключены только незначимые независимые переменные. Если в этой процедуре переменная на каком-либо шаге была исключена из уравнения, то она не будет включена в него до конечного варианта уравнения регрессии
Пошаговая процедура (Stepwise) включения-исключения переменных состоит в сочетании двух уже рассмотренных методов. Здесь после очередного включенияисключения переменной происходит пересчет значимости уже включенных или исключенных переменных и если какая-либо ранее включенная (исключенная) переменная оказывается незначимой (значимой), то она исключается из уравнения или включается в него.
34
В большинстве случаев эти три метода дают одинаковый конечный результат. Применение метода пошагового выбора переменных позволяет упростить уравнение регрессии без значимого ухудшения его точности. К тому же подобные процедуры исключают возможность включения в регрессию коллинеарных факторных переменных.
Пример. Множественный корреляционно-регрессионный анализ и точность МНК-оценок
Приведем пример корреляционно-регрессионного анализа многомерных наблюдений на основе следующих данных.
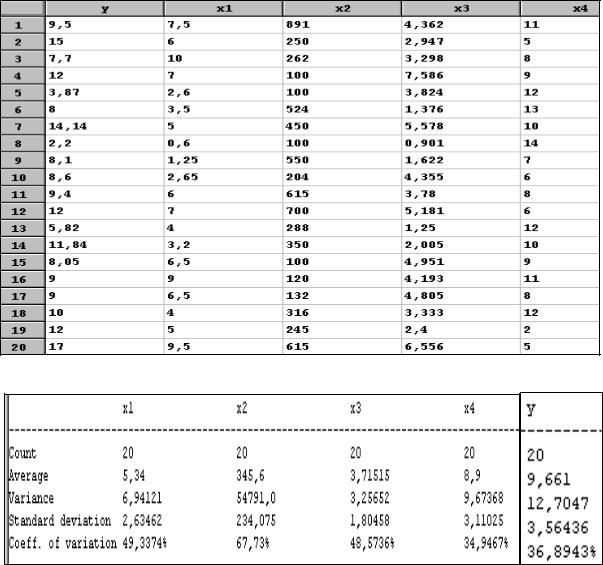
Пусть имеется информация о 20 торговых фирмах по пяти показателям: у – количество посещений в месяц (тыс. чел.); х1 – расходы на рекламу (тыс. руб.); х2 – торговые площади (м2);
х3 – число потенциальных покупателей (тыс. чел.); х4 – число конкурирующих магазинов.
Провести полный корреляционно-регрессионный анализ этой информации.
Приведем сначала для рассматриваемой информации некоторые описательные статистики (см. рис.15).
Рис. 15. Описательные статистики
35
Обратите внимание на соотношение стандартных отклонений (standard deviation) и коэффициентов вариации (coeff. of variation). Если Sx1 = 2,63 существенно меньше, чем Sx2 = 234,1 (почти в 100 раз), то Vx1 = 49,3 % меньше Vx2 = 67,7 % не на много. Связано это с тем, что исследуемые показатели имеют разные единицы измерения (тыс. чел. и тыс. руб.). В этом случае реальное представление о сравнительной мере рассеяния дает коэффициент вариации. Для одинаковых единиц измерения эти два показателя дают сходную информацию (сравните х1 и х3).
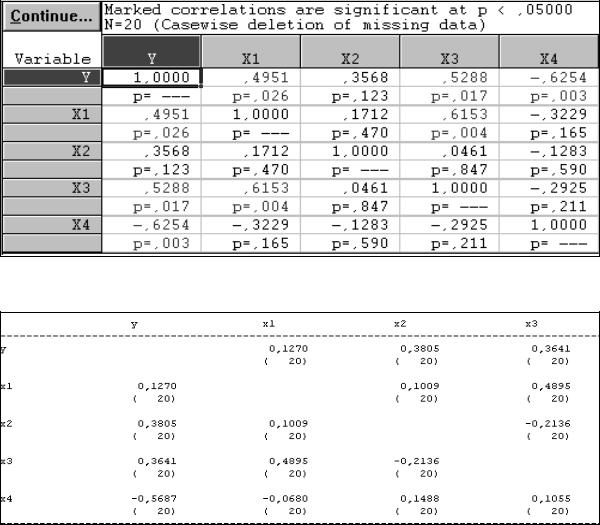
Рассчитаем для этих переменных матрицу парных коэффициентов корреляции с указанием для каждого коэффициента корреляции р-величины (см. рис. 16).
Анализ матрицы парных коэффициентов корреляции показывает, что:
1)значимыми являются три переменные: х1, х3 и х4 (для них расчетные уровни значимости меньше 0,05) – это следует из анализа строки (столбца) коэффициентов для зависимой переменной y;
2)мультиколлинеарность отсутствует (наибольший коэффициент корреляции
между независимыми переменными rx1 x3 = 0,61, что меньше 0,8).
Рис.16. Матрица коэффициентов корреляции (ППП STATISTICA)
Матрица частных коэффициентов корреляции следующая (см. рис.17) (столбец х4 отсутствует, но в силу симметрии этой матрицы его можно заменить строкой х4):
Рис. 17. Матрица частных коэффициентов корреляции (ППП Statgraphics)
Как видим, чистая связь между у и х1 ослабла, а между у и х3, наоборот – усилилась. Теснота других связей существенно не изменилась.
Приведем результаты расчетов по регрессионному анализу (рис.18 – 20).

36
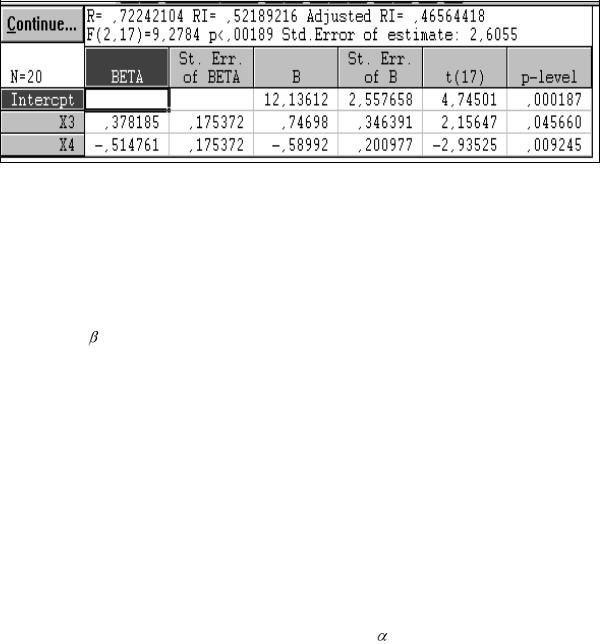
Рис. 18. Отчет об уравнении регрессии (ППП STATISTICA)
Рис. 19. Тот же отчет для ППП Statgraphics
Рис. 20. Тот же отчет в электронной таблице Excel
Окно отчета в ППП Statgraphics (рис. 19) приводит полную информацию о регрессии, а в ППП STATISTICA (рис. 18) дисперсионный анализ регрессии и коэффициент Дарбина – Уотсона приводятся в отдельных окнах. Кроме того, в ППП

37
STATISTICA рассчитываются - коэффициенты, чего нет в ППП Statgraphics. Отчет в Excel (рис. 20), кроме всего, дает еще и доверительные интервалы для параметров регрессии, но здесь нет - коэффициентов и статистики Дарбина – Уотсона, а также
пошаговой регрессии.
Различные отчеты здесь приведены для их сравнительного анализа. Дисперсионный анализ регрессии показывает, что уравнение регрессии значимо (р-
величина статистики Фишера меньше 0,05).
Коэффициенты множественной корреляции (R = 0,777) и множественной детерминации (R2 = 0,604) показывают, что уравнение регрессии довольно точно описывает зависимость y от остальных переменных (на 60,4 % изменение y обусловлено изменением всех других переменных).
Различия в исходном и исправленном коэффициентах множественной детерминации ( Radj2 = 0,5) говорит о том, что в уравнении регрессии есть незначимые
переменные. На это же указывают расчетные уровни значимости оценок коэффициентов уравнения регрессии. Среди них только один (при х4) имеет p-value или p-level меньше 0,05. Поэтому, если судить формально на основе этих показателей, то на количество посещений в месяц магазинов фирмы значимо влияет только число конкурирующих магазинов. Хотя пошаговый регрессионный анализ дает иные результаты, о чем речь ниже.
О значимости коэффициентов уравнения регрессии можно судить также и по доверительным интервалам, построенным для них. Если такой доверительный интервал содержит нуль, то это означает, что коэффициент при соответствующей переменной равен нулю. Просмотрите доверительные интервалы для коэффициентов уравнения регрессии по отчету в Excel и убедитесь в правильности высказанного предложения.
Сравнивая коэффициенты регрессии в натуральном масштабе и стандартизованные ( - коэффициенты), видим, что они несут разную информацию, и если мы хотим сделать верные выводы о степени влияния факторных признаков на изучаемый показатель, то судить об этом надо по -коэффициентам (см. отчет об уравнении регрессии в ППП Statistica). Судя по -коэффициентам (столбец ВЕТА), делаем вывод,
что наименьшее влияние на количество посещений в месяц магазинов фирмы имеет переменная х1 – расходы на рекламу, а наибольшее – переменная х4 – число конкурирующих магазинов. Коэффициенты в натуральном масштабе в данном случае сравнивать нельзя, т. к. единицы их измерения разные.
Коэффициент Дарбина – Уотсона равен 2,43 (см. рис. 19), а его уровень значимости больше 0,05, что говорит о наличии проблемы в спецификации уравнения регрессии. Воспользуемся табличными значениями этого критерия. При n = 20, m = 4 и  = 0,05 имеем (см. табл. в приложении): dl = 0,9, du = 1,83. Тогда процедура принятия решения следующая:
= 0,05 имеем (см. табл. в приложении): dl = 0,9, du = 1,83. Тогда процедура принятия решения следующая:
__есть__ dl ___?____ du _нет_4-du ___?_____4-dl __есть___
0 0,9 1,83 2,17 3,1 4
Итак, вычисленное значение статистики Дарбина – Уотсона попало в область неопределенности (между 2,17 и 3,1), поэтому на основе этого правила нет статистических оснований ни принять ни отклонить гипотезу о наличии автокорреляции в остатках.
В то же время 2,43 меньше, чем 2,5, поэтому эмпирическая рекомендация (если значение критерия между 1,5 и 2,5, то автокорреляция отсутствует) не подтвердила факта отсутствия автокорреляции. Так что этой рекомендацией надо пользоваться осторожно (как предварительный вывод).
38
Проведем теперь отчет о пошаговом регрессионном анализе. Его результаты приведены на рис. 21.
Рис. 21. Отчет о пошаговой регрессии после исключения незначимых переменных
(ППП STATISTICA)
Как видим, коэффициент множественной детерминации изменился не значимо (был равен 60,4 %, а стал равен 52,2 %). Но уравнение регрессии при этом стало существенно проще – вместо четырех содержит всего две переменные.
Кроме того, вместо трех значимых переменных (такой вывод мы сделали анализируя матрицу парных коэффициентов корреляции) их стало две: х3 и х4, т. е. окончательно имеем, что на количество посещений магазинов фирмы значимо влияют только число потенциальных покупателей и число конкурирующих магазинов и если судить по -коэффициентам, то в большей мере влияет число потенциальных
покупателей. Разные знаки при этих коэффициентах говорят о разной направленности таких влияний. А поскольку коэффициент парной корреляции между этими показателями равен нулю (см. для него p-value на рис. 16), то эти переменные линейно независимы и мы можем провести их интерпретацию.
Коэффициент при х3, т. е. b3 равен 0,747, следовательно, изменение числа потенциальных покупателей на 1 тыс. приведет в среднем к изменению числа посещений магазинов фирмы на 747 человек (уменьшит при уменьшении и увеличит при увеличении). Коэффициент при х4, т. е. b4 равен (–0,59), следовательно, изменение числа конкурирующих магазинов на единицу приведет в среднем к изменению числа посещений магазинов фирмы на 590 человек. При этом надо иметь в виду, что на основе имеющейся информации мы сумели описать с помощью этого уравнения изменение числа посещений магазинов фирмы только на 52,2 %. Остальные 47,8 % изменения числа посещений магазинов фирмы зависят от неучтенных в регрессии факторов, в том числе от ошибок наблюдений.
Коэффициент Дарбина–Уотсона для этого уравнения равен 2,33, а табличные
значения равны dl = 1,1; du = 1,54 (см. приложения при |
= 0,05, n = 20, m = 2). Имеем: |
||||
___есть__ dl ___?__ du ___нет___4-du ___?__4-dl __есть___ |
|||||
0 |
1,1 |
1,54 |
2,46 |
2,9 |
4 |
Вычисленное значение d = 2,33 находится между 1,54 и 2,46, следовательно, для этого уравнения автокорреляция остатков отсутствует.
2.3. Особые случаи использования МНК во множественной регрессии 2.3.1. Оценка параметров уравнения множественной регрессии в условиях
мультиколлинеарности (пошаговый регрессионный анализ)
Как уже отмечалось, одной из предпосылок МНК является отсутствие полной мультиколлинеарности между факторными переменными. В противном случае теряется смысл коэффициентов уравнения регрессии и их оценки не точны.
Проиллюстрируем это на следующем примере:
39
Пример. Мультиколлинеарность и пошаговая регрессия
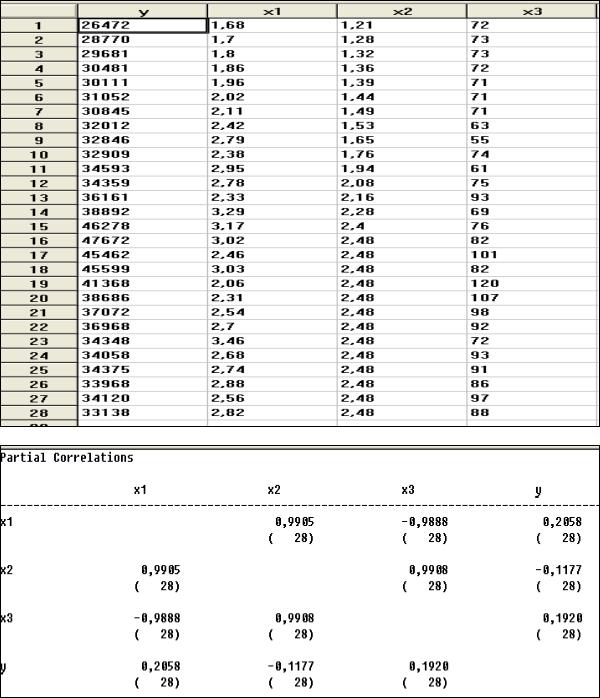
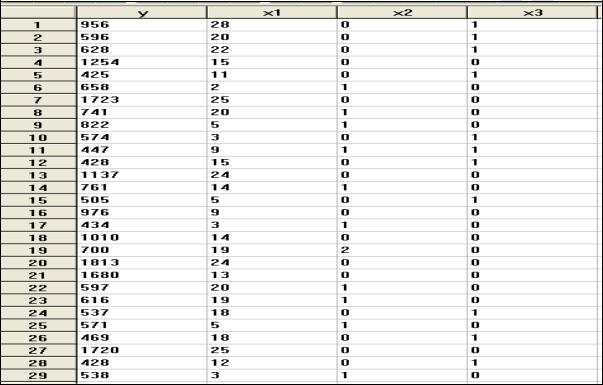
Пусть имеется следующая информация о количестве владельцев акций (у) в зависимости от цены акции (х1), дивидендов на одну акцию (х2) и отношения дохода к цене (х3) за последние 28 периодов:
Рис. 22. Матрица частных коэффициентов корреляции Матрица частных коэффициентов корреляции (см. рис. 22) свидетельствует о
наличии полной мультиколлинеарности.
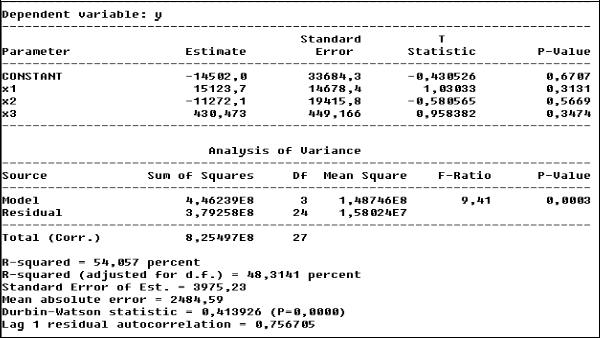
Приведем результаты регрессионного анализа этой информации. Уравнение регрессии приведено на рис. 23. Проанализируем его.
40
Рис. 23. Отчет о множественной регрессии Критерий Фишера показывает, что данное уравнение регрессии значимо (р-
величина для него меньше 0,05). Это означает, что гипотеза о равенстве нулю одновременно всех коэффициентов регрессии отклоняется. В то же время анализ значимости каждого коэффициента в отдельности показывает, что все они равны нулю (все р-величины для них больше 0,05). Этот факт подтверждает проблематичность использования классического регрессионного анализа в случае нарушения предпосылки об отсутствии мультиколлинеарности факторных переменны. Как отмечалось, в этом случае ошибки оценок коэффициентов регрессии становятся значительными по величине (в нашем примере они сопоставимы с самими оценками) и это приводит к неоправданно малым значениям t-статистик для этих коэффициентов и к неоправданным выводам о незначимости этих коэффициентов.
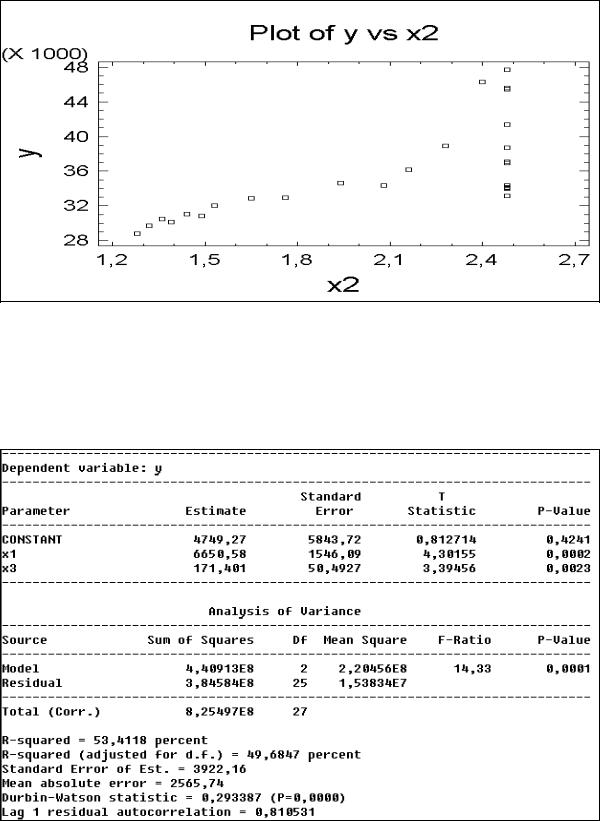
При попытке интерпретации коэффициентов этого уравнения получим «странные» выводы, а именно: при увеличении на единицу цены одной акции число владельцев акций увеличится на 15 123, а при увеличении дивидендов на одну акцию число владельцев акций уменьшится на 11 272 (при среднем числе держателей акций, равном 35 770). Как видно из нижеприведенного графика (рис. 24), диаграмма рассеяния для переменных у и х2 показывает рост числа владельцев акций при росте дивидендов, а отрицательный коэффициент при переменной х2 в уравнении регрессии (рис. 23) «говорит» об обратном.
41
Рис. 24. Диаграмма рассеяния для переменных у и х2 Это лишний раз подтверждает тот факт, что в случае мультиколлинеарности смысл
коэффициентов уравнения регрессии теряется.
Другие проблемы в связи с этим уравнением мы здесь не обсуждаем (например, наличие автокорреляции в остатках или выполнение предпосылки МНК об их гомоскедастичности). Об этом речь ниже. Приведем результат пошаговой регрессии (рис. 25), как иллюстрацию одного из методов избавления от мультиколлинеарности путем удаления из уравнения регрессии одной из коллинеарных переменных.
Рис. 25. Отчет о пошаговой регрессии Как видим, при исключении переменной х3 оставшиеся две переменные стали
значимыми. Это не означает, что раньше они были незначимыми. Просто ошибки оценок этих коэффициентов при удалении коллинеарной переменной значительно уменьшились (сравните ошибки оценок коэффициентов уравнений до и после
42
исключения этой переменной). Да и сами коэффициенты (вернее их оценки) стали иными и в большей мере отражают реалии.
Точность же упрощенного уравнения регрессии значительно не изменилась, а исправленный коэффициент множественной детерминации даже увеличился (см. рис. 23 и 25). Последний факт подтверждает свойство исправленного коэффициента множественной детерминации уменьшаться при включении в уравнение регрессии незначимой факторной переменной.
Отметим, что проблема автокорреляции остатков здесь осталась. Для ее решения здесь нужны специальные приемы, о чем речь ниже.
2.3.2. Оценка параметров уравнения множественной регрессии с автокоррелированными остатками
Пусть рассматривается уравнение простой регрессии yi = a + bxi + ei, в котором остатки ei не удовлетворяют 3-й предпосылке МНК, т. е. в них наблюдается автокорреляция. Будем считать, что это автокорреляция первого порядка, т. е. наблюдается зависимость между остатками вида: ei = ra1ei-1 + ui. В этой зависимости коэффициент ra1 является коэффициентом корреляции между соседними членами ряда. При этом предполагается, что при перекрестной информации наблюдения упорядочены по величине анализируемого показателя. Остатки ui = ei – ra1ei-1 в этом случае уже не зависят друг от друга. Запишем исходное уравнение для индекса i-1:
yi-1 = a + bxi-1 + ei-1,
умножим его на ra1 и вычтем из исходного уравнения. Получим:
yi – ra1 yi-1 = a(1– ra1) + b(xi – ra1 xi-1) + (ei – ra1ei-1)
или
yi* = a* + b xi* + ui.
В последнем уравнении остатки уже не зависимы.
Такое преобразование называется авторегрессионным преобразованием первого порядка, а метод – двухшаговой процедурой Дарбина. Оценив параметры полученного уравнения обычным МНК, получим эффективные оценки исходного уравнения. Такое преобразование рекомендуется применять в случае, если коэффициент Дарбина – Уотсона близок к 1 и известен коэффициент автокорреляции ra1.
Если коэффициент автокорреляции неизвестен, тогда применяется процедура Кохрейна – Оркатта. Это итерационная процедура. На первом шаге обычным МНК получают оценки исходного уравнения и на их основе вычисляются остатки, которые затем участвуют в расчете первого приближения коэффициента автокорреляции первого порядка (ra1) из соотношения ei = ra1ei-1 + ui. Оценив ra1, используем его в автокорреляционном преобразовании для получения преобразованного уравнения yi* = a* + b xi* + ui. Оценив параметры этого уравнения, рассчитываем для него остатки, которые затем снова используются для получения преобразованного уравнения и т. д. Этот процесс продолжается до тех пор, пока на очередной итерации коэффициент ra1 либо не изменится, либо изменится мало (на величину допустимой точности). Рассчитанное таким образом уравнение затем используется для получения эффективных оценок исходного уравнения. Этот метод и носит название процедуры Кохрейна-Оркатта по имени ее авторов.
Пример. Применение двухшагового автокорреляционного преобразования и процедуры Кохрейна – Оркатта для устранения автокорреляции остатков
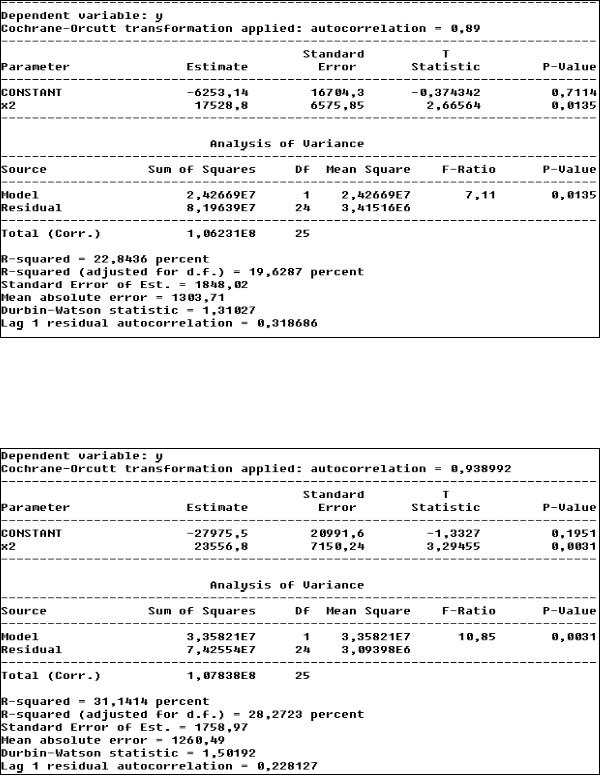
Если для ранее рассмотренного примера формально применить двухшаговую автокорреляционную процедуру с коэффициентом автокорреляции первого порядка, равным 0,89 (он получается таким, если оценить автокорреляцию по уравнению ei = ra*ei-1 + ui), то после удаления незначимых переменных получим (см. рис. 26)
43
Рис. 26. Уравнение регрессии после использования двухшаговой процедуры Дарбина и пошаговой процедуры исключения незначимых переменных
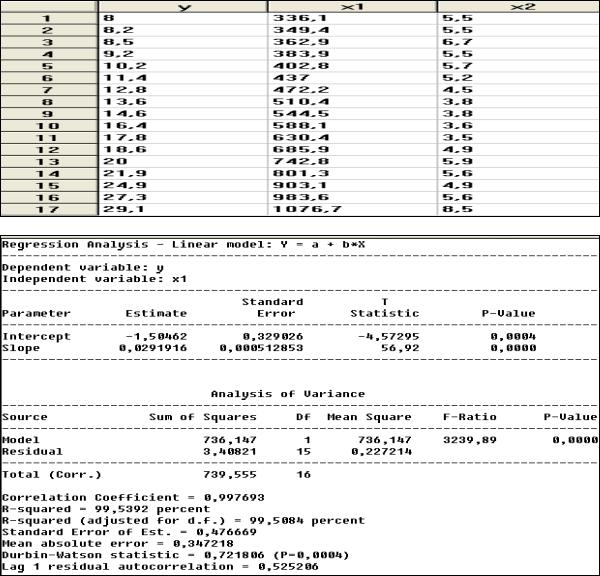
В данном случае уравнение получилось с одной значимой переменной и низкой общей значимостью (R2 = 23 %), хотя проблема автокорреляции остатков ослабла. Применив оптимизационную процедуру Кохрейна – Оркатта, получим следующее уравнение (см. рис. 27):
Рис. 27. Уравнение регрессии после применения метода Кохрейна – Оркатта и пошаговой процедуры исключения незначимых переменных
Проблема с автокорреляцией еще более ослабла, да и уравнение стало более точным, но вряд ли можно заплатить такую чрезмерную цену за решение проблемы автокорреляции остатков (значительная потеря точности уравнения регрессии и потеря значимой переменной).
44
Следует отметить, что подобный негативный результат использования описанных методов не закономерность, а, скорее, исключение. Есть много примеров удачного использования таких методов, в том числе один из них приведен ниже.
Подобным преобразованиям подвергаются переменные и в случае множественной регрессии.
Пример. Оценка параметров уравнения множественной регрессии с автокоррелированными остатками из-за ошибки в спецификации уравнения регрессии
Рассмотрим случай ошибочного выбора набора объясняющих переменных. В этом случае избавление от автокорреляции в остатках добиваются путем добавления в уравнение регрессии дополнительной переменной.
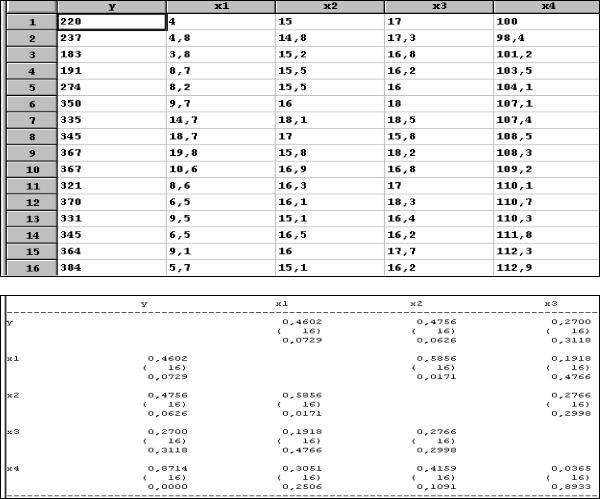
Пусть имеется информация об объемах продаж по некоторому региону (у), а также о доходах населения этого региона (х1) и проценте безработных в регионе (х2) за последние 17 периодов:
Рассчитаем сначала уравнение зависимости продаж от доходов (рис. 28):
Рис. 28. Отчет о простой регрессии Как видим, уравнение регрессии довольно точно описывает эту зависимость:
коэффициент детерминации равен 99,8 %. Но коэффициент Дарбина – Уотсона, равный 0,72, и его уровень значимости, равный нулю, говорят о наличии автокорреляции в

45
остатках, что подтверждается также и графиком остатков (см рис. 29). Их значения явно не случайны:
Рис. 29. График остатков для простой регрессии Добавим теперь в уравнение регрессии факторную переменную х2 – процент
безработных. Получим:
Рис. 30. Отчет о множественной регрессии Добавление еще одной переменной в уравнение регрессии его точность не изменило
(уравнение и так было точным), но зато после этого автокорреляция остатков исчезла (коэффициент Дарбина – Уотсона стал равен почти двум).
Рассмотренные выше два примера иллюстрируют факт, что решение проблемы автокорреляции остатков не однозначно. В одних случаях это достигается просто, в других – сложнее.
Заметим, что в обоих случаях мы применяли регрессионный анализ к временным рядам.
2.3.3. Оценка уравнения множественной регрессии с гетероскедастичными остатками (обобщенный МНК)
Проиллюстрируем использование частного случая обобщенного МНК для оценки уравнения регрессии в случае гетероскедастичности остатков.
Вернемся к уравнению регрессии на рис. 28. После проведения пошаговой регрессии нам удалось в какой-то мере избавиться от проблемы мультиколлинеарности, но в остатках этого уравнения присутствует автокорреляция (коэффициент Дарбина – Уотсона равен 0,72 и р-величина для него меньше 0,05) и, кроме того, остатки гетероскедастичны. Применим обобщенный МНК для избавления
46
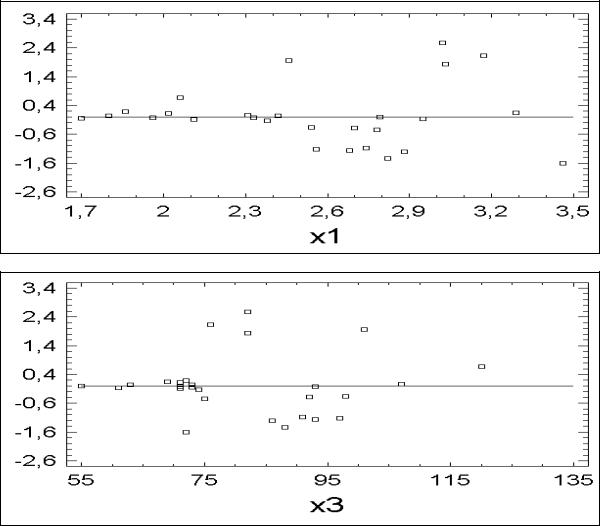
от гетероскедастичности остатков. Для этого проанализируем поведение остатков в зависимости от включенных в регрессию переменных (рис. 31 и 32).
Рис. 31 График остатков против значений переменной х1
Рис. 32 График остатков против значений переменной х3 Как видно из приведенных графиков, остатки в большей степени зависят от
значений х1, чем х3. Примем факт гетероскедастичности остатков без тестирования их по Голдфелду – Квандту и применим обобщенный МНК в виде его частного случая – взвешенного МНК, приняв за веса значения переменной х1.
Итак, вместо уравнения регрессии y = a + b1*x1 + b2*x3 + e будем оценивать уравнение в виде y/x1 = a/x1 + b1 + b2*/x1 + e/x1.
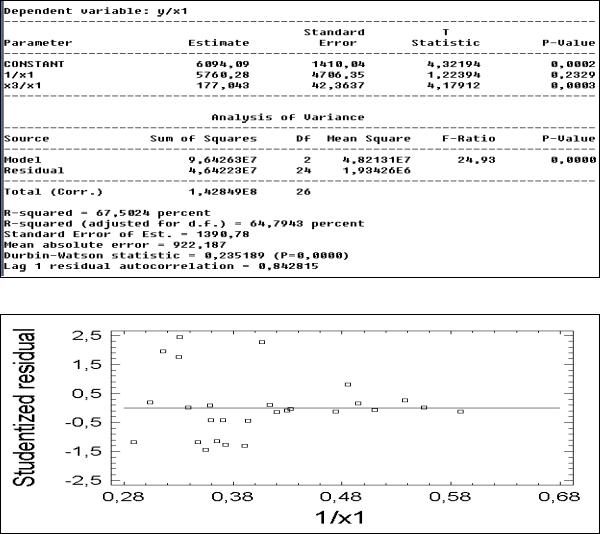
Оцененное уравнение имеет вид (рис. 33)
47
Рис. 33. Отчет об обобщенном МНК (с весами)
Проанализируем остатки против значений переменной 1/х1 (рис. 34).
Рис. 34. График остатков против значений преобразованной переменной 1/х1 Как видим, картина гетероскедастичности сменилась на противоположную, если
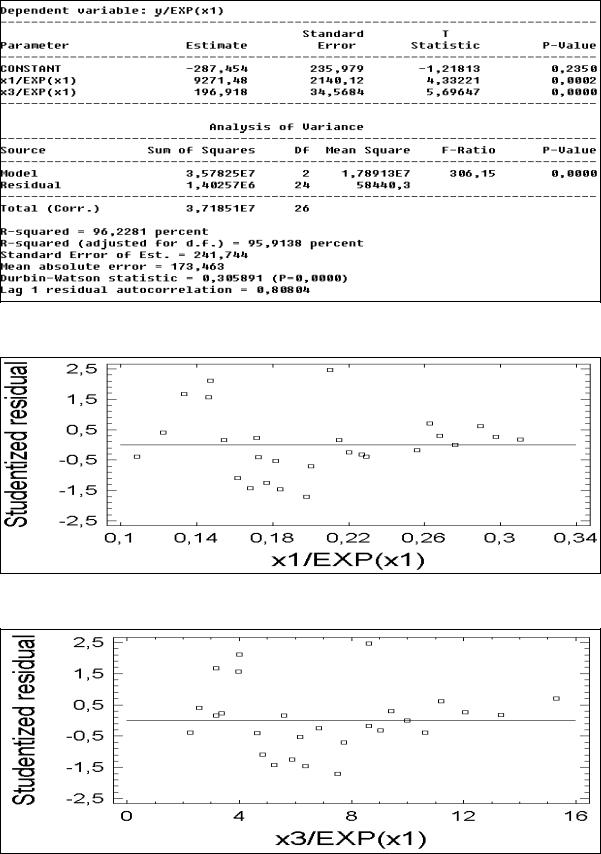
раньше с ростом х1 росла и дисперсия остатков, то теперь с ростом 1/х1 дисперсия остатков убывает. Тем не менее гетероскедастичность осталась. Попробуем уменьшить этот эффект, взяв вместо х1 ее экспоненту. Получили (рис. 35), что уравнение регрессии стало значительно точнее. Коэффициент детерминации увеличился с 67,5% до 96,2%. Обе переменные в этом уравнении стали значимыми. К тому же, остатки стали удовлетворять свойству гомоскедастичности (см. рис. 36 и 37).
48
Рис.35. Преобразованное уравнение регрессии
Рис. 36. График остатков против 1/ех1 для преобразованного уравнения
Рис. 37. График остатков против х3/ех1 для преобразованного уравнения
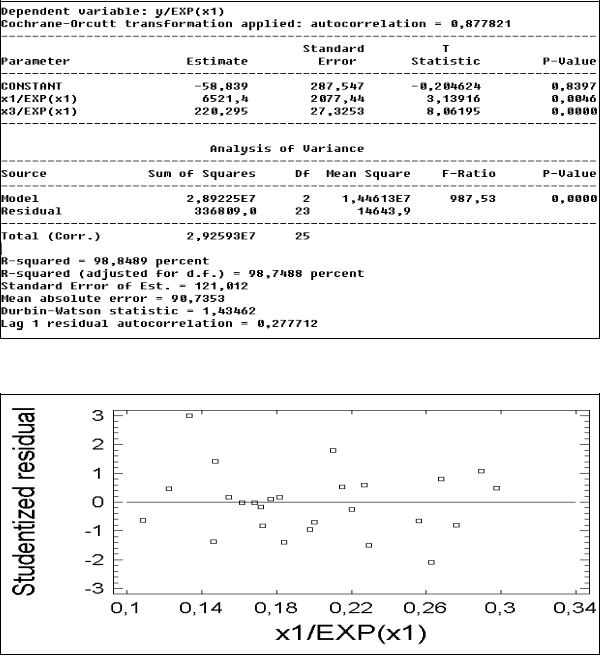
Но автокорреляция в остатках осталась (статистика Дарбина – Уотсона равен 0,3). Применим к последнему уравнению преобразование Кохрейна – Оркатта (рис. 38):
49
Рис. 38. Уравнение регрессии после применения процедуры Кохрейна – Оркатта Статистика Дарбина – Уотсона стала равна 1,43 и поведение остатков в этом
уравнении существенно не изменилось (рис. 39).
Рис. 39. График остатков после применения процедуры Кохрейна – Оркатта В итоге получили уравнение регрессии, для которого выполняются предпосылки
МНК о гомоскедастичности остатков и об их независимости друг от друга. К тому же процедура Кохрейна – Оркатта повысила точность уравнения (сравните значения коэффициентов множественной детерминации).
Итак, вместо уравнения y = a + b1*x1 + b2*x3 + e оценили уравнение в виде y/еx1 = a + b1 х1/ех1+ b2*х3/еx1 + e`.
О смысле коэффициентов этого уравнения говорить сложно, поскольку переменные подверглись сложному преобразованию. Здесь приведены формальные преобразования, призванные проиллюстрировать принципиальную возможность использования описанных ранее процедур для обеспечения выполнимости предпосылок МНК.
50
Задания для самостоятельной работы Задание 1
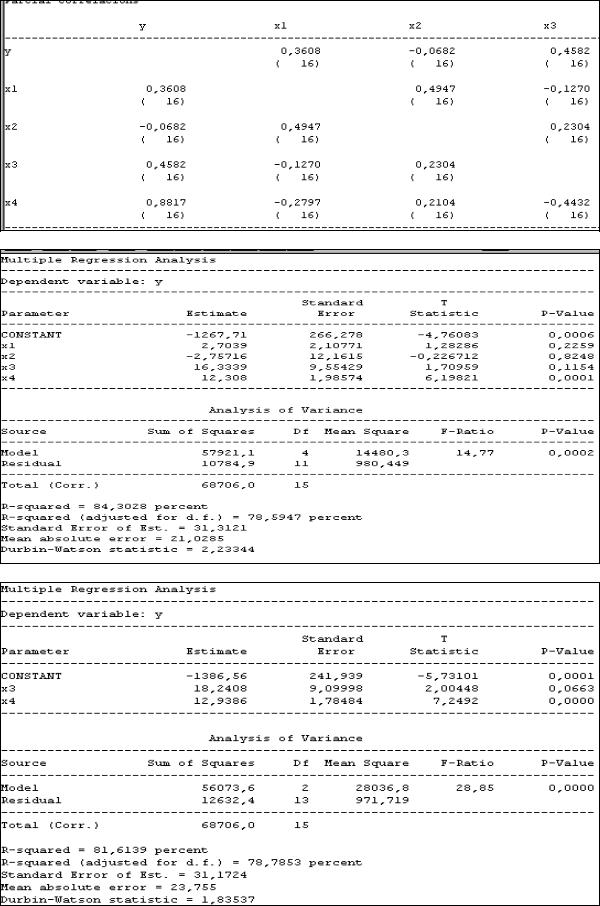
Имеется информация о результатах работы 16 фирм по следующим показателям
(см. рис. 40):
у – объем реализации (млн руб.); х1 – расходы на рекламу (млн руб.); х2 – цена собственной продукции;
х3 – цена продукции фирмы-конкурента; х4 – инвестиции (в процентах к предыдущему году).
Провести корреляционно-регрессионный анализ этой информации в соответствии с рассмотренным примером. Для этого:
1). Проанализировать матрицу парных коэффициентов корреляции (см. рис. 41).
2). Проанализировать в сравнительном анализе с предыдущей матрицей матрицу частных коэффициентов корреляции (см. рис. 42).
3). Проанализировать точность уравнения регрессии (см. рис. 43).
4). Проанализировать точность уравнения пошаговой регрессии (см. рис. 44) и проинтерпретировать его коэффициенты.
5). Основываясь на отчете о пошаговой регрессии в ППП STATISTICA (рис. 45), проведите сравнительный анализ степени влияния оставшихся в регрессии переменных на зависимую переменную по коэффициентам регрессии в натуральном масштабе и по стандартизованным коэффициентам регрессии. Поясните результаты анализа исходя из смысла этих коэффициентов.
Рис. 40. Исходная информация
Рис. 41. Матрица парных коэффициентов корреляции
51
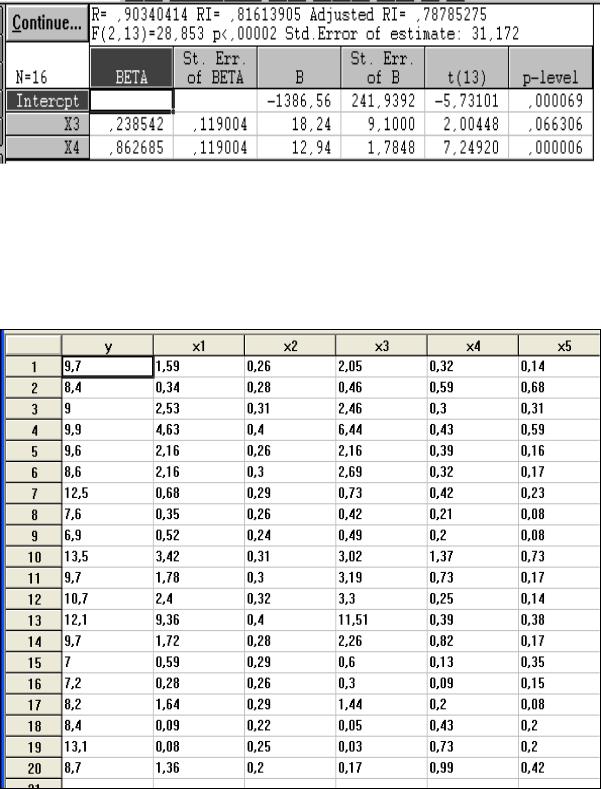
Рис. 42. Матрица частных коэффициентов корреляции
Рис. 43. Отчет о полном уравнении регрессии
Рис. 44. Отчет о пошаговой регрессии в ППП Statgraphics
52
Рис. 45. Отчет о пошаговой регрессии (ППП STATISTICA)
Задание 2
Имеется информация о 20 сельскохозяйственных районов по следующим данным: у – урожайность зерновых культур (ц/га); х1 – число тракторов (приведенной мощности) на 100 га;
х2 – число зерноуборочных комбайнов на 100 га; х3 – число орудий поверхностной обработки почвы на 100 га;
х4 – количество удобрений, расходуемых на га (т/га); х5 – количество химических средств защиты растений (ц/га).
Провести полный корреляционно-регрессионный анализ этой информации, включая пошаговый анализ и анализ остатков. По графику остатков выделите нетипичные районы и определите, в чем их отличие от остальных.
Задание 3
Провести полный корреляционно-регрессионный анализ следующей информации по магазину для 30 продавцов:
sales – объем продаж за месяц;
53
test1 – результаты теста на способность; age – возраст;
test2 – результаты теста на тревожность; expjob – опыт работы;
avball – средний балл школьного аттестата.
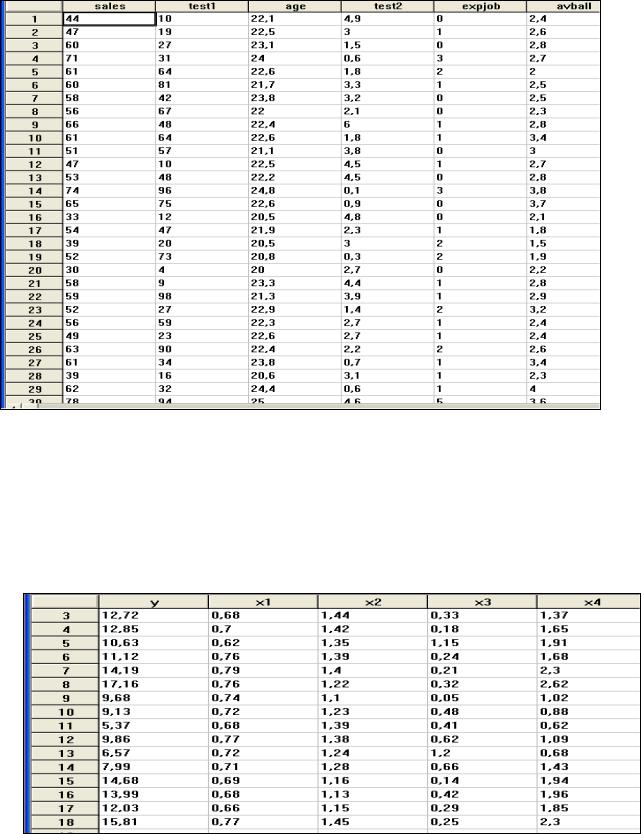
Задание 4
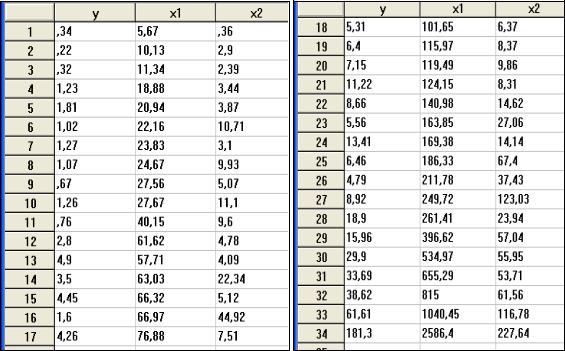
Провести полный корреляционно-регрессионный анализ информации по 18 предприятиям, характеризующимися следующими технико-экономическими показателями:
у – рентабельность (%); х1 – удельный вес рабочих в составе промышленно-производственного персонала;
х2 – коэффициент сменности оборудования; х3 – удельный вес потерь от брака; х3 – фондоотдача.
54
Задание 5
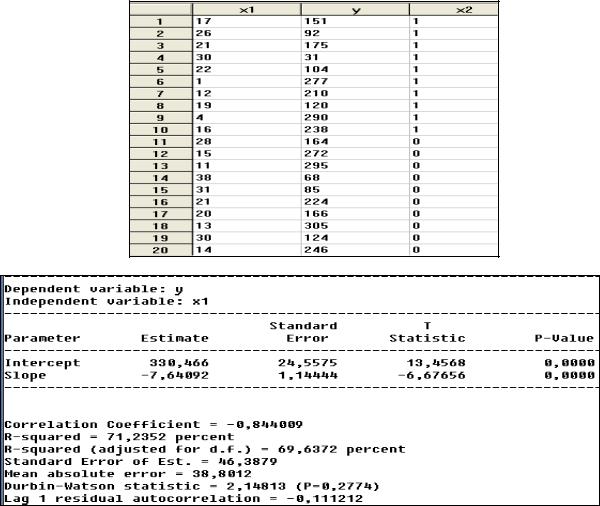
Провести полный корреляционно-регрессионный анализ информации отражающей расходы 34 стран на образование – у, валовой национальный продукт – х1 и численность населения – х2, протестировав остатки на гомоскедастичность и автокорреляцию и попытаться устранить в них нарушение предпосылок МНК о них, если таковые обнаружатся. Уравнение регрессии сначала рассчитать, анализируя расходы только в зависимости от ВНП, а затем подключить к расчетам и численность.
2.3.4. Регрессионные модели с переменной структурой (фиктивные переменные)
До сих пор мы рассматривали случаи, когда в модели регрессии в качестве объясняющих переменных выступали численные величины. Но иногда бывает полезно
вкачестве независимых переменных рассматривать символьные или, как их еще называют, категориальные переменные, которые позволяют различать качественные характеристики на основе количественных мер. Обычно в роли таких переменных выступают дихотомические или, по-другому, бинарные переменные, которые могут принимать только два значения (обычно это 0 или 1).
Например, необходимо количественно различить доходы служащих с высшим и без высшего образования, для мужчин и женщин, или объем реализации сельхозпродукции
взависимости от сезона и пр. Такие переменные обычно называются фиктивными. Они позволяют отслеживать структурные изменения в анализируемых явлениях или процессах. При этом необходимо иметь в виду, что количество таких переменных должно быть на единицу меньше, чем число уровней изучаемого признака. Например, в первых двух рассмотренных случаях фиктивных переменных должно быть по одной (они принимают значения 1, если речь идет о мужчине и 0, если о женщине, или 1, если работник с высшим образованием и 0 – без высшего). В случае с сезонной составляющей таких переменных должно быть три, если речь идет о квартальных данных и 11, если рассматриваются данные по месяцам. Это необходимо для того, чтобы матрица исходных данных не содержала линейно зависимых столбцов, тогда для
55
матрицы (ХтХ) можно будет рассчитать обратную матрицу, необходимую для вычисления оценок параметров уравнения регрессии.
Пример. Одна фиктивная переменная
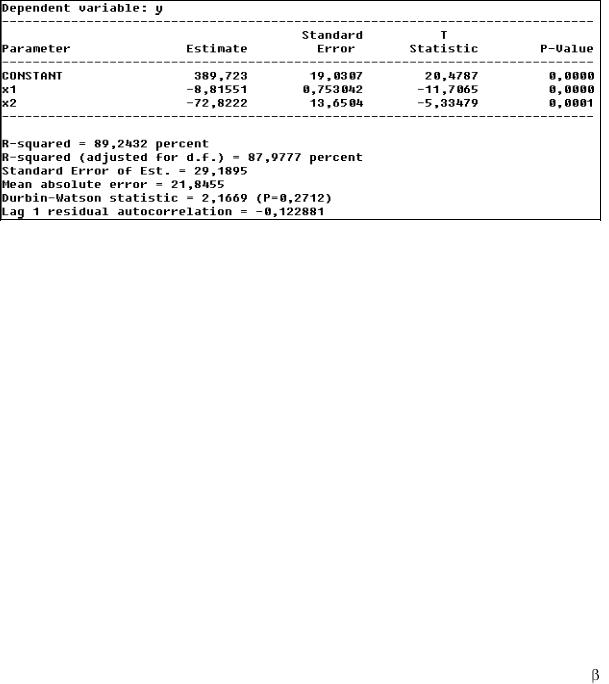
Рассмотрим пример применения фиктивной переменной для моделирования зависимости суммы страховых платежей (у) при размещении ценных бумаг в зависимости от времени размещения (х1) и вида ценной бумаги (х2). Причем, если речь идет об акциях, то х2 = 1, в противном случае х2 = 0. Исходная информация для примера следующая:
Рассчитаем уравнение регрессии для случая, когда ценные бумаги не различаются.
Рис. 46. Окно отчета об уравнении простой регрессии Здесь приведен сокращенный вариант отчета (без дисперсионного анализа
регрессии), поскольку для парной регрессии достаточно иметь показатель точности только, например, для коэффициента регрессии. Коэффициент Дарбина – Уотсона здесь рассчитан для значений, упорядоченных по возрастанию независимой переменной х1.
Итак, при анализе условий размещении ценных бумаг зависимость суммы страховых взносов (у) от времени их размещения (х1) описывается уравнением yˆ =
330,5 – 7,67х1 , если ценные бумаги не различаются по их видам. Если ценные бумаги разделить на облигации и прочие, то для облигаций такое уравнение будет иметь следующий вид: yˆ = 393 – 8,94* х1 (R2 = 91,4 %), а для прочих бумаг – yˆ = 314,4 –
8,67* х1 (R2 = 86,5 %). Последние два уравнения рассчитывались отдельно для акций и прочих ценных бумаг. Как видим, эти уравнения оказались более точными, чем в целом по всем ценным бумагам, что говорит о том, что информация о ценных бумагах более
56
однородная, если эти ценные бумаги разделить по их видам (число степеней свободы для каждого уравнения значительно уменьшилось, а уравнения оказались более точными). При этом, если коэффициенты при факторе “время” (при переменной х1) различаются незначимо, то свободные члены – существенно. При равном времени размещения сумма платежей для облигаций выше, чем для акций в среднем на величину 78,6 у.е. (надо сравнить свободные члены этих уравнений: 393 – 314,4 = 78,6).
Приведем уравнение множественной регрессии, где фиктивной переменной является переменная х2 (см рис. 47).
Рис. 47. Уравнение регрессии с фиктивной переменной Итак, уравнение регрессии имеет вид
yˆ = 389,7 – 8,81*х1 –72.8*х2, (R2 = 89,24%).
Как видим, оба коэффициента уравнения регрессии значимы и точность уравнения существенно выше, чем у парной регрессии. Свободный член этого уравнения указывает базу для сравнения прочих ценных бумаг с облигациями (платежи в среднем для прочих ценных бумаг ниже на 72,8 ден. ед.). Коэффициент Дарбина – Уотсона, равный 2,17, указывает на отсутствие ошибки в спецификации данного уравнения.
Пример. Несколько фиктивных переменных
Приведем далее в качестве примера использования фиктивных переменных результаты анализа рынка двухкомнатных квартир на основе уравнения множественной регрессии при следующем наборе переменных:
PRICE – цена;
TOTSP – общая площадь;
LIVSP – жилая площадь;
KITSP – площадь кухни;
DIST – расстояние до центра города;
WALK равна 1, если до станции метро можно дойти пешком, и равна 0, если надо воспользоваться общественным транспортом;
BRICK равна 1, если дом кирпичный и равна 0, если панельный;
FLOOR равна 1, если квартира не на первом и не на последнем этаже, и равна 0 в противном случае;
TEL равна 1, если в квартире есть телефон, и равна 0, если телефона нет; BAL равна 1, если есть балкон и равна 0, если нет.
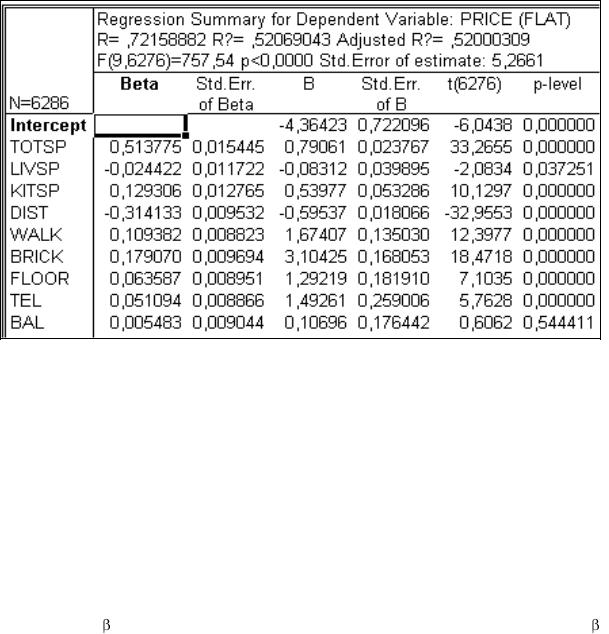
Расчеты проведены с помощью ППП STATISTICA (см. рис, 48). Наличие - коэффициентов позволяет упорядочить переменные по степени их влияния на зависимую переменную. Проведем краткий анализ результатов расчетов.
На основе статистики Фишера делаем вывод о значимости уравнения регрессии (р- величина < 0,05). В данном примере обработана информация о 6 286 квартирах (n–m–1 = 6 276, а m = 9). Все коэффициенты уравнения регрессии (кроме коэффициента при
57
переменной BAL) значимы (р-величины для них < 0,05). Наличие или отсутствие балкона в этом примере на цене квартиры существенно не сказывается.
Рис. 48. Отчет о рынке квартир на основе ППП STATISTICA
Коэффициент множественной детерминации равен 52 %, следовательно, включенные в регрессию переменные обусловливают изменение цены на 52 %, а остальные 48 % изменения цены квартиры зависят от неучтенных факторов. В том числе и от случайных колебаний цены.
Каждый из коэффициентов при переменной показывает, на сколько изменится цена квартиры (при прочих равных условиях), если данная переменная изменится на единицу. Так, например, при изменении общей площади на 1 кв. м цена квартиры в среднем изменится на 0,791 у. е. При удалении квартиры от центра города на 1 км цена квартиры в среднем уменьшится на 0, 596 у. е. и т. д. Фиктивные переменные (последние пять переменных в приведенном их перечне) показывают на сколько в среднем изменится цена квартиры, если перейти с одного уровня этой переменной на другой. Так, например, если дом кирпичный, то квартира в нем в среднем на 3,104 у. е. дороже, а наличие телефона в квартире поднимает ее цену в среднем на 1,493 у. е. и т. п.
На основе -коэффициентов можно сделать следующие выводы. Наибольшим - коэффициентом, равным 0,514 является коэффициент при переменной «общая площадь», следовательно в первую очередь цена квартиры формируется под влиянием ее общей площади. Следующий фактор по степени влияния на изменение цены квартиры является расстояние до центра города, затем материал, из которого сделан дом, затем площадь кухни и т. п.
58
Задания для самостоятельной работы Задание 1
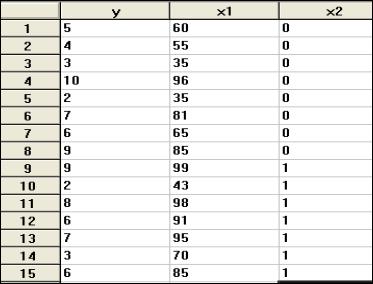
Имеется следующая информация: у – оценка производительности труда в баллах от 0 до 10 и х1 – тест на способность для 8 мужчин и 7 женщин, которые закодированы фиктивной переменной х2 (0 – мужчина, 1 – женщина).
Вычислить среднюю оценку производительности труда для мужчин и женщин и проверить, значимо ли они различаются. Подтвердить или опровергнуть полученные выводы, используя уравнение регрессии с фиктивной переменной, моделируя зависимость производительность труда в зависимости от теста на способность и пола работников фирмы.
Задание 2
Проанализировать с помощью фиктивных переменных, существенно ли различается зарплата работников фирмы (у) в зависимости от стажа работы (х1) и уровня образования, если фиктивные переменные х2 и х3 принимают значения: х2 = 1, если образование среднее специальное и 0 – в других случаях, х3 = 1, если образование среднее и 0 – в других случаях. Что является базой для сравнения зарплат в зависимости от образования в этом случае, если образование имеет три уровня – среднее, среднее специальное и высшее?
59
Глава 3. Анализ временных рядов
Рано или поздно экономист сталкивается с вопросами анализа социальноэкономических явлений во времени. Это достигается посредством построения и анализа статистических временных рядов. Временной ряд образуется из наблюдений, взятых через равные интервалы времени. Анализ временных рядов обычно преследует цель использования их для изучения явлений на основе сложившихся тенденций их развития в прошлом и использования этой информации для прогноза изучаемых процессов.
Методы анализа временных рядов представляет собой специальные статистические методы, поскольку временные ряды не являются статистически независимыми, а члены временного ряда не являются одинаково распределенными. Отдельные наблюдения над изучаемым процессом или явлением будем называть уровнем элемента временного ряда.
3.1. Характеристики временных рядов
Уровни элементов временного ряда обычно формируются под воздействием нескольких факторов, действующих в течение различных по протяженности промежутков времени.
Систематическую составляющую, действующую в течение длительного промежутка времени и формирующую основную тенденцию изменения уровней элементов временного ряда называют трендовой составляющей или трендом. Будем обозначать ее через Tt, где индекс t будет означать номер периода времени.
Регулярные колебания уровней элементов временного ряда, формирующиеся под воздействием систематически повторяющихся причин, называют сезонной составляющей. Будем обозначать ее через St.
Различают также циклическую составляющую, формирующуюся по воздействием долговременно действующих, но не регулярных факторов. Здесь мы их рассматривать не будем, отнеся к трендовой составляющей.

60
Удалив из уровней элементов временного ряда трендовую и циклическую компоненты, получим случайную составляющую, формирующуюся под воздействием случайных, кратковременно действующих факторов. Будем обозначать ее через It.
Относительно случайной составляющей будем предполагать, что она имеет те же свойства, что и отклонения в уравнении регрессии – нормальный закон распределения, нулевая средняя, гомоскедастичность. Это необходимо для определения показателей точности прогноза и указания интервальных оценок прогноза.
Если составляющие элементов временного ряда объединяются знаком произведения, то получаем мультипликативную модель временного ряда. Если составляющие элементов временного ряда объединяются знаком суммы, то получаем аддитивную модель временного ряда.
Математическая запись таких моделей следующая:
мультипликативная – Yt = Tt· St· It, аддитивная – Yt = Tt+ St+ It.
Процесс разложения элементов временного ряда на составляющие называется декомпозицией временного ряда.
Временные ряды подразделяются на стационарные и на не стационарные. Стационарным рядом называется ряд, основные статистические характеристики
которого не зависят от времени. Следовательно, стационарным будет тот ряд, уровни которого, меняясь с течением времени, не меняют своего среднего значения.
Если основные статистические характеристики ряда зависят от времени, то такой ряд является нестационарным. Если ряд имеет тренд, то он является не стационарным.
В зависимости от принадлежности временного ряда к тому или иному классу различаются методы их анализа и прогнозирования. Прежде чем перейти к их рассмотрению введем показатели точности прогноза.
3.2. Показатели точности прогноза
Любой прогноз несет на себе определенную степень ошибки, поэтому при проведении прогнозов исследователь всегда имеет дело со случайными отклонениями прогнозных значений от их реальных будущих значений. Такие отклонения, как было отмечено, предполагаются распределенными нормально, а мерой их рассеяния служат различные показатели точности прогноза.
Рассмотрим некоторые из них. Пусть yt – измеренные значения показателей временного ряда, а ft – прогнозные. Тогда ошибка прогноза за период времени t составит
et = yt – ft .
Средняя ошибка прогноза (МЕ) определяется из соотношения
ME 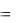 1/n et
1/n et
и характеризует степень смещенности прогноза. В идеальном случае МЕ 0. Если прогнозные значения в среднем завышены, то МЕ < 0, если занижены, то МЕ > 0.
Средний квадрат ошибки прогноза (MSE) определяется из соотношения
MSE 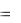 1/n et 2 .
1/n et 2 .
Средняя абсолютная ошибка (МАЕ) вычисляется из соотношения
MAE 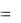 1/n et .
1/n et .
MSE и МАЕ используются для сравнения процедур прогноза и подбора параметров сглаживания.
Средняя абсолютная процентная ошибка (МРАЕ) вычисляется из соотношения:
МРАЕ 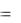 1/n
1/n 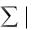 et / yt
et / yt 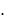 100
100
и используется для оценки качества прогноза.
61
Если МРАЕ < 10 %, то точность прогноза высокая, при 10 % < МРАЕ < 20 % – хорошая, если 20 % < МРАЕ < 50 %, то точность прогноза удовлетворительная и при МРАЕ > 50 % – неудовлетворительная. МРАЕ вычисляется по ошибке прогноза на шаг вперед.
Средняя процентная ошибка (МРЕ) вычисляется из соотношения
МРЕ 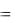 1/n (et / yt )
1/n (et / yt ) 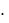 100
100
и служит показателем смещенности прогноза (не должна превышать 5 %).
Кроме того, в некоторых статистических ППП корень квадратный из MSE называется стандартной ошибкой и обозначается RMSE.
Из разработанных и используемых в практике методов анализа временных рядов рассмотрим лишь несколько наиболее простых, часто используемых на практике и теоретически обоснованных.
Как уже отмечалось, для стационарных и нестационарных временных рядов обычно применяются разные методы анализа. Поэтому в первую очередь ставится задача определения наличия или отсутствия тенденции в элементах временного ряда. Тенденцию можно определять визуально, построив горизонтальный график ряда. Но тенденция проявляется не всегда отчетливо. Поэтому для выявления тренда обычно используются статистические критерии, основанные на проверке статистических гипотез. Рассмотрим один из них, наиболее простой и часто используемый.
3.3. Анализ автокорреляций
Для определения существования зависимости может быть использован метод анализа автокорреляции.
Корреляция, как известно, измеряет степень тесноты линейной связи между двумя различными переменными. Автокорреляция измеряет степень такой же зависимости внутри самой переменной, т. е. “зависимость внутри переменной самой от себя”. Измеряется автокорреляция путем сопоставления фактического ряда данных с тем же рядом, но сдвинутым на некоторый промежуток времени с дальнейшим вычислением коэффициента корреляции между полученными рядами. Величина сдвига при этом называется лагом. Зависимость коэффициентов автокорреляции от величины лага называется автокорреляционной функцией, а график такой зависимости – коррелограммой.
Коэффициенты автокорреляции вычисляются по аналогии с линейным коэффициентом корреляции и поэтому характеризуют тесноту только линейной связи исходных и сдвинутых уровней ряда. По коэффициенту автокорреляции можно судить о наличии только линейной связи между уровнями ряда.
Для стационарных временных рядов закономерность в изменении значений коэффициентов автокорреляции для различных лагов отсутствует, а сами коэффициенты, как правило, незначимы (см. рис. 49 и 50).
Рис. 49. Пример горизонтального графика для стационарного ряда
62
Рис. 50. Коррелограмма для стационарного временного ряда Как видим (рис. 50), для стационарных временных рядов все коэффициенты
автокорреляции незначимы (не выходят за пределы доверительной области нуля).
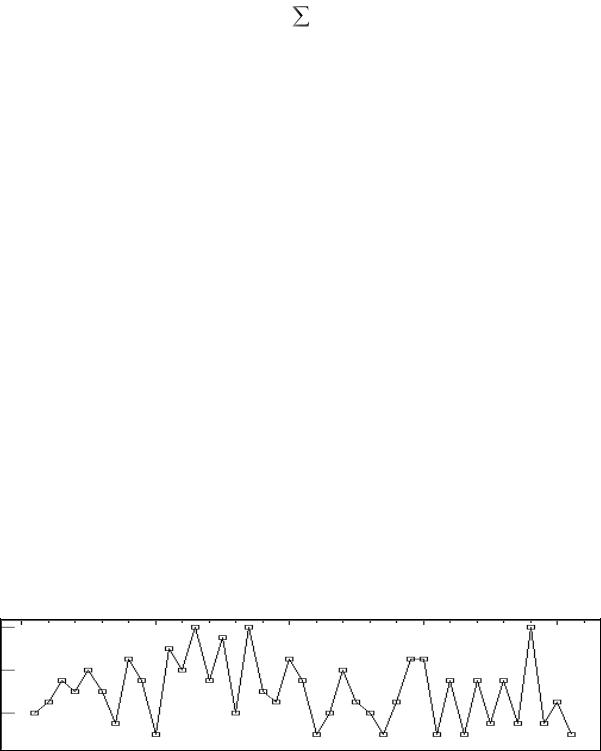
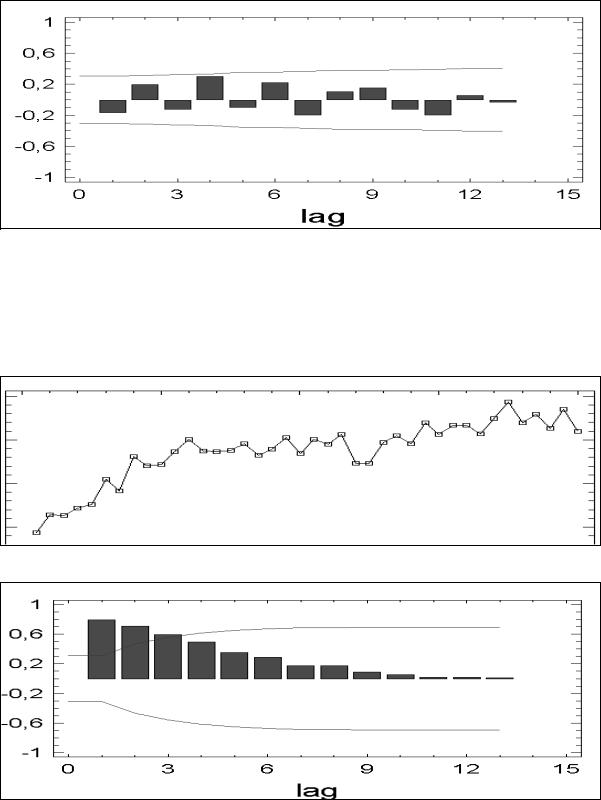
При наличии тренда коэффициенты автокорреляции в среднем уменьшаются с увеличением лага, а максимальное значение соответствует лагу, равному единице (см. рис. 51 и 52). При этом несколько первых коэффициентов значимо отличаются от нуля (выходят за пределы доверительной области нуля).
Рис. 51. Пример горизонтального графика для временного ряда с трендом
Рис. 52. Коррелограмма для временного ряда с трендом Известно, что анализ автокорреляции первых разностей для ряда с линейным
трендом обычно показывает их стационарность.
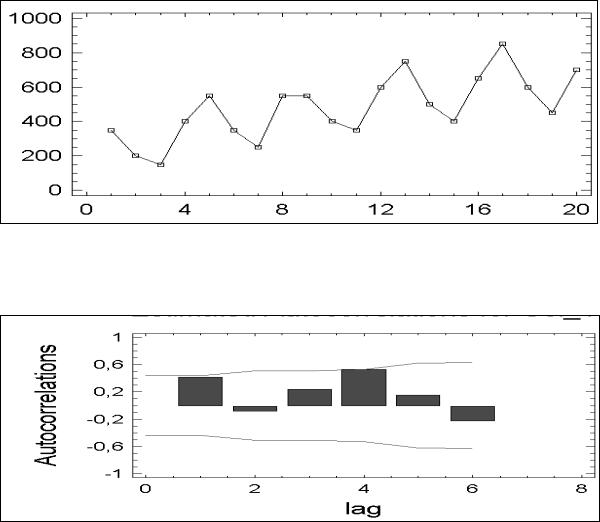
При сезонной составляющей максимальное значение коэффициента автокорреляции наблюдается при лаге, кратном величине сезонности (4 – при квартальных данных и 12 – при помесячных).
63
Например, для следующего временного ряда (рис. 53) явно прослеживается сезонная составляющая с длиной сезонности, равной 4.
Рис. 53. Пример горизонтального графика временного ряда с сезонной составляющей и трендом
Это и отражено в коррелограмме (рис. 54). Здесь наибольший коэффициент автокорреляции наблюдается при лаге, равном 4. Наличие тренда отражено значительным коэффициентом автокорреляции первого порядка.
Рис. 54. Коррелограмма для временного ряда с сезонной составляющей и трендом При комбинации разных видов зависимостей между уровнями элементов
временного ряда наблюдается более сложная картина изменения коэффициентов автокорреляции. Для более сложных зависимостей необходимы и более сложные методы их анализа, например, ARIMA – модели, которые здесь не рассматриваются.
3.4. Модели стационарных временных рядов
Методы прогнозирования стационарных временных рядов весьма разнообразны. Рассмотрим сначала наиболее простые из них, а именно: вычисление скользящих средних и экспоненциально взвешенных скользящих средних.
Если в первом случае для усреднения используются простые средние арифметические, вычисление которых как бы скользит по элементам исследуемого временного ряда, то во втором случае вычисляются взвешенные средние, причем веса подобраны так, что менее удаленным по времени наблюдениям приписываются большие веса, а более удаленным – меньшие. Здесь как бы учитывается процесс старения информации и более ценной является более свежая информация. В случае вычисления экспоненциально взвешенных скользящих средних веса убывают по экспоненте по мере удаления элементов временного ряда от рассматриваемого периода. Отсюда и название метода.

64
|
Проиллюстрируем |
идею |
этого метода на примере расчета простого |
экспоненциально взвешенного среднего (Брауна). |
|||
|
Пусть прогнозное значение на период t рассчитывается по формуле |
||
|
ft = yt + |
(1– |
)yt-1 + (1– )2 yt-2 +…+ (1– )n yt- n + … , |
где |
– показатель, |
характеризующий вес текущего наблюдения, называемый |
|
параметром сглаживания.
Теоретически здесь предполагается бесконечный временной ряд, но в силу того, что 0 < 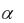 < 1, коэффициенты-веса при соответствующих элементах временного ряда быстро убывают, поэтому достаточно несколько первых слагаемых этой суммы, чтобы получить результат с достаточной точностью.
< 1, коэффициенты-веса при соответствующих элементах временного ряда быстро убывают, поэтому достаточно несколько первых слагаемых этой суммы, чтобы получить результат с достаточной точностью.
Преобразуем это выражение. Вынесем за скобку (1– |
). |
|||
ft = yt + (1– |
)[ |
yt-1 + |
(1– )yt-2 +…+ |
(1– )n-1 yt-n + …]. |
Тогда можем записать: |
|
|
|
|
ft = |
yt |
+ (1– |
)ft-1. |
(3.1) |
Тем самым мы получили модель экспоненциально взвешенной средней. Из (3.1) следует, что для того чтобы вычислить экспоненциально взвешенную среднюю, необходимо знать значение элемента временного ряда в текущем периоде и экспоненциально взвешенную среднюю за предыдущий период.
Отметим, что сумма весов в выражении для экспоненциально взвешенной скользящей средней (как сумма бесконечно убывающей геометрической прогрессии) равна единице.
Параметр сглаживания обычно подбирается по минимальной ошибке прогноза. С этой целью перебираются возможные значения (с некоторым шагом) и для каждого из них рассчитываются экспоненциально взвешенные скользящие средние и вычисляется ошибка прогноза, например, MSE. Минимальная ошибка и определит
константу сглаживания. При расчетах на ЭВМ особых проблем при подборе |
не |
возникает ввиду автоматизации таких расчетов. |
|
Есть разные рекомендации по выбору возможных значений , основная из которых заключается в том, что при анализе стационарных временных радов параметр сглаживания не должен выходить за пределы интервала 0,05 – 0,3. Считается, что если при вычислении экспоненциально взвешенных скользящих средних при увеличении
значения |
(за пределами |
> 0,3) ошибка прогноза уменьшается, то речь идет о не |
||
стационарных временных рядах. |
|
|
||
Следует отметить, что при увеличении |
прогнозные значения более динамичны и |
|||
в большей мере отражают |
динамику исходных данных, и, наоборот, чем меньше |
, |
||
тем прогнозные значения |
более сглажены. Поэтому, когда по ходу решения задачи |
|||
требуется |
повысить чувствительность прогноза к динамике исходных данных, |
то |
||
высокие значения могут быть оправданы.
При расчетах по модели (3.1) встает проблема определения прогнозного значения на начальный период (при t = 1, т.е. f0). Обычно за f0 берут либо y1, либо среднее значение нескольких первых членов ряда. Как правило, на конечный результат расчетов выбор начального значения f0 практически не сказывается.
3.5. Модели нестационарных временных рядов
3.5.1. Прогноз по тренду
Нестационарные условия – это когда среднее значение процесса не остается постоянным с течением времени. Изменяющееся среднее принято называть трендом.
Таким образом, тренд – это основная тенденция развития процесса или явления во времени. Линия тренда может быть описана аналитическим выражением, полученным, например, на основе МНК в виде уравнения регрессии по времени, либо получена на основе вычисления скользящих средних.
65
Вид тренда зависит от характера изменения изучаемого процесса. Например, линейный тренд характеризует процесс изменения с постоянным темпом роста b и записывается в виде
Тt = a + bt,
а экспоненциальный тренд – с постоянным темпом прироста b:
Тt = a ebt.
При вычислениях с помощью ППП предусматривается возможность подбора оптимального вида тренда (среди многих возможных), минимизирующего, например, MSE или MAE.
В ППП Statgraphics, например, в процедуре прогнозирования временных рядов предусмотрено четыре вида тренда: линейный, квадратичный, экспоненциальный и по S – кривой, а при подборе вида модели в простой регрессии – 12 видов трендов.
Прогноз на основе тренда (вернее точечная оценка прогноза) осуществляется путем подстановки в уравнение тренда численного значения для переменной t с дальнейшим расчетом интервальной оценки.
Следует иметь в виду, что прогноз на основе тренда осуществляется по принципу: «что будет, если условия функционирования изучаемого явления не изменятся?».
3.5.2. Прогнозирование на основе сезонной компоненты (сезонная декомпозиция временного ряда)
Усложним постановку задачи. Будем считать, что на формирование значений показателей временного ряда оказывают влияние все три вышерассмотренных фактора: случайная компонента, трендовая компонента и сезонная компонента. От случайной компоненты обычно избавляются путем усреднения, например, простыми скользящими или экспоненциально взвешенными средними, трендовую компоненту можно выделить, например, используя МНК, как в предыдущем пункте.
Для прогнозирования временного ряда, включающего все три компоненты, необходимо определить, каким образом они сочетаются при формировании значений элементов ряда. Как известно, различают два способа такого сочетания: мультипликативный, когда значения элементов временного ряда формируются под воздействием произведения его компонент:
Yt = Tt St It,
и аддитивный:
Yt = Tt + St + It,
если компоненты складываются.
Если вклад сезонной компоненты остается на постоянном уровне для всего рассматриваемого периода времени, то рекомендуется использовать аддитивное представление, а если с течением времени вклад сезонной компоненты изменяется, то рекомендуется использовать мультипликативное представление элементов временного ряда.
Вмоделях с аддитивным и с мультипликативным представлением компонент элементов временного ряда процедура анализа в принципе одинакова. Обычно она состоит в установлении и выделении воздействия на величину элементов временного ряда каждой компоненты по отдельности. Этот процесс называется сезонной декомпозицией временного ряда.
3.5.3. Прогноз по экспоненциально взвешенным скользящим средним (адаптивные методы прогнозирования)
Вэтом направлении разработан целый комплекс моделей. Кратко рассмотрим некоторые из них.
Линейное экспоненциальное сглаживание Холта предполагает, что среднее прогнозируемого показателя yt изменяется во времени линейно:

66
yt = μ + λt + εt,
где μ – среднее процесса, λ – его скорость, а εt – случайная ошибка. При этом оценка λ осуществляется по показателю роста bt, который вычисляется как экспоненциально взвешенное среднее разности между текущими экспоненциально взвешенными средними значениями элементов временного ряда ut и их предыдущими значениями ut-1 и предыдущим значением bt-1. В свою очередь, текущее значение экспоненциально взвешенного среднего ut включает в себя значение прошлого показателя роста bt-1, адаптируясь таким образом к предыдущему значению линейного тренда.
Уравнения метода Холта:
ut = αyt +(1–α)(ut-1 + bt-1) и bt = β(ut–ut-1) + (1–β)bt-1,
где α и β – параметры сглаживания.
Если τ – горизонт прогнозирования, то прогноз на τ моментов времени по модели Холта вычисляется по формуле
ft+τ = ut + bt τ.
Здесь ut – оценка среднего текущего значения, bt – ожидаемый показатель изменения.
Значения α и β подбираются по минимальной ошибке прогноза. Параметр α предназначен для сглаживания оценки постоянного уровня элементов временного ряда, β – для оценки тренда.
Линейное экспоненциальное сглаживание Брауна предполагает, что прогноз на τ
моментов времени вычисляется по формуле |
|
|
|
ft+τ = ut + bt τ, |
|
где ut = ut-1+ bt-1+ (1– γ)2et, et = yt– ft |
и |
bt = bt-1+ (1– γ)2et. |
Квадратичное экспоненциальное сглаживание Брауна предполагает, что прогноз на
τ моментов времени вычисляется по формуле
ft+τ = а0 + а1 τ + а2 τ2,
причем параметры а0, а1 и а2 выбираются так, чтобы на любой момент времени i взвешенная сумма квадратов отклонений между наблюдаемыми и ожидаемыми значениями обращалась в минимум:
i ( yt i 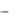 ft i )2 = min.
ft i )2 = min.
Параметр γ в методе Брауна аналогичен параметру (1–α) в методе Холта (показатель дисконтирования наблюдений) и задается из априорных соображений, в том числе и из условия минимизации указанной суммы.
Кроме рассмотренной модели кратко остановимся на модели Винтера с сезонной компонентой. Эта модель, как и модели Холта и Брауна, основывается на экспоненциально взвешенных средних. Оценке здесь подлежат отдельно каждая из составляющих ряда: стационарная, трендовая (в виде линейного тренда) и сезонная. Для каждой такой оценки вводятся свои параметры сглаживания: α, β и γ. При компьютерных расчетах они определяются в автоматическом режиме по минимальной ошибке прогноза. При этом прогноз на τ периодов времени строится из трех элементов: суммируется оценка линейного тренда bt и оценка стационарного фактора ut, и результат умножается на значение коэффициента сезонности St+τ:
ft+τ = (ut + btτ) St-s+τ.
При этом оценки ut и bt расчитываются аналогично, как в модели Холта (с учетом сезонности), а для оценки сезонной составляющей используется третий параметр (γ) и вычисления ведутся по формуле
St = γ(yt/ut) + (1–γ)St-s+ τ.
Здесь s – длина сезонности.
