
1
Определителем n-го порядка квадратной матрицы называется число, равное алгебраической сумме n! слагаемым, каждое из которым представляет собой произведение и элементов, взятых по одному из каждой строки и каждого столбца определителя. Произведения отличаются одно от другого набором элементов. Перед каждым произведением ставится знак "+" или "—'\
О![]() пределим
знак перед произведением. Поскольку в
каждом произведении присутствует один
элемент из 1-й строки, один элемент из
2-ой и т.д.. то произведение можно записать
так:
пределим
знак перед произведением. Поскольку в
каждом произведении присутствует один
элемент из 1-й строки, один элемент из
2-ой и т.д.. то произведение можно записать
так:
Здесь i.j. к.....s - номера столбцов, в которых стоят элементы, выбранные из
1-й. 2-й. 3-й, ... л-й строк, соответственно. Из сказанного выше ясно, что каждое из различных чисел ij, к, .... s равно какому-либо из чисел 1. 2. .... п.
Расположенные в данном порядке номера столбцов ij, к. .... s, образуют перестановку из чисел 1, 2, .... п. Всего существует п\ различных перестановок из п натуральных чисел.
Инверсией называется взаимное расположение двух чисел в перестановке, когда большее предшествует меньшему. Например, в перестановке 4.1.3,6.5 три инверсии, а в перестановке 3.7.4.2.5.6 - шесть инверсий.
Перестановка называется четной, если в ней четное число инверсий и нечетной, если число инверсий нечетное.
Tогда
произведение
![]() берется
со знаком
"+".
если индексы столбцов образуют четную
перестановку, и со знаком "—", если
- нечетную.
берется
со знаком
"+".
если индексы столбцов образуют четную
перестановку, и со знаком "—", если
- нечетную.
Определитель квадратной матрицы равен сумме произведений элементов некоторой строки или столбца на их алгебраические дополнения.
2
Свойства определителей
-
Определитель не изменяется при транспонировании: detAT=detA.
-
Если строка (столбец) матрицы A равна линейной комбинации соответственных строк (столбцов) матриц A и B, а остальные строки (столбцы этих матриц совпадают), то ее определитель равен линейной комбинации определителей матриц A и B:
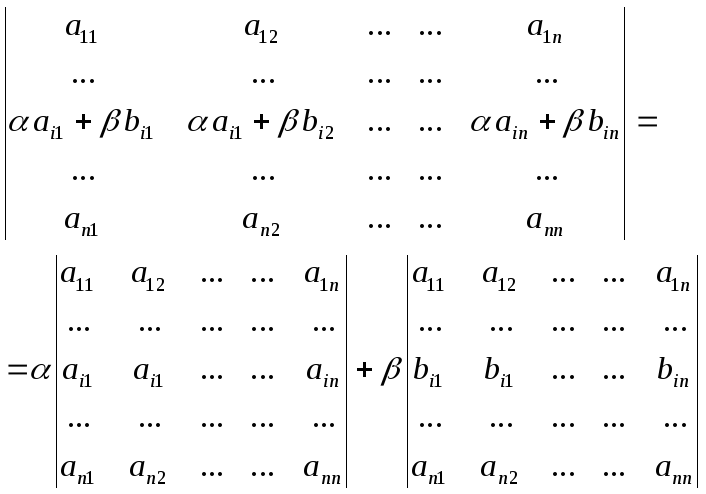
-
При перестановке любых двух строк (столбцов), определитель меняет знак.
-
Если в определителе есть две одинаковые строки (два одинаковых столбца), то он равен нулю.
-
Если в определителе есть две пропорциональные строки (два пропорциональные столбца), то он равен нулю.
-
Определитель не изменится, если к элементам любой его строки (столбца) прибавить элементы любой другой строки (столбца), умноженные на одно и то же число.
-
Определитель, содержащий нулевую строку (нулевой столбец), равен нулю.
-
Сумма произведений элементов любой строки (столбца) на алгебраические дополнения другой строки (другого столбца) равна нулю.
-
Определитель произведения двух квадратных матриц равен произведению определителей сомножителей.
3
ФОРМУЛЫ КРАМЕРА
Матричное
равенство
![]() запишем в виде:
запишем в виде:
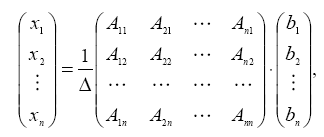
тогда имеем
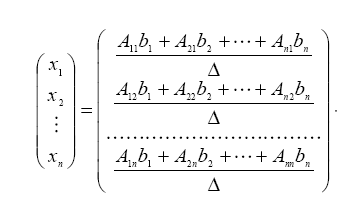
Или

Здесь
![]() есть разложение определителя
есть разложение определителя
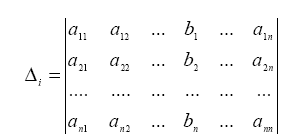
по элементам i-го столбца.
Тогда имеем

Полученные формулы называются формулами Крамера.
Таким образом, невырожденная система л линейных уравнений с п неизвестными имеет единственное решение, которое может быть найдено также по формулам Крамера.
6
Под скалярным произведением двух векторов а и b понимается число, равное произведению длин этих векторов на косинус угла между ними. т. е. в обычных обозначениях:
![]()
Заметим,
что в приведенной формуле скалярное
произь еще записывать как
![]() опуская
точку. Так как
опуская
точку. Так как
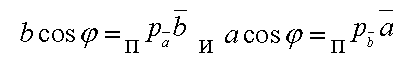
то можно записать
![]()
т. е. скалярное произведение двух векторов равно длине одного из них, умноженной на проекцию другого на ось с направлением первого.



7
Определение 1.
Векторным
произведением
двух векторов
![]() и
и
![]() называют третий вектор
называют третий вектор
![]() ,
удовлетворяющий следующим требованиям:
,
удовлетворяющий следующим требованиям:
1) вектор
![]() перпендикулярен векторам
перпендикулярен векторам
![]() и
и
![]() ;
;
2) тройка векторов
![]() ,
,![]() ,
,![]() правая;
правая;
3) модуль векторного
произведения равен площади параллелограмма,
построенного на перемножаемых векторах,
т.е.
![]()
Обозначают векторное
произведение так
![]()
Рассмотрим
ортонормированный базис
![]() .
.
Согласно определению векторного произведения найдем:
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
(5)
.
(5)
Отметим следующие свойства векторного произведения.
-
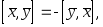
-

-
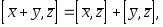 4)
4)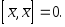
Определение 2.
Смешанным
произведением трех
векторов
![]() ,
,![]() ,
,![]() называют число, равное
называют число, равное
![]()

![]() ,
,![]() ,
,![]() выберем в качестве ребер и построим
параллелепипед. Пусть
выберем в качестве ребер и построим
параллелепипед. Пусть
![]() тогда
тогда
![]() -площадь
основания паралле-лепипеда, а смешанное
произведение
-площадь
основания паралле-лепипеда, а смешанное
произведение
![]()
Здесь H - высота параллелепипеда, а V – его объем.
Таким образом,
смешанное произведение только знаком
может отличаться от объема параллелепипеда,
построенного на перемножаемых векторах
как на ребрах. Если тройка
![]() правая, то знак смешанного произведения
будет положительным.
правая, то знак смешанного произведения
будет положительным.
Из геометрического
смысла смешанного произведения ясно,
что векторно можно перемножать любые
два из трех векторов, от этого может
измениться только знак. Легко проверить,
что тройки векторов
![]() ,
,
![]() и
и
![]() одинаковой ориентации, так что
одинаковой ориентации, так что
![]() = =
= =![]() =
=
![]() Поэтому смешанное произведение обозначают
Поэтому смешанное произведение обозначают
![]() не
указывая, какие векторы перемножаются
векторно.
не
указывая, какие векторы перемножаются
векторно.
Теорема. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.
Доказательство ясно из геометрической интерпретации смешанного произведения.
Следствие.
Три вектора
![]() линейно независимы только в том случае,
если их смешанное произведение отлично
от нуля.
линейно независимы только в том случае,
если их смешанное произведение отлично
от нуля.
Доказательство очевидно.
Обобщим понятие вектора. Назовем вектором упорядоченную совокупность n действительных чисел, т.е.
![]() вектор,
вектор,
![]() его
координаты.
его
координаты.
При сложении векторов их соответствующие координаты будем складывать, а при умножении на число- умножать на это число.
Множество всех
таких векторов с определенными выше
операциями называют арифметическим
пространством
и обозначают
![]() Обычное пространство геометрических
векторов обозначают
Обычное пространство геометрических
векторов обозначают
![]() множество компланарных геометрических
векторов -
множество компланарных геометрических
векторов -
![]() коллинеарных
-
коллинеарных
-
![]()
Зафиксировав в
пространстве
![]() ортонормированный базис
ортонормированный базис
![]() ,
понятия скалярного, векторного и
смешанного произведений можно обобщить
и на векторы этого пространства
,
понятия скалярного, векторного и
смешанного произведений можно обобщить
и на векторы этого пространства
![]()
8

9
Отметим следующие свойства векторного произведения.
-

-
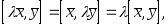
-
 4)
4)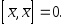
10

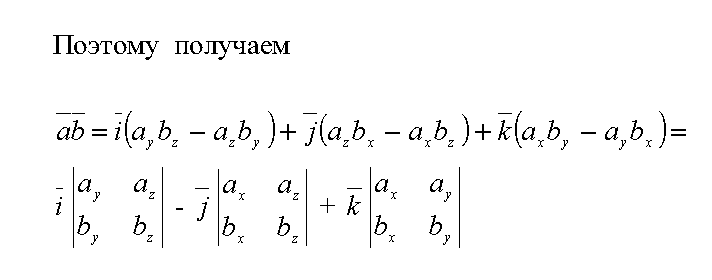
11
Из геометрического
смысла смешанного произведения ясно,
что векторно можно перемножать любые
два из трех векторов, от этого может
измениться только знак. Легко проверить,
что тройки векторов
![]() ,
,
![]() и
и
![]() одинаковой ориентации, так что
одинаковой ориентации, так что
![]() = =
= =![]() =
=
![]() Поэтому смешанное произведение обозначают
Поэтому смешанное произведение обозначают
![]() не
указывая, какие векторы перемножаются
векторно.
не
указывая, какие векторы перемножаются
векторно.
Выразим смешанное произведение через координаты перемножаемых векторов в ортонормированной системе координат.
Пусть
![]()
Поскольку![]() ,
то
,
то
![]() =
=
=
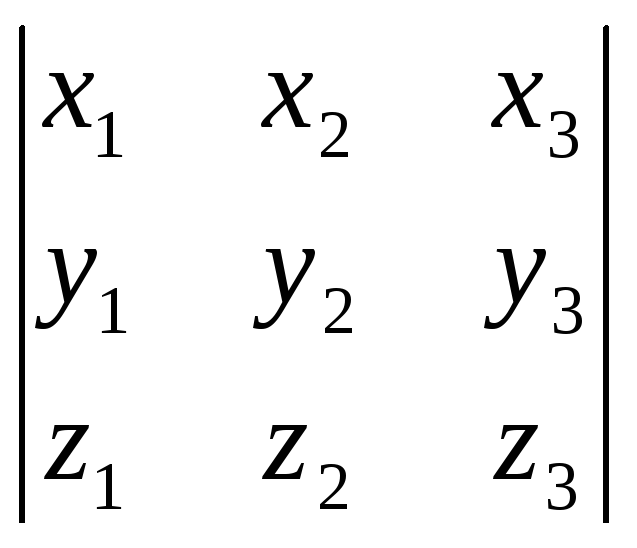 .
.
12




13





15



19
Необходимое и достаточное условие совместности системы линейных алгебраических уравнений
На вопрос о совместности системы линейных алгебраических уравнений отвечает следующая теорема.
Теорема (теорема Кронекера-Капелли). Для того, чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы.
Доказательство. Заметим, что расширенная матрица системы получается из матрицы системы добавлением столбца правых частей.
Необходимость.
Запишем систему в виде
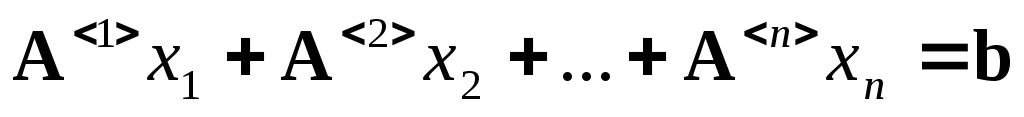 .
Если система совместна, то существуют
такие
.
Если система совместна, то существуют
такие
![]() ,
при которых
,
при которых
 ,
т.е. столбец правых частей линейно
выражается через столбцы матрицы системы
и, следовательно, добавление его к
матрице не увеличивает числа линейно
независимых столбцов и, значит, ранг
расширенной матрицы системы равен рангу
матрицы системы. Что и требовалось
доказать.
,
т.е. столбец правых частей линейно
выражается через столбцы матрицы системы
и, следовательно, добавление его к
матрице не увеличивает числа линейно
независимых столбцов и, значит, ранг
расширенной матрицы системы равен рангу
матрицы системы. Что и требовалось
доказать.
Достаточность.
Если ранг матрицы системы совпадает с
рангом расширенной матрицы системы, то
у них совпадают базисные столбцы. Пусть
RgA
= RgAp
= r
и базисными являются первые r
столбцов матрицы A:
![]() .
Тогда столбец правых частей линейно
выражается через базисные столбцы:
.
Тогда столбец правых частей линейно
выражается через базисные столбцы:
![]() .
.
Положим
![]() ,
тогда
,
тогда
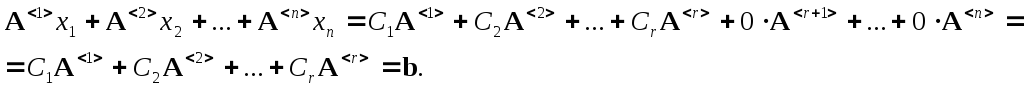
Таким
образом
![]() — решение рассматриваемой неоднородной
системы, и, следовательно, система
совместна.
— решение рассматриваемой неоднородной
системы, и, следовательно, система
совместна.
Теорема доказана.
Замечания
-
Однородная система всегда совместна. Действительно, добавление нулевого столбца не увеличивает количество линейно независимых столбцов матрицы.
-
Для того, чтобы система n линейных алгебраических уравнений относительно n неизвестных имела единственное решение, необходимо и достаточно, чтобы ранг матрицы системы был равен числу неизвестных. Докажем достаточность. Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных (m=n) у которой пусть ранг матрицы системы равен числу неизвестных: (RgA = n), т.е. detA0 и, следовательно, матрица системы A обратима.
Умножим слева обе
части матричного
уравнения
![]() на
матрицу
на
матрицу
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
т.е. система имеет
единственное решение, которое можно
вычислить по формуле
![]() .
.
В приведенном выше доказательстве система линейных алгебраических уравнений решена как матричное уравнение.
20
Если заранее
оговорить условие, что прямая лежит в
плоскости z = 0, то второе уравнение в (7)
можно опустить. В результате получим
уравнение
![]() .
(8)
.
(8)
Уравнение (8)
называют общим уравнением прямой на
плоскости xOy.
Если
![]() то
из (8) получим
то
из (8) получим
![]() .
(9)
.
(9)
![]() ,
где
,
где
![]() -
угол между прямой и осью Ox.
-
угол между прямой и осью Ox.
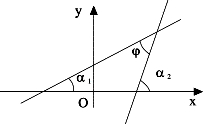
Найдем
угол между двумя прямыми
![]() ,
,
![]() .
.
Поскольку
![]() то
то
![]() ,
,
![]() . (10)
. (10)
Из равенства (10) можно получить условие параллельности и перпендикулярности двух прямых на плоскости:
![]() . (11)
. (11)
Нормальное уравнение
прямой и уравнение в отрезках на плоскости
получаются из соответствующих уравнений
плоскости при z = 0. Отклонение точки
![]() от прямой также получается из
соответствующей формулы для плоскости
при z = 0.
от прямой также получается из
соответствующей формулы для плоскости
при z = 0.
22

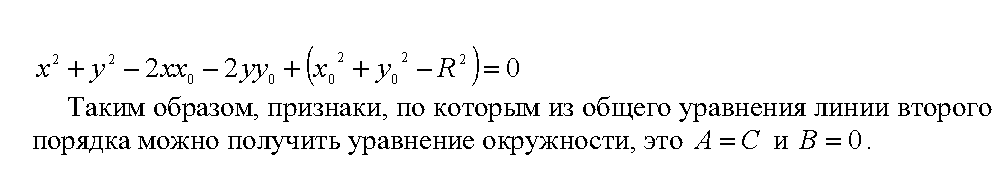


23


24

35
Определение линейного пространства
Пусть
M
—множество элементов произвольной
природы, для которых определены операции
сложения и умножения на действительное
число, т.е. каждой паре элементов множества
![]() отвечает
элемент
отвечает
элемент
![]() ,
называемый суммой x
и y,
и каждой паре
,
называемый суммой x
и y,
и каждой паре
![]() ,
,
![]() —
любое действительное число, отвечает
элемент
—
любое действительное число, отвечает
элемент
![]() ,
называемый произведением числа
,
называемый произведением числа
![]() и элемента
x.
и элемента
x.
Будем
называть множество M
линейным
пространством, если
для всех его элементов определены
операции сложения и умножения на
действительное число и для любых
элементов
![]() и
произвольных чисел
и
произвольных чисел
![]() справедливо:
справедливо:
-
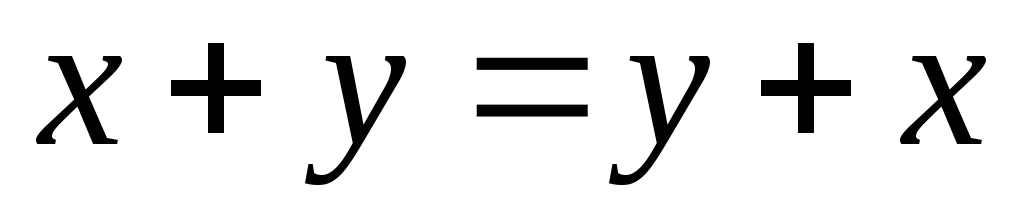 ,
сложение коммутативно;
,
сложение коммутативно; -
 ,сложение
ассоциативно;
,сложение
ассоциативно; -
существует единственный нулевой элемент
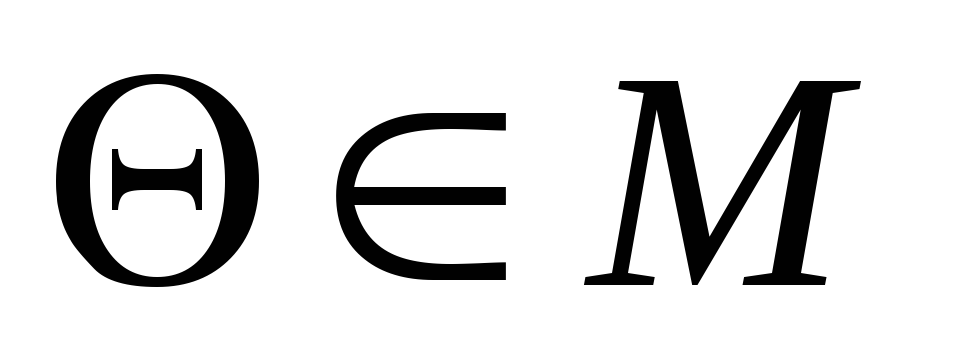 такой,
что
такой,
что
 ;
; -
для каждого элемента существует единственный противоположный элемент -x такой, что
 ,
, -
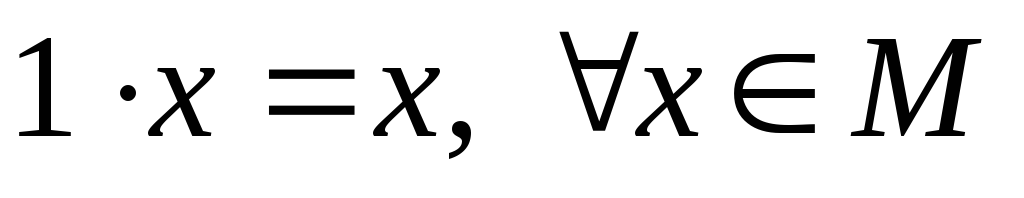 ;
; -
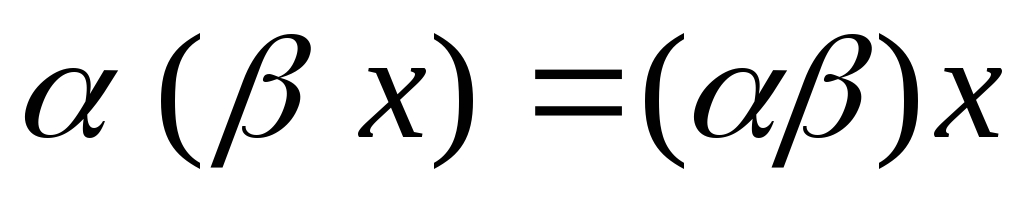 ,
,
 ,
,
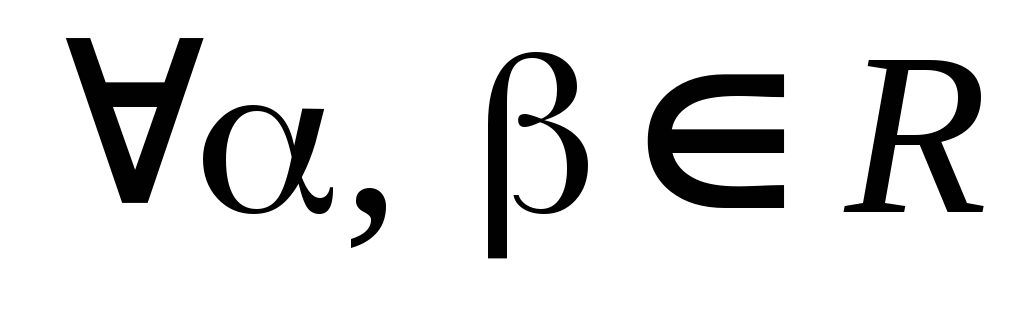 ,
умножение на число ассоциативно;
,
умножение на число ассоциативно;
-
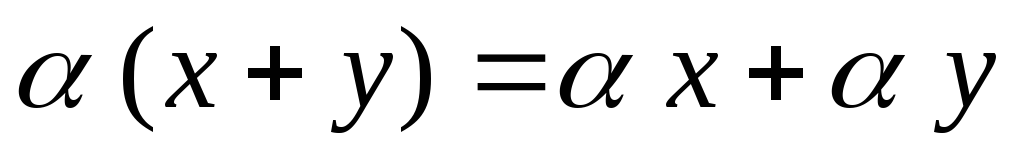 ,
,
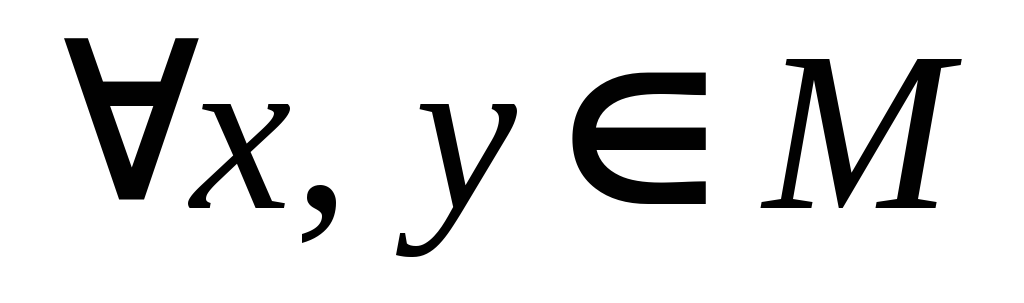 ,
,
 ,умножение
на число дистрибутивно относительно
сложения элементов;
,умножение
на число дистрибутивно относительно
сложения элементов; -
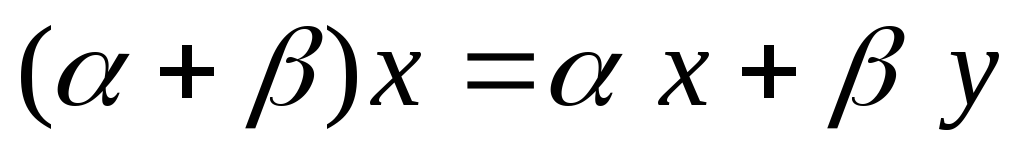 ,
умножение вектора на число дистрибутивно
относительно сложения чисел.
,
умножение вектора на число дистрибутивно
относительно сложения чисел.
Равенства 1—8 называют аксиомами линейного пространства.
Линейное пространство часто называют векторным пространством, а его элементы — векторами. Такое название, как будет показано ниже, вполне содержательно.
Определение.
Линейной
комбинацией
элементов
![]() линейного пространства L
называется
выражение вида
линейного пространства L
называется
выражение вида
![]() ,
где
,
где
![]() — произвольные действительные числа.
— произвольные действительные числа.
Определение.
Говорят, что вектор
![]() линейного пространства L
линейно выражается через
векторы
линейного пространства L
линейно выражается через
векторы
![]() ,
если его можно представить в виде
линейной
комбинации
этих элементов, т.е. представить в виде
,
если его можно представить в виде
линейной
комбинации
этих элементов, т.е. представить в виде
![]() .
.
Определение.
Система
![]() векторов произвольного линейного
пространства называется линейно
независимой,
если из равенства
векторов произвольного линейного
пространства называется линейно
независимой,
если из равенства
![]() следует равенство нулю всех коэффициентов
следует равенство нулю всех коэффициентов
![]() .
.
Определение. Система векторов, которая не является линейно независимой, называется линейно зависимой.
Необходимое и достаточное условие линейной зависимости системы векторов
Справедливо следующее утверждение.
Теорема.
Система
![]() векторов произвольного линейного
пространства линейно зависима тогда и
только тогда, когда хотя бы один из
векторов системы линейно выражается
через остальные.
векторов произвольного линейного
пространства линейно зависима тогда и
только тогда, когда хотя бы один из
векторов системы линейно выражается
через остальные.
Это утверждение (необходимое и достаточное условие линейной зависимости) доказано на лекции.
Некоторые свойства линейно зависимых и линейно независимых систем векторов линейного пространства
Утверждение 1. Любая система векторов линейного пространства, содержащая нулевой вектор, — линейно зависима.
Утверждение 2. Любая система векторов линейного пространства, содержащая два равных вектора, — линейно зависима.
Утверждение 3. Любая система векторов линейного пространства, содержащая два взаимно противоположных вектора, — линейно зависима.
Утверждение 4. Любая подсистема линейно независимой системы векторов — линейно независима.
Размерность линейного пространства. Базис линейного пространства
Определение. Пусть L — линейное пространство. Если существует такое натуральное число n, что
-
в пространстве L существует система из n линейно независимых векторов;
-
любая система из n + 1 вектора линейно зависима,
то число
n называется размерностью линейного пространства. L. Ообозначаем dimL=n.
Пример. Размерность пространства геометрических радиусов-векторов R3 равна 3, dim R3=3.
Действительно, существует система из 3-х линейно независмых векторов (i, j, k), а любые четыре вектора — линейно зависимы.
Определение.
Упорядоченная
совокупность векторов
![]() линейного пространства L называется
базисом этого пространства, если
линейного пространства L называется
базисом этого пространства, если
-
они линейно независимы;
-
любой вектор из L линейно выражается через векторы
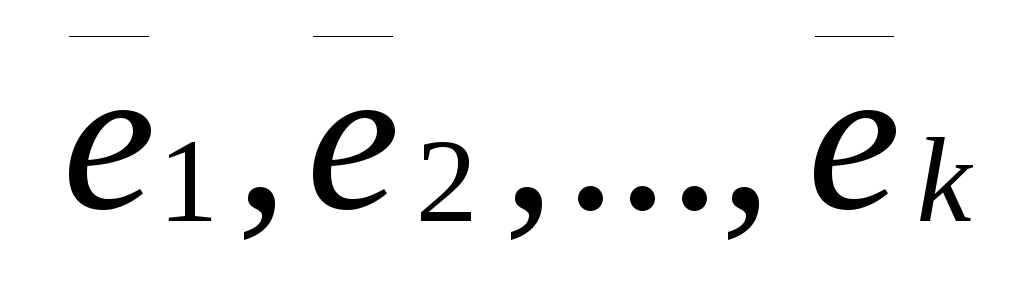 ,
т.е. для любого x
из L
существуют такие числа
,
т.е. для любого x
из L
существуют такие числа
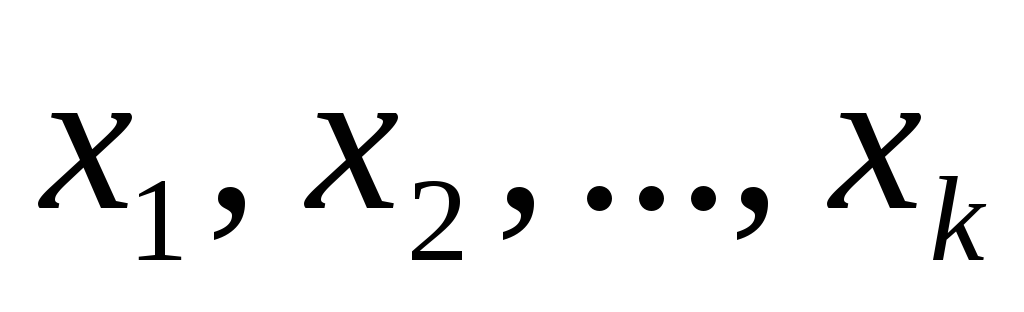 что
что
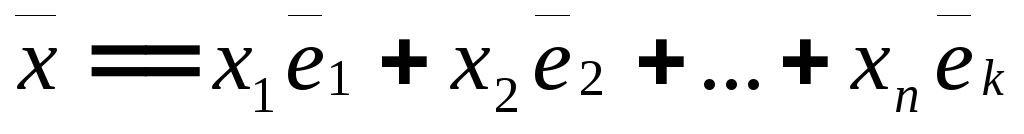 .
.
Справедливы следующие утверждения:
Теорема (о единственности разложения по базису). Любой вектор линейного пространства линейно выражается через векторы базиса единственным способом.
Теорема (о базисе n-мерного пространства). В n-мерном линейном пространстве существует базис из n векторов.
Теорема.
Любая упорядоченная линейно независимая
система n
векторов n-мерного
линейного
пространства
![]() образует
базис этого пространства.
образует
базис этого пространства.
Эти утверждения на лекции доказаны.
Выражение
![]() называется разложением вектора
называется разложением вектора
![]() по базису
по базису
![]() .
.
Определение.
Если
векторы
![]() образуют базис линейного пространства
L, и вектор x
из L
линейно выражается через векторы в виде
образуют базис линейного пространства
L, и вектор x
из L
линейно выражается через векторы в виде
![]() ,
то числа
,
то числа
![]() называются
координатами вектора x
в базисе
называются
координатами вектора x
в базисе
![]() .
.
36Эвклидово пространство
В пространстве геометрических векторов скалярное произведение было определено в §5. Там же рассмотрены его свойства. Введем теперь понятие скалярного произведения в любом вещественном линейном пространстве.
Определение. Скалярным произведением
двух векторов
![]() и
и
![]() вещественного линейного пространства
называют действительное число
вещественного линейного пространства
называют действительное число
![]() удовлетворяющее следующим четырем
требованиям (аксиомам):
удовлетворяющее следующим четырем
требованиям (аксиомам):
1)![]()
2)![]()
3)![]()
4)![]() если
если
![]()
![]() если
если
![]()
(сравни эти аксиомы со свойствами скалярного произведения в §5).
Вещественное линейное пространство со
скалярным произведением называют
эвклидовым и обозначают
![]() .
.
Замечание. В комплексном линейном
пространстве скалярным произведением
является комплексное число, удовлетворяющее
перечисленным выше аксиомам 2,3,4. Первая
аксиома заменяется на следующую:
![]() где черта означает комплексное сопряжение.
Комплексное линейное пространство со
скалярным произведением называют
унитарным.
где черта означает комплексное сопряжение.
Комплексное линейное пространство со
скалярным произведением называют
унитарным.
Эвклидово пространство
![]() является одновременно нормированным
и метрическим. Норму и метрику в эвклидовом
пространстве вводят следующим образом:
является одновременно нормированным
и метрическим. Норму и метрику в эвклидовом
пространстве вводят следующим образом:
![]() (1)
(1)
![]() (2)
(2)
Можно проверить, что все аксиомы для нормы и расстояния выполняются.
Приведем некоторые примеры эвклидовых пространств.
-
Координатное пространство
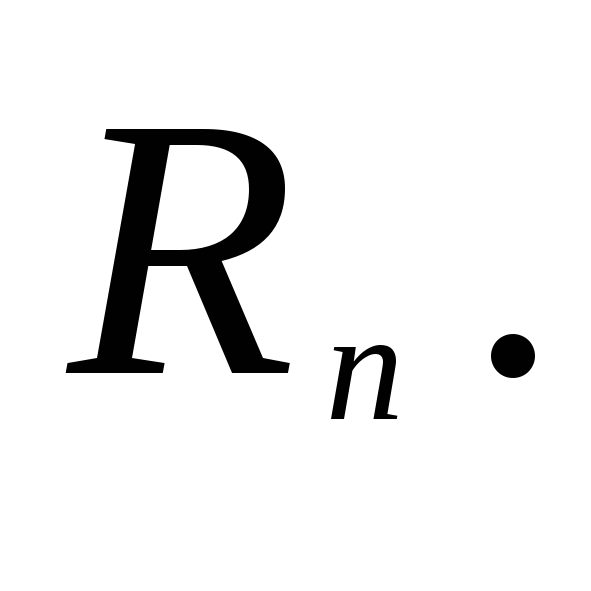
![]() (3)
(3)
 ,
(4)
,
(4)
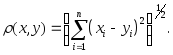 (5)
(5)
-
Пространство непрерывных на отрезке
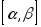 функций
функций
![]() (6)
(6)
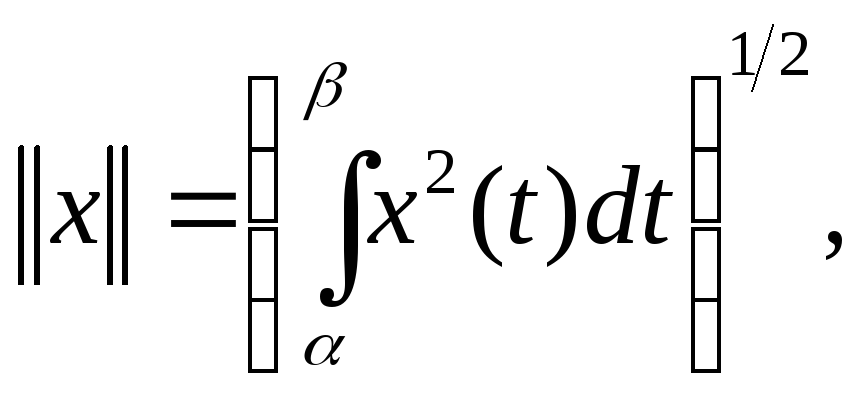 (7)
(7)
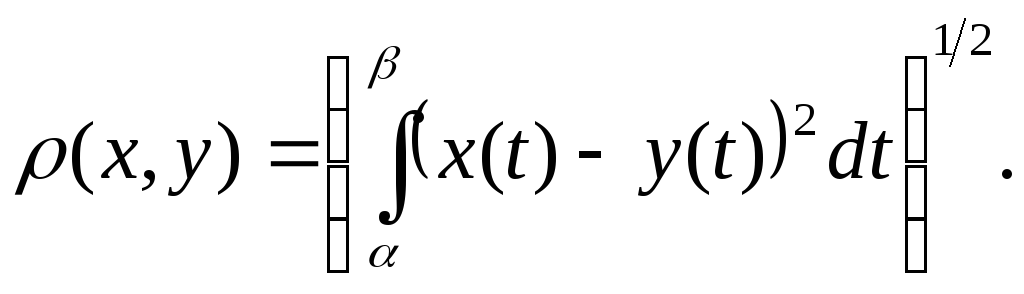 (8)
(8)
-
Пространство многочленов степени не выше

![]()
![]()
![]() (9)
(9)
 (10)
(10)
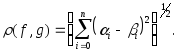 (11)
(11)
Можно проверить, что все аксиомы скалярного произведения выполняются.
Замечание. Не следует думать, что скалярное произведение можно ввести единственным способом. Например, в пространстве многочленов скалярное произведение можно ввести и по формуле (6).
Теорема. В эвклидовом пространстве выполняется неравенство Коши-Буняковского
![]() (12)
(12)
Доказательство. По аксиоме 4 для
всякого
![]() имеем
имеем
![]() (13)
(13)
Используя аксиомы 2, 3, преобразуем левую часть неравенства (13) так:
![]() (14)
(14)
Необходимым и достаточным условием
неотрицательности квадратного трехчлена
(14) является условие, чтобы его дискриминант
не был положительным, т.е.
![]() или
или
![]()
Последнее неравенство совпадает с (12). Теорема доказана.
В линейном пространстве можно ввести
понятие коллинеарности векторов. Если
![]() ,
,
![]() ,
то векторы
,
то векторы
![]() и
и
![]() коллинеарны. Очевидно нулевой вектор
коллинеарны. Очевидно нулевой вектор
![]() коллинеарен любому другому вектору.
Для коллинеарных векторов неравенство
Коши-Буняковского обращается в равенство.
коллинеарен любому другому вектору.
Для коллинеарных векторов неравенство
Коши-Буняковского обращается в равенство.
Кроме коллинеарности в эвклидовом
пространстве можно ввести понятие
ортогональности векторов. Если
![]() то векторы
то векторы
![]() и
и![]() ортогональны.
ортогональны.
Очевидно, нулевой вектор
![]() ортогонален любому другому вектору.
ортогонален любому другому вектору.
Понятие угла между векторами
![]() и
и
![]() в эвклидовом пространстве можно ввести
по формуле
в эвклидовом пространстве можно ввести
по формуле
![]() (15)
(15)
Из неравенства Коши-Буняковского
следует, что
![]() поэтому
поэтому
![]()
Найдем квадрат нормы
![]() (16)
(16)
Равенство (16) с учетом (15) перепишем так:
![]() (17)
(17)
Равенство (17) выражает теорему косинусов.
Если
![]() т.е. векторы
т.е. векторы
![]() и
и
![]() ортогональны, то из (17) получим теорему
Пифагора:
ортогональны, то из (17) получим теорему
Пифагора:
![]() (18)
(18)
Умножив вектор
![]() на величину
на величину
![]() мы можем нормировать любой ненулевой
вектор эвклидового пространства, т.е.
сделать его длину (норму) равной единице.
Поэтому в эвклидовом пространстве можно
ввести понятие ортонормированного
базиса.
мы можем нормировать любой ненулевой
вектор эвклидового пространства, т.е.
сделать его длину (норму) равной единице.
Поэтому в эвклидовом пространстве можно
ввести понятие ортонормированного
базиса.
Базис
![]() называется ортонормированным, если
называется ортонормированным, если
![]() Примером ортонормированного базиса в
эвклидовом пространстве
Примером ортонормированного базиса в
эвклидовом пространстве
![]()
![]() является базис, определяемый формулами
(2) §16. Можно
доказать, что любая система попарно
ортогональных векторов линейно
независимая и любой базис в эвклидовом
пространстве можно ортонормировать.
является базис, определяемый формулами
(2) §16. Можно
доказать, что любая система попарно
ортогональных векторов линейно
независимая и любой базис в эвклидовом
пространстве можно ортонормировать.
