40. Гипербола.

Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек и есть величина постоянная (не равная нулю и меньшая, чем расстояние между и ).

Точки и называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно . Модуль расстояний от точек гиперболы до фокусов и обозначим через . По условию, .

Выбрав декартову систему координат, как в случае эллипса, и используя определение гиперболы, составляем ее уравнение:

(7.6)

где ‑ координаты произвольной точки гиперболы, .

Уравнение (7.6) называется каноническим уравнением гиперболы.

Из уравнения (7.6) видно, что . Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми и .

Так как в уравнение входят только четные степени и , то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем: .

График этой функции от точки уходит неограниченно вправо и вверх (Рис. 7.7), и как угодно близко подходит к прямой:

(7.7)

x

y

O

A(a,0)

Рис. 7.7

Поэтому говорят, что гипербола асимптоматически приближается к прямой (7.7), и эту прямую называют асимптотой гиперболы. Из симметрии гиперболы следует, что у нее две асимптоты .

Построим гиперболу. Сначала строим, так называемый, основной прямоугольник гиперболы, центр которой совпадает с началом координат, а стороны равны и параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 7.8).

Рис 7.8.

Г ипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки и пересечения гиперболы с осью называются вершинами гиперболы. Величины и называются полуосями гиперболы. Если , то гипербола называется равносторонней.

Эксцентриситетом гиперболы называется число . Для любой гиперболы . Эксцентриситет характеризует форму гиперболы: чем меньше, тем больше вытягивается гипербола вдоль оси . На рисунке 7.9 изображены гиперболы с различными значениями .

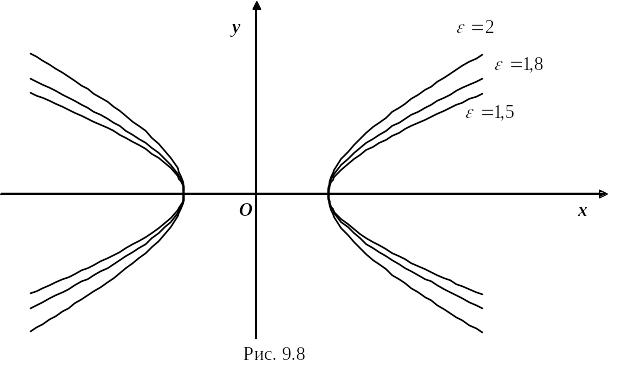
Рис. 7.9

Фокальными радиусами точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами и . Их длины и задаются формулами:

Для правой - ветви ,

Для левой - ветви .

Прямые называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением .

42.Парабола. Параболой называется линия, состоящая из всех точек плоскости, равноудаленных от данной точки (фокуса) и данной прямой (директрисы).

Для вывода канонического уравнения параболы ось проводят через фокус перпендикулярно директрисе в направлении от директрисы к фокусу; начало координат берут в середине отрезка между фокусом и точкой пересечения оси с директрисой . Если обозначить через расстояние фокуса от директрисы, то 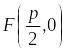и уравнение директрисы будет иметь вид .

В выбранной системе координат уравнение параболы имеет вид:

(7.8)

Это уравнение называется каноническим уравнением параболы. Из уравнения (7.8) видно, что может принимать только неотрицательные значения. Значит, на рисунке вся парабола располагается справа от оси . Так как уравнение (7.8) содержит только в четной степени, то парабола симметрична относительно оси _, и поэтому достаточно рассмотреть ее форму в первой четверти. В этой четверти .

При неограниченном возрастании неограниченно растет и . Парабола, выходя из начала координат, уходит неограниченно вправо и вверх, четвертой четверти парабола строится по симметрии.

С

y



делаем рисунок п араболы (Рис. 7.10).

x

O

Рис.

7.10

Рис.7.10

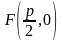
Ось симметрии параболы называется ее осью. Точка пересечения с ее осью называется вершиной параболы.

42.Первообразная и неопределенный интеграл.Интегрирование – операция, обратная дифференцированию, которая позволяет определять функцию , для которой заданная функция является ее производной:

.

Другими словами, если операция дифференцирования состоит в нахождении производной, то интегрирование – это операция отыскания первообразной.

Функция называется первообразной для функции , на промежутке , если для каждой точки этого промежутка .

Теорема. Если и – любые две первообразные для данной функции на промежутке , то для всех выполняется равенство .

Доказательство:

.

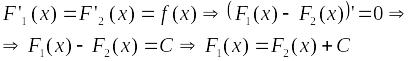43. Основные свойства неопределенного интеграла.1.Производная неопределенного интеграла равна подынтегральной функцией:

1. 

Эти свойства означают, что интегрирование и дифференцирование – взаимно обратные операции.

2. Если и – интегрируемые функции, т.е. на промежутке они имеют первообразные, то сумма функций также интегрируема и .

3. Если – интегрируемая функция, а постоянная величина, то 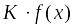– также интегрируемая функция и .

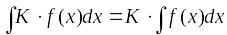Таким образом, свойства 3 и 4 указывают на линейность операции интегрирования:

,

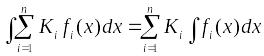где постоянные;

интегрируемые функции.

4. Если , а также 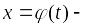дифференцируемая функция, то

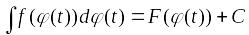
Таким образом, все семейство первообразных для данной функции имеет вид , где одна из первообразных, а произвольная постоянная.

Совокупность всех первообразных для функции на промежутке называется неопределенным интегралом функции .

Неопределенный интеграл обозначается следующим образом:

,

где знак интеграла;

подынтегральная функция;

подынтегральное выражение.