3. Динамика гармонического осциллятора

Пусть пружинный маятник совершает колебания малой амплитуды около положения устойчивого равновесия под действием возвращающей силы упругости, обусловленной деформацией пружины х (рис. 2). При малых деформациях закон силы упругости подчиняется линейному закону Гука F_x =  kx. В отсутствии трения движение описывается линейным дифференциальным уравнением m =  kx (второй закон Ньютона). Это уравнение можно записать в виде + x = 0 . Отношение = имеет размерность квадрата частоты и является собственной характеристикой пружинного маятника (т.к. определяется собственной жесткостью пружины и массой маятника). Итак, уравнение примет вид: + x = 0

Уравнение можно записать в более компактной форме с использованием стандартной записи производной по времени  :

(3)

Решением уравнения (3) является гармоническая функция: x(t) = A cos(₀t + ). Из решения видно, что, действительно, ₀ = имеет смысл собственной циклической частоты. Период собственных колебаний T₀ = =

Пружинный маятник, совершающий гармонические колебания около положения равновесия под действием возвращающей силы вида F_x =  kx, является примером гармонического осциллятора. В конкретной колебательной системе возвращающая сила по своей природе не обязательно должна быть именно силой упругости. Приведем пример.

Опишем свободные колебания ареометра, помещенного в жидкость (рис. 3). Пусть вязкое трение в жидкости отсутствует. На ареометр массой m действует сила тяжести и сила Архимеда.

Рис. 3

Если слегка притопить ареометр на глубину x, то сила Архимеда возрастет по модулю на величину F = Sxg , где S - площадь поперечного сечения отростка ареометра,  - плотность жидкости. Понятно, что при всплытии ареометра выше положения равновесия сила тяжести будет на ту же величину F = Sxg больше силы Архимеда. Сила Архимеда направлена против направления смещения ареометра, т.е. F_x = Sxg, и играет роль возвращающей силы (в пружинном маятнике эту роль играет сила упругости). Второй закон Ньютона в проекции на ось 0Х имеет вид m =  Sxg. После соответствующих преобразований дифференциальное уравнение примет вид:

или ,

где - квадрат собственной частоты колебаний ареометра в жидкости. Решением уравнения является уравнение гармонических колебаний x = A cos (₀t + ), где A = X_max – амплитуда колебаний ареометра.

Динамические уравнения колебаний пружинного маятника и ареометра и их решения имеют одинаковый вид. Роль возвращающей силы в пружинном маятнике играет сила упругости F_x =  kx. Для ареометра возвращающей силой является сила Архимеда, которая формально имеет тот же вид, что и сила упругости: F_x = Sgx =  bx, где b = Sg. В этой связи, возвращающие силы вида F =  bx получили название квазиупругих сил (приставка «квази-» - от латинского quasi – «якобы, как будто, вроде»), т.е. сил, формально схожих с упругой силой.

В качестве иллюстрации сказанного приведем без детализации вывода динамические уравнения и собственные частоты двух других гармонических осцилляторов (рис. 4). Решения этих уравнений имеют одинаковый вид: x = A cos (₀t + ),.

Математический маятник:

J =  mgl, где J = ml ² – момент инерции маятника.

Собственная частота , период T = = .

Рис.4-а Решение уравнения:  = _max cos (₀t + ).

К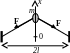 олебания материальной точки m, прикрепленной к двум стру-

нам: m = 

Собственная частота , период T₀ = = .

Рис. 4-б Решение уравнения: x = X_max cos (₀t + ).

Во некоторых случаях динамику осциллятора удобно описывать не на языке сил, а на языке энергии. Так поступают, например, при описании динамики квантовых осцилляторов с опосредованным использованием понятия квазиупругой силы. Действительно, в положении равновесия потенциальная энергия осциллятора U(x) имеет минимум. При малых колебаниях, т.е. при малых амплитудах А, потенциальная энергия гармонического осциллятора имеет вид U(x) = , тогда для малых колебаний квазиупругая сила примет вид: F = =  kx. В квантовой механике динамику линейного квантового осциллятора решают с помощью уравнения Шредингера, где динамической переменной является не сила, а энергия. Потенциальная энергия осциллятора имеет тот же вид, что и в классическом механическом осцилляторе, т.е. U(x) = . При этом оказывается, что решение уравнения Шредингера существует лишь при дискретных значениях полной энергии квантового осциллятора. Напомним, полная энергия Е классического гармонического осциллятора может принимать любые значения и равна сумме колеблющихся в противофазе потенциальной U и кинетической энергии E_k осциллятора: E = U + E_k, причем

E = = .