2.4. Динамика вынужденных колебаний. Импеданс колебательной системы

Вследствие потери энергии свободные колебания осциллятора являются затухающими. Для генерации незатухающих колебаний необходимо эти потери компенсировать. Например, затухание колебания качели можно компенсировать, если в нужный моменты времени подталкивать качели. В данном примере внешняя вынуждающая сила является импульсной силой. Рассмотрим вынужденные колебания пружинного маятника под действием непрерывной гармонической вынуждающей силы F_x(t) = F₀ cost, где  - частота внешней вынуждающей силы (рис.12).

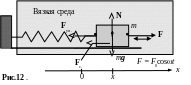
На колеблющееся тело маятника действуют сила сопротивления среды F_c. = v_x =   (примером является сила Стокса F = 6Rv) и сила упругости пружины F_уп. =  kx. Второй закон Ньютона имеет вид: , или в компактной записи

, (6)

где ; . Уравнение 2-го закона Ньютона (6) является линейным неоднородным (с правой частью f(t) = ) дифференциальным уравнением второго порядка с постоянными коэффициентами 1, 2, и .

Известно, что решение неоднородного уравнения равно сумме общего решения однородного уравнения (т.е. уравнения ) и частного решения неоднородного уравнения. Общее решение уравнения нами найдено в предыдущем параграфе: x = A e ^{ t} cos (^/t + ). Частота затухающего члена обозначена через ^/, которая отличается от частоты внешней вынуждающей силы . С течением времени этот член в решении неоднородного уравнения затухает и не вносит вклад в характер колебания материальной точки. Установившаяся часть вынужденных колебаний определяется частным решением неоднородного уравнения.

Математическое приложение

В теории дифференциальных уравнений рассматривается прием нахождения частного решения линейного неоднородного уравнения с постоянными вещественными коэффициентами ( в уравнении (6) этими коэффициентами являются 1, 2, и ). Этот прием заключается в том, что вначале находится решение соответствующего неоднородного дифференциального уравнения от комплексной функции, и далее из этого решения выделяется действительная часть, которая и будет решением исходного дифференциального уравнения. Остановимся подробнее на этом приеме.

Имеется некоторое неоднородное дифференциальное уравнение: , где С, D - вещественные постоянные коэффициенты; f(t) и (t) - вещественные функции; - мнимая единица. Функция z(t) является комплексной: z(t) = x(t) + iy(t), где x(t) и y(t) - вещественные функции. Комплексной функцией является и правая часть уравнения. После подстановки z(t) = x (t) + iy (t) в уравнение получим:

+ i( ) = .

Т.к. два комплексных числа равны, если равны по отдельности их действительная и мнимая части, то: = f (t) и = .

Из приведенных соотношений следует суть рассматриваемого приема для нахождения частного решения неоднородного дифференциального уравнения:

1) к правой части решаемого уравнения = f(t) прибавляется мнимая функция . При этом получается уравнение в комплексной форме . Решением уравнения является комплексная функция z(t) = x (t) + iy (t);

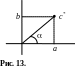2) Из этого решения выделяется действительная часть x(t), которая и является решением уравнения = f(t). Выбор функции диктуется видом функции f(t) в соответствии с формулой Эйлера: если f(t) - функция косинуса, то в качестве принимается функция синуса.

Напомним также, что модуль c произвольного комплексного числа с = a + ib в комплексной плоскости выражается теоремой Пифагора:

с = (рис. 13).

Т.к. cos  = и sin  = , то с = a + ib можно представить через модуль в виде: с = a + ib = c cos  + i c sin  = c (cos  + i sin ) = exp (i).

Перейдем к нахождению частного решения дифференциального уравнения (6). Прибавим к правой части (6) мнимую функцию (i ), получим:

, или, по формуле Эйлера (§ 2.3),

. (7)

Искомой комплексной функцией является z(t) = x (t) + iy (t). В качестве решения выберем функцию z(t) = Аexp (it), где А - комплексное число. Определим комплексную амплитуду, для чего подставим z(t) в уравнение (7):

[  ²A + i2A + A] exp (it) = exp (it).

Т.к. данное уравнение выполняется при всех t , то А = . Умножим числитель и знаменатель на мнимую единицу со знаком минус (i), а также учтем, что , : А = = , где

(8)

называется механическим импедансом в комплексной форме (от латинского -impedire - препятствовать), или полным механическим сопротивлением в комплексной форме. Комплексный импеданс как любое комплексное число можно выразить в виде:

* = (cos + icos) =  exp(i).

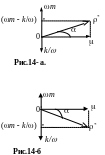Смысл фазы  следует из представления ^* в комплексной плоскости (рис. 14-а,б). Модуль комплексного импеданса

 =

называется механическим импедансом или полным механическим сопротивлением.

При низких частотах вынуждающей силы m < . В этом случае фаза  имеет отрицательное значение (рис. 14-б) и при   0 фаза стремится к значению    . При высоких частотах m > . В этом случае фаза  положительна (рис. 14-а) и при    фаза   . При m = фаза равна нулю. В этом случае импеданс определяется только действительной составляющей  = .

Механический импеданс  = аналогичен электрическому импедансу для цепи переменного тока Z = . Масса m аналогична индуктивности L электрической цепи, обратная величина жесткости пружины аналогична электрической емкости С цепи. По аналогии с электрической цепью выражение (m  ) называется реактивной частью механического импеданса, а коэффициент трения  - активной частью импеданса. Активная часть  механического импеданса  определяет диссипацию механической энергии колебательной системы - безвозвратные потери механической энергии. Реактивная часть (m  ) связана с механической энергией колебательной системы: с кинетической энергией материальной точки и потенциальной энергией деформированной пружины. Единица механического импеданса в СИ: 1 . Угол  = 0 при выполнении равенства m = . В следующем параграфе вернемся к понятию импеданса.

Итак, искомая комплексная функция z(t) = Аexp(it) приобретает вид:

z(t) = Аexp(it) = exp(it) = exp(it).

Так как = exp [i(t  )] , то

z(t) = exp [i(t  )]. (9)

Выражение (9) и есть решением комплексного уравнения (7).

Представим комплексное решение (9) в стандартной форме z(t) = x (t) + iy (t):

z(t) = sin (t  )  i cos (t  ).

Действительная часть решения:

x (t) = sin (t  ) = Хsin (t  ),

где Х = = 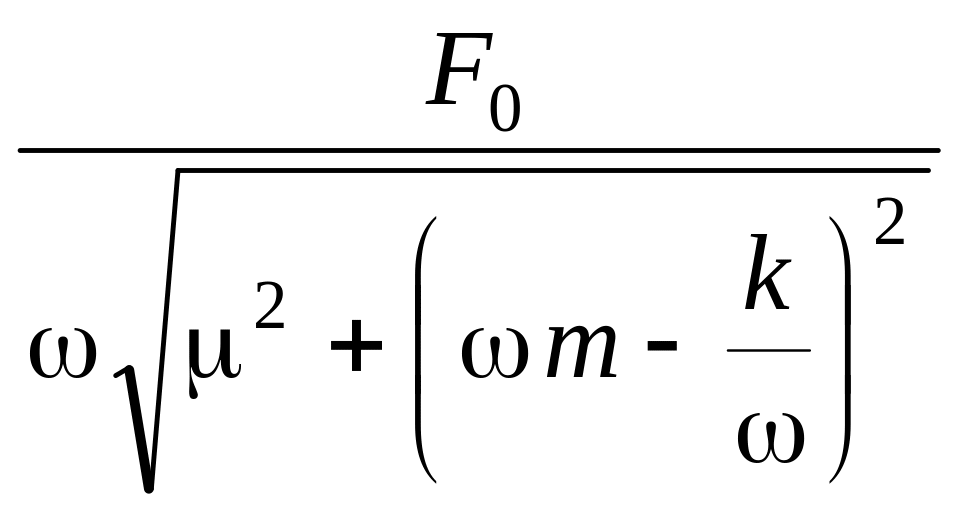(10)

модуль комплексной амплитуды A является действительным числом и называется просто амплитудой смещения маятника при установившемся режиме вынужденных колебаний.

Амплитуда устоявшихся вынужденных колебаний (10) зависит: 1) от собственных свойств осциллятора - k и m; 2) вязких свойств среды , в которой осциллятор совершает колебания; 3) частоты  и амплитуды F₀ внешней вынуждающей силы F_x(t) . Данный вывод подтверждается в эксперименте. Так как и , то амплитуду (10) можно выразить через  и ₀, подставив эти значения в (10):

Х = = 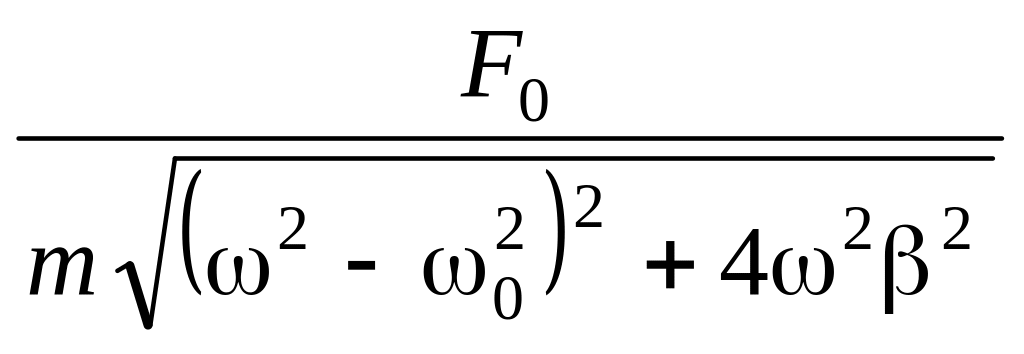. (11)

Итак, частное решение в тригонометрической форме имеет вид:

x(t) = Хsin (t  ) или (12*)

x(t) = Хcos (t  ). (12**)

где  =  + . На рис. 15 приведен график колебаний при двух разных значения коэффициента затухания , причем ₁>₂. В этом случае амплитуды вынужденных колебаний соотносятся как X₁ < X₂.