
- •1Вопрос.
- •2Вопрос.
- •3. Действия над событиями. Сложение событий. Сложные события.
- •4. Теорема сложения вероятностей. Следствия.
- •Вопрос 5.
- •Вопрос 6.Формула полной вероятности:
- •7. Формула Байеса
- •Вопрос 9.
- •Вопрос 10.
- •Вопрос 13.Характеристики случайной величины: центральный момент и дисперсия
- •Вопрос14.
- •15. Законы распределения – равномерный, показательный.
- •Вопрос 17:
- •Вопрос 18.Числовые характеристики системы двух случайных величин. Начальные, центральные моменты.
- •1,1-Называет ковариацией и обозначают cou(x1;x2).
- •19. Корреляционный момент. Коэффициент корреляции.
- •20. Уравнение линейной регрессии. Коэффициент линейной регрессии.
- •Вопрос 21.
- •Вопрос 22.
Вопрос 17:
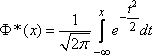 данная функция представляет собой,
функцию распределения для нормально
распределенной случайной величины с
параметрами
данная функция представляет собой,
функцию распределения для нормально
распределенной случайной величины с
параметрами![]()
Условимся называть функцию нормальной функцией распределения.
вероятность
попадания случайной величины х на
интервале от а до в:![]()
Таким
образом, мы выразили вероятность
попадания на участок случайной величины
х, распределенной по нормальному закону
с любыми параметрами, через стандартную
функцию распределения
![]() , соответствующую простейшему нормальному
закону с параметрами 0,1. Заметим, что
аргументы функции
, соответствующую простейшему нормальному
закону с параметрами 0,1. Заметим, что
аргументы функции![]() в данной формуле имеют очень простой
смысл:
в данной формуле имеют очень простой
смысл:![]() есть расстояние от правого конца участка
есть расстояние от правого конца участка![]() до центра рассеивания, выраженное в
средних квадратических отклонениях;
до центра рассеивания, выраженное в
средних квадратических отклонениях;![]() - такое же расстояние для левого конца
участка, причем это расстояние считается
положительным, если конец расположен
справа от центра рассеивания, и
отрицательным, если слева.
- такое же расстояние для левого конца
участка, причем это расстояние считается
положительным, если конец расположен
справа от центра рассеивания, и
отрицательным, если слева.
Свойства функции:
1.![]()
![]()
2.![]()
3.![]() -
не убывающая функция.
-
не убывающая функция.
Кроме того,
из симметричности нормального
распределения с параметрами
![]() относительно начала координат следует,
что
относительно начала координат следует,
что![]() .
.
На практике
часто встречается задача вычисления
вероятности попадания нормально
распределенной случайной величины на
участок, симметричный относительно
центра рассеивания
![]() . Рассмотрим такой участок длины
. Рассмотрим такой участок длины![]() . Вычислим вероятность попадания на
этот участок по формуле
. Вычислим вероятность попадания на
этот участок по формуле![]() получим:
получим:
![]()
Учитывая свойства функции
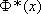 ,данная
формула примет более компактный вид,
получим формулу для вероятности
попадания случайной величины,
распределенной по нормальному закону
на участок, симметричный относительно
центра рассеивания:
,данная
формула примет более компактный вид,
получим формулу для вероятности
попадания случайной величины,
распределенной по нормальному закону
на участок, симметричный относительно
центра рассеивания: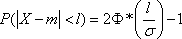
Вопрос 18.Числовые характеристики системы двух случайных величин. Начальные, центральные моменты.
Начальным смешанным моментом порядка(i,k),двумерной случайной величины (х1,х2)называется число
 i,k
следовательно
i,k
следовательно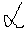 i,k=M[x1i;x2j]
i,k=M[x1i;x2j]
Найти начальный смешанный момент порядка (1;0)
![]() 1,0=М[x11;x20]=M[x1]
1,0=М[x11;x20]=M[x1]
Центральным смешанным моментом порядка (i,k)случайной велечены (х1;х2) называется число
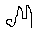 i,k=М[([1-mx1)i*(x2-
mx2)K]
i,k=М[([1-mx1)i*(x2-
mx2)K]
![]() 2,0=
М[([1-mx1)2*(x2-
mx2)0]=D[x1]
2,0=
М[([1-mx1)2*(x2-
mx2)0]=D[x1]
![]() 0,2=
М[([1-mx1)0*(x2-
mx2)2]=D[x2]
0,2=
М[([1-mx1)0*(x2-
mx2)2]=D[x2]
Особую роль имеет центральный смешанный момент порядка (1;1)
![]() 1,1=
М[([1-mx1)1*(x2-
mx2)1]=математическое
ожидание произведения центрированных
величин х и у.
1,1=
М[([1-mx1)1*(x2-
mx2)1]=математическое
ожидание произведения центрированных
величин х и у.
1,1-Называет ковариацией и обозначают cou(x1;x2).
19. Корреляционный момент. Коэффициент корреляции.
Чтобы привести ковариация (cov) к линейным единицам измерения, нормируют cov Коэффициент корреляции Корреляция, это степень зависимости между двумя случайными величинами X и Y. Для исследования подобных зависимостей пользуются конечным (выборочным) набором пар значений (x1 , y1) , (x2 , y2) ,…, (xn , yn)
где xk — k-е значение случайной величины Х, а yk — соответствующее ему значение случайной величины Y. Корреляция - величина, отражающая наличие связи между явлениями, процессами и характеризующими их показателями.
Корреляционная зависимость - определение зависимости средней величины одного признака от изменения значения другого признака.
Коэффициент корреляции величин х и у (rxy) свидетельствует о наличии или отсутствии линейной связи между переменными:
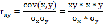
где 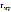
 (-1;
1). Если:
(-1;
1). Если: =
-1, то наблюдается строгая отрицательная
связь;
=
-1, то наблюдается строгая отрицательная
связь;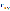 =
1, то наблюдается строгая положительная
связь;
=
1, то наблюдается строгая положительная
связь;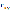 =
0, то линейная связь отсутствует.
=
0, то линейная связь отсутствует.
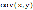 -
ковариация, т. е. среднее произведение
отклонений признаков от их средних
квадратических отклонений.
-
ковариация, т. е. среднее произведение
отклонений признаков от их средних
квадратических отклонений.
Коэффициент корреляции может служить мерой зависимости случайных величин.
