1.3. Число «е»

Числом «е» называется предел последовательности с общим членом .

Применив формулу бинома Ньютона, найдем

Учитывая неравенство , для любого, получими,

где – сумма бесконечно убывающей геометрической прогрессии,

Получили, что , т.е. предел последовательности – это некоторое число, лежащее на интервале (2;3).

Это число определил Леонард Эйлер (1707 – 1783) – великий математик, член Петербургской Академии наук, большую часть жизни проведший в России, по происхождению швейцарец.

При помощи современных ЭВМ, это число вычислено с точностью до 590 знаков после запятой. Отдавая дань Эйлеру, это число называют числом «е»: е =2,718281…

Число е играет огромную роль в математике.

Рассмотрим примеры.

1. 

2. .

3. .

Предел числовой последовательности. Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении порядкового номера n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение.

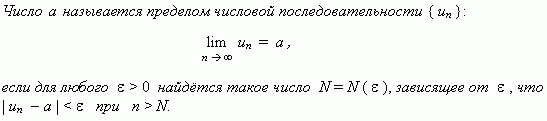
Это определение означает, что a есть предел числовой последовательности, если её общий член неограниченно приближается к a при возрастании n. Геометрически это значит, что для любого > 0 можно найти такое число N, что начиная с n > N все члены последовательности расположены внутри интервала ( a -, a +). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.

1. Применения пределов

1.2.1. Площадь круга

Для вычисления площади круга единичного радиуса опишем вокруг него правильный n-угольник. Его площадь, равная n площадям одинако-вых равнобедренных треугольников с вершинами в т. О, даст приближение площади круга с избытком. Площадь одного треугольника равна произве-дению единичной высоты на половину основания, равную тангенсу угла ; площадьS_n всего n-угольника будет в n раз больше: .

Например, площадь правильного треугольника: ;

площадь описанного квадрата:

площадь описанного шестиугольника:

Монотонно убывающая последовательность S_n сходится к числу - площади круга единичного радиуса.

Последовательность площадей правильных многоугольников, вписанных в окружность, дает приближения площади круга с недостатком. Площадь одного из n равнобедренных треугольников, составляющих вписанный n-угольник, можно вычислить, как половину произведения единичных сторон на синус угла между ними; обозначив черезs_n площадь всего n-угольника, получим монотонно возрастающую последовательность приближений, стремящихся к площади круга снизу:

1.2.2. Объем шара и пирамиды

Для нахождения объема шара и пирамиды построим последователь-ности вписанных в них цилиндров и призм, объемы которых известны ( из очевидных соображений они равны произведению площади основания на высоту).

Разрежем полушарие радиуса R равноотстоящими параллельными плоскостями на n частей и впишем в него n-1 цилиндр. Радиусы основа-ния цилиндров находятся с помощью теоремы Пифагора, объем ступенча-того тела V_n , приближающийся c ростом n к объему полушария преобразуется к виду

Аналогично строится приближение пирамиды с площадью основания S и высотой h вписанными призмами с высотами h/n. Определив площади их оснований из условия подобия, получим объем ступенчатого тела какn-й член последовательности, сходящейся к объему пирамиды.

Позже будет показано, что предел переменной дроби, входящей в оба приближения, равен 1/3:

Используя этот результат, получим точные формулы для вычисления объемов полушария:

и пирамиды:

7. Производная функция. Геометрический смысл производной. Таблица производных.

Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференцированием. Обратный процесс — интегрирование.

Производной функциейв точке x0 называется число, к которому стремится разностное отношениепри Δx, стремящемся к нулю.

Производные элементарных функций

Геометрический смысл производной

Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке

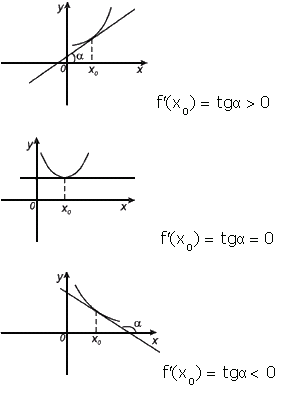
Уравнение касательной к графику функции y = f(x) в точке x0:

Таблица производных основных элементарных функций

1) ; 10);

2) ; 11);

3) ; 12);

4) ; 13);

5) ; 14);

6) ; 15);

7) ; 16);

8) ; 17);

9) ; 18);

19).

7. Свойства производных. Примеры.

Свойства производных функций

1. Производная суммы функций

равна сумме их производных, если они существуют, т. е.

(u+v)’=u’+v’

2. Производная произведения двух функций

вычисляется по формуле (uv)’ = u’v + uv’

в предположении, что производные u’ и v’ существуют.

3. Постоянный множитель можно выносить за знак производной: (kf(x))’ = kf’(x).

4. Производная частного вычисляется по формуле

5. Производная сложной функции

равна произведению ее производной по промежуточному аргументу на производную этого аргумента по независимой переменной:y=f( u(x) ) y’=f’(u).u’(x)

6. Диференциал функции

Произведение производной на произвольное приращение аргумента

является главной частью приращения функции.

Это произведение называется диференциалом и обозначается df(x)=dy=f’(x)dx.

Часто приращение функции заменяют ее диференциалом при приближенных вычислениях.

7. Неопределенный интеграл и его свойства. Таблица интегралов. Примеры.

Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:F(x) + C.

Записывают:

Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.

Свойства:1. 2.3.4.гдеu, v, w – некоторые функции от х.

1. 

Пример:

Нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для некоторых функций это достаточно сложная задача. Ниже будут рассмотрены способы нахождения неопределенных интегралов для основных классов функций – рациональных, иррациональных, тригонометрических, показательных и др.

Таблица основных интегралов.

Для удобства значения неопределенных интегралов большинства элементарных функций собраны в специальные таблицы интегралов, которые бывают иногда весьма объемными. В них включены различные наиболее часто встречающиеся комбинации функций. Но большинство представленных в этих таблицах формул являются следствиями друг друга, поэтому ниже приведем таблицу основных интегралов, с помощью которой можно получить значения неопределенных интегралов различных функций.

Интеграл			Значение		Интеграл			Значение
1		-lncosx+C		9			e^x + C
2		lnsinx+ C		10			sinx + C
3				11			-cosx + C
4				12			tgx + C
5				13			-ctgx + C
6		ln		14			arcsin+ C
7				15
8				16

. Непосредственное интегрирование.

Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.

Рассмотрим применение этого метода на примере: Требуется найти значение интеграла . На основе известной формулы дифференцированияможно сделать вывод, что искомый интеграл равен, где С – некоторое постоянное число. Однако, с другой стороны. Таким образом, окончательно можно сделать вывод:

Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных. Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало.

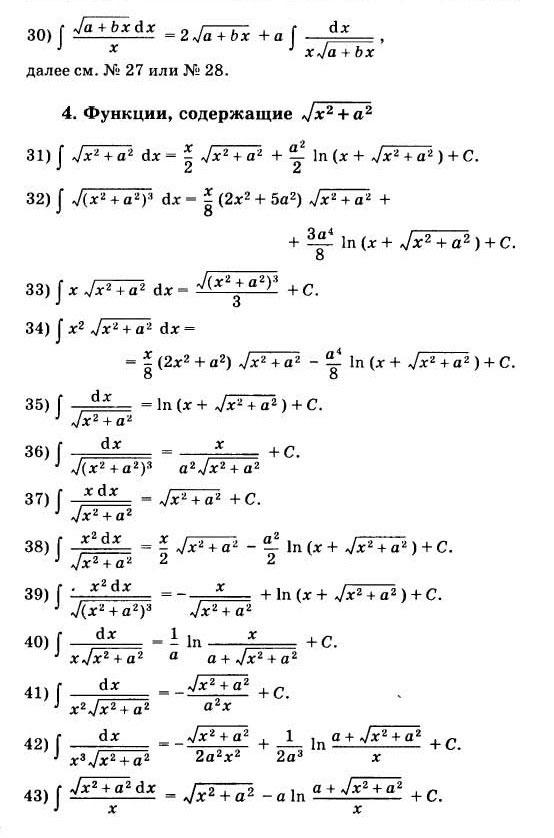
7. Определенный интеграл и его свойства. Геометрический смысл определенного интеграла и его вычисления.

Определённый интеграл, его свойства

Пусть на отрезке задана функцияy=f(x). Разобьем отрезок наn элементарных отрезков точками . На каждом отрезкеразбиения выберем некоторую точкуи положим, где. Сумму вида

будем называть интегральной суммой для функции y=f(x) на . Очевидно, что интегральная сумма зависит как от способа разбиения отрезкаточками, так и от выбора точекна каждом из отрезков разбиения,.

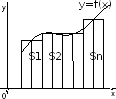
Если существует предел , не зависящий от способа разбиения отрезкаи выбора точек, то этот предел будем называтьопределённым интегралом функции f(x) на отрезке и обозначать символом т.е.

Функция f(x) в этом случае называется интегрируемой на отрезке . При этомf(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением, а числа a и b – пределами интегрирования (a – нижний предел, b – верхний предел), а сумма –интегральной суммой.

Теорема. Если функция f(x) непрерывна на отрезке , то она интегрируема на этом отрезке.

Свойства определённого интеграла

1.

2. Постоянный множитель можно выносить за знак определённого интеграла:

3. Определённый интеграл от суммы двух функций равен сумме определённых интегралов от этих функций:

4. При перестановке пределов интегрирования определённый интеграл меняет знак на противоположный:

5. Интеграл по отрезку равен сумме интегралов по его частям: гдеa<c<b.

6. Теорема об оценке интеграла

Если для , тогда значения интеграла от этой функции не менее произведения m на длину отрезка и не более произведения M на длину отрезка.

7. Теорема о среднем значении

Если f(x) непрерывна на отрезке , то существует такое значение, чтоf(x₀)=f_ср – среднее значение f на отрезке.