§1. Понятие случайной величины. Закон распределения случайной величины

Одним из важнейших понятий теории вероятностей (наряду со случайным событием и вероятностью) является понятие случайной величины.

Случайной величиной называется величина, которая в результате опыта принимает то или иное числовое значение, причем заранее, до опыта, неизвестно, какое именно.

Случайные величины обозначаются заглавными буквами латинского алфавита – ,,, …, а принимаемые ими значения - соответствующими малыми буквами.

Случайная величина, принимающая конечное или счетное множество значений: называется дискретной или прерывной случайной величиной.

Непрерывной случайной величиной называется случайная величина, бесконечное несчетное множество возможных значений которой есть некоторый промежуток (конечный или бесконечный) числовой оси. (Строгое определение непрерывной случайной величины будет дано ниже).

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Закон распределения дискретной случайной величины. Многоугольник распределения

Закон распределения может иметь разные формы. Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически.

Простейшей формой задания закона распределения дискретной случайной величины X является таблица (матрица), в которой в порядке возрастания перечислены все возможные значения случайной величины и соответствующие их вероятности, т.е.

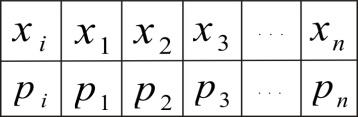
или , где;.

Такая таблица называется рядом распределения дискретной случайной величины X.

Графическое изображение ряда распределения (см. рис.1) называется многоугольником (или полигоном) распределения.

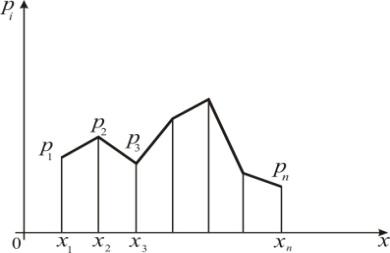
Рис. 1

Математическое ожидание. Дисперсия и среднее квадратическое отклонение случайной величины

Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Однако при решении многих практических задач достаточно знать лишь некоторые числовые параметры, выражающие наиболее характерные свойства (черты) закона распределения случайной величины. Такие числа носят название числовых характеристик случайной величины.

Математическим ожиданием (или средним значением) (или ) дискретной случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности этих значений.

Если дискретная случайная величина X принимает конечное число значений , то ее математическое ожиданиенаходится по формуле(3)

Если же дискретная случайная величина X принимает бесконечное (счетное) число значений, то , (4) при этом математическое ожидание существует, если ряд в правой части этой формулы абсолютно сходится, т. е. сходится ряд.

Математическое ожидание непрерывной случайной величины X с плотностью вероятности,находится по формуле, (5)

при этом математическое ожидание существует, если интеграл в правой части равенства абсолютно сходится (это значит, что сходится интеграл ).

Дисперсией (рассеянием) (или) случайной величиныназывается математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: .

Из определения вытекает часто используемая формула: .

Если - дискретная случайная величина, то ее дисперсия вычисляется по формуле:, (т. е.) (6) в случае конечного числа значений, принимаемых случайной величиной X, и по формуле , (т. е.) (7) в случае счетного числа значений.

Если X-непрерывная случайная величина с плотностью , то(или). (8)

Средним квадратическим отклонением случайной величины называется величина.

Среднее квадратическое отклонение есть мера рассеяния значений случайной величины около ее математического ожидания.

7. Формула Бернулли вычисления вероятности. Математическое ожидание и дисперсия в этом случае. Примеры.

Формула Бернулли.

Производятся n независимых испытаний, в каждом из которых может произойти некоторое событие А (по традиции такой исход опыта называется успехом) с одной и той же вероятностью или произойти противоположное событие А (такой исход называют неудачей) с вероятностью. Тогда вероятность того, что событие А наступит ровно m раз, находится по формуле Бернулли

в частности, следует, что вероятность того, что в n испытаниях, удовлетворяющих схеме Бернулли, событие А наступит:

1)менее раз — равна

2)более раз — равна

3) хотя бы один раз — равна

4) не менее раз и не болеераза — равна:

Число называетсянаивероятнейшим числом наступлений (или наиболее вероятным числом успехов) в схеме Бернулли, если вероятности p и q отличны от нуля то число можно найти из двойного неравенства

Если в каждом независимом испытании вероятность наступления события А равна (числа разные ), то вероятностьтого, что в этой серии испытаний событие А наступит m раз , равна коэффициенту при m – ой степени многочлена

функция называется производящей функцией

Пример1.Игральную кость подбрасывают 10 раз. Найти вероятность того, что шестерка выпадет:

1. ровно 2 раза; b) не более 8 раз; c) хотя бы один раз

Решение:

Проводится 10 независимых испытаний. Каждое испытание имеет два исхода: выпадет шестерка, не выпадет шестерка. Вероятность выпадения шестерки в каждом испытании постоянна и равна . Таким образом, мы имеем дело со схемой испытаний Бернулли. Для нахождения искомых вероятностей используем схему Бернулли.

1. Здесь Отсюда,b) Искомая вероятность равна:

Однако в этом случае удобно найти вероятность противоположного события – «шестерка выпадет более 8 раз» т.е. 9 или 10

Итак, вероятность того, что шестерка выпадет не более 8 раз, равна

2. Искомая вероятность равна

Пример 2.Всхожесть семян данного сорта растений составляет 70%. Найти наивероятнейшее число всхожих семян в партии из 240 семян.

Решение:Наивероятнейшее число находим из двойного неравенства

Поскольку , то

Отсюда следует, что

Ответ: 168

Пример 3.Прибор состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента за время равны. Найти вероятность того, что откажут два элемента.

Решение:Так как , то вероятность того, что элемент не откажет равны. Составим производящую функцию :

Отсюда следует, что