2 курс 2 семестр

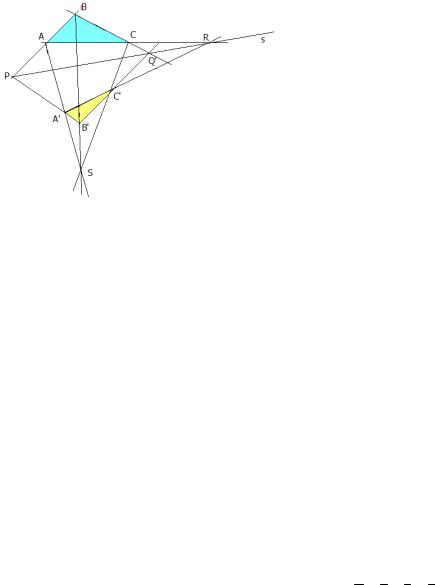
БДПУ імя М.Танка

матэматычны факультэт

кафедра алгебры і геаметрыі

трохвяршыннікам. Пункты А,В,С называюцца вяршынямі, а прамыя АВ, ВС, АС – старанамі трохвяршынніка.

ТЭАРЭМА (Дэзарга) Няхай два

трохвяршыннікі АВС і А’В’С’ размешчаны так,

што ніводная з вяршынь альбо старон аднаго з іх не

супадае з адпаведнымі элементамі другога. Тады,

калі тры прамыя АА’, ВВ’, СС’, якія злучаюць

адпаведныя вяршыні

гэтых трохвяршыннікаў,

праходзяць праз адзін пункт S, то тры пункты

P,Q,R перасячэння іх адпаведных старон ляжаць на

адной прамой.

Заўважым, што трохвяршыннікі могуць

належыць адной або розным пласкасцям.

Дадзена: S= ' ', S CC'. Пункты А, А’,S - ляжаць на адной прамой. Таму

вектары

ā ,ā’,

, якія выклікаюць іх, кампланарныя '

не паралельны

' . Значыць,

s

a

а

11

'

'(1). Аналагічным чынам будзе

s

a

a

'

' (2)

s

b

b

a b 'b' 'a' p (4)q,r

s c 'c' (3).

Адымаючы з першай роўнасці другую, з другой трэцюю, з трэцяй першую роўнасць, і

абазначаючы рознасці праз

p

,

, атрымаем

(5)

'

' '

'

b

c

c

b

q

'

' '

'

(6)

c

a

a

c

r

не паралельны

. Аналагічным чынам

a

b

p

0

q

0,r 0. Вобразамі вектараў

,

,

з’яўляюцца адпаведна пункты P, Q, R. (4) P AB,P A'B' P AB A'B'.

p

q

r

Аналагічным чынам

Q BC B'C'

R AC A'C', p q r 0 .

З гэтага вынікае, што пункты P, Q, R належаць адной прамой.

Тэарэма даказана як для плоскасці, так і для трохмернай праектыўнай прасторы.

Адваротная тэарэма Дэзарга: Няхай два трохвяршыннікі АВС і A’B’C’ размешчаны так, што ніводная з вяршынь або старон адного з іх не супадае з адпаведным элементам другога. Тады, калі тры пункты P,Q,R перасячэння адпаведных старон гэтых трохвяршыннікаў належаць адной прамой s, то тры прамыя АА’ , ВВ’, СС’, якія злучаюць адпаведныя іх вяршыні, праходзяць праз адзін пункт S.

На плоскасці адваротная тэарэма выконваецца поводле прынцыпа дваіснасці. У прасторы яе можна даказаць метадам, аналагічным як і пры доказе прамой тэарэмы на плоскасці.

Пункт S называецца цэнтрам перспектывы трохвугольнікаў ∆АВС і ∆А’В’С’, а прамая s=PQ – называецца воссю перспектывы.

Тэарэму Дэзарга можна коратка сфармуляваць так: два трохвугольнікі ∆АВС і ∆А’В’С’ маюць цэнтр перспектывы тады і толькі тады, калі яны маюць вось перспектывы.

	БДПУ імя М.Танка		матэматычны факультэт	кафедра алгебры і геаметрыі
	§10. Праектыўныя адвображанні і пераўтварэнні плоскасцей.
	Дадзены две праектыўныя плоскасці і '.
	Азначэнне: Няхай у плоскасці зададзены праектыўны рэпер R і ў гэтым рэперы
	пункт М(х1,х2,х3). На плоскасці ' зададзены праектыўны рэпер R’. Паставім ў
	адпаведнасць пункту М пункт М’ ', які ў рэперы R’ мае гэтыя самыя праектыўныя
	каардынаты (х1,х2,х3), г.зн. М’(х1,х2,х3) у рэперы R’.
	Атрымаем узаемнаадназначнае адвображанне f : '. Яно называецца
	праектыўным адвображаннем плоскасці на плоскасць '.
	Пры гэтым адвображанні мноства пунктаў М (хі), каардынаты якіх задавальняюць
	аднароднаму раўнанню першай ступені аіхі=0 (1) (і=1,2,3) пераходзіць у мноства пунктаў,
	каардынаты якіх задавальняюць таму самаму раўнанню (1). Яно вызначае на праектыўнай
	плоскасці прамую.
	Такім чынам, пры праектыўным адвображанні адной плоскасці на другую ўсялякая
	прамая пераходзіць у прамую.
	Таму часам праектыўнае адвображанне вызначаюць, як адвображанне адной
	плоскасці на другую, пры гэтым кожная прамая пераходзіць у прамую.
	Няхай дадзены два праектыўныя рэперы, назавем умоўна стары рэпер R=(A1;A2;A3;E),
	і новы R’=(A1’;A2’;A3’;E’).
	У адпаведных рэперах каардынатныя пункты маюць каардынаты.
12	У рэперы R	А1(1;0;0), А2(0;1;0), А3(0;0;1), Е(1;1;1).
	У рэперы R’	А1’(1;0;0), А2’(0;1;0), А3’ (0;0;1), Е’(1;1;1).
	Паводле азначэння праектыўнага адвображання маем: А’і=f(Ai), E’=f(E) i=(1,2,3)
	Мы прыходзім да высновы: калі на праектыўных пласкасцях і ' зададзены
	адпаведна праектыўныя рэперы R і R’ , то гэтым вызначаецца адзінае праектыўнае
	адвображанне f	: '	, якое пераводзіць рэпер R у рэпер R’.
	Праектыўнае адвображанне адной праектыўнай плоскасці на другую можа быць
	зададзена дзвюма ўпарадкаванымі чацверкамі пунктаў, з якіх кожныя тры не ляжаць на
	адной прамой.
	Азначэнне: праектыўнае адвображанне праектыўнай плоскасці на сябе называецца
	праектыўным пераўтварэннем плоскасці.
	Яно вызначаецца парай адпаведных праектыўных рэпераў.
	Усе аналагічна і для праектыўных пераўтварэнняў і адвображанняў прамых.
	Напрыклад, праектыўнае пераўтварэнне прамой вызначаецца дзвюма ўпарадкаванымі
	адпаведнымі тройкамі яе розных пунктаў.
	Нагадаем яшчэ, што праектыўнае пераўтварэнне плоскасці пераводзіць пункт у пункт,
	прамую ў прамую з захаваннем дачынення інцыдэнтнасці. Таму праектыўныя
	пераўтварэнні плоскасці называецца яшчэ інакш калінеацыямі (захоўваецца
	калінеарнасць, г.зн. сулінейнасць пунктаў прамой).
	Далей выведзем аналітычныя выразы праектыўных пераўтварэнняў плоскасці.
	Няхай пераўтварэнне f плоскасці пераводзіць рэпер R у адпаведны рэпер R’. Рэпер
	R’=(A1’;A2’;A3’;E’) зададзены ў рэперы R каардынатамі пунктаў А’і (С1і,С2і,С3і) прычым
	det║cij║ 0.
	Пункт М ( xi ) у рэперы R. Тады яго вобраз М’= f(M) мае ў рэперы R’ гэтыя самыя
	каардынаты паводле азначэння праектыўнага пераўтварэння.
	Абазначым каардынаты вобраза М’ у старым рэперы R праз уі .
	Паводле формул пераўтварэння праектыўных каардынат для пункта М’ старыя яго
	каардынаты выражаюцца праз новыя формуламі yi cij xj			(1) (i,j=1,2,3).
	Тут матрыца ║cij ║ з’яўляецца транспанаванай з матрыцы каардынат пунктаў Аі’
	новага рэпера у старым рэперы R.

БДПУ імя М.Танка

матэматычны факультэт

кафедра алгебры і геаметрыі

Можна даказаць адваротнае (гл. Атанасян Л.С., Базылеў В.Т. “Геаметрыя 2”).

Таму роўнасці (1)- гэта аналітычныя выразы праектыўнага пераўтварэння плоскасці.

Адсюль магчыма сфармуляваць іншае азначэнне праектыўнага пераўтварэння плоскасці.

Гэта такое пераўтварэнне,

якое пункт М ( xi ) пераводзіць у пункт М’(уі), а яго

і

каардынаты у выражаюцца форуламі (1) у адным і тым жа праектыўным рэперы R. У

формулах (1) уі выражаецца лінейнымі аднароднымі функцыямі аргументаў хі. Таму

праектыўныя пераўтварэнні плоскасці называюцца яшчэ інакш лінейнымі аднароднымі

пераўтварэннямі праектыўнай плоскасці.

§11. Група праектыўных пераўтварэнняў плоскасці. Прадмет праектыўнай

геаметрыі.

Мноства ўсіх адвольных пераўтварэнняў плоскасці ўтварае групу адносна кампазіцыі

(паслядоўнага выканання) пераўтварэнняў.

Абазначым гэту групу праз G. Няхай Н – гэта мноства ўсіх праектыўных

пераўтварэнняў праектыўнай плоскасці G.

Няхай f i g – гэта два адвольныя праектыўныя пераўтварэнні, г.зн. f ,g . Будзем

лічыць, што праектыўнае пераўтварэнне f вызначаецца ўпарадкаванай парай адпаведных

13

праектыўных рэпераў (R, R’), г.зн. f : R R'. Дапусцім, што праектыўнае пераўтварэнне

g пераводзіць рэпер R’ у некаторы рэпер R’’. Тады упарадкаваная пара рэпераў (R’, R’’)

адназначна вызначае гэта праектыўнае пераўтварэнне g.

Возьмем цяпер упарадкаваную пару рэпераў (R, R’’). Яна задае праектыўнае

пераўтварэнне, якое з’яўляецца паслядоўным выкананнем спачатку пераўтварэння f, а

пасля пераўтварэння g, г.зн. яно есць кампазіцыя g f .

Такім чынам f ,g g f (1).

Возьмем цяпер упарадкаваную пару рэпераў (R’, R). Яна вызначае некаторае

праектыўнае пераўтварэнне h. Заўважым, што h f - тоеснае пераўтварэнне. Адсюль,

h f 1 - гэта адваротнае пераўтварэнне да пераўтварэння f. Значыць

f

f 1 (2)

З (1)-(2) вынікае, што Н есць падгрупа групы G. Яна называецца праектыўнай групай

плоскасці.

Раздзел геаметрыі, у якім вывучаюцца ўласцівасці фігур праектыўнай плоскасці

інварыянтныя (захоўваюцца нязменнымі) пры кожным праектыўным пераўтварэнні,

называецца геаметрыяй праектыўнай групы або праектыўнай геаметрыяй.

§12. Праектыўныя і перспектыўныя адвображанні прамых і пучкоў.

Пучок прамых есць дваісная фігура прамой.

Праектыўны рэпер ў пучку прамых можа быць зададзены

упарадкаванай тройкай (а1,а2,е) розных прамых пучка.

Кіроўныя вектары

,

прамых а1 і а2 утвараюць базіс

a1

a2

двухмернай вектарнай прасторы.Кіроўны вектар

прамой е :

е

.

e

a1

a2

Няхай

m2

m2

-гэта кіроўны вектар прамой m

пучка Р(О).

m

a1

a2

БДПУ імя М.Танка	матэматычны факультэт	кафедра алгебры і геаметрыі
Азначэнне: Упарадкаваная пара лікаў (m1;m2 ) называецца праектыўнымі
каардынатамі прамой m	у пучку Р(0).
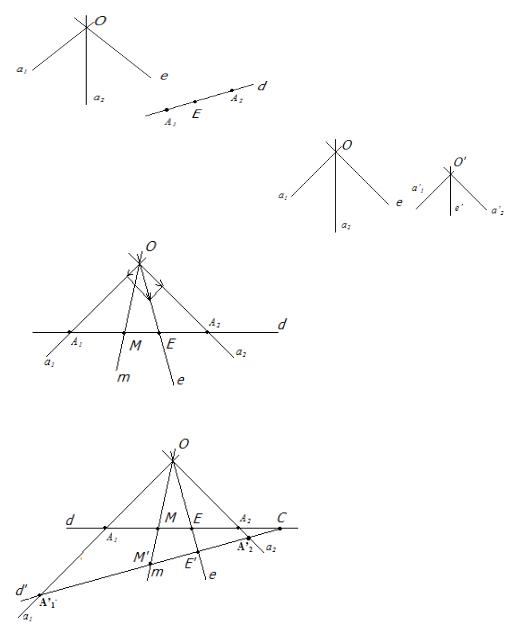
	Возьмем на плоскасці прамую d і пучок прамых
	Р(0) і зададзім у іх адпаведныя рэперы R і R’.
	Азначэнне: адвображанне прамой d на пучок
	Р(0) прамых :d (0) па закону: (xi ) d
	паставім у адпаведнасць прамую m (0), якая ў
	рэперы R’ мае тыя ж самыя каардынаты (хі), што і
		пункт М у рэперы
		R называецца
праектыўным адвображаннем		прамой d на пучок
Р(0).

Аналагічным чынам вызначаецца праектыўнае адвображанне

пучка на прамую і пучка на пучок.

Прыклад.

На праектыўнай плоскасці возьмем прамую d і пучок Р(0). Адвображанне f :d (0) па

14 закону: d, f (M) OM разглядалася напачатку курса праектыўнай геаметрыі. Яно называецца перспектыўным адвображаннем прамой d на пучок прамых Р(0). Паводле азначэння яно з’яўляецца праектыўным.

Возьмем цяпер две розныя прамыя d і d’ на пректыўнай плоскасці.

Разгледзім адвображанне f :d d', такое што адвольныя пункты М і М’=f(М) належаць прамой m пучка Р(0) для d . Яно называецца перспектыўным адвображаннем

прамой d на прамую d’. Пункт О называецца цэнтрам перспектывы. Кажуць, што пучок Р(0) праектуе прамую d на прамую d’. Не цяжка заўважыць, што перспектыўнае адвображане прамой на прамую з’яўляецца праектыўным. Сапраўды, у рэперах R=(A1;A2;E) на прамой d і R’=(A1’;A2’;E’) на прамой d’ адпаведныя пункты М і М’ маюць аднолькавыя праектыўныя каардынаты.

Такім чынам, перспектыўнае адвображанне з’яўляецца прыватным выпадкам праектыўнага. Заўважым, што тут агульны пункт C d d'прамых d і d’ адпавядае сам сабе.

Паўстае пытанне, у якім разе праектыўнае адвображанне прамой на другую будзе перспектыўным. Адказ дае тэарэма.

ТЭАРЭМА (прымета перспектыўнасці праектыўнага адвображання прамых): Праектыўнае адвображанне f адной прамой d на другую прамую d’ на праектыўнай

плоскасці з’яўляецца перспектыўным, тады і толькі тады, калі агульны пункт гэтых прамых C f (C) C'.

	БДПУ імя М.Танка	матэматычны факультэт				кафедра алгебры і геаметрыі
				Доказ:
			Неабходнасць: Дадзена, што праектыўнае
		адвображанне з’яўляецца перспектыўным. Тады С f (C)
		.	Дастатковасць: Дадзена f (C) C . Патрабуецца
		даказаць, што f – гэта перспектыўнае адвображанне.
			Возьмем на прамой d два розныя пункты А і В,
		адрозныя ад пункта С. Іх вобразамі пры праектыўным
	адвображанні f з’яўляюцца A' f (A),B' f (B), А’ і В’ – розныя, таму што f – гэта
	ўзаемаадназначнае адвображанне прамой d на прамую d’. Яно розныя пункты
	пераводзіць у розныя.
	Разгледзім цяпер перспектыўнае адвображанне g :d d' з цэнтрам перспектывы
	AA' BB'. Як і кожнае перспектыўнае адвображанне, яно праектыўнае і пераводзіць
	рэпер R=(A;В;С) прамой у рэпер R’=(A’;В’;С) гэтак як і дадзенае праектыўнае
	адвображанне f. Апрача гэтага пректыўнае адвображанне цалкам вызначаецца
	упарадкаванай парай адпаведных рэпераў. Значыць f супадае з g, а з гэтага вынікае, што f
		– перспектыўнае адвображанне.
				Няхай f – гэта ўзаемаадназначнае адвабражанне
		пучка Р(0) на пучок Р(0’). Прамая s называецца воссю
15		перспектывы дадзеных пучкоў. Заўважым, што дваіснай
		фігурай для пучка прамых з’яўляецца прамая, як
		мноства пунктаў.
				З дадзенай тэарэмы, поводле прынцыпа дваіснасці,
		вынікае тэарэма:
	ТЭАРЭМА (прымета перспектыўнасці праектыўнага адвображання пучкоў):
	Праектыўнае адвображанне		P(O) P(O') з’яўляецца перспектыўным тады і
	толькі тады, калі агульная прамаяf		ОО:	’ гэтых пучкоў адпавядае сабе г.зн. ОО’= =f(ОО’).
	ЗАДАЧА.
	Дадзены дзве розныя прамыя d і d’ праектыўнай плоскасці. Праектыўнае
	адвображанне f d d' зададзена адвольнымі рэперамі R=(A;В;С) і R’=(A’;В’;С’). Для
	адвольнага пункта М d	пабудуйце яго вобраз M' f (M).
			Аналіз. Заўважым, напачатку, што з трох пунктаў А,
		В,С не бальш як адзін можа супадаць са сваім вобразам,
		таму што згодна з умоваю прамыя d і d’ розныя. Будзем
		лічыць, напрыклад, што пункты А і А’- розныя.
		Правядзем прамую АА’ і возьмем на ей адвольныя два
		пункты О А і О' A'				у якасці цэнтраў двух пучкоў
		Р(О) і Р(О’) .Пазначым B0 OB O'B' ,
		C0 OC O'C', d0 B0C0 .
			Разгледзім два перспектыўныя адвображанні
					A A'		A0 A'
				g :d d0	B B'	, h:d0 d'	B0 B'
					C C'		C0 C'
	Складзем кампазіцыю гэтых адвображанняў

БДПУ імя М.Танка		матэматычны факультэт	кафедра алгебры і геаметрыі
	A A'
h g :d d'	B B'
	C C'

Як кампазіцыя двух перспектыўных, яно праектыўнае і вызначаецца рэперамі (А,В,С) і (А’,В’,С’). Значыць яно супадае з f. Такім чынам f h g . З гэтага вынікае пабудова

вобраза М’:

1) M0 OM d0 , 2)O'M0 , 3)M' M0O' d'. М’ – шукаемы вобраз пункта М. Заўважым, што ў гэтым разе мы праектыўнае адвображанне f прамой d на прамую d’

падалі ў выглядзе кампазіцыі двух перспектыўных. Але перспектыўныя адвображанні з’яўляюцца праектаваннямі адной прамой на другую. Значыць праектыўнае адвображанне адной прамой на другую атрымоўваецца ў выніку кампазіцыі двух пректаванняў. Адгэтуль вынікае назва – пректыўнае адвображанне і праектыўная геаметрыя.

§ 13. Складаны (падвойны) стасунак 4 пунктаў прамой.

На праектыўнай прамой зададзены праектыўны рэпер R=(A1;А2;Е) і дадзена ўпарадкаваная чацверка

розных між сабою пунктаў (А,В,С,D). Няхай у рэперы R А(х1,х2), В(у1,у2), С(z1,z2), D(u1,u2).

Азначэнне: Складаным або падвойным, ці інакш, гарманічным стасункам чатырох

16

x1x2

.

y1 y2

z1z2

u1u2

пунктаў А,В,С,D называецца лік (ABCD)

(1).

x1x2

.

y1 y2

1u2

z1z2

Каб азначэнне было карэктным дакажам

,uшто

складаны стасунак чатырох пунктаў не

залежыць ад выбару рэпера на прамой. А,В,С,D

1

2

1

2

1

2

Возьме новы рэпер R̃, адрозны ад R. Няхай у гэтым рэперы A(x̃,x̃), B(ỹ

,ỹ

), C(z̃,z̃),

D(ũ1,ũ2).

Карыстаемся формуламі пераўтварэння праектыўных каардынат на пректыўнай

i

i

j

прамой для пункта А. Старыя каардынаты выражаюцца праз новыя так x=cjx̃(i,j=1,2)

або ў разгорнутым выглядзе:

1

1~1

1 ~2

1

1

x

c1 x

c2 x

j

c1c2

0

2

2~1

, ∆ det

ci

2

2

2~2

x

c1

x

c2 x

c1 c2

Аналагічна будзе

1

1~1

1~2

z

c1 z

c2 z

2

2~1

2~2

z

c1

z

c2 z

1

x

2

1~1

1~2

2~1

2~2

~1

~2

1 2

~1~2

x

c1 x

c2 x

c1 x

c2 x

x x

.

c1c1

∆.

x x

.

z

1

z

2

1~1

1~2

2~1

2~2

~1

~2

1 2

~1~2

c1 z

c2 z

c1 z

c2 z

z

z

c2c2

z z

Аналагічныя выразы атрымаюцца і для астатніх вызначальнікаў з (1).

Падставіўшы гэтыя выразы ў правую частку роўнасці (1) атрымаем, што складаны

стасунак чатырох пунктаў не залежыць ад выбару праектыўнага рэпера на прамой.

Няхай

А,В,С калінеарныя пункты прамой зададзеныя ў дадзеным парадку

AC BC AC BC (2), R.

Азначэнне: Лік называецца простым стасункам трох калінеарных пунктаў.

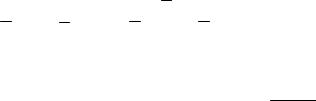
БДПУ імя М.Танка матэматычны факультэт кафедра алгебры і геаметрыі

Абазначаецца просты стасунак так (АВС)= .

У курсе аналітычнай геаметрыі мы разглядалі стасункі (адносіны) у якіх пункт дзеліць накіраваны адрэзак АВ .

АС СВ (3) АС ВС

Такім чынам просты стасунак (АВС) (4).

ТЭАРЭМА 1: Складаны стасунак чатырох пунктаў прамой выражаецца праз простыя

стасункі гэтых пунктаў формулай: (ABCD) (ABC) (5).

(ABD)

Доказ:

На

пашыранай прамой, як мадэлі праектыўнай возьмем праектыўны

рэпер

1 2

х

х2

R (A ,X

,E). Кожны ўласны пункт А мае пректыўныя каардынаты А(х ,х ) і

.

х1

1

Значыць А(1,х) і х – гэта афінная каардыната пункта А адносна афіннага рэпера з

пачаткам А1 і базісным вектарам

А1

. Аналагічна В(1,у), С (1,z), D(1,u). З роўнасці (1)

Е

1x

.

1y

1z

1u

(z x)(u y)

атрымаем (ABCD)

.

1x

.

1y

(u x)(z y)

1u

1z

17

Падлічым просты стасунак (АВС).

AC

BC z x (z y), BC 0 z y 0

(ABC)

z x

.

(ABD) u y .

z y

Аналагічным чынам можна атрымаць

u x

Адсюль

(ABC)

(z x)(u y)

(ABCD).

(ABD)

(z y)(u x)

Шпд.

Возьмем цяпер рэпер R=(A,B,C) на прамой, тады А(1,0), В(0,1), С(1,1), D(u1,u2)

10

.

01

11

u1u2

1

u

1

(ABCD)

( u

)

; (ABCD)

10

.

01

u2 ( 1)

u2

u1u2

11

Пункт D цалкам вызначаецца стасункам сваіх каардынат.

Такім чынам, калі на прамой дадзены тры пункты А, В, С, то кожны чацверты пункт D гэтай прамой, адрозны ад А, В, С адназначна вызначаецца складаным стасункам (ABCD).

З гэтага вынікае, што калі (ABCM)=(ABCN), то M=N.

Згодна з формуламі (1) можна атрымаць уласцівасці складанага стасунку:

1.Складаны стасунак захоўваецца, калі памяняць першую пару пунктаў з другой

(ABCD)=(CDАВ)

2.Калі ж памяняць месцамі пункты толькі адной пары, то складаны стасунак зменіць свае значэнне на адваротнае (BACD)=(ABCD)-1

(ABDC)=(ABCD)-1

Згэтых дзвюх уласцівасцей вынікае, што (ABCD)=(CDAB)=(BADC)=(DCBA).

Зпапярэдняга таксама вынікае, што (ABCD)=0 A=C або B=D

БДПУ імя М.Танка матэматычны факультэт кафедра алгебры і геаметрыі

(ABCD) 1 (ABC) 1 (ABC) (ABD) C D. (ABD)

ТЭАРЭМА 2: Кожнае праектыўнае пераўтварэнне плоскасці захоўвае складаны стасунак чатырох пунктаў прамой.

Доказ:

Няхай праектыўнае пераўтварэнне f пераводзіць пункты A,B,C,D адпаведна ў пункты A'B'C'D' d'. Яно вызначаецца ўпарадкаванай парай адпаведных рэпераў

R=(A,B,C) і R’=(A’,B’,C’). У рэперы R D(u1,u2). Гэтыя ж каардынаты мае пункт D’=f(D) у

	рэперы R’. На падставе папярэдняга (ABCD)	u1	; (A'B'C'D')	u1	. Адсюль
		u2		u2

(ABCD) (A'B'C'D').

Мае месца і адваротнае.

Такім чынам, складаны стасунак чатырох пунктаў прамой з’яўляецца інварыянтам групы праектыўных пераўтварэнняў. Гэта асноўны інварыянт праектыўнай групы.

Дваіснай фігурай да прамой, як мноства пунктаў будзе пучок прамых. А як жа тут вызначыць складаны стасунак чатырох прамых пучка?

Няхай a, b, c, d – чатыры розныя прамыя пучка Р(0) і прамая не праходзіць праз пункт О і перасякае гэтыя прамыя пучка адпаведна ў пунктах A, B, C, D.

18	ТЭАРЭМА 3: Складаны стасунак (ABCD) не залежыць ад выбару прамой .
	Доказ:
	Возьмем нейкую іншую прамую ', ўшто не праходзіць праз пункт О і абазначым
	пункты яе перасячэння з прамымі пучка A',B',C',D'.
	Цяпер разгледзім перспектыўнае адвображанне прамой на прамую 'з цэнтрам

перспектывы О. Яно, як і ўсялякае праектыўнае адвображанне захоўвае складаны стасунак чатырох пунктаў прамой. Таму (ABCD) (A'B'C'D').

Азначэнне: Складаным стасункам (abcd) чатырох прамых пучка называецца складаны стасунак (ABCD) чатырох адпаведных пунктаў прамой перспектыўнай дадзенаму пучку.

З папярэдняга паводле прынцыпа дваіснасці маем тэарэму 4 - ТЭАРЭМА 4: узаемнаадназначнае адвображанне аднаго пучка прамых на другі

з’яўляецца праектыўным тады і толькі тады, калі яно захоўвае складаны стасунак любой упарадкаванай чацверкі прамых.

§14. Поўны чатырохвяршыннік і яго гарманічныя ўласцівасці.

		B
A
	E
	В
G
M	F	N

Няхай А,В,С,D-чатыры пункты агульнага размяшчэння, гэта значыць, ніякія тры з якіх не належаць адной прамой.

БДПУ імя М.Танка

матэматычны факультэт

кафедра алгебры і геаметрыі

Азначэнне. Поўным чатырохвяршыннікам называецца фігура, утвораная чатырма пунктамі А,В,С,D агульнага размяшчэння (вяршыні) і шасцю прамымі (стораны), якія праходзяць праз іх.

Дзве стараны, якія не маюць агульнай вяршыні называюцца процілеглымі. Процілеглымі з’яўляюцца тры пары старон АВ і DС, АD і ВС, ВD і АС.

Пункты E ,F ,G перасячэння працілеглых старон называюцца дыяганальнымі пунктамі. Прамыя EF, GF, FG , якія праходзяць праз два дыяганальныя пункты, называюцца дыяганалямі поўнага чатырохвяршынніка.

Абазначым М, N-пункты перасячэння дыяганалі FG з працілеглымі сторанамі ВД і АС, якія праходзяць праз трэці дыяганальны пункт Е.

Дакажам, што складаны стасунак (GFMN)=-1

Разгледзім перспектыунае адвображанне f ׃ GF→AC з цэнтра перспектывы D. Пры гэтым адвображанні f(G)=C, f(M)=E, f(F)=A, f(N)=N. Перспектыўнае адвображанне з’яўляецца праектыўным і таму захоўвае складаны стасунак пунктау, таму

(GFMN)=(CAEN) (1)

Разгледзім цяпер перспектыўнае адвображанне φ ׃AC→GF з цэнтра перспектывы В. Пры гэтым адвображанні φ(С)=F, φ(A)=G, φ(N)=N, φ(E)=M. Адсюль складаны стасунак

(GFMH)=(FGMN)=1/(GFMN). Адсюль вынікае,што (GFMN)²=1. Заўважым,што М≠N,таму (GFM)≠(GFN)

З гэтага вынікае,што (GFMN)≠1. Значыць (GFMN)=-1

Азначэнне. Калі складаны стасунак (GFMN)=-1, чацвёрка пунктаў G, F, M, N называецца гарманічнай. Пункт N называецца чацвертым гарманічным да упарадкаванай тройкі пунктаў(G,F,M). У гэтым выпадку (GFNM)=-1. Значыць, пункт М таксама чацвёрты гарманічны да тройкі (G,F,N) пунктаў. Таму кажуць, што пункты M і N гарманічна

19 спалучаныя адносна пунктаў G,F. У такім разе (MNGF)=-1. Таму таксама гавораць, што пары (G,F) і (M,N) гарманічна падзяляюць адна другую. Абазначаюць гэта так M,N ~ G,F.

Усе дыяганальныя пункты раўнапраўныя, таму мы маем тэарэмы:

1)На кожнай дыяганалі поўнага чатырохвяршынніка існуе гарманічная чацвёрка пунктаў, якая складаецца з двух дыяганальных пунктаў і двух пунктаў перасячэння гэтай дыяганалі з парай процілеглых старон, што праходзяць праз трэці дыяганальны пункт.

2)На кожнай старане поўнага чатырохвяршынніка ёсць гарманічная чацвёрка пунктаў, якая складаецца з дзвюх вяршынь, дыяганальнага пункта і пункта перасячэння гэтай стараны з дыяганаллю, што праходзіць праз два іншыя дыяганальныя пункты.

3)Праз кожны дыяганальны пункт праходзіць гарманічная чацвёрка прамых, якая складаецца з дзвюх дыяганалей і дзвюх процілеглых старон.

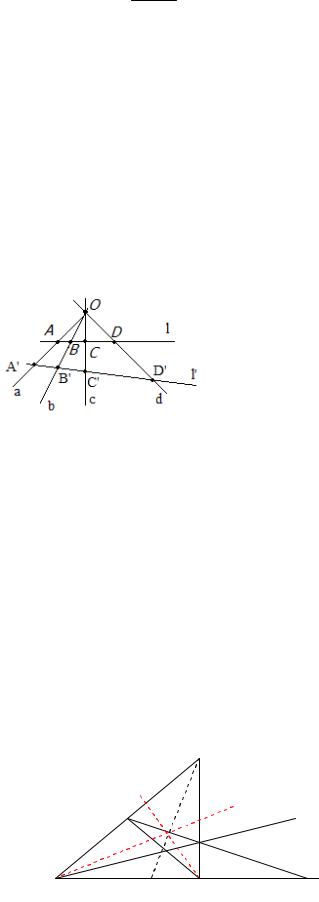
Задача.На прамой d дадзены тры пункты А,В,С. Пабудуйце чацвёрты гарманічны пункт D.

Заўвага. Першы пункт А заўсёды ў пары з другім пунктам В, а трэці пункт С у пары з шуканым пунктам D. Гэта задача цалкам праектыўная і таму яе можна рашыць з дапамогай толькі адной лінейкі.

Аналіз. Будзем лічычыць, што d – дыяганаль поўнага чатарохвяршынніка, А і В- дыяганальныя пункты, С-гэта пункт перасячэння гэтай дыяганалі са стараной , якая праходіць праз трэці дыяганальны пункт. Тады трэба знайсці пункт перасячэння прамой d

здругой стараной, якая праходзіць праз трэці дыяганальны пункт.

БДПУ імя М.Танка	матэматычны факультэт		кафедра алгебры і геаметрыі
	3
5	4	1
2
А		6
С	dВ	D
		§15. Інвалюцыя.

Азначэнне. Праектыўнае пераўтварэнне f прамой , якое само для сабе з’яўляецца

адваротным называецца інвалюцыяй.
f	f 1 =>	f 2 f f 1 E Значыць,	квадрат інвалюцыі ёсць тоеснае
пераўтварэнне прамой.

АB

	B'			A'
	Калі f(A)=A', то f(A')=A. Такім чынам, два адпаведныя пункты А і А' пераходзяць адзін у
20	другі незалежна ад парадку які пункт адлюстроўваецца ў які. Таму кажуць, што яны
	знаходзяцца ў падвойнай адпаведнасці і ўсялякія два пункты называюцца спалучанымі.
	Кожная пара спалучаных пунктаўгэта дзве пары адпаведных пунктаў, а
	праектыўнае пераўтварэнне вызначаецца трыма парамі (двумя праектыўнымі рэперамі)
	адпаведных пунктаў. Таму інвалюцыя цалкам вызначаецца дзвюма парамі спалучаных
	пунктаў.
	Тэарэма1. (Прызнак інвалюцыі)
	Калі	пры		праектыўным	пераўтварэнні прамой два яе пункты знаходзяцца ў
	падвойнай	адпаведнасці, то і кожныя два адпаведныя пункты таксама знаходзяцца ў
	подвойнай адпаведнасці.
	Заўвага. У такім разе праектыўнае пераўтварэнне ёсць інвалюцыя.
						Дадзена: f (A)=B і f(C)=D, f (B)=А
		А		В С	D
	Трэба даказаць, што f (D)=С

Доказ.

Няхай f (D)=D '. Дакажам, што D' =С

(АВСD) = (ВАDD'), (АВСD )= (ВАDС) =>(ВАDD´) = (ВАDС) => D´=С ш.п.д.

Могуць быць дзве магчымасці:

А В А' В'

1.

А,А´ В,В´ Пары падзяляюць адна другую. Няма падвойных пунктаў.

А

А´ B

B´

2.

А,А´ В,В´