2 курс 2 семестр

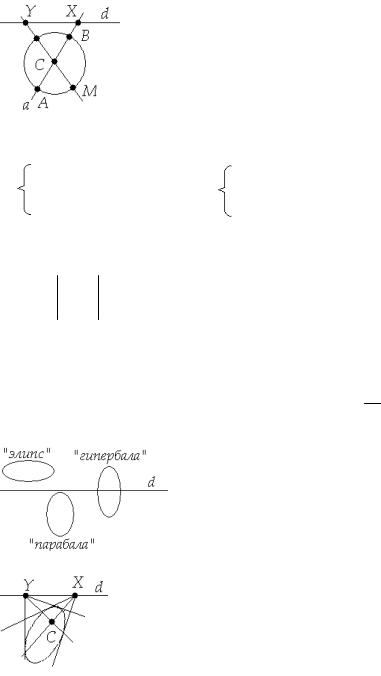
БДПУ імя М.Танка

матэматычны факультэт

кафедра алгебры і геаметрыі

Няхай прамая a праходзіць праз цэнтр С лініі Q другога парадку і перасякае яе ў пунктах А і В, X=AB∩d. Тады складаный стасунак (ABCX) = -1 для a, якая праходзіць праз пункт С.

Значыць С ёсць полюс прамой d.

Такім чынам “цэнтрам” лініі Q другога парадку на праектыўнай мадэлі пашыранай плоскасці можна назваць полюс “неўласнай”

прамой d.

Каардынаты цэнтра вызнычаюцца сістэмай ураўненняў:

2 jcj 0,		a21c1 a22c2 a23c3 0,
	cj 0,	або	a		c2 a		c3	0.
3 j		a c1		32		33
		31

Высвятлім, пры якой умове цэнтрам лініі другога парадку будзе “неўласны” пункт C(0; C2; C3). Гэта магчыма толькі тады, калі апошняя лінейная аднародная сістэма мае ненулявое рашэнне выгляду (0; C2; C3). А гэта мажліва толькі тады, калі

a22a23 0. a32a33

Такія лініі будзем называць лініямі парабалічнага тыпу.

Калі ж δ≠0, крывая Q мае цэнтрам “уласны” пункт. Такія лініі называюцца цэнтральнымі. Пры гэтым, калі ж δ>0, то з сістэмы раўнанняў ліній Q і прамой d x1=0

x3

можна атрымаць з квадратнага раўнання адносна , што лінія Q не мае неўласнай x2

прамой d агульных пунктаў. У гэтым лінія Q называецца крывой эліптычнага тыпу.

Калі ж δ<0, то лінія Q перасякае “неўласную” прамую d у 41 двух розных пунктах і называецца крывой гіпербалічнага тыпу.

На праектыўнай мадэлі пашыранай афіннай плоскасці “эліпсам”, “гіпербалай”, “парабалай” будзем называць авальную крывую другога парадку адпаведна эліптычнага, гіпербалічнага і парабалічнага тыпу.

Заўважым, што на самой праектыўнай плоскасці няма ніякай неўласнай прамой. Таму у праектыўнай геаметрыі няма ніякай розніцы паміж любымі дзвюма невыраджанымі лініямі другога парадку. Дыяметр лініі другога парадку дзеліць папалам паралельнымі між сабою хорды. Таму “дыяметрам” авальнай лініі другога парадку называецца паляра неўласнага пункта. Паводле прынцыпа ўзаемнасць кожный дыяметр парходзіць праз цэнтр лініі. З уласцівасцей пунктаў паляры

вынікае, ўто кожны з двух спалучанных дыяметраў дзеліць папалам хорды “паралельныя” другому дыяметру.

		§ 28 Праектыўная мадэль Эўклідавай плоскасці.
Возьмем	на	праектыўнай			плоскасці два камплексна-спалучанымі пункты
j (am	ibm ),	j	2	(am	ibm),
1
дзе am, bm R,		m N, i2=-1, (m=1,2,3), i – яўная адзінка.

Склаўшы раўнанні, можна пераканацца, што прамая j1 j2 сапраўдная і калі перайсці да новага рэпера, то пункты j1 і j2 застануцца таксама камплексна-спалучанымі.

За “неўласную” прамую d праектыўнай мадэлі пашыранай плоскасці возьмем прамую

j	j	2	г.зн. d= j j	2	.
1			1			j j , j		. Стаціянарная падгрупа
			Разгледзім		фігуру		2		Hj гэтай фігуры з’яўляецца
						1

падгрупай стацынаянарнай падгрупы Hd.

БДПУ імя М.Танка

матэматычны факультэт

кафедра алгебры і геаметрыі

Аналагічным чынам, як і раней у гэтым выпадку можна атрымаць у афінных каардынатах формулы пераўтварэння f Hj праектыўнай мадэлі афіннай плоскасці

A=P\d,

k(xcos ysin ) c1,

=±1

k(xsin ycos ) c2.

Але ж такі выгляд маюць формулы пераўтварэнняў групы Г падобнасці эўклідавай плоскасці. Значыць групы Hj і Г ізаморфныя.

Дзве прамыя a і b называюцца “перпендыкулярнымі” або “артаганальнымі”, калі адпаведная ім няўласныя пункты X, Y гарманічна падзяляюць пункты j1 і j2 г.зн. j1 , j2 ~X,Y.

“Акружнасцю” будзем называць кожную авальную лінію другога парадку, якая праходзіць праз пункты j1 і j2 . Гэтыя ўяўныя камплексна-спалучаныя пункты j1 , j2 , агульны для ўсіх

акружнасцей, называюцца цыклічнымі або кругавымі пунктамі праектыўнай мадэлі

пашыранай плоскасці A A d . Акружнасць не можа мець з прамой d агульгых сапраўдных пунктаў, значыць акружнасць – гэта прыватны выпадак эліпса.

Кожнае пераўтварэнне f Hj адлюстроўвае авльную крывую другога парадку у

42	авльную крывую, а	фігуру	j j , j	2	у яе	самую	і таму акружнасць пераходзіць у
			1
	акружнасць. Таму паняцце акружнасці з’яўляецца інварыянтным для кожнага
	пераўтварэння f Hj .
	Пераўтварэнне f	Hj мноства А так як і падобнасць с каэфіціентам К адлюстроўвае
	акружнасць радыўса	R у акружнасць радыўса KR.
	Разгледзем цяпер тыя		пераўтварэнні f			Hj	якія захоўваюць радыўс кожнай

акружнасці.

Відавочна, мноства ўсіх такіх пераўтварэнняў ўтварае некаторую групу D – парадку групы Hj .

Калі ж f D, то K=1. Формулы гэтага пераўтварэння маюць выгляд xcos ysin c1,

xsin ycos c2.

Яны супадаюць с формуламі руху эўклідавай плоскасці. Такім чынам група D iзаморфна групе рухаў эуклідавай плоскасці.

“Адлегласцю” АВ паміж пунктамі А і В называецца радыўс акружнасці з цэнтрам А і якая праходзіць праз пункт В.

Цыклічныя пункты j1 і j2 часам лічаць уяўнымі падвойнымі пунктамі некаторай эліптычнай інвалюцыі на прамой d. Заданне гэтых цыклічных пунктаў j1 і j2 можа быць вызначана з дапамогаю элептычнай інвалюціі з уяўнымі падвойнымі пунктаміj1 і j2 . Гэта інвалюцыя называецца абсалютнай. Прамая d разам з абсалютнай інвалюцыяй на ей называецца абсалютам плоскасці.

Тады дзве прамыя a і b “перпендыкулярныя”, калі яны перасякаюць прамую d у двух пунках, спалучаных у абсалютнай інвалюцыі.

Абсалютную інвалюцыю часам зручна задаваць Лагеравым пунктам. Гэта такі пункт, з якога кожная два спалучаныя пры абсалютнай інвалюцыі пункты на прамой d бачныя пад прамым вуглом.

БДПУ імя М.Танка

матэматычны факультэт

кафедра алгебры і геаметрыі

Прыклады.

X,Y ~ j1 , j2

а)

“Прамавугольнік” –

чатырохвугольнік у	якога	сумежныя	стораны	узаемна
	перпендыкулярныя.		Процілеглыя		–
	паралельныя.

б) “Ромб” – такі чатырохвугольнік у	якога
процілеглыя стораны паралельныя, а	дыяганалі
перпендыкулярныя.

в) “Квадрат”- гэта ромб у якога сумежныя стораны перпендыкулярныя.

43	г) “Акружнасць” – гэта авальная лінія		другога		парадку, у якой кожныя
	два спалучаныя	дыяметры узаемна перпендыкулярныя.		j	, j	2	~X,Y.
				1

Акружнасць вызначае на прамой d абсалютную інвалюцыю.

БДПУ імя М.Танка

матэматычны факультэт

кафедра алгебры і геаметрыі

Раздзел 2 МЕТАДЫ ПАБУДОВЫ ВІДАРЫСАЎ ФІГУР

				§1. Цэнтральнае праектаванне.
	Будзем лічыць, што			Эўклідава	прастора E3	дапоўнена няўласнымі элементамі.
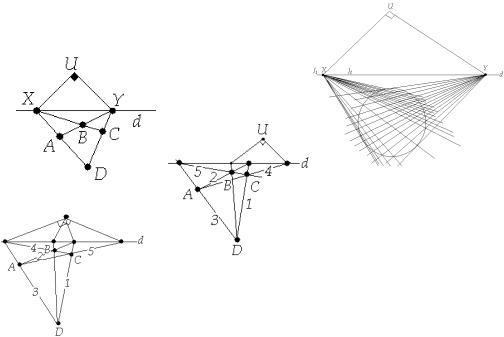
	Возьмем некаторую плоскасць , фігуру FI і пункт SI, прычым SI ,SI FI .
					Азначэнне Адвображанне			f1: F I
						па закону: f1 (M I ) M0 , дзе
						M0 S I M I	, M I		F I
						называецца праектаваннем
	FI					фігуры FI на плосасць					з
	SI					цэнтра SI .		называецца
	MI					Плоскасць
				F0		плоскасцю	праекцый або
				M0		плоскасцю відарыса.
		f1				Фігура FI называецца ары-
						гіналам. Фігура F f				I	)
44								0	1 (F
						называецца праекцыяй
						арыгіна ла FI на плоскасць
						.
	Плоскасць праекцый звычайна з’яўляецца плоскасцю аркуша паперы,								плоскасцю
	краснай дошкі. Можа здарыцца так, што праекцыя F фігуры FI не змяшчаецца на паперы
					0
	ці на дошцы. Тады плоскасць праекцый пераўтвараецца падобнасцю pтакой, каб фігура
	F p(F0 )мела	зручнае	размяшчэнне на плоскасці відарыса і памеры.						Фігура F
	называецца відарысам або выявай арыгінала.
	Заўважым, што калі няма неабходнасці ў выкарыстанні пераўтварэння падобнасці, то
	можна лічыць, што p E – гэта тоеснае пераўтварэнне. У такім разе відарысам арыгінала
	з’яўляецца яго праекцыя.				плоскасці I
	Разгледзім	праектаванне f1				на плоскасць		0I	з	цэнтра
	S I ,S I I ,S I 0I .
					f1: I 0I

S0	SI	f1		I		S	l
					f
		M	I		вонкавае	M	l0
					(знешняе)
							M0
	lI				0I	A
AI							J
					l0I
JI					M0I

БДПУ імя М.Танка

матэматычны факультэт

кафедра алгебры і геаметрыі

Яно з’яўляецца ўзаемнаадназначным адвображаннем плоскасці I

на плоскасць 0I і

кожную прамую

lI I

адлюстроўвае

на

прамую

l0I 0I

і

захоўвае

дачыненне

інцыдэнтнасці. Значыць праектаванне f1 з’яўляецца праектыўным адвображаннем.

Заўважым, што ўсе прамыя, якія злучаюць пары адпаведных пунктаў належаць адной і той

жа звязцы прамых з цэнтрам SI. Таму f1– гэта прыватны выпадак праектыўнага

адвображання плоскасці I

на плоскасць 0I . Яно называецца перспектыўным, а пункт SI

называецца цэнтрам

перспектывы

пласкасцей

I

і

0I .

Відавочна,

што

пункты

перасячэння

дзвюх адпаведных

прамых

lI і

l0I

належаць

прамой

JI= I 0I .

Яна

складаецца з падвойных пунктаў.

F I S I

, I , 0I на некаторую плоскасць

Далей праектуем гэту фігуру

з нейкага

пункта S0 прасторы, прычым S0 ,S0 F I .

Абазначым гэта праектаванне праз f:F I

.

Няхай S f (SI ),s f (sI ).

Разгледзім звужэнні гэтага адвображання на плоскасці I

і 0I .

fI I : I і fI I

: I

.

0

0

Гэта ёсць праектаванні пласкасцей

I

і 0I на плоскасць

з цэнтра

S0 . Паводле

45

папярэдняга яны з’яўляюцца праектыўнымі адвображаннямі.

Складзем

кампазіцыю

так,

каб

яна

пераводзіла

пункт

M

у

пункт

M0 ,(M M I

M0I M0 ) .

M ,

(fI 0I ) f1 (fI I )-1=h,

h(M)=M0,

h

– гэта праектыўнае

пераўтварэнне

плоскасці .

Кожны пункт А прамой J – падвойны пры пераўтварэнні h. Таму h – гэта гамалогія з

воссю J і цэнтрам S.

Плоскасць 0I

называецца асноўнай плоскасцю. Праектаванне f1: I

0I

называецца

ўнутраным праектаваннем,

а праектаванне ўсёй

фігуры

F I

S I , I , 0I

на плоскасць

відарыса называецца вонкавым або знешнім праектаваннем. Унутраная праекцыя

M0I

пункта M I называецца асновай пункта M .

Такім чынам, мы атрымалі тэарэму.

Вонкавае

праектаванне

f вызначае на плоскасці відарыса

гамалогію

h,

якая

адлюстроўвае праекцыю М кожнага пункта МI на праекцыю М0 яго асновы МI0.

Воссю гэтай гамалогіі h з’яўляецца праекцыя J прамой JI перасячэння пласкасцей I і

0I , а цэнтрам гамалогіі h – праекцыя S цэнтра SI унутранага праектавання.

Падобнасць захоўвае дачыненне інцыдэнтнасці пунктаў і прамых, таму гэта тэарэма

мае месца і для відарысаў.

Калі цэнтр SI праектавання f1

ёсць уласны пункт, то гэта праектаванне называецца

цэнтральным.

Калі ж

цэнтр SI –

гэта

няўласны пункт, то праектаванне

называецца

паралельным.

Відарысы, якія выкарыстоўваюцца ў сярэдняй школе павінны быць:

1)правільнымі (слушнымі): відарыс павінен быць падобным некаторай праекцыі арыгінала;

2)нагляднымі: ён павінен выклікаць прасторавае ўяўленне арыгінала;

3)вольна выкананымі: не павінны дастасойвацца ніякія пабудаванні, што не маюць дачынення да вывучаемай тэмы.

У школьнай практыцы ў асноўным выкарастоўваецца паралельнае праектаванне.

БДПУ імя М.Танка

матэматычны факультэт

кафедра алгебры і геаметрыі

§2. Паралельнае праектаванне і яго ўласцівасці.

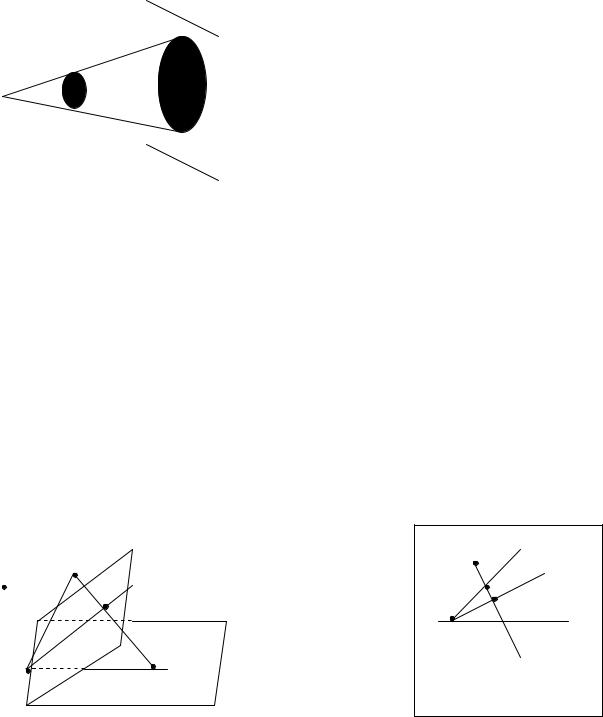
Напрамак паралельнага праектавання адназначна вызначаецца заданнем якойсці ўласнай прамой l.

Няхай фігура FI – гэта пэўная плоскасць , прычым I не паралельна 0I і прамая l

перасякае кожную з пласкасцей I і 0I .

Праектаванне f1 вызначае ўзаемнаадназначнае адвображанне f1: I 0I .

l

	I
	PI	0I
MI	mI
	NI
		PI
M	N	mI0

M I ,NI ,PI прамой mI ляжаць у адной праектавальнай плоскасці .

Праекцыяй прамой mI з’яўляецца лінія перасячэння праектавальнай плоскасці з плоскасцю праекцый 0I .

m0I 0I .

Такім чынам, калі mI не паралельна l, то праекцыяй прамой mI з’яўляецца прамая.

Захоўваецца інцыдэнтнасць пунктаў і прамой. Відавочна, просты стасунак

46

(M I NI PI ) (MNP).

Адсюль прыходзім да высновы, што

паралельнае праектаванне з’яўляецца

афінным

адвображаннем

Возьмем

прамую

mI I .

Усе

прамыя, якія

I праектуюць

пунктыI

плоскасці

на плоскасць

0 .

Тут усе прамыя, якія злучаюць адпаведныя пункты

(M I M),NI N,PI P , паралельныя паміж сабой і паралельныя прамой l. Таму паралельнае

праектаванне – гэта прыватны выпадак афіннага адвображання. Яно называецца

перспектыўна-афінным адвображаннем плоскасці I на плоскасць 0I .

Відавочна, што паралельныя прамыя, калі яны толькі не паралельныя праектавальным

прамым, праектуюцца ў паралельныя прамыя.

I

, 0I ,S I на плоскасць праекцый

Абазначым праз f праектаванне ўсёй фігуры F I

з цэнтра праектавання S0 ,

гэта

значыць f:F I

.

Гэта вонкавае праектаванне,

а

ўнутранае – f1.

Разгледзім выпадкі:

1) агульны выпадак: калі ўнутранае f1 і вонкавае f праектаванні паралельныя і лінія

перасячэння пласкасцей

J I I 0I уласная прамая. Цэнтры

SI

і S0

–

неўласныя

пункты гамалогіі.

Тады

на

плоскасці

відарыса

M

m

J f (J I

I

0I ) -

уласная

прамая,

а

J

цэнтр гамалогіі

–

неўласны пункт

M0

m0

(паралельныя

праектуюцца

ў

паралельныя).

БДПУ імя М.Танка	матэматычны факультэт	кафедра алгебры і геаметрыі
Гамалогія h на плоскасці відарыса з’яўляецца роднасным пераўтварэннем з воссю J і
напрамкам роднасці ММ0.
2) прыватны выпадак: калі I паралельна 0I ,		а f1 і f – паралельныя праектаванні.

Гамалогія h на плоскасці відарыса будзе з неўласнай воссю і неўласным цэнтрам.

Значыць, з’яўляецца паралельным пераносам. Ён вызначаецца вектарам MM0 .

3) унутранае праектаванне f1– цэнтральнае, а вонкавае f – паралельнае і I паралельна 0I .

				У гэтым выпадку гамалогія h мае
S	I			ўласны цэнтр S і неўласную вось s. Яна
		S		з’яўляецца гаматэтыяй з цэнтрам S.
MI	I			Знойдзем каэфіцыент k:
	NI	M	N	SM0	kSM M0S kMS k (M0MS).
	I	M0	N0
	0			Пры	паралельным	праектаванні
MI0	NI0
				(M0 MS) (M0I M I S I ) .
				Такім чынам k (M0I M I S I ).

§3. Відарысы плоскіх фігур з дапамогаю паралельнага праектавання.

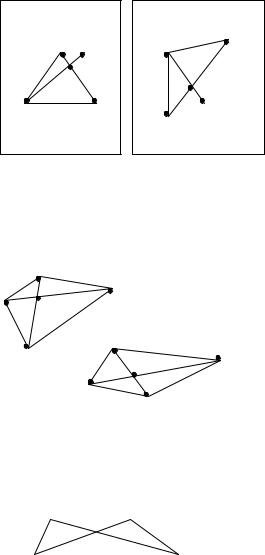
1) Пабудова відарыса трохвугольніка.

47

У плоскасці I

дадзены AI BICI –

I

арыгінал.

Праз

прамую

AI BI

правядзём плоскасць I

.

Няхай у

I

C

плоскасці

зададзены

адвольны

I

C

P

MNP. На

старане

AI BI

пабудуем

A

AI BIC падобны

дадзенаму

MNP.

BI

M

N

Праектаванне AI BICI

на плоскасць

у

напрамку

прамой

CI C атрымаем

праекцыю,

гэта

значыць

AI BICI

падобны адвольнаму дадзенаму MNP.

Значыць

відарысам

дадзенага

AI BICI

можа быць

любы наперад

зададзены

трохвугольнік MNP.

Прыклад. Роўнастаронні трохвугольнік можа мець відарысам адвольны рознастаронні трохвугольнік. Таму стасункі даўжынь непаралельных адрэзкаў могуць не захоўвацца. Але стасункі даўжынь паралельных адрэзкаў з’яўляюцца інварыянтнымі. Відарысам медыяны трохвугольніка з’яўляецца адпаведная медыяна відарыса.

OI AICI BI DI .

AI BI CI DI –

БДПУ імя М.Танка

матэматычны факультэт

Тэарэма. Няхай на плоскасці відарыса дадзены відарысы трох нейкіх пунктаў, якія не ляжаць на адной прамой і належаць некаторай плоскасці I , з дапамогай паралельнага праектавання не паралельнага I. Тады можна пабудаваць відарыс кожнага пункта плоскасці

I	АI	MI
	NI
BI		CI
Арыгінал

B	C
N	M
A
Відарыс

кафедра алгебры і геаметрыі

Доказ:

Возьмем

M I I ,NI AI CI BI M I

(AICI NI ) (ACN)

Відарыс N пункта NI вызначаецца адназначна. (BI NI M I ) (BNM). З гэтага знаходзім відарыс М пункта МI.

.

	2) Відарысы трохвугольнікаў.
48	CI		BI
	DI OI
	AI	C	B
		D	O A

Прыклад 1 Дадзена трапецыя пабудаваць яе відарыс.

DI CI

OI

AI BI

Правядзем дыяганалі чатырохвугольніка арыгінала. Няхай Паводле папярэдняга

відарысам AI BICI можа быць адвольныABC. Тады на падставе даказанай тэарэмы можна пабудаваць відарыс D вяршыні DI (спачатку пункт О, а пасля пункт D).

AI BI CI DI , дзе AI BI паралельна CI DI . Трэба

З падобнасці трохвугольнікаў можна атрымаць (дакажыце самастойна), што стасункі даўжынь асноў трапецыі захоўваюцца на відарысах.

Прыклад 2 Паралелаграм, уключаючы ромб, прамавугольнік і квадрат, могуць мець сваім відарысам адвольны паралелаграм.

Для пабудовы відарыса n-вугольніка дастаткова ведаць відарысы трох якіх-небудзь яго вяршынь. Астатнія вяршыні знаходзяцца пабудаваннем.

3) Відарыс акружнасці.

БДПУ імя М.Танка

матэматычны факультэт

кафедра алгебры і геаметрыі

У плоскасці I

дадзена акружнасць

– арыгінал. Калі пункт МI апіша

AI

dI CI I

акружнасць, то праектавальная прамая

I

M I M

апіша

кругавы

цыліндр.

M

OI

Плоскасць праекцый перасякае яго па

I

D

BI

лініі, якая ёсць эліпс. Такім чынам,

паралельнай

праекцыяй

акружнасці

з’яўляецца эліпс. Цэнтр акружнасці

A

d

C

праектуецца ў цэнтр эліпса. Падобнасць

p плоскасці праекцый пераводзіць эліпс

M

O

у эліпс і захоўвае просты стасунак трох

D

B

пунктаў.

Такім

чынам,

відарысам

акружнасці з’яўляецца эліпс, прычым

узаемнаперпендыкулярныя

дыяметры

акружнасці

выяўляюцца спалучанымі

Датычная dI у пункце

дыяметрамі эліпса.

AI да акружнасці выяўляецца прамой,

якая праходзіць праз

пункт А і паралельна дыяметру CD.

Разгледзім некаторыя спосабы пабудовы пунктаў эліпса, што з’яўляецца відарысам

акружнасці.

49

1) Дадзены спалучаныя дыяметры AB і CD эліпса.

d

С

Датычная

d

да

эліпса

ў

пункце

А

паралельна дыяметру СD, яе можна

A

B

пабудаваць. Мы маем задачу праектыўнай

геаметрыі

пабудовы

пунктаў

авальнай

D

лініі другога парадку, зададзенай чатырма

яе пунктамі і датычнай d у аднымI I з іх.

2) На адрэзку АВ як на даяметры пабудуем акружнасць і яе дыяметр C D .

CI

M I M //CI C

PI

MI

P

C

Разгледзім гамалогію з воссю АВ і

O

M

парамі адпаведных

пунктаў

(СIС) і

A

P1

B

неўласным

цэнтрам,

гэта

значыць

D

роднаснае

пераўтварэнне

плоскасці

з

воссю АВ. Для пункта МI акружнасці

D1

можна пабудаваць яго вобраз М, які

належыць эліпсу.

3) Пры роднасным пераўтварэнні захоўваецца паралельнасць прамых. Пункт P можна пабудаваць інакшPI PIICI C,P1PIIOC. Дастаткова пабудаваць чвэрць эліпса. Адлюстраваўшы сіметрычна адносна восей, атрымаем увесь эліпс.

Адрозніваюць два віды паралельнага праектавання:

1)артаганальнае паралельнае праектаванне, калі праектавальныя прамыя не перпендыкулярны плоскасці праекцый.

2)косавугольнае паралельнае праектаванне, дзе праектавальныя прамыя перпендыкулярны плоскасці праекцый .

БДПУ імя М.Танка

матэматычны факультэт

кафедра алгебры і геаметрыі

Заўважым, што артаганальнай праекцыяй акружнасці з’яўляецца акружнасць. Таму пры пабудове відарысаў акружнасці карыстаюцца часцей за ўсё артаганальным паралельным праектаваннем.

§4. Відарысы прасторавых фігур з дапамогаю паралельнага праектавання.

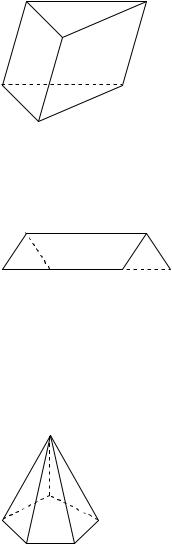
1) Відарыс прызмы.

Відарыс прызмы складаецца з двух роўных многавугольнікаў (відарысаў асноў), кожны з якіх атрымоўваецца з другога паралельным пераносам і паралелаграмаў – відарысаў бакавых граней. Відарысы асноў будуюцца як відарысы плоскіх многавугольнікаў.

Прыклад

Відарысам куба можа быць фігура, якая складаецца з шасці папарна-роўных паралелаграмаў.

50

2) Відарыс піраміды.

Складаецца з многавугольніка (відарыса асновы) і трохвугольнікаў з агульнай вяршыняй (відарысаў бакавых граней). Заўважым, што вышыня правільнай піраміды праходзіць праз цэнтр асновы. Заўважым, што для ўсечанай піраміды прамыя, якія змяшчаюць бакавыя канты, павінны перасякацца ў адным пункце. Таму спачатку зручней пабудаваць відарыс поўнай піраміды, а пасля гэтага відарыс усечанай піраміды.

3) Відарыс цыліндра.

У школьным курсе геаметрыі вывучаюцца толькі прамыя кругавыя цыліндры і конусы. Яны разглядаюцца не як паверхні, а як прасторавыя целы. Плоскасць праекцый лічыцца размешчанай вертыкальна, а вось цыліндра паралельная плоскасці і размешчана вертыкальна. Пры такім размяшчэнні і артаганальным праектаванні праекцыяй цыліндра з’яўляецца прамавугольнік. Відарыс правільны, але не наглядны. Таму часцей за ўсе карыстаюцца касавугольным праектаваннем.