2 курс 2 семестр

	БДПУ імя М.Танка		матэматычны факультэт		кафедра алгебры і геаметрыі
	прамая PS і палярай пункта S з’яўляецца прамая PR. Мы атрымалі, што ў
	трохвугольніку PRS кожная		старана	з’яўляецца палярай		працілеглай вяршыні. Ён
	называецца аўтапалярным.
	Такім чынам, калі поўны чатырохвяршыннік упісаны ў лінію Q другога парадку, то
	палярай кожнага яго дыяганальнага пункта з’яўляецца працілеглая яму дыяганаль.
	Адсюль вынікае спосаб пабудовы паляры вонкавага пункта Р адносна лініі Q
	другога парадку. Для гэтага ў дадзеную лінію ўпішам поўны чатырохвяршыннік так, каб
	дадзены пункт Р быў яго дыяганальным пунктам. Тады дыяганаль, якая праходзіць праз
	два іншыя дыяганальныя пункты R і S, з’яўляецца шукаемай палярай пункта P.
	Задача 2: Дадзены знешні пункт Р. Пабудуйце датычныя з пункта Р да лініі
		Q другога парадку.
	Спачатку пабудуем паляру р пункта Р. Няхай M1,M2 Q P. Тады M1P і M2P-
	гэта шукаемыя датычныя. Задача рашаецца толькі адной лінейкай.
	1 спосаб:			2 спосаб:
	М2					М2
		8
	7	1	Р	6	7	9
						3
31		2		5		2
	5	9		4		1	Р
	6				8	10
	3 М1	4			М1

§ 21. Пучок другога парадку. Лінія другога класа.

С

В

А

Пры перспектыўным

адвображанні

прамой l

на

'

'

'

'

l

прамую

l

прамыя

AA,BB

,CC

,..., якія

злучаюць

адпаведныя пункты, праходзяць праз адзін і той жа

пункт – цэнтр перспектывы О. Калі ж адвображанне

B’

l

'

прамой l на прамую l' толькі праектыўнае,

але не

перспектыўнае, то прамыя AA',BB',CC' не праходзяць

A’

С’

праз адзін пункт. Кажуць, што яны належаць аднаму

O

пучку другога парадку.

Пучок другога парадку з’яўляецца аднапараметрычным мноствам прамых. Сапраўды, становішча пункта А на прамой l вызначаецца з дапамогаю аднаго параметра – стасунку яго праектыўных каардынат. Праз кожны пункт прамой l праходзіць дакладна адна прамая пучка другога парадку.

Як вядома з матэматычнага аналізу, аднапараметрычнае мноства ліній мае абгортку, гэта значыць такую лінію, якая датыкаецца ўсіх ліній гэтага мноства.

БДПУ імя М.Танка	матэматычны факультэт			кафедра алгебры і геаметрыі
Азначэнне: Абгортка	прамых пучка другога парадку называецца лініяй
другога класа.
		O		l
	О’			l'

Каліж адвображанне прамой l на прамую l' не толькі праектыўнае, але і перспектыўнае, то пучок другога парадку распадаецца на два звычайныя пучкі Р(О) і Р(О’), дзе O' l l'. Крывая другога класа выраджаецца ў пару пунктаў О і О’.

Сфармулюем без доказу тэарэму Макларэна*: Мноства датычных да лініі другога парадку з’яўляецца пучком другога парадку.

Вынік: Усялякая лінія другога парадку з’яўляецца адначасова і лініяй другога класа і наадварот.

Гэта дазваляе абмежавацца вывучэннем толькі ліній другога парадку.

§ 22. Тэарэмы Паскаля і Брыаншона.

32	В		С	А	Е	С		a	b
	А			Д			f		c
							e
	F		Е	Д		F		d
		Q			В
							Тэарэма Брыаншона:
	Тэарэма Паскаля:						Азначэнне: Шасцістароннікам, апісаным
	Азначэнне: Шасцівяршыннікам, упісаным						вакол лініі другога класа называецца фігура,
	у лінію Q другога парадку, называецца						якая складаецца з упарадкаванай шасцёркі
	фігура, якая складаецца з упарадкаванай						прамых abcdef і шасці пунктаў перасячэння
	шасцёркі пунктаў ABCДEF гэтай лініі і шасці						гэтых прамых паслядоўна.
	прамых што злучаюць гэтыя пункты паслядоўна.						Дзве	вяршыні	шасцістаронніка
	Дзве стараны шасцівяршынніка называюцца						называюцца процілеглымі, калі пры абыходзе
	процілеглымі,			калі	пры	абыходзе	шасцістаронніка ў любым кірунку яны
	шасцівяршынніка ў любым кірунку яны						адасоблены адна ад другой дзвюма
	адасоблены адна ад другой дзвюма старанамі.						вяршынямі.

БДПУ імя М.Танка	матэматычны факультэт		кафедра алгебры і геаметрыі
Тэарэма Паскаля.			Тэарэма Брыаншона.
Е	С		F
			A
А	pasc
			Br	Е
D			B
	F
В
			D
Тры пункты перасячэння процілеглых			C
старон шасцівяршынніка, упісанага ў лінію
другога парадку належаць адной прамой		Тры прамыя, якія злучаюць процілеглыя
(прамой Паскаля).		вяршыні шасцістаронніка, апісанага вакол
Доказам тэарэмы Паскаля будзе першая		лініі другога класа праходзяць праз адзін
частка доказу тэарэмы 2 Штайнера.		пункт (пункт Брыаншона).
		Тэарэма Брыаншона з’яўляецца дваіснай
		для тэарэмы Паскаля і таму мае месца на
		падставе прынцыпа дваіснасці.

Выконваюцца і тэарэмы, адваротныя тэарэмам Паскаля і Брыаншона.

33		§ 23. Прыватныя выпадкі тэарэм Паскаля і Брыаншона.
	Тэарэмы Паскаля і Брыаншона могуць быць прыстасаванымі і да фігур з меншай
	колькасцю вяршынь ці старон. Калі пункт В імкнецца да пункта А, то
	В	сякучая імкнецца заняць становішча датычнай. У такім разе будзем
		лічыць, што некаторыя суседнія вяршыні або стораны супадаюць. Пры

Агэтым старана шасцівяршынніка ператвараецца ў датычную, а вяршыня шасцістаронніка – у пункт дотыку.

Тэарэма 1:

pasc

У кожным пяцівяршынніку, упісаным у

лінію Q другога парадку, пункты

перасячэння дзвюх пар несумежных яго

старон і пункт перасячэння апошняй пятай

стараны з датычнай у процілеглай ёй

вяршыні належаць адной прамой (прамой

Паскаля).

Тэарэма 1*:

Br

Калі вакол лініі другога класа апісаны пяцістароннік, то прамыя, якія злучаюць дзве пары несумежных вяршынь яго і прамая, што злучае апошнюю пятую вяршыню з пунктам дотыку процілеглай ёй стараны, перасякаюцца ў адным пункце (пункце Брыаншона).

БДПУ імя М.Танка	матэматычны факультэт	кафедра алгебры і геаметрыі
Тэарэма 2:	Тэарэма 2*:

	Br
pasc
	Калі вакол лініі другога класа апісаны
Калі ў лінію другога парадку ўпісаны	чатырохстароннік, то чатыры прамыя, якія
чатырохвяршыннік, то дзве пары	злучаюць папарна процілеглыя вяршыні, а
процілеглых яго старон і дзве пары датычных	таксама пункты дотыку процілеглых старон,
у процілеглых яго вяршынях перасякаюцца	праходзяць праз адзін пункт (пункт
папарна ў чатырох пунктах, якія належаць	Брыаншона).
адной прамой (прамой Паскаля).
Тэарэма 3:	Тэарэма 3*:

	34	Br
		Прамыя, якія злучаюць вяршыні
	Тры пункты перасячэння старон	трохстаронніка, апісанага вакол лініі другога
	трохвяршынніка, упісанага ў лінію другога	класа, з пунктамі дотыку процілеглых ім
	парадку, з датычнымі ў процілеглых ім	старон, праходзяць праз адзін пункт (пункт
	вяршынях належаць адной прамой (прамой	Брыаншона).
	Паскаля).

§ 24. Праектыўная класіфікацыя ліній другога парадку.

Няхай на праектыўнай плоскасці ў рэперы R (A1A2A3E) лінія Q другога парадку

зададзена раўнаннем ( ) 0,або a xixj 0 (i,j=1,2,3). (1) Як вядома

(з першага

ij

курса) квадратычная форма ( ) a xixj,

дзе a

ij

R з дапамогай лінейнага

ij

невыраджанага пераўтварэння зменных xi

cij j ,

det

cij

0,

cij R (2)

(3).

можа быць прыведзена да кананічнага выгляду

b

( 1)2

b ( 2 )2

b

( 3)2

11

22

33

Пры гэтым ранг квадратычнай формы не змяняецца, а індэкс квадратычнай формы не залежыць ад спосабу прывядзення формы да кананічнага выгляду.

x1 c11 1 c21 2 c31 3,
	2	2	1	2			2	2	3		,
Формулы (2) x		c1		c2				c3
	3	3	1	3		2		3	3	.
x		c1 c2						c3

БДПУ імя М.Танка

матэматычны факультэт

кафедра алгебры і геаметрыі

з’яўляюцца формуламі пераўтварэння праектыўных каардынат на праектыўнай

плоскасці. Таму існуе новая сістэма каардынат (A'

A'

A' E'

) R' , дзе A'

(C1;C2

;C3),

1

2

3

1

1

1

1

A'

(C1

;C

2;C3),

A'

(C1;C2;C3), адносна якой раўнанне лініі Q мае кананічны выгляд

2

2

2

2

3

3

3

3

b ( 1)2

b ( 2 )2

b

( 3)2 (4).

11

22

33

(4).

Высветлім геаметрычны сэнс новага рэпера, у якім лінія Q мае кананічны выгляд

Раўнанне паляры пункта A(a1;a2;a3) адносна крывой Q, якая зададзена раўнаннем

(1) мае выгляд

a ajxi 0.

ij

Для лініі, зададзенай раўнаннем (4) яно будзе b a1 1

b

a2 2 b

a3 3

0.

(5)

11

22

33

Каардынатныя пункты A'

у рэперы R' (A';A' ;A' ;E'

) маюць каардынаты A'

(1;0;0),

i

1

2

3

1

A'

(0;1;0),

A' (0;0;1). Калі A A , то каардынаты пунктаў A'

(i j)

2

3

i

j

задавальняюць раўнанню (5) паляры і таму гэтыя пункты A'j

належаць паляры пункта

A' . Такім чынам, кожная старана каардынатнага трохвяршынніка

з’яўляецца

i

A3'

палярай трэцяй процілеглай ёй вяршыні. Гэты

трохвяршыннік называецца аўтапалярным I роду.

Мы прыйшлі да высновы, што прывядзенне раўнання лініі

A'

A'

1

2

35

другога парадку да кананічнага выгляду ёсць пераход да такога праектыўнага рэпера

R' (A';A' ;A' ;E') , у якога каардынатны трохвяршыннік

A' A'

A'

з’яўляецца аўтапалярным

I роду.

1

2

3

1

2

3

Даследуем кананічнае раўнанне (4). Магчымы 3 выпадкі:

I. b11 0,

b22 0,

b33

0, гэта значыць ранг матрыцы

aij

роўны 3.

1). усе каэфіцыенты bii

аднаго знака. Можна лічыць, што ўсе каэфіцыенты дадатныя.

Пяройдзем да новай сістэмы каардынат па формулах

i

2 b ( i )2. У гэтым рэперы

раўнанне лініі Q будзе (x1)2 (x2)2 (x3)2 0.

(1) Яно(xвызначае) ii

Ø. Лінію Q называюць

нулявой крывой.

2). каэфіцыенты bii розных знакаў.

Няхай b11 0,

b22

0,

b33 0. Перойдзем да новай сістэмы каардынат па формулах

xi

i . Атрымаем раўнанне (x2)2 (x3)2

b

(x1)2

0 (2). Лінія Q называецца

ii

авальнай крывой другога парадку.

II. У раўнанні (4) адзін каэфіцыент роўны нулю. Таму ранг матрыцы

aij

роўны 2.

Няхай, напрыклад сярэдні каэфіцыент b22 0,

b11 0, b33

0.

1).b11

і b33

аднаго знака. Можна лічыць іх дадатнымі. Перайшоўшы да новай сістэмы

каардынат па формулах x1

1, x2 2,

x3

3 атрымаем раўнанне

b

b

11

33

(x1)2 (x3)2

0. (3)

Яму задавальняюць тройкі каардынат (0;x2;0). Яны вызначаюць адзін

пункт на праектыўнай плоскасці.

2). b11

і b33

розных знакаў. Няхай b11 0,

b33 0. Аналагічным чынам, як у

папярэднім выпадку прыйдзем да раўнання (x1)2 (x3)2 0

x1 x3

0

(4).

1

3

0

x x

Лінія Q ёсць аб’яднанне дзвюх прамых. Кажуць, што яна распадаецца на пару прамых. III. У раўнанні (4) два каэфіцыенты роўныя нулю, гэта значыць ранг матрыцы aij

роўны адзінцы.

БДПУ імя М.Танка	матэматычны факультэт			кафедра алгебры і геаметрыі
Няхай, напрыклад b	b	0, b	0. Раўнанне (4) мае выгляд (x3)2 0. Лінія Q
11	22	33

другога парадку ёсць пара супаўшых прамых. Мы прыйшлі да высновы: на праектыўнай плоскасці існуе пяць тыпаў ліній другога парадку:

1). (x1)2 (x2)2 (x3)2 0- нулявая крывая 2). (x2)2 (x3)2 (x1)2 0- авальная крывая

3). (x1)2 (x3)2 0- пункт

4). (x1)2 (x3)2 0- пара розных прамых

5). (x3)2 0- пара супаўшых прамых

Заўважым, што мы правялі класіфікацыю ліній другога парадку на праектыўнай плоскасці па рангу і індэксу квадратычнай формы ( ) aijxixj, якія не змяняюцца пры

любых праектыўных пераўтварэннях. Таму гэтыя тыпы крывых праектыўна розныя. Гэта значыць, што не існуе праектыўнага пераўтварэння плоскасці, якое адлюстроўвае крывую аднаго тыпу ў крывую другога тыпу. Для нулявой і авальнай крывой ранг матрыцы aij

роўны 3, таму гэтыя крывыя не выраджаныя. Крывыя (3) і (4) маюць па аднаму асабліваму пункту, а для крывой (5) кожны пункт асаблівы.

36	§ 25. Канструктыўныя тэарэмы Штайнера, тэорыі авльных ліній другога
	парадку.
	На праектыўнай плоскасці дадзены два пучкі прамых Р(О) і Р(О') з рознымі цэнтрамі
	О і О' і вызначана праектыўнае адвображанне f: Р(О) → Р(О').

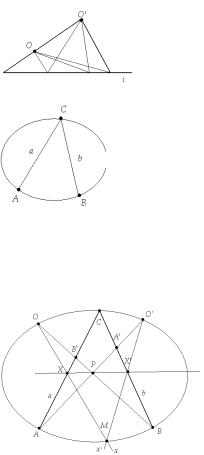
Тэарэма 1.

Мноства ўсіх пунктаў перасячэння адпаведных прамых двух праектыўных пучкоў ёсць лінія Q другога парадку, якая праходзіць праз цэнтры О і О' пучкоў.

Доказ Увядзем на плоскасці праектыўную сістэму каардынат

R=(A1A2A3E). Праектыўнае адвображанне f: (О) → Р(О') вызначае некаторае праектыўнае пераўтварэнне ў плоскасці (адлюстроўвае прамую на прамую). Яно вызначаецца формуламі:

yi cij xj ,

det

cij

0

(1)

Яно пераўтварае рэпер R у новы рэпер R=(A′1A′2A′3E′). Возьмем цяпер прамую X Р(О). У рэперы R яна вызначаецца аднародным раўнаннем I ступені:

a x1	a	2	x2	a	x3 0		(2)
1				3
прычым a				2 a	2	a2 0.
			1		2	3
Яе вобраз X'=g(x') у новым рэнеры R' мае тое ж самае раўнанне ai							yi 0 .
У дадзеным першапачатковым рэперы R раўнанне прамой X' будзе
a сi	xj 0						(3)
i j

Каардынаты пунктаў X перасячэнне X ∩ X' задавальняюць сістэме раўнанняў (2) – (3).

Адзначым, што прынамсі адна з каардынат x1, x2, x3 адрозніваецца ад нуля . Няхай, напрыклад x1≠0. Знайшоўшы з (2) a1 і падставіўшы яго выраз у (3) атрымаем аднароднае раўнанне другой ступені адносна

БДПУ імя М.Танка

матэматычны факультэт

кафедра алгебры і геаметрыі

каардынат x1, x2, x3, якое і вызначае лінію Q другога парадку. Разгледзім агульную прамую ОО' = b пучкоў, лічачы што, адпавядае прмая b′ = f (b) P(О') О' = b∩ b′ => О' Q.

Аналагічным чынам можна даказаць, што О Q.

Значыць цэнтры O і О' ўтваральных праектыўных пучкоў належаць лініі другога парадку.

Прамая b′ мае два супаўшыя пункты перасячэння з лініяй Q і таму з’яўляецца датычнай ў пункце О'.

Гэта тэарэма дазваляе вызначыць лінію другога парадку з дапамогаю праектыўнага адвображання аднаго пучка прамых P(О) на другі пучок P(О').

Заўвага Каліж праектыўнае адвображанне з’яўляецца перспектыўным, то

лініях другога парадку у пару розных прамых, з якіх адна – гэта вось спектывы пучкоу, а другая - гэта агульная прамая пучкоў.

Можна даказаць, што цэнтры O і О' можна выбіраць на лініі Q адвольна.

	Тэарэма 2. (асноуная тэарэма адвольная да тэарэмы 1).
	Усе пункты адвольнай лініі Q другога парадку праектуюцца з
37	адвольных двух яе пунктаў двума праектыўнымі пучкамі.
	Інакш кажучы, калі два пункты А і В належаць адвольнай лініі Q
	другога парадку і кожнай прамой a пучка P(A) паставіць у адпаведнасць прамую b пучка
	P(B), якая перасякае прамую a у пункце C Q, то атрыманае, адвображанне пучка P(A) на
	пучок P(B) з’яўляецца праектыўным.

Доказ

Няхай лінія Q атрымана у выніку праектыунага адвображання f: Р(О) → Р(О').

Возьмем два адвольныя пункты A Q і B Q. Дакажам, што можна вызначыць праектыўнае адвображанне пучка P(A) на пучок P(B) у выніку якога атрымаем туюж самую

лінію Q другога парадку.

Абазначым C = a ∩ b, X = x ∩ a, X′ = x′ ∩ b′.

Зафіксуем пункт С, а пункт М няхай прабягае крывую

Q.Тады прамыя xі x′ апішуць пучкі Р(О) і Р(О') адпаведна,

апункты X і X′ апішуць на не рухомых прамых a і b два прамалінейныя шэрагі пунктаў. Дакажам, што яны не толькі праяктыўныя, але і перспектыўныя.

Дзеля гэтага разгледзім перспектыўныя адвображанні g: a → P(O) і h: P(O') → b.

Паводле умовы дадзенае адвображанне f: P(O) → P(O') праектыўнае.

Кампазіцыя hofog ставіць у адпаведнасць пункту X а, пункт X′ b. Як кампазіцыя

праектыўных адвображанняў яна з’яўляецца праектыўнай. Дакажам, што гэта кампазіція ёсць перспектыўнае адвображанне. Для гэтага трэба даказаць, што агульны пункт С прамых a і b сам сабе адпавядае, гэта знпчыць, што ён ёсць падвойны пункт.

Калі пункт М супадзе з пунктам С, то пункты Х і X′ адначасова супадуць з пунктам С. А гэта азначае, што агульны пункт С = a ∩ b сам сабе адпавядае. Адсюль вынікае што, hofog – перспектыўнае адвображанне.

Пабудуем цэнтр перспектывы Р прамых a і b. P AA', P BB' => P = (AA') ∩ (BB'). Пункты Х і Х' адпаведныя пры перспектыўным адвображанні hofog: a→ b. Таму тры

пункты Х, Х', Р належаць адной прамой. Яна з’яўляецца прамой Паскаля.

Заўважым, што тут мы маем 6-вяршыннік упісаны ў лінію II парадку, а X, X', P – гэта пункты перасячэння процілеглых старон. Такім чынам мы даказалі тэарэму Паскаля.

	БДПУ імя М.Танка	матэматычны факультэт		кафедра алгебры і геаметрыі
	Зафіксуем цяпер пункт М, а пункт С няхай прабягае лінію Q. Прамыя a і b будуць
	апісваць 2 пучкі Р(А) і Р(В). Пункты Х і Х' будуць апісваць на нерухомых прамых x і x'
	два прамалінейныя шэрагі пунктаў.
	Разгледзем перспектыўныя адвображанні P1: P(A) → x, hofog: x→x', P2: x'→P(B).
	Кампразіцыя Р2 hofog Р1 кожнай прамой a Р(A) ставіць у адпаведнасць прамую				b
	Р(В). Гэта ёсць кампазіцыя перспектыўных адвображанняў і таму з’яўляецца
	праектыўным. Гэта і патрэбна было даказаць.
	Вынікі з тэарэм Штайнера.
	Вынік 1. Калі на праектыўнай плоскасці зададзены 5 пунктаў, ніякія тры з якіх не
	належаць адной прамой, то існуе дадзеная лінія Q другога парадку, што праходзіць праз
	кожны з гэтых пунктаў.
		Доказ.
		Дадзены на плоскасці 5 пунктаў агульнага размяшчэння А, В,
		С, D, Е. Возьмем, напрыклад, два першыя пункты А і В у якасці
		цэнтраў двух пучкоў і вызначым праектыўнае адвображанне φ так
		φ: P(A) → P(B)	AC→ BC
			AD→ BD
38			AE→ BE.
	Яно не перспектыўнае, таму што тры пункты С, D, Е не належаць адной прамой.
	Паводле тэарэмы 1 мноства ўсіх пунктаў перасячэнне адпаведных прамых пучкоў Р(А) і
	Р(В) з’яўляецца некаторай лініяй Q другога парадку, якая праходзіць праз усе дадзеныя
	пункты А, В, С, D, Е.
	Можна даказаць адзінасць гэтай крывой метадам ад процілеглага.
	Вынік 2. Калі на праектыўнай плоскасці дадзены чатыры пункты А, В, С, D ніякія тры
	з каторых не належаць адной прамой і праз пункт А праходзіць прамая
	а, якой не належыць ніводны з пунктаў В, С, D, то існуе адзіная лінія Q
	другога парадку, якая праходзіць праз дадзеныя пункты А, В, С, D				і

якая прамую а мае сваёй датычнай у пункце А.

Вынік 3. Няхай на праектыўнай плоскасці дадзены тры пункты А, В, С, якія не належаць адной прамой і прамыя a, b адпаведна праходзіць праз пункты А і В і не змяшчаюць адпаведна пунктаў В, С і А, С. Тады існуе адзіная лінія Q другога парадку, якая праходзіць праз пункты А, В, С і мае прамыя а і b сваімі датычнымі ў пунктах А і В.

Задача.

Адной лінейкай пабудуйце датычную да дадзенай акружнасці ў дадзеным яе пункце А.

Аналіз.

Упішам у дадзеную акружнасць пяцівяршыннік, каб адно з яго вяршынь быў дадзены пункт А. Пабудуем прамую Паскаля і знаходзім пункт перасячэння процілеглай пункту А стараны з прамой Паскаля. Злучыўшы яго з дадзеным пунктам А, знойдзем шукаемую датычную да акружнасці у пункце А.

БДПУ імя М.Танка

матэматычны факультэт

кафедра алгебры і геаметрыі

§ 26 Геаметрыя на праектыўнай плоскасці з фіксаванай прамой

Возьмем на праектыўнай плоскасці якую-небудзь прамую d і разгледзем мноства Hd усіх праектыўных ператварэнняў плоскасці, якія адлбстроўваюць прамую d на сябе.

Відавочна, што мноства Hd з’яўляецца падгрупай праектыўнай группы. Будзем называць яе стацыянарнай падгрупай прамой d.

Знойдзем формулы, якія вызначаюць пераўтварэнне f Hd у спецыяльна выбранным праектыўным рэперы R = (A1A2A3E) калі

A2A3 d.

A2(0; 1; 0), A3(0;0;1)

x1 x2 x3

Раўнанне прамой d = A2A3 будзе 0 1 0 0 x1 0. 0 0 1

Няхай пераўтварэнне f Hd пункт М(x1; x2; x3) пераводзіць у пункт М' (y1;y2; y3). Яно прамую d адлюстроўвае на сябе. Таму у выбранным рэперы R раўнанне прамой d будзе y1

= 0.

Запішам формулы праектыўнага пераўтварэнне плоскасці пры λ=1.

	yi cij xj (1)						det		cij		0				i, j 1,2,3
39	Калі x1=0, то для x2,x3							павінна быць y1 = 0. Таму формулы (1) маюць выгляд:
	1 c1x1,
	1
	2 c2x1 c2x2				c2x3, (2)						с1	с1				0
	1			2		3					2			3
	3 c3x1 c3x1 c3x3,
	f Hd будзе			M d		=> M f (M) f (d) d .
	1			2		3
	Тут det	ci		c1	c2c2		0, => c1				0			і	c2c2			0.
					2	3										2	3
		j		1	c3c3					1					c3c3
					2	3										2	3
	Кожнае праектыўнае пераўтварэнне захоўвае дачыненне прыналежнасці. Таму, для
	Hd можна разглядаць у якасці группы пераўтварэння мноства A=P2\d усіх пунктаў
	праектыўнай плоскасці, якія не належаць прамой d. Калі M(x1;x2;x3) A, то x1 ≠0 і для
	яго вобраза M							1	;y	2	;y	3	)	y	1	≠0.
				f (M) M (y
	Для пунктаў мноства А формулы (2)																пераўтварэння f Hd можна запісаць інакш,

падзяліўшы другую і трэцюю рознасці пачленна на першую.

	y2				c2				c2 x2										c2 x3
					1				2										3
	y	1			1				1			x		1					1			x		1
					c				c										c
			1					1									1							(3)
	y3				c3			c3 x2
																		c3 x3
				1				2										3
	y	1		1				1				x	1					1				x	1
					c				c									c
			1					1									1
Зўважым,									што										калі дадзеный рэпер R выгляду R=(A1,X0,Y0,E), то стасунак

y2 y3

праектыўных каардынат з’яўляецца адпаведнымі афіннымі каардынатамі y1 x , y1 y ,

	x3	x,	x3	y .
	x1		x1

Абазначаўшы свабодныя члены праз x0, y0, а каэфіціенты праз a11, a12, a21, a22, з сістэмы (3) атрымаем

x a11x a12 y x0,	прычым	a11a12	0
y a21x a22 y y0.		a21a22

БДПУ імя М.Танка

матэматычны факультэт

кафедра алгебры і геаметрыі

Мы атрымалі формулы афінных пераўтварэнняў афіннай плоскасці, г.зн. такіх якія прамую пераводзяць у прамую.

Такім чынам, група Hd ізаморфна групе афінных пераўтварэнняў плоскасці.

Можна пераканацца, што для мноства A=P2\d выконваюцца ўсе аксіёмы Вейля і гэтае мноства А – гэта праектыўная мадэль афіннай плоскасці.

Каб ад гэтай мадэлі А перайсці да праектыўнай мадэлі A пашыранай плоскасці неабходна да мноства А далучыць выключную прамую d.

Такім чынам прамая d выконвае ролю неўласнай прамой у праектыўнай мадэлі пашыранай плоскасці. Таму, натуральна, гэту прамую d назваць “неўласнай” прамой у

праектыўнай мадэлі пашыранай прлоскасці A .

Прыклады.

“Паралельнымі” у праектыўнай мадэлі пашыранай плоскасці называюцца такія дзве прамыя а і b, адрозныя ад прамой d, якія перасякаюцца ва “неўласным” пункце, г.зн. у пункце на прамой d.

40

“ Простым стасункам” (ABC) трох калінеарных пунктаў АВС называюцца складаны

стасунак чатырох пунктаў (ABCX), дзе X=AB∩d.

Такім чынам:

(ABC)=(ABCX)

Паралельнасць прамых і просты стасунак трох пунктаў з’яўляюцца інварыянтамі

групы Hd праектыўных пераўтварэнняў.

З дапамогай простага стасунка трох пунктаў можна вызначыць як звычайна паняцці

“ляжаць паміж”, “адрэзак”, “прамень” і г.д.

Прыклад.

Пункт С называецца “сярэдзінай” адрэзка АВ, калі (ABCX) = -1 г.зн. C,X ~ A,B, дзе

X=AB∩d.

§ 27 Лініі другога парадку на праектыўнай мадэлі афіннай і пашыранай

плоскасці.

Возьмем на праектыўнай плоскасці лініі другога парадку Q, зададзенную раунаннем

a xi xj 0, або ў разгорнутым выглядзе:

ij

a (x1)2 a

22

(x2 )2

a

33

(x3 )3 2a

12

x1x2

2a x1x3

2a

23

x2 x3 0.

11

13

Разгледзем цяпер Q΄ пунктаў лініі Q, якія належаць праектыўнай мадэлі А афіннай плоскасці, г.зн. Q΄=Q∩A. Таму x1≠0. Можна лічыць, што x1=0. Раўнанне мноства Q΄ будзе

a22 (x2 )2 a33 (x3 )2 2a23 x2 x3 2a12 x2 2a13 x3 a11 0.

Мы атрымалі агульнае раўнанне лініі другога парадку на афіннай плоскасці. Возьмем цяпер лінію Q другога парадку на праектыўнай мадэлі пашыранай плоскасці

A A d .

Высветлім, як можна даць азначэнне цэнтра лініі другога парадку. Цэнтр дзеліць папалам кожную хорду, якая прахлдзіць праз яго.