введение в тфп

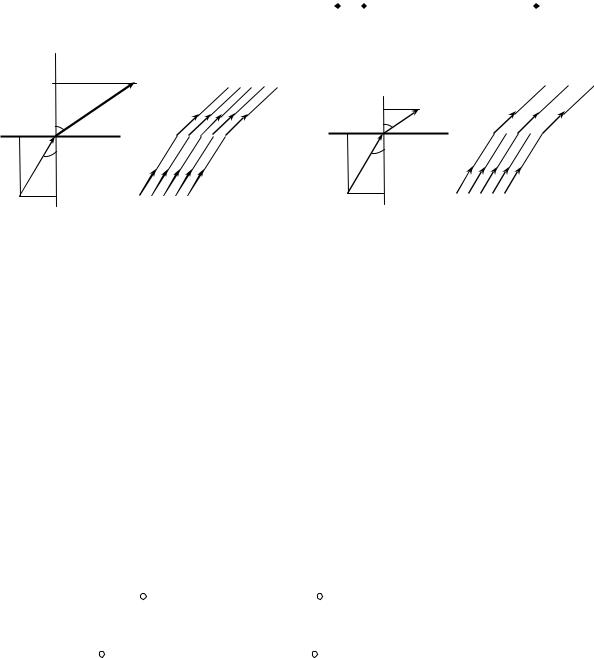
				4		Электродинамика		81
								81
		B2τ
	B2n α2		B2	B2		H2τ	H2
μ2					μ2	H2n α2 H2
μ1	B1				μ1	H1
	α1	B1n			H1n	α1	H1
				B1
	B1τ					H1τ
		(B1n = B2n)				(H1τ = H2τ при jл = 0)
		«а»		«б»		«в»	«г»

Рис. 38

На рис. 38 показана ситуация, когда μ2 > μ1. При μ2 > μ1 получаем соотношение: H2 < H1 и B2 > B1. При отсутствии поверхностных токов на границе раздела магнетиков силовые линии вектора напряженности H магнитного поля разрываются и испытывают преломление (рис. 38-в, г). Силовые линии индукции магнитного поля B на границе раздела магнетиков не испытывают разрыв, а только преломляются (рис. 38-б).

4.7.3. Граничные условия в переменном электромагнитном поле

1. Граничные условия в переменном электромагнитном поле такие же, как и электростатическом и магнитостатическом поле. Покажем это.

Циркуляции вихревого электрического и магнитного полей определяются уравнениями Максвелла:

Ed l = −			∂B dS или	Ed l = −		∂	BdS;
(l )		(S )	∂t	(l )		∂t (S )
Hdl =	j+	∂D	dS или	Hdl = jdS+				∂	DdS.
		∂t
(l )	(S )			(l )	(S )			∂t (S )

Здесь интегралы Фм = BdS и Фэ = DdS − потоки соответствующих по-

(S ) (S )

лей через поверхность, натянутую на контур. При рассмотрении граничных условий в статических полях был взят контур, площадь которого была бесконечно малой. Кроме того, «высота» контура была взята бесконечно малой, т.к. задача состояла в определении условий именно на границе раздела среде. Поступая точно также при определении граничных условий в переменных полях, т.е. выбирая малые контуры, получаем, что в пределе поток электрического и магнитного поля через бесконечно малую поверх-

ность, натянутую на контур,	стремится к			нулю: Фм = BdS = 0
				(S )
и Фэ = DdS= 0. Следовательно, −	∂	BdS= 0 и	∂	DdS= 0.
(S )	∂t (S )		∂t (S )

82	82
	4 Электродинамика

Таким образом, уравнения Максвелла для переменных полей с учетом равенства нулю потоков полей через бесконечно малую поверхность,

примут вид:	Ed l = 0 и	Hdl = jdS=I.
	(l )	(l )	(S )

Эти уравнения для циркуляций аналогичны уравнениям, с помощью которых были получены граничные условия в статических полях. Что и требовалось показать.

Запишем граничные условия в переменных полях (см. § 4.7.1, § 4.7.2). 1. Граничные условия в переменном магнитном поле:

B2n = B1n или μ2μ0H2n = μ1μ0H1n; H2τ − H1τ = jл; при jл = 0 → H2τ = H1τ.

2. Граничные условия в переменном электрическом поле на границе двух диэлектриков:

D2n − D1n = σ или ε2ε0 E2n − ε1ε0 E1n = σ; при σ = 0 → D2n = D1n; E2τ = E1τ.

3. Условия на границе проводник-диэлектрик:

D2n = σ или ε2ε0 E2n =σ,

где: σ − это поверхностная плотность заряда на поверхности проводника. Заметим, что в реальных средах с конечной проводимостью поверхностные токи существовать не могут. Это означало бы, что в бесконечно малом объеме выделяется конечная энергия (например, джоулево тепло), т.е. плотность энергии была бы бесконечно большой. Из этого следует, что на границе раздела реальных сред всегда выполняется непрерывность тан-

генциальных составляющих H и E: H2τ = H1τ; E2τ = E1τ.

2. Соотношение между нормальными составляющими токов проводимости на границе двух сред. При рассмотрении граничных условий учитываются поверхностные электрические токи, т.е. касательная составляющая токов в средах.

Теперь определим соотношение между нормальными составляющими токов проводимости на границе S контактирующих сред.

Допустим, электрический ток распространяется из первой среды во вторую. На рис.39 выделен цилиндр с бесконечно малой высотой, охватывающий обе среды у границы раздела сред. Запишем закон Ома в дифференциальной форме для нормальной составляющей плотности тока

	проводимости:	в первой среде нормальная состав-		j2
	ляющая вектора плотности тока j1n = g1E1n; во второй		n		S
	среды j2n = g2E2n. В этих уравнениях g1 и g2 − прово-
	димость контактирующих сред ( обратная величина			j1
	удельного сопротивления). Из уравнения непрерыв-		Рис. 39
	ности jdS=− dq следует, что поток плотности тока
	(S )	dt

4 Электродинамика	83
	83

проводимости j из объема цилиндра равен свободным зарядам, выходящим за единицу времени через поверхность цилиндра, т.е. равен убыли заряда в единицу времени внутри цилиндра. Нормальная составляющая вектора j перпендикулярна торцевым поверхностям цилиндра и для этой составляющей из уравнения непрерывности получим:

(g2E2n	− g1E1n) S = −	dq	или	g2E2n − g1E1n	=−	dσ	.	(4.67)
		dt
						dt
(σ – поверхностная плотность заряда на				S).

Допустим, электромагнитное поле в контактирующих средах синусоидальное. Уравнение (4.67) в установившемся режиме электромагнитного поля можно записать в комплексной форме (§ 4.6):

	−			(4.68)
g2 E 2n		g1 E1n = − iωσ

(множитель eiωt , зависящий от времени t, сокращается). Напомним, величины со «крышкой» – это комплексные амплитуды, зависящие только от координат. Из (4.68) следует, что при наличии нормальной составляющей электрического тока на границе раздела сред, на этой границе возникает поверхностный заряд. Есть одно исключение.

Запишем граничное условие ε2ε0 E2n − ε1ε0 E1n = σ в комплексной форме:

				(4.69)
ε2ε0 E 2n − ε1ε0	E1n	=	σ

Рассматривая совместно (4.68) и (4.69) получим, что при строгом выполнении соотношения (ε1ε0g2 = ε2ε0g1) поверхностные заряды на границе будут отсутствовать. Впрочем, это соотношение на практике редко осуществляется.

4.8. Электромагнитная волна в среде с проводимостью

4.8.1. Комплексная диэлектрическая проницаемость

1. Реальная среда в той или иной степени обладает проводимостью, т.к. в любой реальной среде содержится некоторое количество свободных зарядов. По проводимости среды делятся на проводники, полупроводники и диэлектрики. Вспомним курс общей физики. Энергетический спектр электронов в кристаллах имеет зонную структуру, и с позиции зонной теории проводимость сред количественно оценивается по энергетической ши-

рине ε последней запрещенной зоны (запрещенная зона находится между валентной зоной и зоной проводимости). Валентные электроны могут покидать свои атомы, если электроны приобретут достаточную энергию для преодоления потенциального барьера запрещенной зоны, и «принять участие» в электрическом токе.

84	84
	4 Электродинамика

В проводниках (например, в металлах) валентная зона и зона проводимости перекрываются, и валентные электроны в металлах уже при температурах близких к 0 К находятся в зоне проводимости. Металлы являются хорошими проводниками. Условно принято, что полупроводниками являются материалы, у которых ширина последней запрещенной

зоны ε < 2 эВ. Например, ширина запрещенной зоны известных полу-

проводниковых кристаллов кремния Si и германия Ge ε ≈ 1 эВ. К диэлектрикам (диэлектрики называют еще изоляторами) относятся материа-

лы, ширина последней запрещенной зоны которых ε > 2 эВ. Однако, несмотря на довольно большую энергетическую ширину последней запрещенной зоны диэлектриков, статистически в межатомном пространстве реальных диэлектриков все же содержится некоторое количество свободных электронов, поэтому и диэлектрики обладают проводимостью, хотя и незначительной. Итак, соотношение между проводимостями ди- неравенствомэлектриков gд:., полупроводников gпп. и проводников gпр можно выразить

gд. << gпп < gпр.,

(напомним, g = 1r , где r – удельное сопротивление среды).

2. Классификация сред на проводники и диэлектрики с позиции электродинамики определяется по относительному значению тока проводимо-

сти j = gE и тока смещения jсм. = ∂∂Dt =εε0 ∂∂Et . Ток проводимости gE обуслов-

ленным движением свободных зарядов, ток смещения ∂∂Dt обусловленным переменным электромагнитным полем. Если в среде gE >> εε0 ∂∂Et , то та-

кая среда является проводником, если gE << εε0 ∂∂Et , то среда является

диэлектриком. При условии, когда gE и εε0 ∂∂Et одного порядка, то та-

кую среду будем называть полупроводником.

Важно в приведенных оценочных неравенствах обратить внимание на то обстоятельство, что соотношение между током проводимости j и током смещения jсм зависит не только от параметров среды g и ε, но и от бы-

строты изменения электрического поля электромагнитной волны − зависит также и от значения ∂∂Et , т.е. от частоты колебаний вектора E.

Допустим, электромагнитная волна является синусоидальной. Запишем уравнение Максвелла для ротора комплексной амплитуды H (§ 4.6):

			или
[ ,H] = j		+ iωεε0 E		[ ,H] = (g + iωεε0 )E.

4 Электродинамика	85
	85

Последнее уравнение можно представить в виде:

								g
	[ ,H] =iω				εε0	−i				E.	(4.70)
								ω
	Комплексная величина:					g
	ε	=	εε		−i						(4.71)
				0
	к
						ω
	называется комплексной диэлектрической проницаемостью.
											будем иметь уравнение
	Итак, вместо уравнения [ ,H] =				j + iωεε0					E
											(4.72)
	[ ,H] =iω εк E.

Уравнение (4.72) позволяет рассматривать любую среду как диэлектрик с комплексной диэлектрической проницаемостью εк. Соотношение между

вещественной частью εε0 и мнимой ωg комплексной диэлектрической проницаемости εк определяет свойства среды:

-при g >> εε0ω среда является проводником;

-при g << εε0ω среда является реальным диэлектриком.

	При граничной частоте	ωгр. =	g		(4.73)
			εε	0

амплитуды тока проводимости и тока смещения равны. При высоких частотах электромагнитной волны (ω >> ωгр.) основную роль играют токи смещения, и среда при этих частотах рассматривается как диэлектрик; при низких частотах волны (ω << ωгр.) основную роль играют токи проводимости, и среда при этих частотах рассматривается как проводник.

Например, проводимость меди g = 5,7 107 Сим/м, диэлектрическая проницаемость металлов того же порядка, что и диэлектрическая прони-

цаемость воздуха ε ~ (1 10). Если принять ε				= 10, то имеем:
fгр. =	ωгр.	=	5,7 107		= 10	17	Гц.
	2π		2 3,14 10 0,885 10−11

Полученная частота находится в ультрафиолетовом диапазоне электромаг-

нитных волн ( длина волны 3 10-9м). В радиодиапазоне ( радиодиапазон простирается до частот 1013 1014 Гц) металлы являются проводниками. Таким образом, в металлах в радиодиапазоне частот ток проводимости превышает ток смещения более чем в 103 раз. Для пресной воды (g = 10 -3

Сим/м, ε = 81) граничная частота fгр. = 2 105 Гц; для морской соляной воды

(g = 4 Сим/м, ε = 81) fгр. = 109 Гц.

86	86
	4 Электродинамика

В нелинейных магнетиках (например, в ферромагнетиках) возможны магнитные потери и магнитная проницаемость становится комплексной

величиной μк, и уравнение для ротора вектора комплексной амплитуды E

запишется в виде:			(4.74)
	[ ,E] = iωμк H.

В дальнейшем будем рассматривать линейные магнетики с постоянной магнитной проницаемостью и в отсутствии магнитных потерь в среде.

Умножив (4.72) и (4.74) на eiωt , получим уравнения Максвелла для роторов комплексных функций Eк и Hк в среде с проводимостью:

[ , Hк] =iω εк Eк,	(4.75)
[ , Eк] = iωμμ0 Hк,	(4.76)
а также уравнения для дивергенций:
Hк = 0 и Eк = 0.	(4.77)

4.8.2. Уравнение плоской волны в среде с проводимостью

Прежде чем рассматривать содержание данного параграфа, рекомендуем еще раз перечитать § 4.5.1 и 4.5.2, где приводятся волновые уравнения вещественных векторов E и H в идеальном диэлектрике и решения этих уравнений.

В идеальном диэлектрике волновое уравнение (4.40) получено из анализа уравнений Максвелла (4.26). Решением волновых уравнений являются уравнения волны (4.44*) и (4.45*), которые представим в ком-

плексной форме, выделив отдельно множитель e−ikz , зависящий от координаты:

			Eк =			E0eiϕ e−ikz eiωt					(4.78)
								=E e−ikz eiωt ;
									E
			H = H	0	eiϕ e−ikz eiωt =H e−ikz eiωt =					e−ikz eiωt ,	(4.79)
			к						Z0
где Z0 =	E0	=	μμ0 , k = 2π			= ω .	Так как фазовая скорость волны в ди-
	H 0		εε0	λ		v
электрике определяется выражением v =								1	, то волновое число мож-
								εε0μμ0
но записать в виде k = ω					εε0μμ0 .		Уравнения (4.78) и (4.79) описывают

электромагнитную волну, распространяющуюся в положительном направлении оси 0Z, на это указывает знак минус в сомножителе e−ikz .

Среда с проводимостью. Структура уравнений Максвелла для комплексных функций Eк и Hк в среде с проводимостью (4.75, 4.76, 4.77) одинакова со структурой системы уравнений Максвелла (4.26) в идеальном диэлектрике. Следовательно, решения E к и Hк в среде с проводимостью

4 Электродинамика	87
	87

будут иметь вид, аналогичный уравнениям (4.78) и (4.79) с учетом того,

что в среде с проводимостью диэлектрическая проницаемость εк – комплексная величина. В решении волнового уравнения для среды с проводимостью вещественное волновое число k (вещественный фазовый множи-

тель) следует заменить комплексной величиной k − комплексным фазовым множителем, а вещественное волновое сопротивление Z0 заменить ком-

плексным волновым сопротивлением Z 0 :

= ω = ω

, где

1

− комплексная фазовая скорость;

k

ε

к

μμ

0

v =

εкμμ0

v

Z 0 =

μμ0 .

E =

ε к

H

Запишем уравнения волны комплексных функций напряженности электрического поля Eк и напряженности магнитного поля Hк в среде с проводимостью

				(4.80)
	Eк =E e−i k z eiωt ;
		E
	Hк =		e−i k z eiωt ,	(4.81)
		Z0

Проведем анализ уравнений (4.80) и (4.81).

1.	Комплексная величина		, как любая комплексная величина,	может
		k
быть представлена в виде:
				(4.82)
			k = k − iα
Подставим (4.82) в (4.80), получим:
				(4.83)
		Eк =E e−α z e−ikz eiωt .

Пусть начальная фаза E равна нулю, тогда это уравнение в тригонометрической форме имеет вид:

Ex = E0e−α z cos (ωt − kz)

(4.83*)

(напомним, в этой записи принято, что плоская волна распространяется в положительном направлении оси 0Z, вектор E колеблется по оси 0X,

вектор H − по оси 0Y).

Из (4.83) следует, что положительная величина α ( мнимая часть

комплексного фазового множителя k ) определяет затухание амплитуды волны с расстоянием по мере удаления электромагнитной волны от источника волны и называется коэффициентом затухания. В эксперимен-

тальном плане α равна обратной величине некоторого расстояния l0,

88	4 Электродинамика	88
на котором амплитуда волны E0 e−α z уменьшается в e ≈ 2,7 раз: α =		1	.
		l0

Ясно, что механизм потерь электромагнитной энергии в проводящей среде обусловлен возбуждением в среде электрических токов с последующим выделением джоулевого тепла.

Величина k имеет тот же смысл волнового числа, что и в уравнении волны в идеальном диэлектрике: k = 2λπ . Как и в идеальном диэлектрике, в среде с проводимостью волновое число k определяет фазовую скорость волны: v = ωk . Фазовая скорость – это скорость распространения

волновой поверхности ( например, передней волновой поверхности − фронта волны).

2. Комплексное волновое число представим в форме Эйлера (через экс-

поненту): Z 0 =Z0 eiϕ . Здесь Z0 − модуль, ϕ − аргумент волнового сопротивления. Тогда уравнение волны для комплексной функции напряженности магнитного поля запишется как:

Hк =	E	e−i kz eiωt =	E	e−α z e−ikz ei(ωt −ϕ ) .	(4.84)

Z0 Z0

В обычной тригонометрической записи уравнение волны для напряженности магнитного поля электромагнитной волны в среде с проводимостью

	примет вид:	Hy =	E0	e−α z cos (ωt − kz − ϕ).	(4.85)
			Z0

Из сравнения уравнений (4.83) и (4.85) следует, что в среде с проводимостью имеется сдвиг фаз между электрическим и магнитным полями электромагнитной волны. Напомним, в идеальном диэлектрике фазовый сдвиг между векторами E и H отсутствует (§4.5.2).

Воспользовавшись соотношениями для комплексного фазового множителя и комплексного волнового сопротивления

k	= ω ε μμ		= k − iα и	Z 0 = μμ0	= Z eiϕ , где	ε = εε			− i g ,
	к	0		ε к	0	к		0
										ω

можно получить оценочные формулы для вещественных величин: коэффициента затухания α; вещественного фазового множителя k; фазовой

скорости v; модуля аргумента волнового сопротивления Z0; сдвига фаз ϕ между E и H. Вывод основывается на возведение в квадрат первого соотношения и последующего приравнивания действительной и мнимой частей полученного равенства. Вывод оценочных формул несложный, и подробности вывода здесь опустим. Приведем результаты для двух случаев.

4 Электродинамика	89
	89

А. Среда − реальный диэлектрик (εε0ω >> g − среда обладает незначи-

тельной проводимостью):

- волновое сопротивление:

Z0 =

(μμ0 )2

≈

μμ0

(εε0 )2 + g 2

εε0

ω2

- коэффициент затухания:

α2 = ωεε μμ

1

+

1

1

+

g 2

≈

g 2μμ0

или

0

0 −

2

2

(εε0 )2ω

2

4εε0

α ≈

g

μμ0

=

g

Z0;

2

2

εε0

- фазовой множитель:

k = ωεε μμ

1

+

1

1

+

g 2

≈ ω

εε

μμ

;

0

0

2

2

(εε0 )2

ω2

0

0

- фазовая скорость волны:	v = ω	=	2α		≈	1	;
			μμ0g
	k					εε0μμ0
- сдвиг фазы между E и H:	ϕ = arctg α				≈ 0.
			k

Из приведенных оценок следует, что в реальном диэлектрике с незначительной проводимостью результаты такие же, что и в идеальном диэлек-

трике. В реальном диэлектрике коэффициент затухания α не зависит от частоты, а определяется проводимостью g и волновым сопротивлением Z0.

Б. Среда − проводник. С учетом соотношения для хорошо проводящей среды g >> εε0ω , получим:

- волновое сопротивление:	Z0 ≈			μμ0ω			;
				g
- коэффициент затухания:	α ≈		μμ0gω				;
		2
- фазовой множитель:	k ≈		μμ0gω					;
		2
- фазовая скорость волны:	v ≈			2ω	;
		μμ0g
- сдвиг фазы между E и H:	ϕ = arctg αk ≈ π4 .

Из полученных оценок следует, что в проводящей среде:

1)происходит поглощение энергии электромагнитной волны, и это поглощение можно характеризовать коэффициентом затухания ампли-

туды волны в проводящей среде, причем в проводниках α ≈ k (напомним, в курсе общей физики было показано, что энергия электромагнитной волны определяется квадратом амплитуды E и H). Например, в меди при обычной радиотехнической частоте f = 100 МГц (длина волны 3 м) α ≈ 15 104 м−1 , следовательно, при прохождении

90	90
	4 Электродинамика

волной расстояния l0 = α1 ≈ 7 10−6 м = 7 10−3мм амплитуда в проводящей среде уменьшается в e = 2,7 раз;

2)фазовая скорость v очень мала. Например, в меди v ≈ 4 102 м/с (сравните, в вакууме v ≈ 3 108 м/с);

3)волновое сопротивление Z0 проводников очень мало. Например, волновое сопротивление меди ≈ 4 10−3 Ом (сравните, волновое сопро-

тивление вакуума ≈ 380 Ом). Уже из этого следует, что в проводящей среде перенос энергии осуществляется в основном магнитным полем электромагнитной волны (см. определение волнового сопротивления). Приведем оценку данного эффекта, для чего сравним максимальную плотность энергии магнитного и электрического поля электромагнитной волны в проводящей среде:

	w		μμ	H 2		μμ	H 2			μμ			0
	м =		0	0	=	0	0		=					.
						εε H 2Z		2		εε		Z 2
	w	э	εε E2								0
			0	0		0	0	0					0
Например, для меди	wм ≈ 3 107, т.е. практически вся энергия элек-
	wэ

тромагнитного поля в проводнике сосредоточена в магнитном поле

(при вычислении принято, что магнитная проницаемость μ и диэлектрическая проницаемость порядка металлов порядка проницаемости воздуха, т.е. ~ 1);

4)в проводниках фазы колебаний векторов E и H не совпадают.

4.9.Энергетические соотношения в электромагнитной волне

Впредыдущих параграфах мы выяснили, что переменное электромагнитное поле всегда находится в движении в виде электромагнитной волны (электромагнитного излучения). Электромагнитная волна как материальный объект обладает энергией и переносит энергию в среде своего распространения.

4.9.1. Поток плотности электромагнитной энергии, вектор Пойнтинга

Плотность энергии. Энергия электромагнитного поля локализована в пространстве. Плотность энергии определяет энергию в единице объема:

w = WV ,

которая складывается из плотности энергии электрического и магнитного полей:

w = wэ + wм =	εε0E2	+	μμ0H 2	,	(4.86)
2		2