5. Статические погрешности измерений

Статическими погрешностями измерения называют погрешности, возникающие при определении постоянного во времени измеряемого значения. При этом предполагается, что все переходные процессы в измерительном устройстве завершены; следовательно, измерительный прибор и измеряемая величина находятся в установившемся состоянии.

5.1. Виды погрешностей

Если при указанных выше условиях проводить многократные независимые измерения, то возникает ситуация, при которой можно различать два принципиально отличающихся вида погрешностей, так называемые систематическиеислучайныепогрешности.

Систематическую погрешность Е_s определяют как отклонение действительного измеряемого значения от среднего значения (математического ожидания):

Е_s =-х

Математическое ожидание является средним значением бесконечного числа измерений:

=_ai /n

При одинаковых условиях эта погрешность всегда имеет ту же самую абсолютную величину и тот же самый знак.

В противоположность этому ни абсолютная величина, ни знак отклонения отдельного измерения от математического ожидания не могут быть предсказаны заранее. Эта случайная погрешность обозначается через Е_s. Она соответствует разности между показанием единичного измерения и математическим ожиданием:

Е_аi = х_аi -

Различию в природе обоих видов погрешности соответствуют разные способы их описания.

5.2. Случайная погрешность отдельного измерения

Колебания случайной погрешности, кажущиеся сначала совершенно беспорядочными, тем не менее, подчиняются в статистическом смысле известным законам.

Если показания какого-либо измерительного прибора, являющиеся сами по себе непрерывными, разбить на интервалы определённой ширины и вычислить относительную частоту попадания показаний в отдельные интервалы при повторных измерениях, то можно получить гистограмму.

При достаточно большом значении nэто изображение является представительным, т.е. относительная частота стремится к некоторому пределу и перестаёт зависеть отn.

Если имеется достаточно большое число показаний, то можно улучшать гистограмму, уменьшая ширину интервалов . Тогда при предельном переходеиnступенчатая функция гистограммы переходит в общем случае в непрерывную функцию – плотность распределения (плотность вероятности, дифференциальную функцию распределения)h ()

h ()=

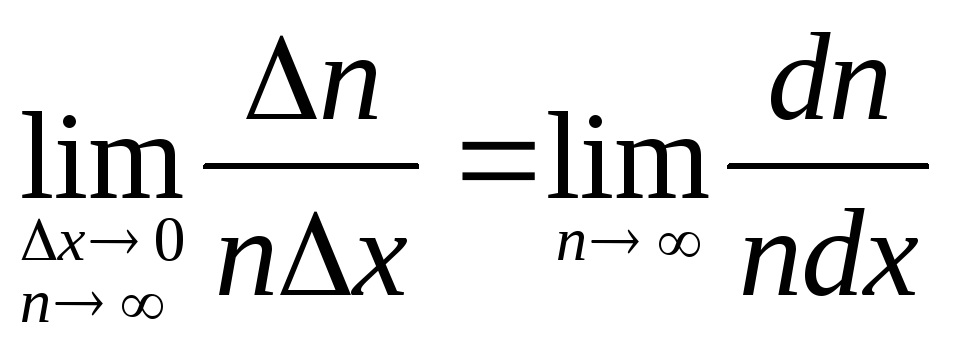
Основываясь на определении плотности распределения, можно установить её прямую связь с функцией распределения. Вероятность того, что измеряемое значение попадает в интервал ₁<xx₂, определяется площадью F, лежащей под графиком плотности распределения вероятности в этом диапазоне:

P (₁ <  ₂) =

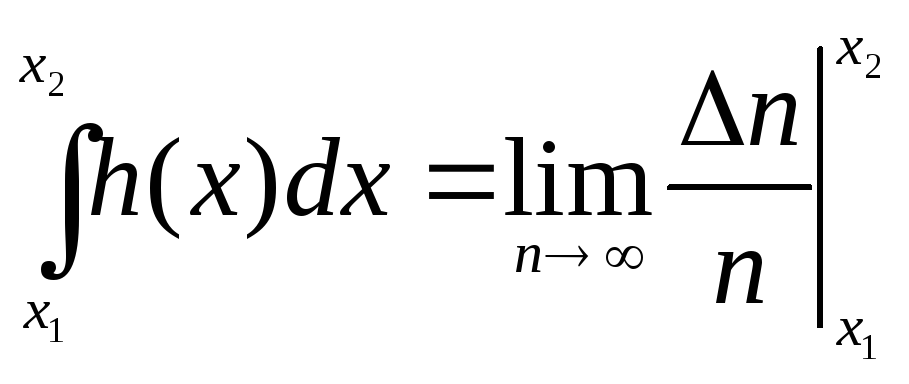
В частном случае имеем

P (- < +) =

Часто при обработке результатов измерения представляет интерес вероятность того, что измеренная величина окажется меньше заданного предела ₁:

P () = P (  ₁)= .

При - < +функция распределения изменяется от0до 1. В связи с тем, что функция распределенияР()определяется как интеграл плотностиh(), её часто называют также интегральной функцией распределения.

Аналогичным образом определяется вероятность того, что измеренная величина окажется больше, чем ₁:

P ( > ₁) =

Среди множества функций распределения особое место для измерительной техники занимает нормальное распределение (распределение Гаусса).

Плотность вероятности нормального распределения определяется следующим уравнением:

h ()= -< +

Нормальное распределение характеризуется, кроме математического ожидания , ещё только одним параметром - среднеквадратичным (стандартным) отклонением.

При известном среднеквадратичном отклонении можно вычислить вероятность того, что случайная погрешностьЕ_аi– отклонение показания отдельного измерения от математического ожидания – будет меньше заданного граничного значенияс. Эта вероятность

Р(с) = 2

называется доверительной вероятностью (статистической надёжностью).

При известном значении (рис.5.1) можно на основании единственного измерения указать верхнюю и нижнюю границы математического ожидания:

или

Математическое ожидание с доверительной вероятностью Р(%)лежит внутри этих границ. Интервал между этими границами называетсядоверительным интервалом математического ожидания.

Математическое ожидание определяется следующим образом:

Эта величина соответствует первому моменту плотности распределения – абсциссе центра тяжести площади между зависимостью плотности распределения и осью абсцисс.

Площадь фигуры, очерченной зависимостью , равна единице.

В качестве оценки для используется среднее значение:

Среднеквадратичное отклонение определяется из формулы

Величина , называемаядисперсией,соответствует второму моменту («моменту инерции») плотности распределения вероятностей.

В качестве оценки среднеквадратичного отклонения используется рассеяниеS, определяемое по формуле