2.8. Равномерное распределение

Определение: Непрерывная случайная величина имеетравномерное распределение на отрезке , если ее плотность имеет вид:

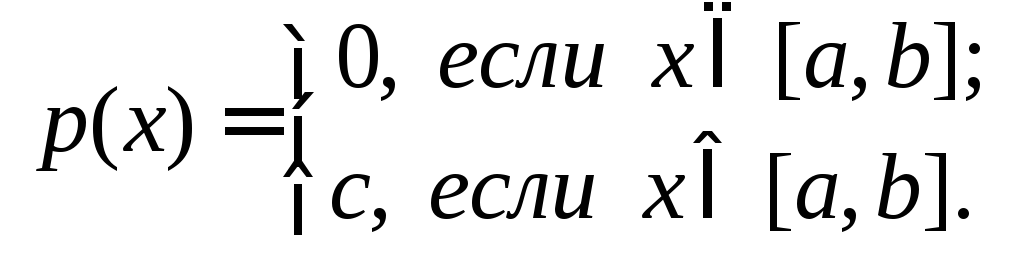(18)

График плотности равномерного распределения изображен на рис. 8.

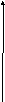
Рис.8.

Теорема. Если непрерывная случайная величина имеет равномерное распределение на отрезке , то:

; ;.

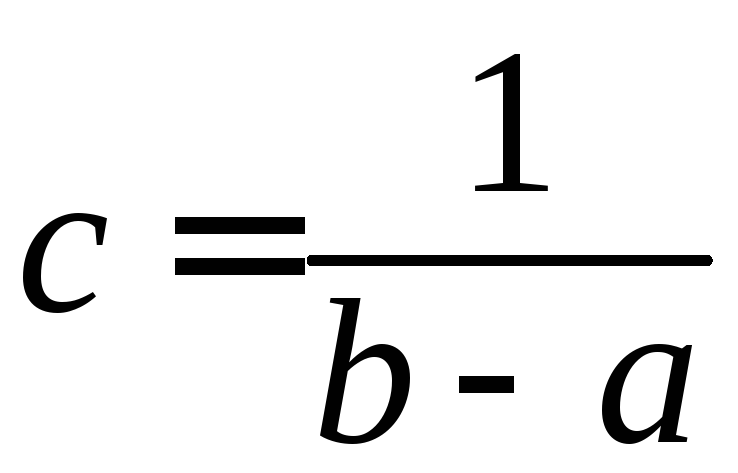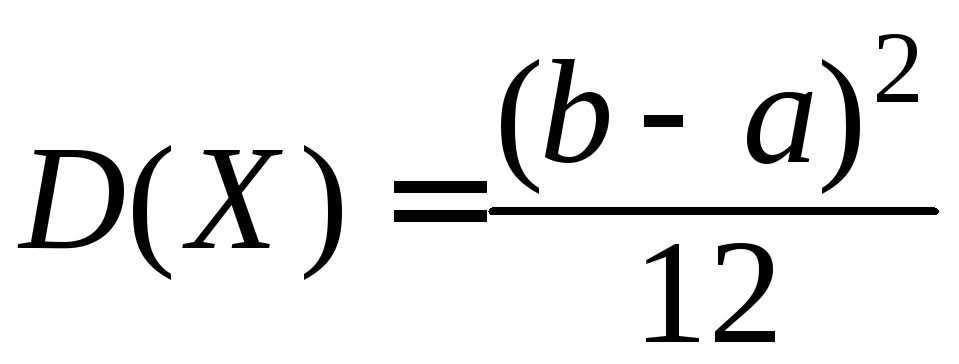Замечание. Число 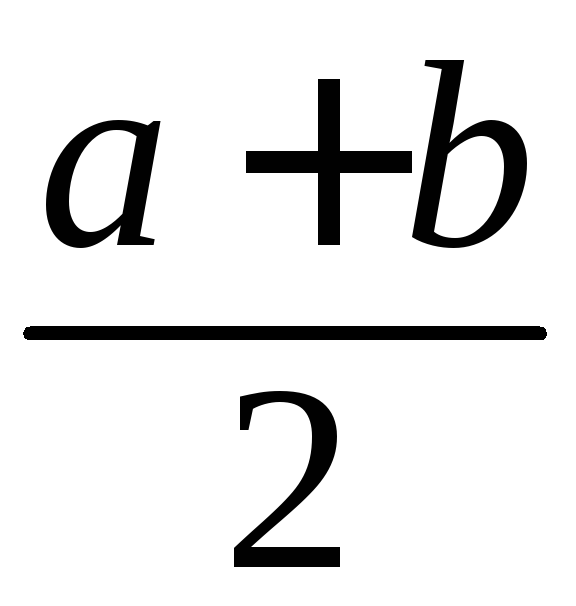— середина отрезка; число— длина отрезка;

Доказательство. Для определения параметра воспользуемся свойством плотности (10):

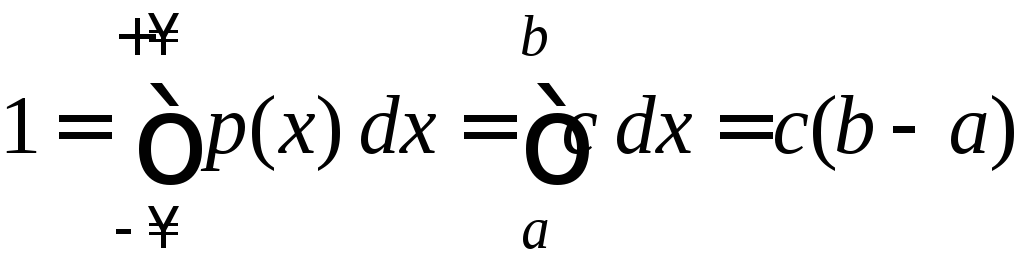, откуда .

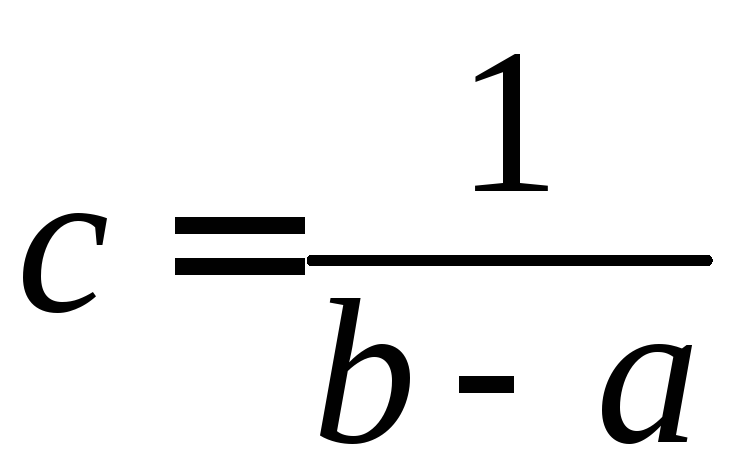Далее,

.

. ▄

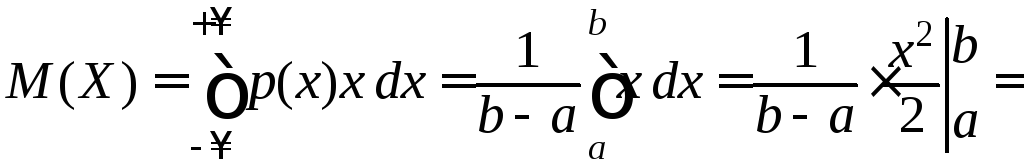
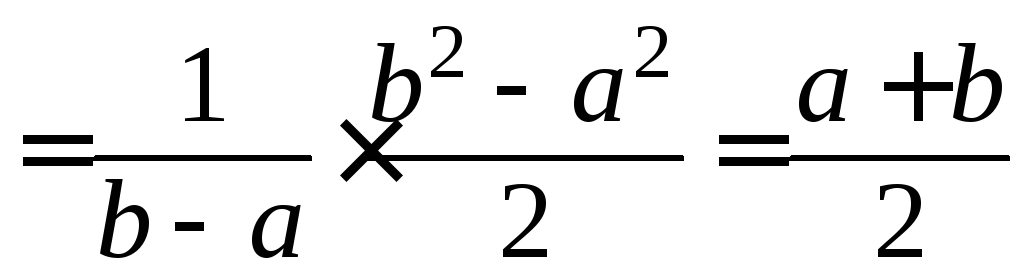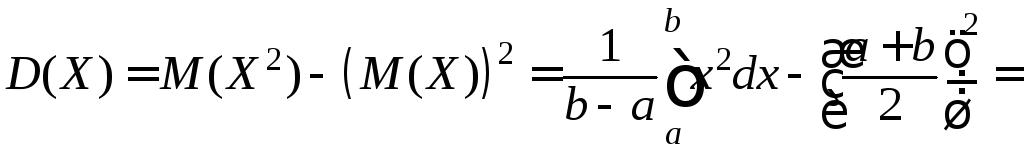
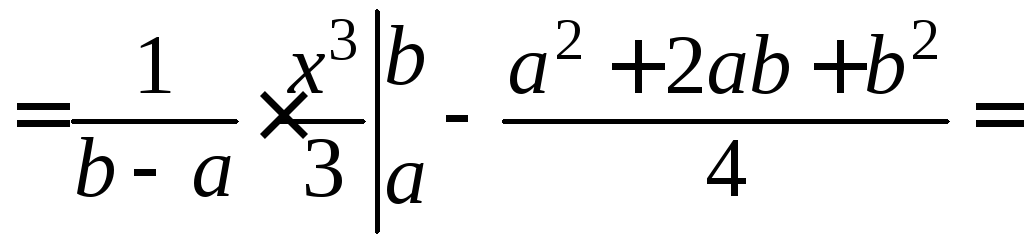
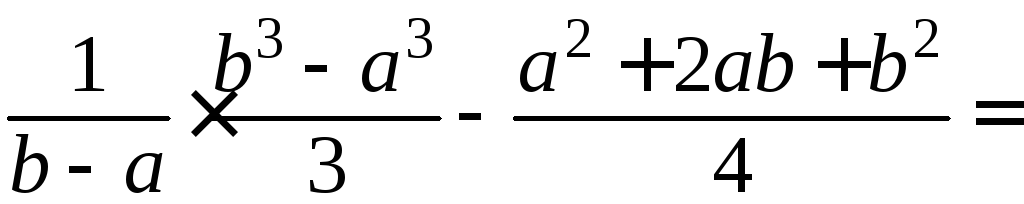
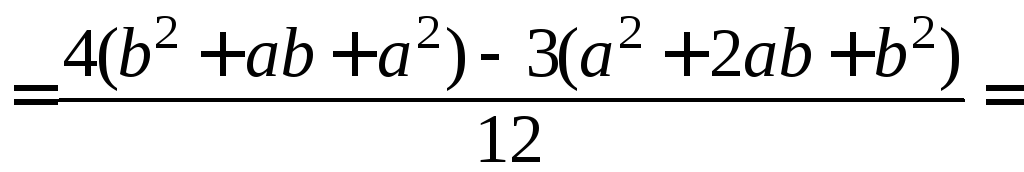
Замечание. Полученные значения математического ожидания и дисперсии равномерного распределения хорошо иллюстрируют их статистический смысл.

Так, в силу симметрии графика плотности относительно середины отрезка, при большом числе реализаций случайной величины одинаково часто будут встречаться значения случайной величины с обеих сторон от этой середины. Поэтому среднее арифметическое должно оказаться близким к ней.

Чем больше длина отрезка, то есть число , тем на большем промежутке «размазаны» возможные значения, тем больше должна быть дисперсия, которая как раз и пропорциональна квадрату длины отрезка.

Аналогичными вычислениями получается выражение для функции распределения равномерного распределения:

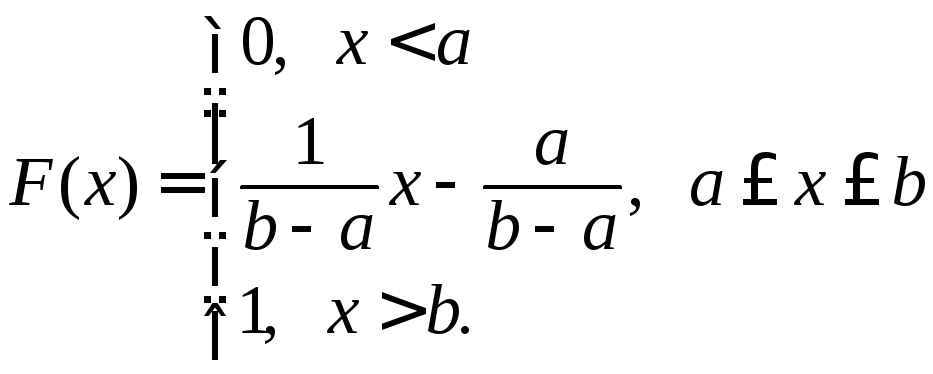
2.9. Преобразование случайных величин

I. Линейное преобразование нормального закона.

Теорема. Если случайная величина распределена по нормальному закону с параметрамии, то прислучайная величина, полученная излинейным преобразованием вида, также имеет нормальное распределение с параметрамии.

Доказательство. Рассмотрим случай . Тогда функциястрого возрастает, и имеет место равносильность неравенств:

.

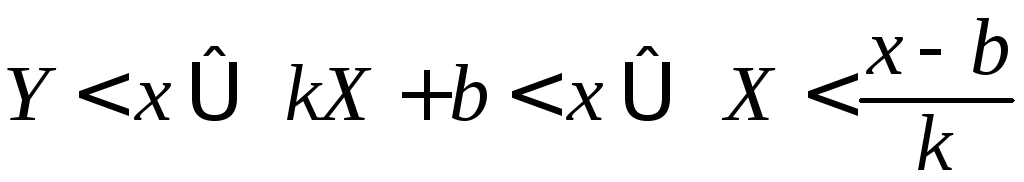Поэтому также имеет место равенство событий:

.

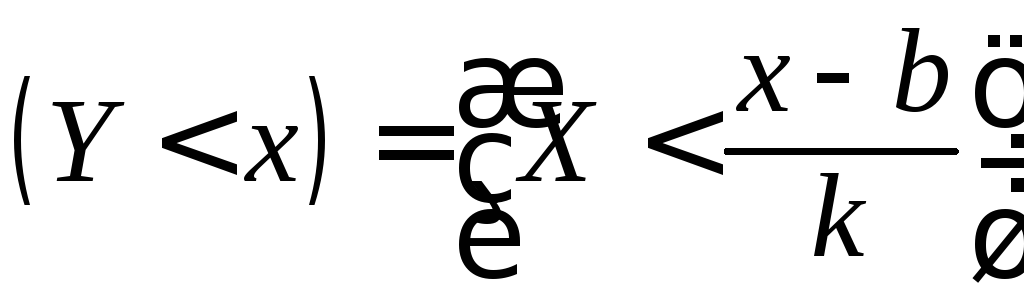Найдем функцию распределения случайной величиныи убедимся, что она соответствует нормальному распределению.

.

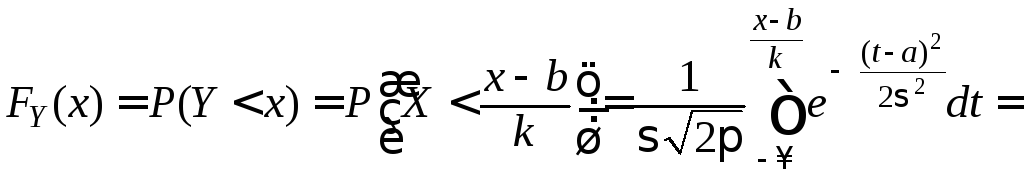
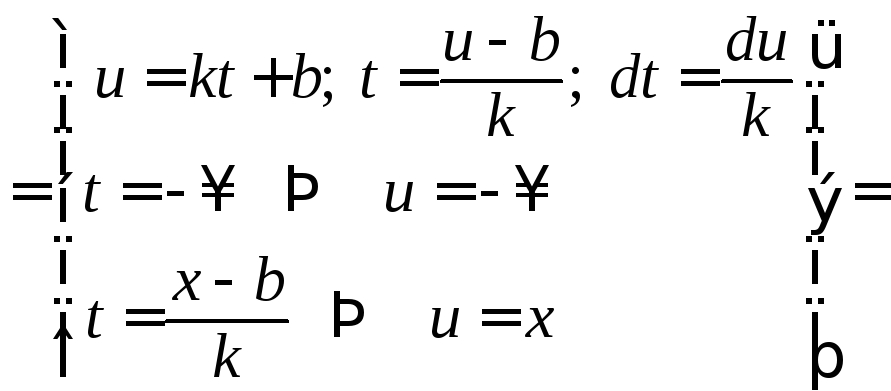
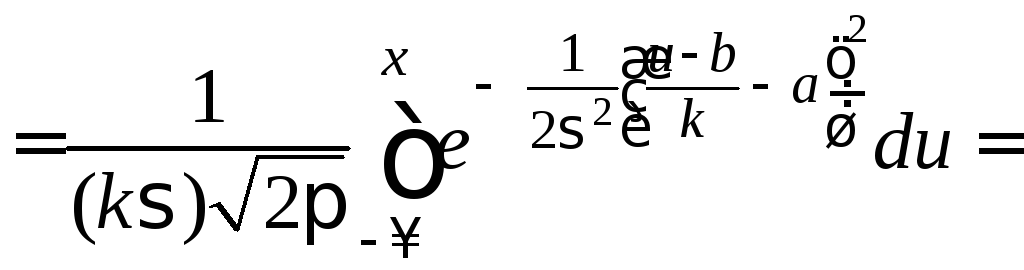
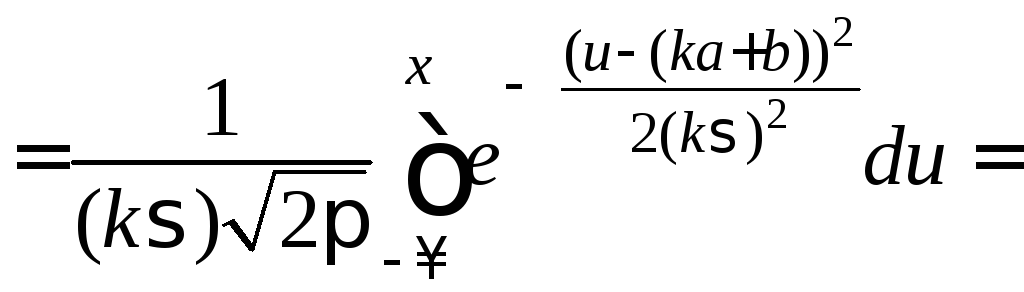
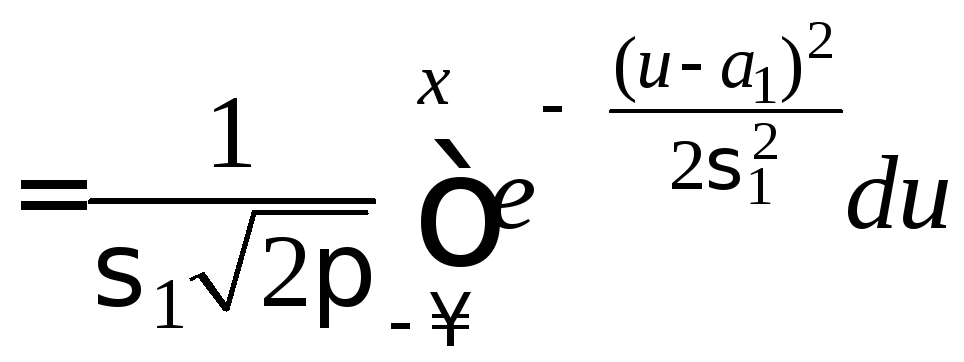Пришли к функции распределения нормального закона с параметрами и. Аналогично рассматривается и случай. ▄

II. Общий случай преобразования случайной величины.

Пусть теперь – не линейная, а произвольная непрерывнаястрого монотонная функция. Аналогичными выкладками можно при заданных функции распределения и плотностислучайной величинынайти функцию распределенияи плотностьслучайной величины. Дело сводится к замене переменной в соответствующем интеграле.

Пример. Пусть , то есть. Из равносильности неравенств:вытекает равенство событий:. Поэтому

.

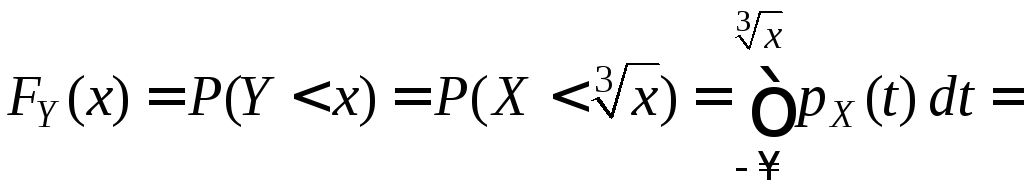
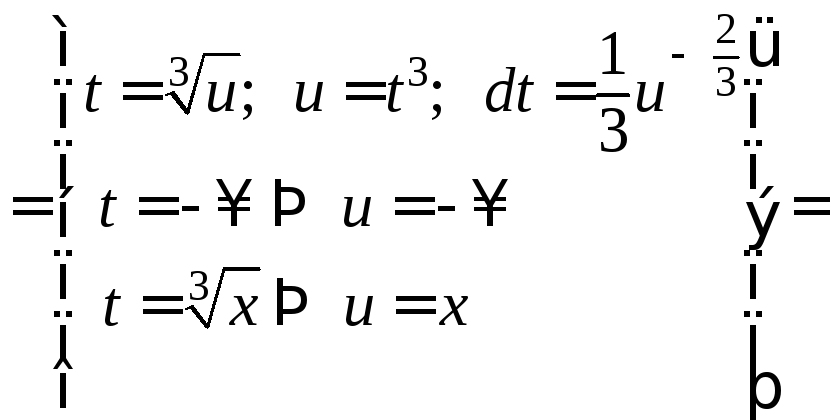
Подынтегральная функция в последнем выражении является плотностью распределения случайной величины :.

2.10. Вероятность попадания в промежуток для нормального распределения.

I. Вероятность попадания в произвольный промежуток.

Теорема. Пусть непрерывная случайная величина имеет нормальное распределение с параметрамии. Тогда для всякого промежуткавероятность попадания значенияв этот промежуток задается формулой:

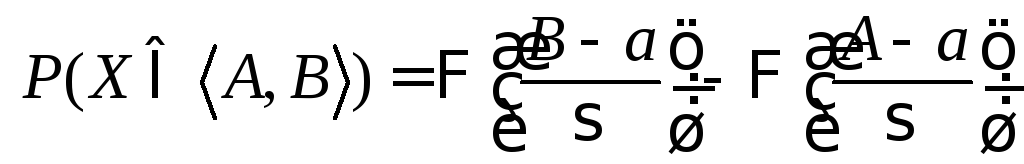. (19)

Доказательство. Поскольку для непрерывной случайной величины вероятность попадания в промежуток не зависит от типа промежутка (п. 2.2), докажем формулу (19) для интервала . Введем случайную величину

.

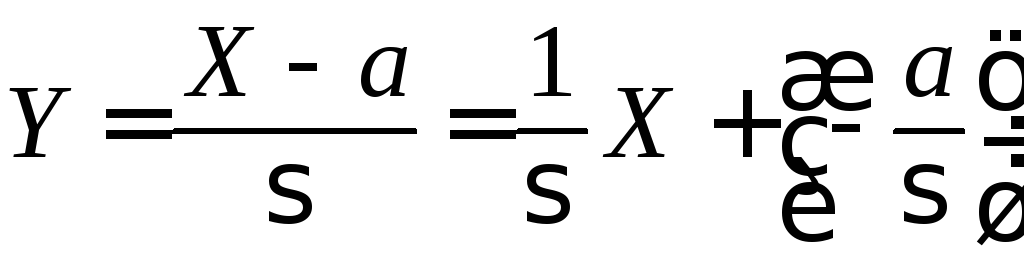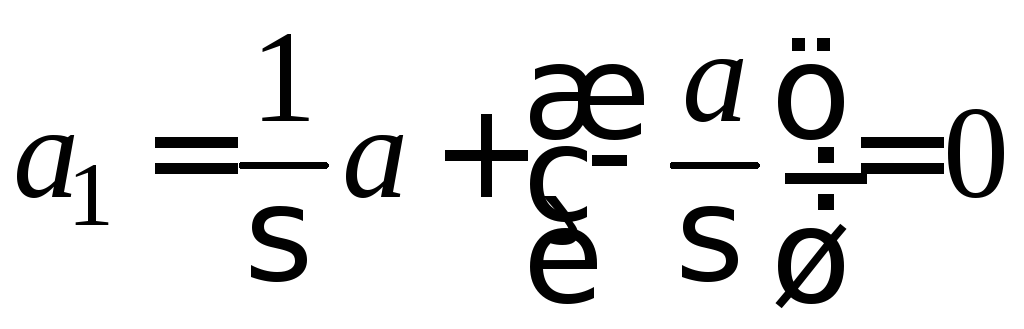Она получена из линейным преобразованием. По предыдущей теоремеимеет нормальное распределение с параметрамии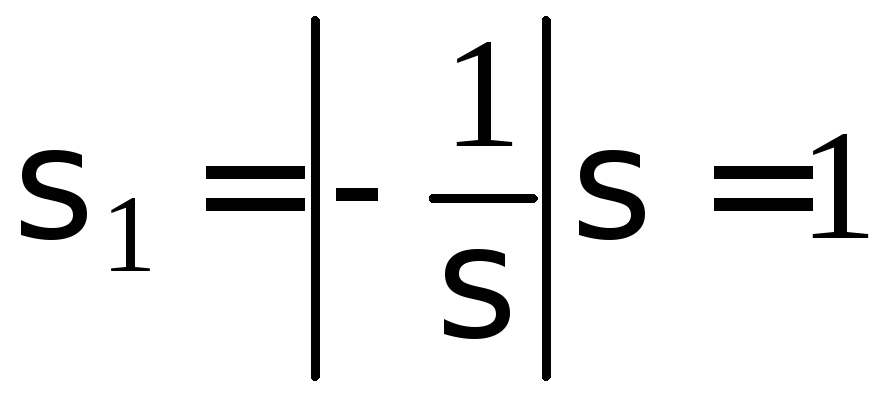. Ее плотностью является дифференциальная функция Лапласа, одной из первообразных которой является интегральная функция Лапласа.

Ввиду равносильности неравенств

,

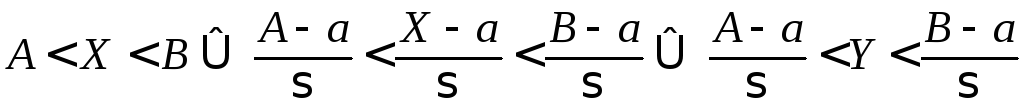получаем для вероятностей:

.

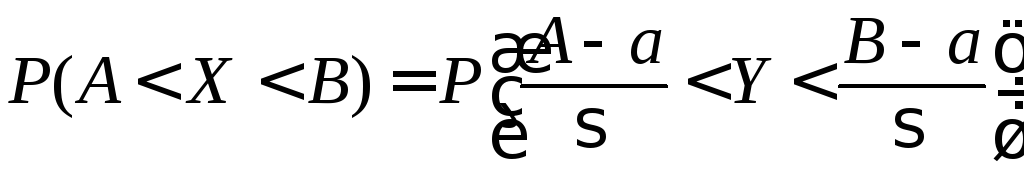
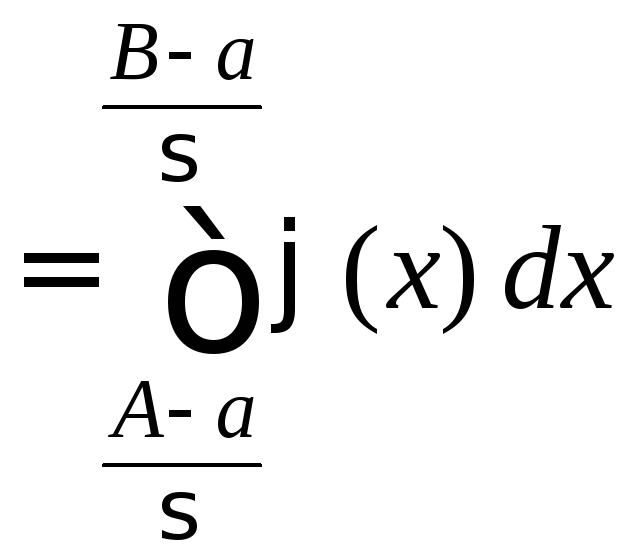Применяя к последнему интегралу формулу Ньютона-Лейбница с первообразной , получаем окончательно:

. ▄

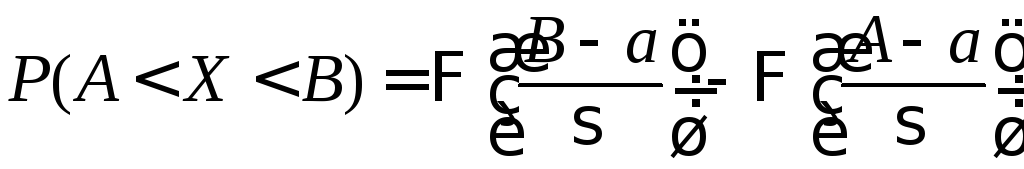Пример. Пусть имеет нормальное распределение с параметрамии. Найдем вероятность попадания в отрезок.

Здесь 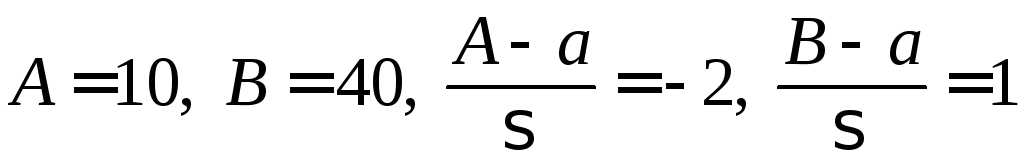. Учитывая нечетность функции, получаем:

.

В соответствии с эмпирическим законом больших чисел, следует ожидать, что при большом числе испытаний относительная частота попадания реализованного значения случайной величины в отрезок окажется близкой к 82%.