
- •Функция многих переменных: определение, геометрический смысл, область определения, область значений, линия уровня, поверхность уровня.
- •Частные приращения функции двух аргументов, частные производные первого порядка, частные производные высших порядков
- •Сложные функции и их дифференцирование.
- •Неявные функции и их дифференцирование.
- •Экстремум функции двух переменных, условный экстремум, наибольшее и наименьшее значение функции в замкнутой области.
- •Полное приращение и полный дифференциал функции двух аргументов первого порядка. Применение полного дифференциала к приближенным вычислениям.
- •Дифференциалы высших порядков от функции двух аргументов.
- •Касательная плоскость и нормаль к поверхности в заданной точке.
- •Скалярное поле, производная по направлению, градиент, их свойства.
- •Первообразная. Неопределенный интеграл: его свойства, геометрический смысл.
- •Интегрирование тригонометрических функций
- •Интегрирование дробно-рациональных функций.
- •Интегрирование некоторых трансцендентных функций.
- •Интегрирование простейших иррациональных алгебраических функций.
- •Интегрирование гиперболических функций
- •Интегральная сумма, определенный интеграл (определение, теорема существования, основные свойства, правила вычисления)
- •Геометрические приложения определенного интеграла: вычисление площади плоской фигуры, длины дуги плоской кривой, объема тела.
- •Физические приложения определенного интеграла: статические моменты и моменты инерции плоских дуг и фигур, нахождение координат центра тяжести, теоремы Гульдена, вычисление работы и давления
- •Несобственные интегралы: определение, признаки сравнения
- •Двойной интеграл: определение, геометрический смысл, свойства, правила вычисления, замена переменных
- •Геометрические приложения двойного интеграла: площадь плоской фигуры, объем тела, площадь поверхности
- •Физические приложения двойного интеграла: масса, статические моменты, координаты центра тяжести и моменты инерции пластины.
- •Тройной интеграл: определение, геометрический смысл, теорема существования, свойства, вычисление, теорема о среднем значении.
- •Приложения тройного интеграла: объем тела, масса, координаты центра тяжести, геометрические моменты инерции.
-
Интегрирование некоторых трансцендентных функций.
1. ![]() -
многочлен.
-
многочлен.
Интеграл можно вычислять интегрированием по частям или методом неопределенных коэффициентов, отыскивая результат в виде
![]()
где Q(x) - многочлен той же степени, что и P(x).
Имеет место результат
![]()
2. ![]() -
многочлен.
-
многочлен.
Кроме интегрирования по частям, можно пользоваться формулами:
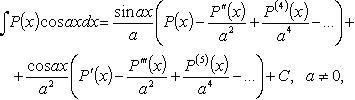

-
Интегрирование простейших иррациональных алгебраических функций.
При
интегрировании иррациональных функций
используются различные приемы. Мы
рассмотрим метод
рационализации подынтегрального
выражения. Он заключается в выборе такой
подстановки ![]() ,
которая данное подынтегральное выражение
преобразует в рациональное относительно
новой переменной
,
которая данное подынтегральное выражение
преобразует в рациональное относительно
новой переменной ![]() .
Поскольку рациональные функции мы умеем
интегрировать, такие подстановки
позволяют интегрировать и иррациональные
функции.
.
Поскольку рациональные функции мы умеем
интегрировать, такие подстановки
позволяют интегрировать и иррациональные
функции.
Пусть ![]() —
рациональная функция от
—
рациональная функция от ![]() и
и ![]() ,
т. е. функция, получаемая из
,
т. е. функция, получаемая из ![]() и
чисел с помощью конечного числа
арифметических операций (сложения,
умножения и деления).
и
чисел с помощью конечного числа
арифметических операций (сложения,
умножения и деления).
Если
заменить в ![]() переменную
переменную ![]() выражением
выражением ![]() ,
то получим функцию
,
то получим функцию 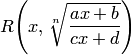 от
одной переменной
от
одной переменной ![]() .
Интеграл от нее имеет вид:
.
Интеграл от нее имеет вид:
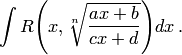
Этот интеграл рационализируется с помощью подстановки
![]() В
самом деле, так как подкоренное выражение
представляет собой дробно-линейную
относительно
В
самом деле, так как подкоренное выражение
представляет собой дробно-линейную
относительно ![]() функцию,
то переменная
функцию,
то переменная ![]() рационально
выражается через переменную
рационально
выражается через переменную ![]()
![]()
Тогда ![]() —
рациональная функция. Заменяя теперь
переменную в данном интеграле, получим
интеграл от рациональной функции новой
переменной
—
рациональная функция. Заменяя теперь
переменную в данном интеграле, получим
интеграл от рациональной функции новой
переменной ![]()
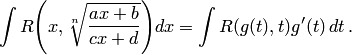
Если под знаком интеграла содержатся корни с разными показателями, но с одним и тем же дробно-линейным относительно х подкоренным выражением, то сначала следует привести их к одному показателю, после чего использовать указанный прием.
-
Интегрирование гиперболических функций
Шесть основных гиперболических функций определяются следующим образом:
|
|
|
|
|
|
|
|
|
Наиболее важные формулы дифференцирования и интегрирования гиперболических функций имеют вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приведем еще несколько полезных соотношений:
![]()
![]()
![]()
Если
подынтегральное выражение содержит
гиперболическую функцию, то такой
интеграл можно свести к интегрированию
рациональной функции с помощью
подстановки ![]() .
.
-
Интегральная сумма, определенный интеграл (определение, теорема существования, основные свойства, правила вычисления)
Пусть
на отрезке ![]() определена вещественнозначная функция
определена вещественнозначная функция ![]() .
.
Рассмотрим разбиение
отрезка ![]() —
конечное множество попарно различных
точек отрезка. Это разбиение делит
отрезок
—
конечное множество попарно различных
точек отрезка. Это разбиение делит
отрезок ![]() на n отрезков
на n отрезков ![]() .
Длина наибольшего из отрезков
.
Длина наибольшего из отрезков ![]() называется шагом
разбиения,
где
называется шагом
разбиения,
где ![]() —
длина элементарного отрезка.
—
длина элементарного отрезка.
Отметим
на каждом отрезке разбиения по
точке ![]() . Интегральной
суммой называется
выражение
. Интегральной
суммой называется
выражение ![]() .
.
Если
при стремлении шага разбиения к нулю
интегральные суммы стремятся к одному
и тому же числу, независимо от выбора ![]() ,
то это число называется интегралом функции
,
то это число называется интегралом функции ![]() на
отрезке
на
отрезке ![]() ,
то есть
,
то есть 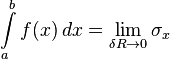 .
.
Определенным интегралом от функции f(x) на отрезке [a,b] называют предел, к которому стремится интегральная сумма.
Теорема существования определённого интеграла. Если функция f(x) непрерывна на отрезке [a,b], то она интегрируема по этому отрезку.
Свойства:
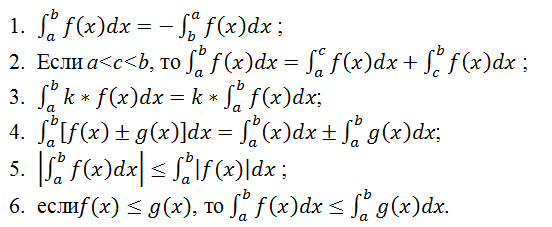
Правило. Для вычисления определенного интеграла от непрерывной функции надо найти для нее первообразную функцию и составить разность значений этой последней функции при верхнем и нижнем пределах интегрирования.

