21. Несобственные интегралы: определение, признаки сравнения

Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий.

• Область интегрирования является бесконечной. Например, является бесконечным интервалом .

• Функция f(x) не ограничена в области интегрирования.

Пусть функции f(x) и g(x) интегрируемы по любому отрезку [a,b] и при  удовлетворяют неравенствам . Тогда:

22. Двойной интеграл: определение, геометрический смысл, свойства, правила вычисления, замена переменных

Двойным интегралом называется предел двойной интегральной суммы при условии стремления к нулю диаметров всех ячеек, если он существует и не зависит он способа разбиения области D, от способа выбора ячеек C_i,j(x_i,y_j) внутри каждой ячейки

Геометрический смысл: двойной интеграл от функции f(x,y)≥0 на области S равен объему цилиндрического тела с основанием S и ограниченного сверху поверхностью z=f(x,y)

Двойной интеграл обладает следующими свойствами:

1. 

2. 

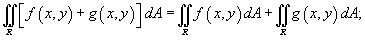
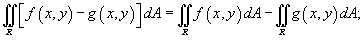
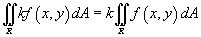3. , где k - константа;

4. Если 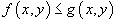 в области R, то ;

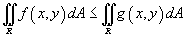5. Если f(x,y)≥0 в области R и 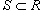, то ;

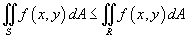6. Если f(x,y)≥0 на R и области R и S являются непересекающимися (рисунок 5), то 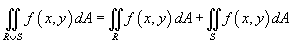.  Здесь 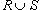 означает объединение этих двух областей.

Двойной интеграл вычисляется через повторные или двукратные интегралы. Различаются два основных вида областей интегрирования.

1)Область интегрирования S ограничена прямыми х=а, х=b и кривыми y=φ₁(x), y=φ₂(x),

Для такой области двойной интеграл вычисляется через повторный по формуле:

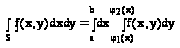
Сначала вычисляется внутренний интеграл:

При вычислении внутреннего интеграла ‘у’ считается переменной, а ‘х’-постоянной.

2)Область интегрирования S ограничена прямыми у=С, у=d и кривыми x=ψ₁(y), x=ψ₂(y)

Для такой области двойной интеграл вычисляется через повторный по формуле:

Сначала вычисляется внутренний интеграл, затем внешний.

При вычислении внутреннего интеграла ‘х’ считается переменной, а ‘у’-постоянной.

3)Если область интегрирования не относится ни к 1 ни ко второму случаю, то разбиваем ее на части таким образом, чтобы каждая из частей относилась к одному из этих двух видов.

Замена переменных в двойном интеграле описывается формулой

Итак, замена переменных в двойном интеграле производится с помощью следующих трех шагов:

1. Найти образ S в новой системе координат (u,v) для исходной области интегрирования R;

2. Вычислить якобиан преобразования (x,y)⇾(u,v) и записать дифференциал в новых переменных;

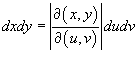3. Заменить в подынтегральном выражении исходные переменные x и y, выполнив, соответственно, подстановки x=x(u,v) и y=y(u,v) 

23. Геометрические приложения двойного интеграла: площадь плоской фигуры, объем тела, площадь поверхности

Площадь плоской фигуры

Если f (x,y) = 1 в интеграле , то двойной интеграл равен площади области интегрирования R.  Площадь области типа I (элементарной относительно оси Оy) выражается через повторный интеграл в виде

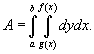
Аналогично, площадь области типа II (элементарной относительно оси Оx) описывается формулой

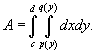
Объем тела

Если f (x,y) > 0 в области интегрирования R, то объем цилиндрического тела с основанием R, ограниченного сверху поверхностью z = f (x,y), выражается формулой

В случае, когда R является областью типа I, ограниченной линиями x=a, x=b, y=h(x), y=g(x), объем тела равен

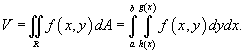
Для области R типа II, ограниченной графиками функций y=c, y=d, x=q(y), x=p(y), объем соответственно равен

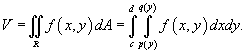
Если в области R выполняется неравенство , то объем цилиндрического тела между поверхностями z₁ = f (x,y) и z₂ = g (x,y) с основанием R равен

Площадь поверхности

Предположим, что поверхность задана функцией z = f (x,y), имеющей область определения R. Тогда площадь такой поверхности над областью z определяется формулой

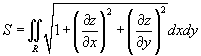
при условии, что частные производные  и  непрерывны всюду в области R. 

Площадь и объем в полярных координатах

Пусть S является областью, ограниченной линиями  (рисунок 3). Тогда площадь этой области определяется формулой

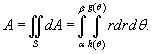
Объем тела, ограниченного сверху поверхностью  с основанием S, выражается в полярных координатах в виде