
- •Глава III. Дифференциальное исчисление функций нескольких переменных
- •3.1. Определение функции нескольких переменных
- •3.2. Предел функции нескольких переменных
- •3.3. Бесконечно малые функции нескольких переменных
- •3.4. Свойства пределов
- •3.5. Непрерывность функций нескольких переменных. Точки и линии разрыва
- •Свойства непрерывных функций
- •3.6. Частные приращения и частные производные функции нескольких переменных
- •3.9. Достаточные условия дифференцируемости функции нескольких переменных
- •3.10. Полный дифференциал функции нескольких переменных
- •3.10. 1. Применение полного дифференциала функции нескольких переменных для приближенных вычислений
- •3.11. Частные производные высших порядков
- •3.12. Дифференциалы высших порядков
- •3.13. Частные производные сложной функции нескольких переменных
- •3.14. Производная функции, заданной неявно
- •3.15. Производная функции по направлению
- •3.16. Градиент функции, его свойства
- •3.17. Формула Тейлора для функций двух переменных
- •3.18. Локальный экстремум функции нескольких переменных
- •3.19. Необходимый признак локального экстремума
- •3.20. Достаточный признак локального экстремума функции двух переменных
- •3.21. Метод наименьших квадратов (мнк)
- •3.22. Условный экстремум функции нескольких переменных
- •3.22.1. Постановка задачи
- •3.22.2. Нахождение критических точек
- •3.22.3. Метод множителей Лагранжа
- •3.22.4. Достаточный признак условного экстремума функции двух переменных
- •3.23. Абсолютный экстремум функций нескольких переменных
- •Вопросы к экзамену Введение в математический анализ
- •Дифференциальное исчисление функций одной переменной
- •Дифференциальное исчисление функций нескольких переменных
- •Литература Основная литература
- •Дополнительная литература
- •Шершнев Владимир Григорьевич математический анализ
- •Часть I. Дифференциальное исчисление
- •117997, Москва, Стремянный пер. 36.
3.15. Производная функции по направлению
Пусть функция
![]() непрерывная и дифференцируемая, вектор
непрерывная и дифференцируемая, вектор
![]() задает направление. Пусть имеется точка
задает направление. Пусть имеется точка
![]() и в направлении
и в направлении
![]() от нее точка
от нее точка
![]() (рис. 48).
(рис. 48).
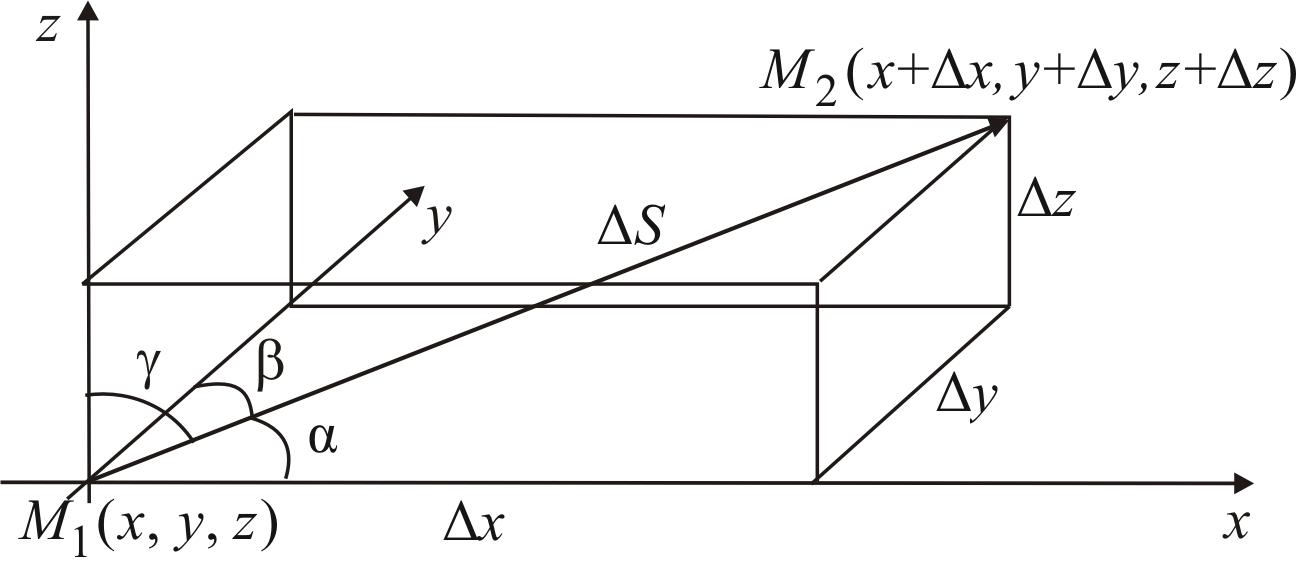
Рис. 48
Вектор
![]() имеет координаты
имеет координаты
![]() ,
,
![]() ,
,
![]() ,
т. е.
,
т. е.
![]() .
.
Модуль вектора
![]() ,
,
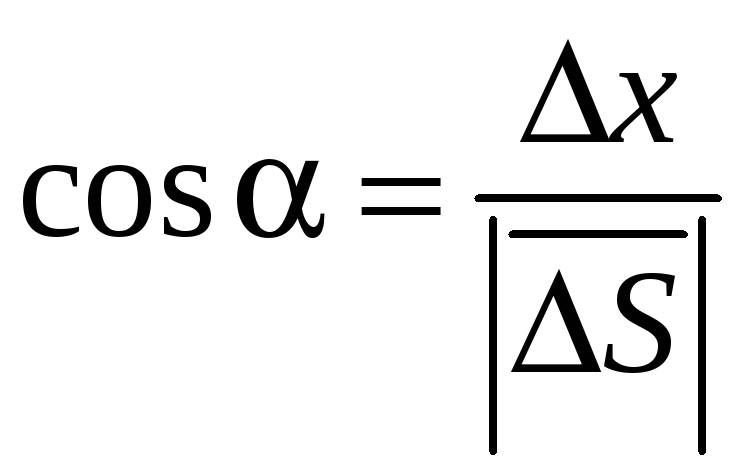 ,
,
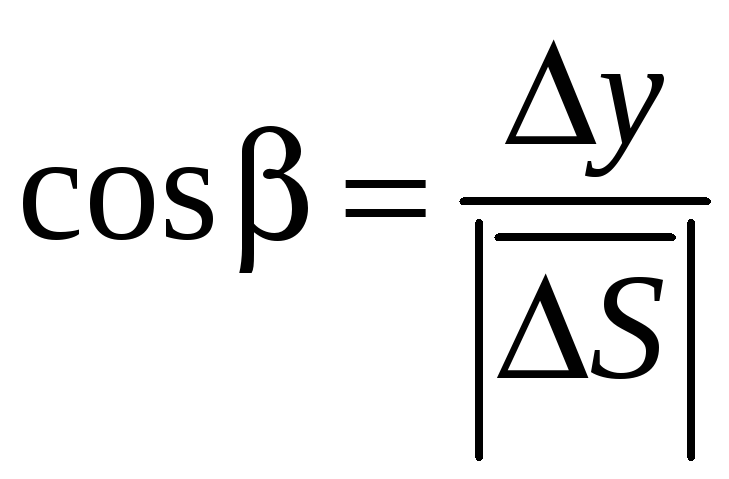 ,
,
 .
.
Косинусы cos,
cos,
cos
называются направляющими косинусами
вектора
![]() .
Если вектор
.
Если вектор
![]() единичный
единичный
![]() ,
то
,
то
![]() и его координатами являются направляющие
косинусы, т. е.
и его координатами являются направляющие
косинусы, т. е.
![]() .
.
Производной функции
![]() по направлению вектора
по направлению вектора
![]() в точке
в точке
![]() называется предел отношения приращения
функции в этом направлении к приращению
длины (модуля)
называется предел отношения приращения
функции в этом направлении к приращению
длины (модуля)
![]() вектора
вектора
![]() ,
при
,
при
![]() стремящемся к нулю
стремящемся к нулю
![]() ,
т. е.
,
т. е.
![]() .
.
Находим
![]()
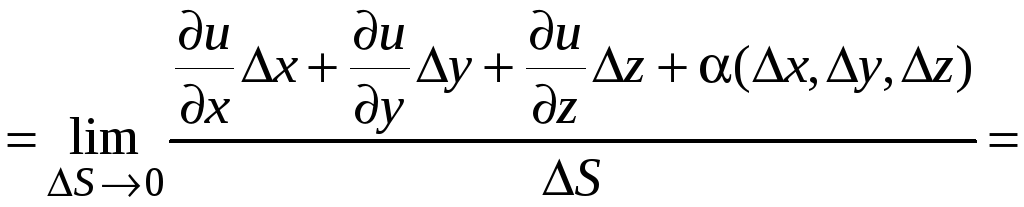
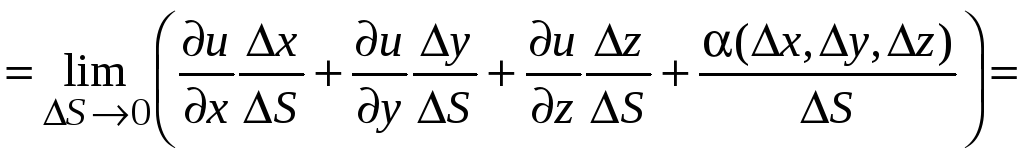
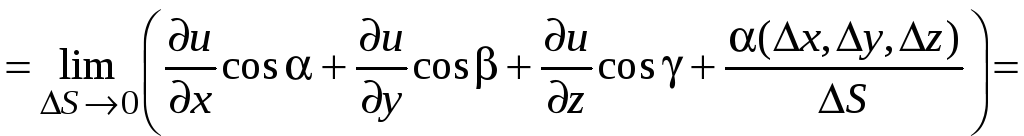
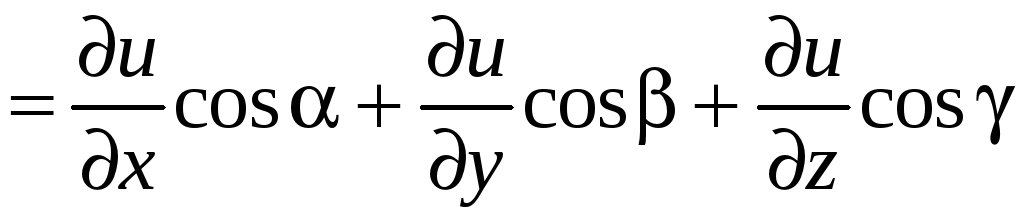 .
.
Таким образом, получена формула дифференцирования функции по направлению вектора
 .
.
Пример 3.21.
Вычислить производную функции
![]() в точке
в точке
![]() по направлению вектора
по направлению вектора
![]() .
.
Находим
![]() ,
,
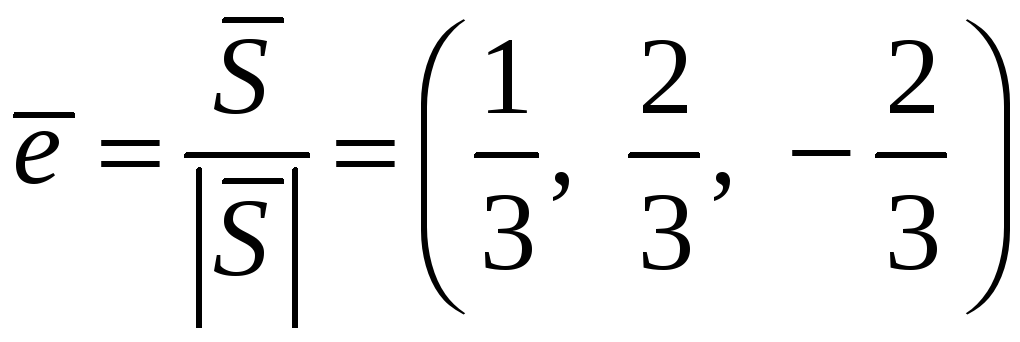 .
.
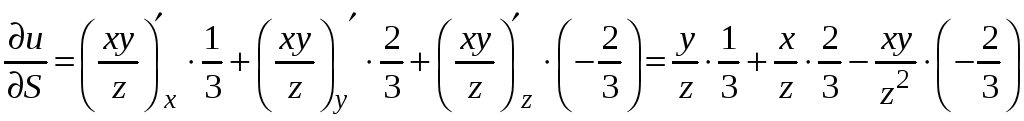 .
.
 .
.
3.16. Градиент функции, его свойства
Градиентом функции
![]() называется вектор
называется вектор
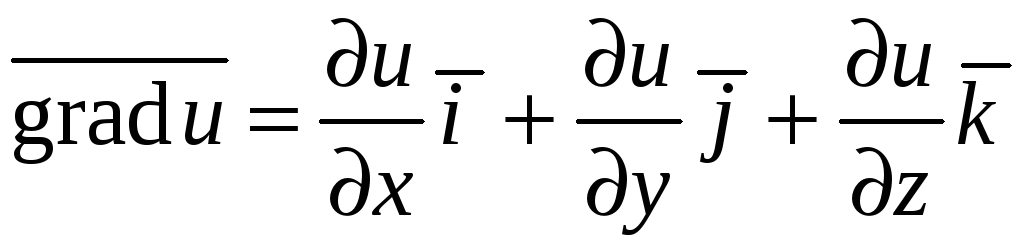 ,
,
где
![]()
единичные векторы координатного базиса
в прямоугольной декартовой системе
координат.
единичные векторы координатного базиса
в прямоугольной декартовой системе
координат.
Кратко можно
записать
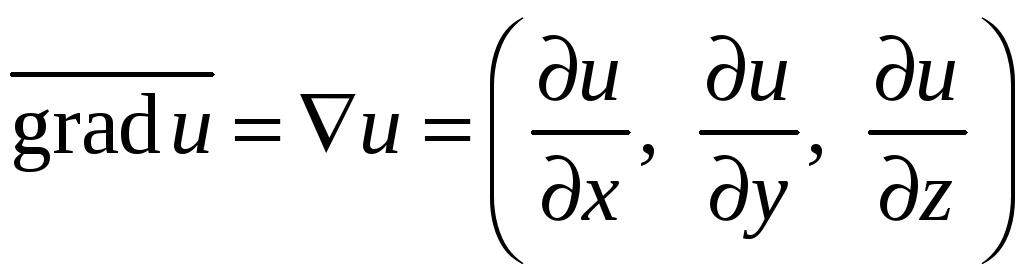 .
Здесь
знак набла.
.
Здесь
знак набла.
Пример 3.22.
Найти градиент функции
![]() в точке
в точке
![]() .
.
![]() .
.
![]() .
.
Теорема 3.5.
Производная функции
![]() по направлению вектора
по направлению вектора
![]() равняется проекции градиента этой
функции на это направление, т. е.
равняется проекции градиента этой
функции на это направление, т. е.
![]() .
.
Известно, что
проекция некоторого вектора
![]() на направление вектора
на направление вектора
![]() равняется
равняется
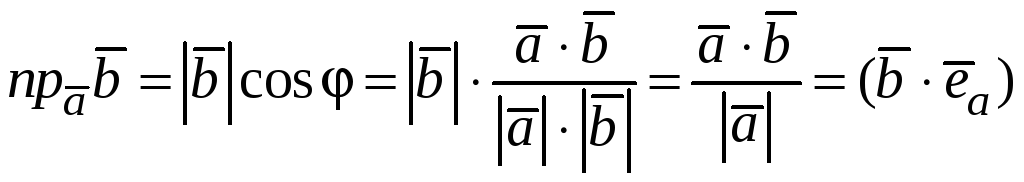 .
.
Здесь
угол между векторами
![]() и
и
![]() ,
,
![]()
скалярное произведение векторов,
скалярное произведение векторов,
![]()
единичный вектор, совпадающий по
направлению с вектором
единичный вектор, совпадающий по
направлению с вектором
![]() .
.
Найдем
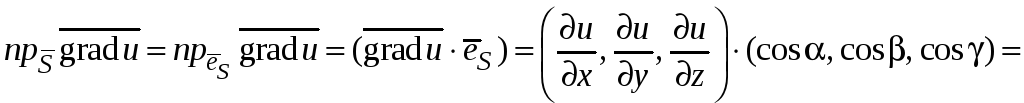
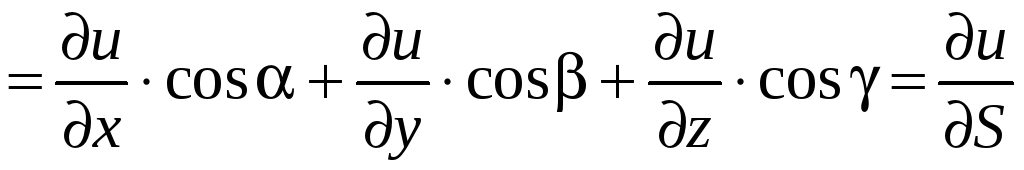 .
.
Свойство 1.
Производная функции
![]() по направлению вектора
по направлению вектора
![]() достигает своего наибольшего значения,
если направление вектора
достигает своего наибольшего значения,
если направление вектора
![]() совпадает с направлением градиента
этой функции.
совпадает с направлением градиента
этой функции.
Действительно,
производную данной функции по направлению
вектора
![]() можно записать следующим образом
можно записать следующим образом
![]() ,
где
угол между градиентом и вектором
,
где
угол между градиентом и вектором
![]() .
Если этот угол равен нулю
= 0 , то косинус этого угла и производная
функции принимают наибольшие значения,
cos0
= 1,
.
Если этот угол равен нулю
= 0 , то косинус этого угла и производная
функции принимают наибольшие значения,
cos0
= 1,
![]() .
.
Свойство 2.
Производная функции
![]() по направлению вектора
по направлению вектора
![]() равняется нулю, если направление вектора
равняется нулю, если направление вектора
![]() перпендикулярно направлению градиента
этой функции.
перпендикулярно направлению градиента
этой функции.
Действительно,
![]() .
.
Данные свойства используются при решении задач оптимизации (нахождения наибольшего, наименьшего значений функций) с помощью численных методов. Градиент функции определяет направление наибольшего изменения функции. Направление перпендикулярное градиенту определяет направление, в котором функция не изменяется.
Известно, что на
поверхности уровня
![]() функция
функция
![]() не изменяется. Следовательно, градиент
функции перпендикулярен поверхности
уровня. Это обстоятельство можно
использовать для написания уравнения
касательной плоскости к поверхности
не изменяется. Следовательно, градиент
функции перпендикулярен поверхности
уровня. Это обстоятельство можно
использовать для написания уравнения
касательной плоскости к поверхности
![]() .
Пусть точка
.
Пусть точка
![]() принадлежит поверхности. Найдем градиент
функции
принадлежит поверхности. Найдем градиент
функции
![]() в этой точке
в этой точке
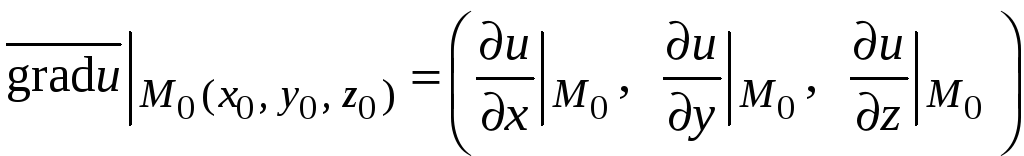 и напишем уравнение плоскости, проходящей
через точку
и напишем уравнение плоскости, проходящей
через точку
![]() перпендикулярно вектору
перпендикулярно вектору
![]() .
Получаем уравнение касательной плоскости
.
Получаем уравнение касательной плоскости
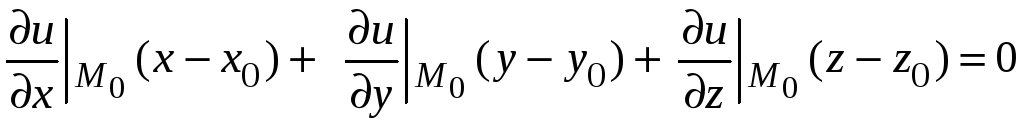 .
.
Пример 3.23. Написать уравнение касательной плоскости к эллипсоиду
![]() в точке
в точке
![]() .
.
Находим
![]() ,
,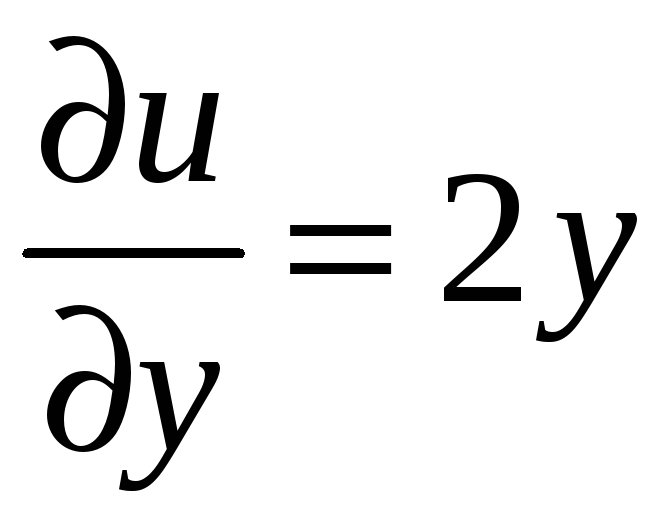 ,
,
![]() ;
;
![]() ,
,
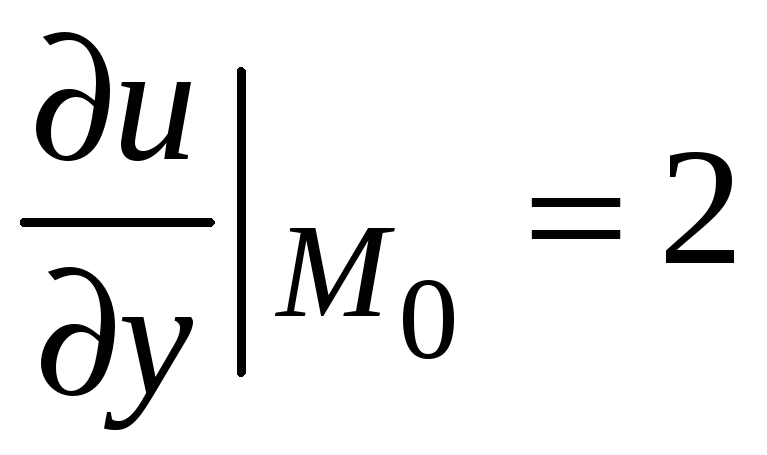 ,
,
![]() .
.
Записываем уравнение касательной плоскости
![]()
![]() .
.
