3.22. Условный экстремум функции нескольких переменных

3.22.1. Постановка задачи

Требуется найти экстремум функции при условии, что переменные x и y удовлетворяют уравнению .

Геометрически это можно представить следующим образом (рис. 53).

Рис. 53

Требуется найти точку на поверхности , имеющую наибольшую аппликату (z) при условии, что точка находится на некоторой кривой, расположенной на этой поверхности над кривой в плоскости Oxy.

3.22.2. Нахождение критических точек

Будем считать, что уравнение задает неявно функцию . Подставим эту функцию в функцию , получим функцию одной переменной . Для нахождения экстремума этой функции используем необходимый признак. Найдем критические точки, в которых производная равна нулю

.

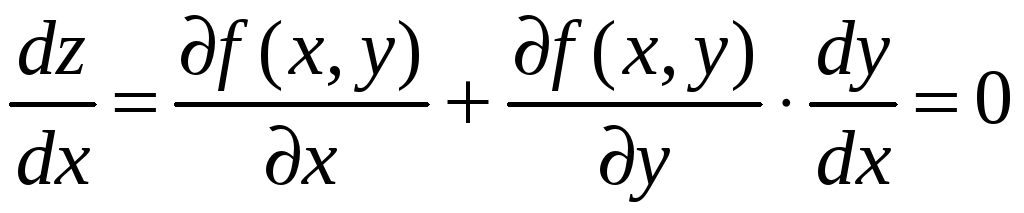Также подставим в уравнение и продифференцируем по х

.

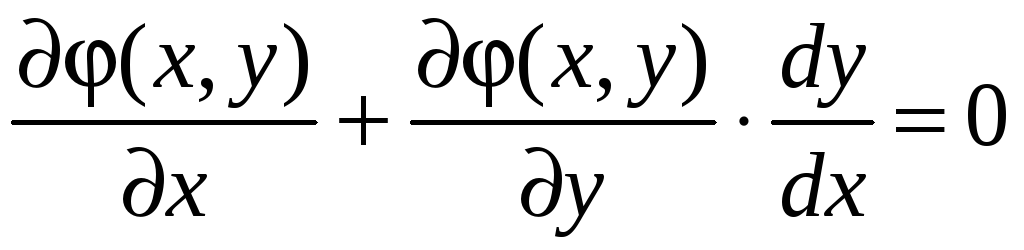Решим систему

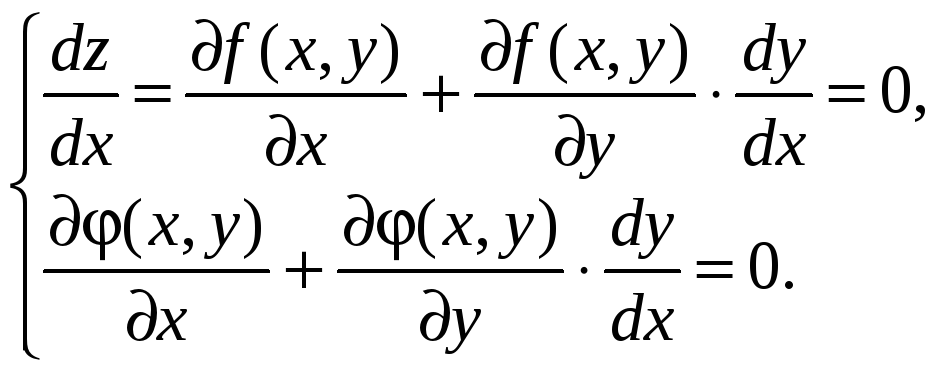
Второе равенство умножим на некоторый множитель  и прибавим к первому. Получим

Будем считать, что 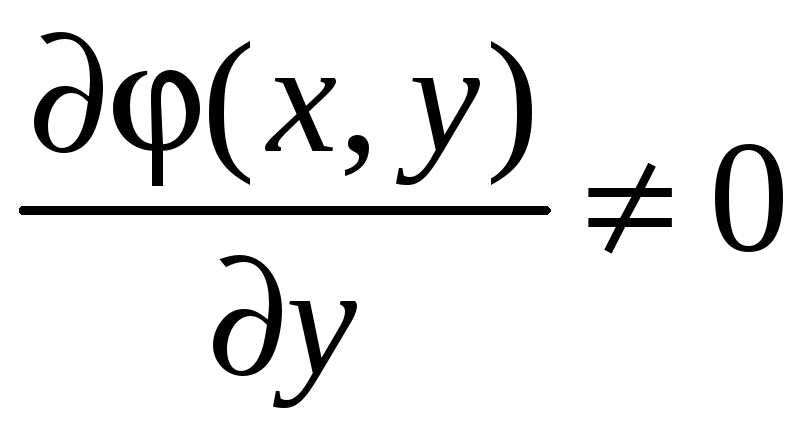. Тогда множитель  можно подобрать так, чтобы 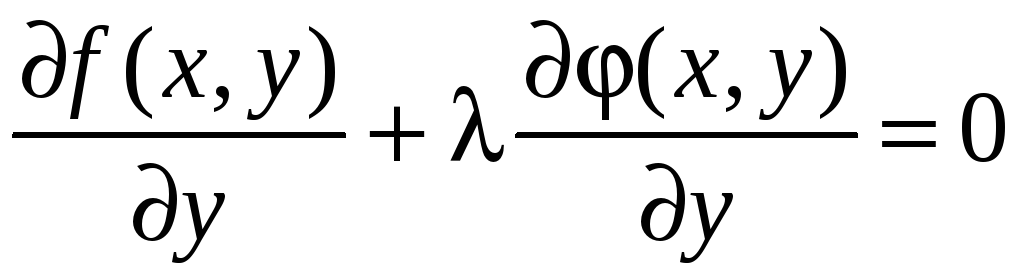. В этом случае уравнение

распадется на два уравнения. Получится система

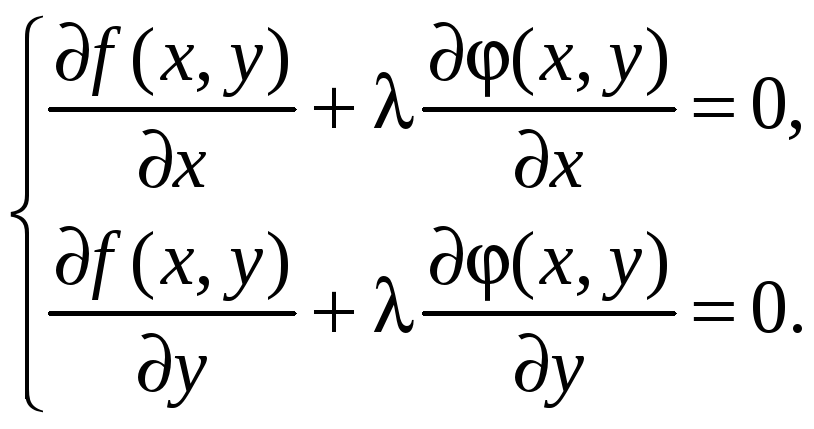
Эти два уравнения совместно с уравнением образуют систему уравнений для нахождения критических точек

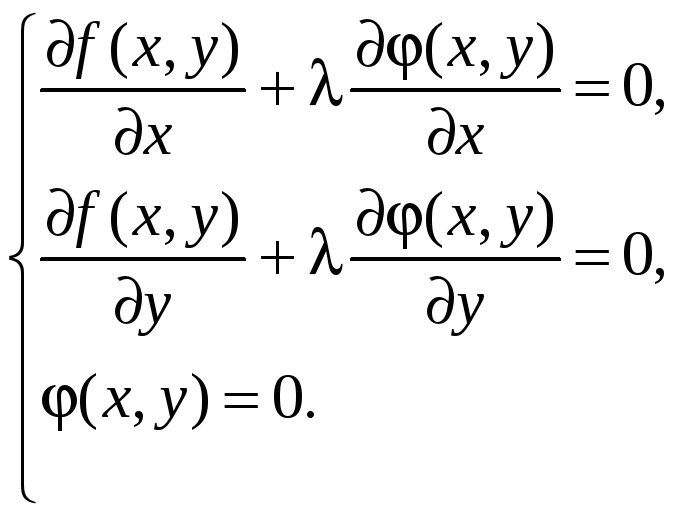
Критические точки, найденные при решении этой системы, необходимо проверить на наличие в них экстремума с помощью достаточного признака.

3.22.3. Метод множителей Лагранжа

Нетрудно заметить, что левые части уравнений системы для нахождения критических точек являются частными производными функции вида

.

Составленная таким образом функция называется функцией Лагранжа, а множитель  называется множителем Лагранжа.

Систему для нахождения критических точек с помощью функции Лагранжа можно записать в виде

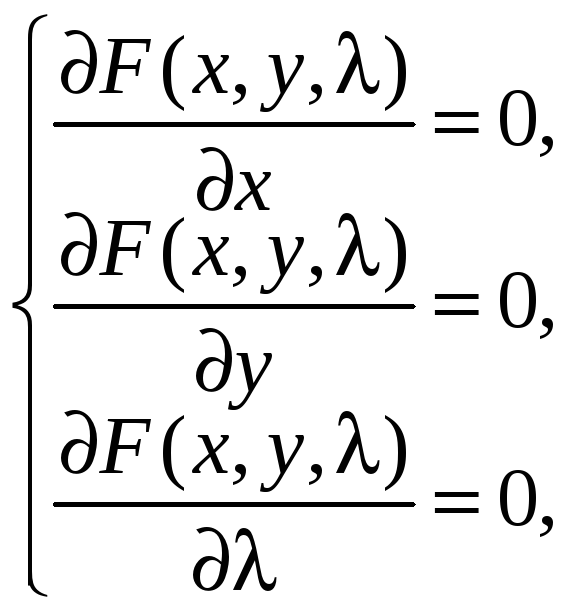
В случае n переменных задача на условный экстремум формулируется следующим образом.

Найти экстремум функции , если независимые переменные удовлетворяют системе ограничений

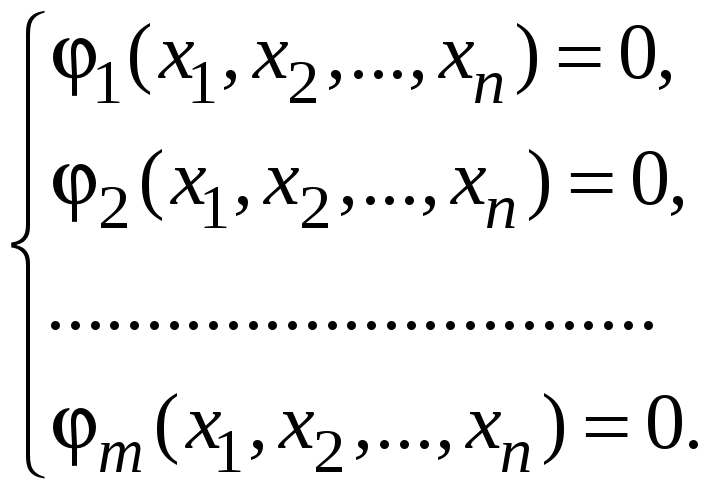
В этом случае функция Лагранжа имеет вид

.

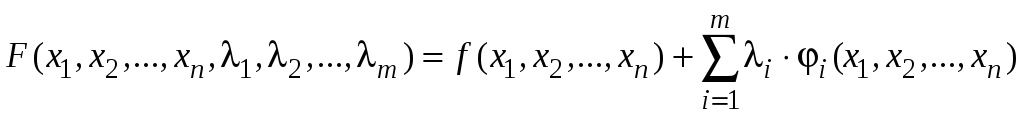Данную функцию исследуют на обычный безусловный экстремум.

Система для нахождения критических точек имеет вид

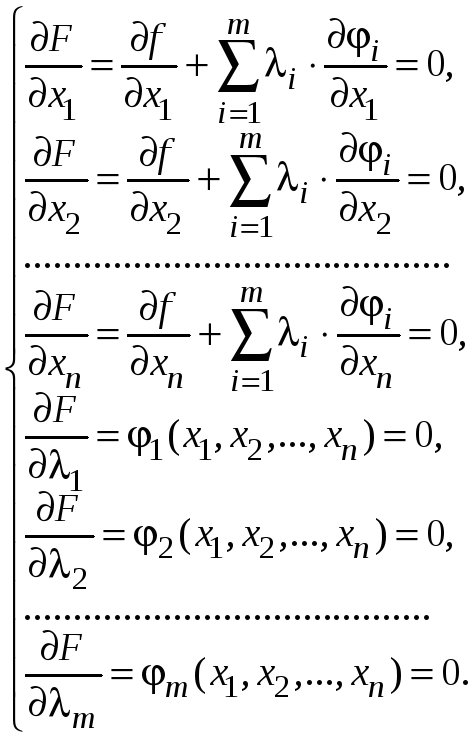
или в более компактной записи

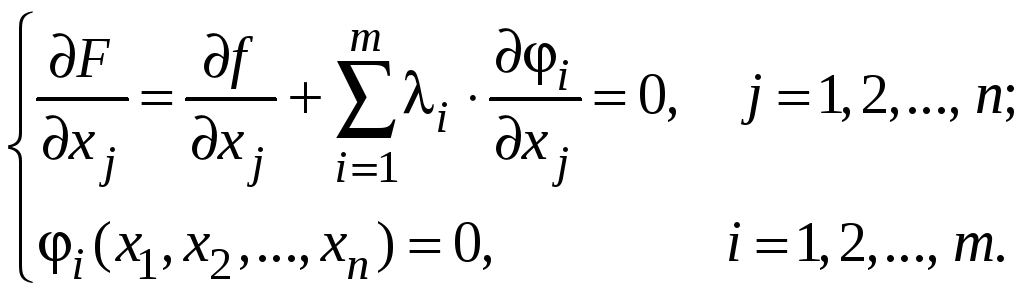
В результате решения данной системы с n + m переменными могут быть найдены критические точки .

3.22.4. Достаточный признак условного экстремума функции двух переменных

Пусть решается задача на условный экстремум

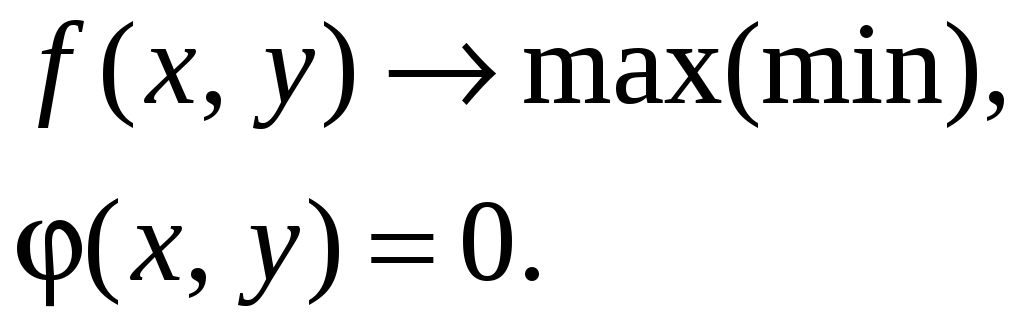
Запишем функцию Лагранжа

.

Составим систему для нахождения критических точек

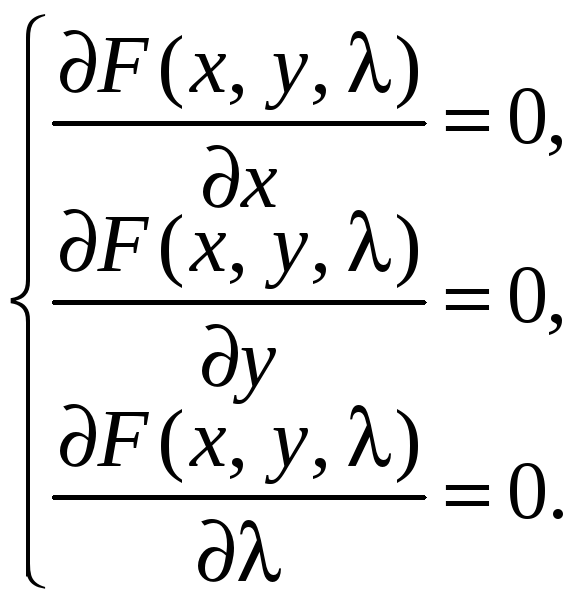
Пусть в результате решения этой системы найдена критическая точка . Тогда в этой точке равны нулю частные производные

,

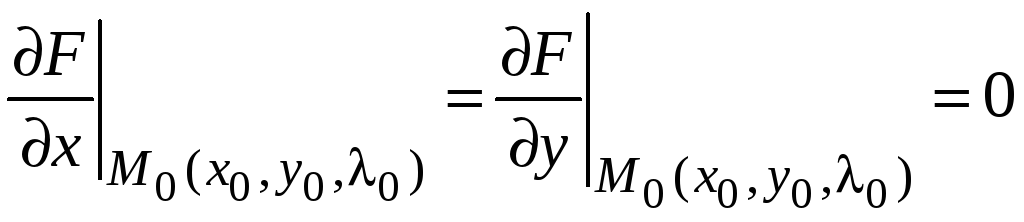следовательно, и дифференциал первого порядка .

Наличие экстремума функции в точке определяется по тому, что является или нет знакоопределенной функцией приращение функции в окрестности этой точки. Ввиду того, что дифференциал первого порядка в этой точке равен нулю, в первом приближении . Если в критической точке , то и точка является точкой минимума. Если же , и точка является точкой максимума.

Дифференциал второго порядка функции трех переменных является квадратичной формой относительно .

.

В матричной записи этот дифференциал имеет вид

.

Данную квадратичную форму можно исследовать на знакоопределееность с помощью критерия Сильвестра.

Согласно данному критерию, для того чтобы квадратичная форма была знакоположительной в некоторой -окрестности точки , т.е. , должны быть положительными все три главных минора матрицы этой формы.

, , .

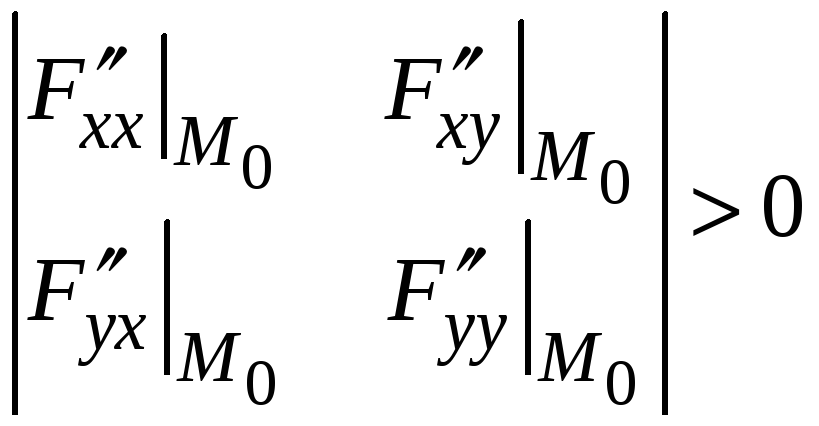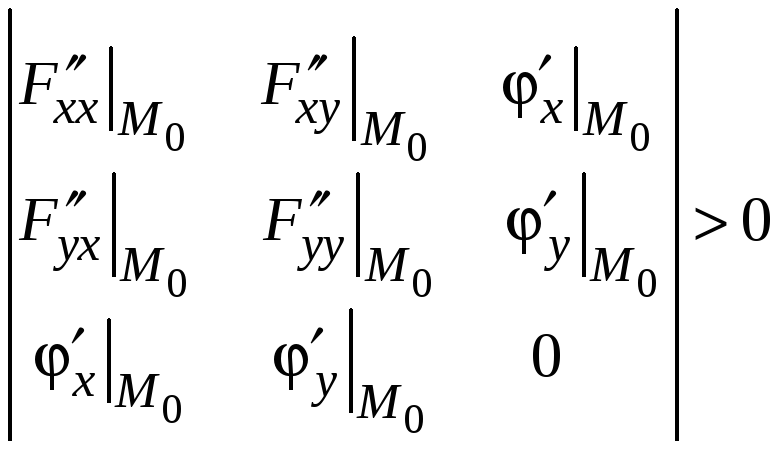В этом случае функция будет иметь минимум в точке .

Для того чтобы квадратичная форма была знакоотрицательной в некоторой -окрестности точки , т.е. , должны быть отрицательными первый и третий главные минора матрицы, а второй минор  положительный.

. , .

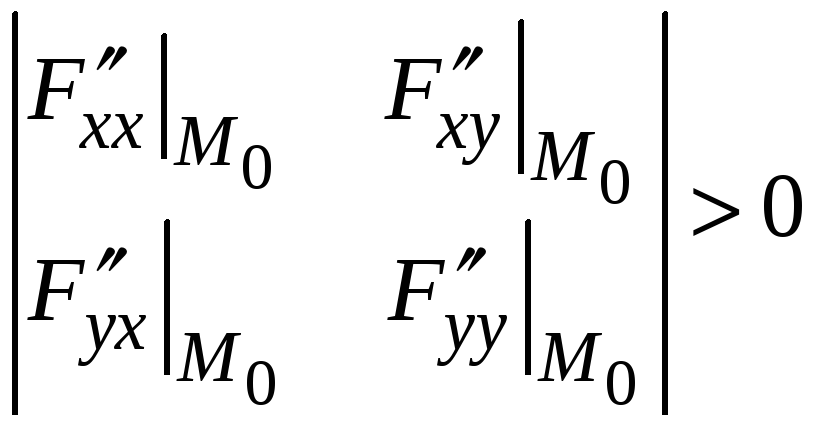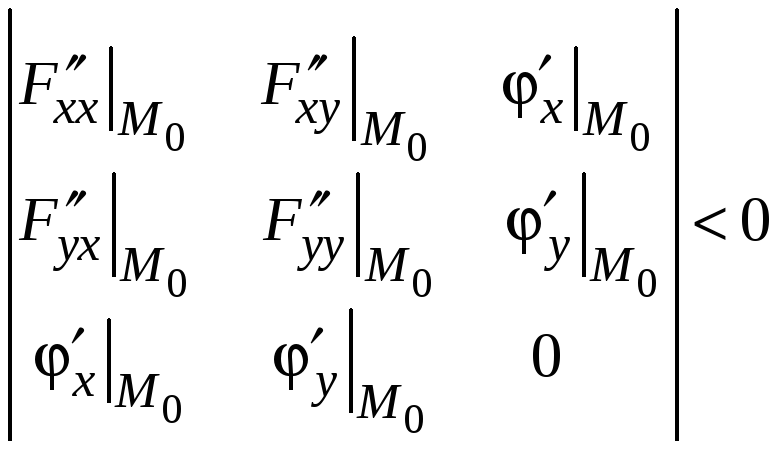В этом случае функция будет иметь максимум в точке .

В более удобном виде достаточный признак на условный экстремум функции двух переменных в критической точке записывают в виде одного определителя

.

Если  > 0, то  точка минимума, если  < 0, то  точка максимума.

Пример 3.27. Найти наибольший объем и длину ребер прямоугольного параллелепипеда, если его полная поверхность равна 2а.

Обозначим длины ребер параллелепипеда через x, y, z. Тогда его объем , а полная поверхность равняется . Поделим это равенство на 2, получим уравнение, которое является ограничением при нахождении максимального объема параллелепипеда. Таким образом, задача формулируется следующим образом.

Найти максимум функции

при условии, что ее переменные удовлетворяют уравнению

.

Запишем функцию Лагранжа

.

Составим систему уравнений для нахождения критических точек.

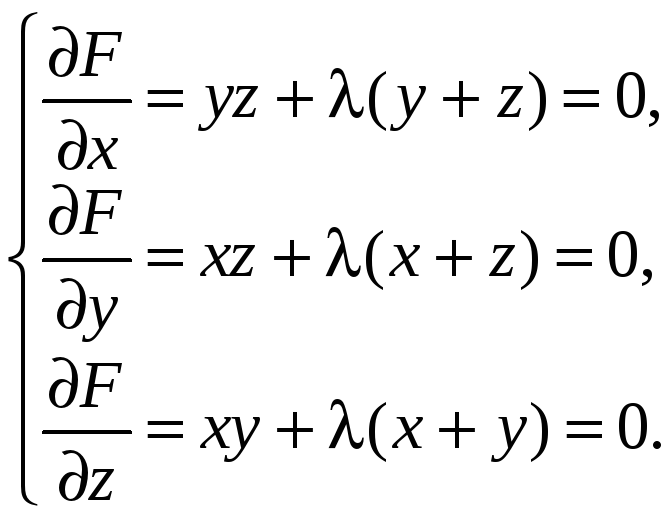
Умножим первое уравнение на х, второе на y, а третье на z и сложим, получим

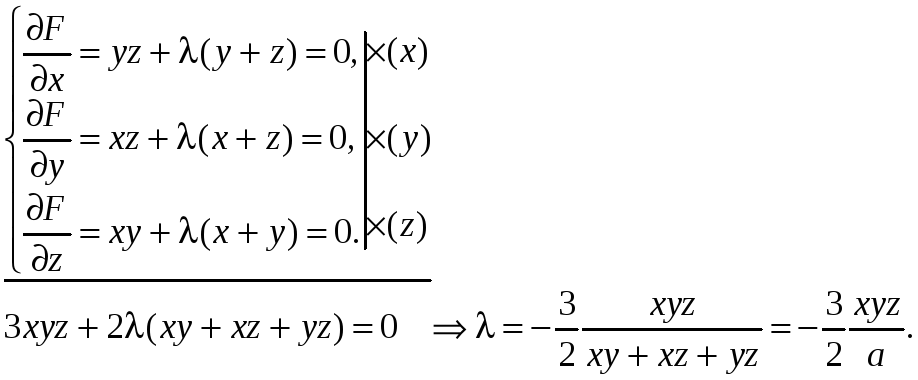
Подставим это значение  в систему уравнений и поделим первое уравнение на yz, второе на xz, а третье на xy.

.

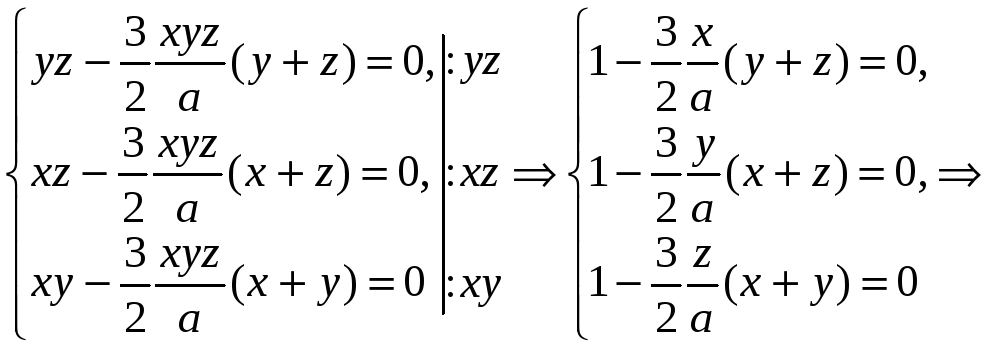
Отсюда получаем

,

,

.

Из равенства получаем .

Так как все ребра параллелепипеда равны , то объем .

Пример 3.28. Найти условные экстремумы функции при 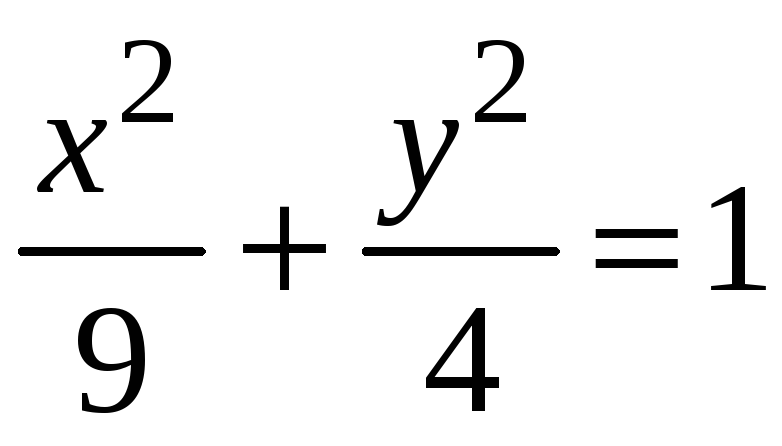(Рис. 54).

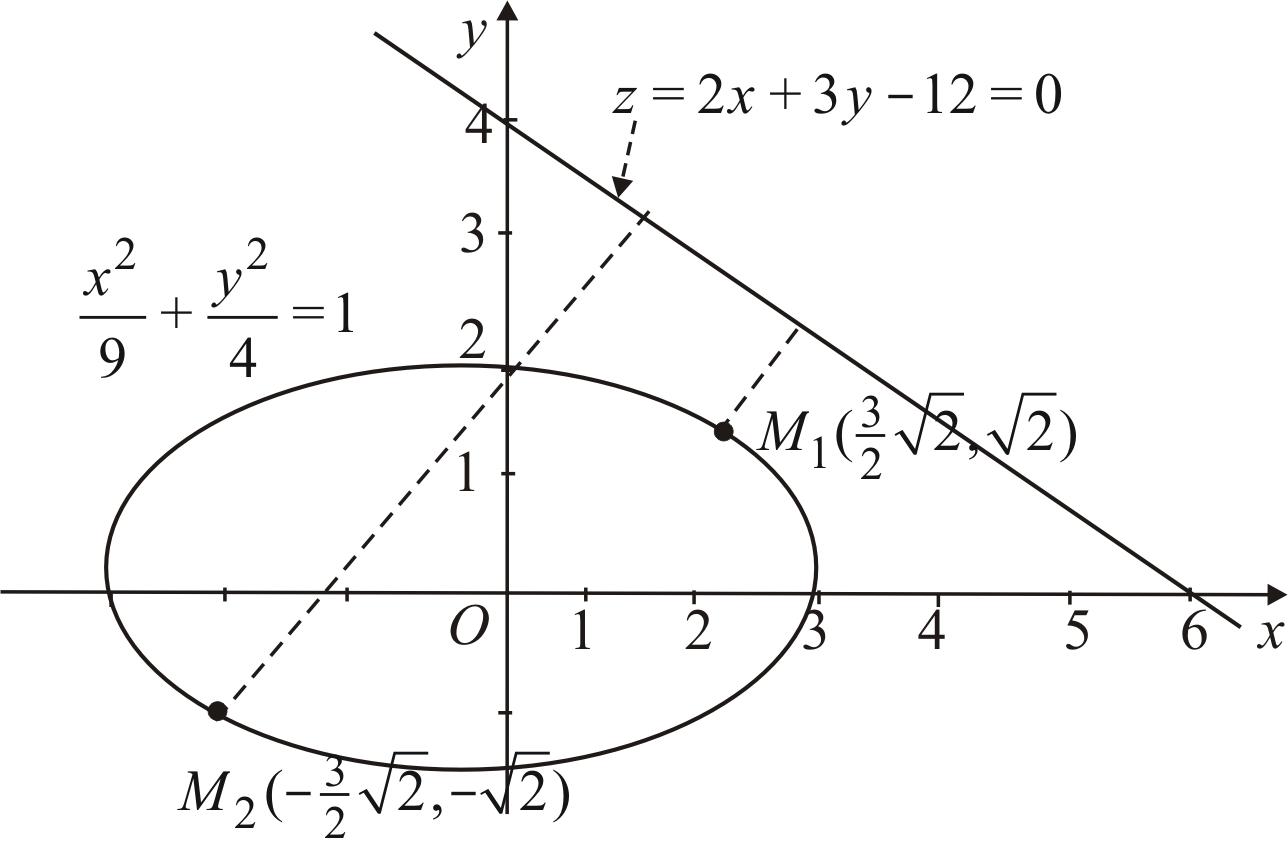
Рис. 54

Запишем функцию Лагранжа

.

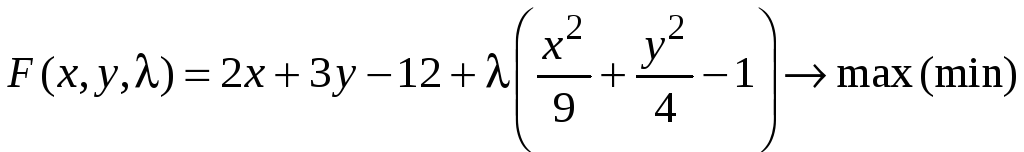Составим систему для нахождения критических точек

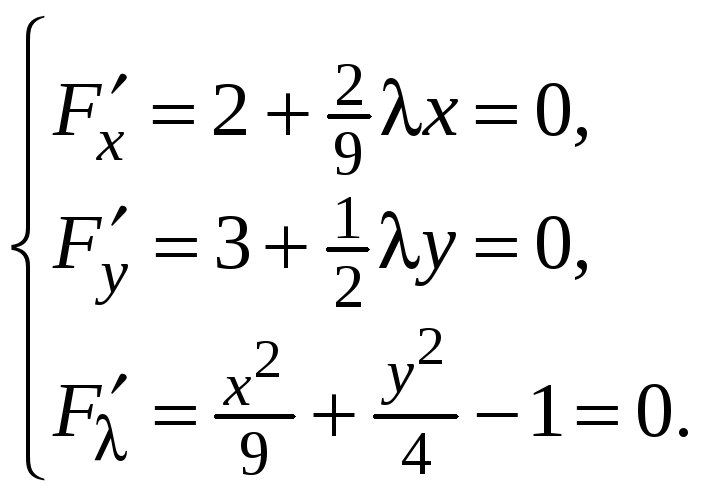
Из первого и второго уравнений найдем .

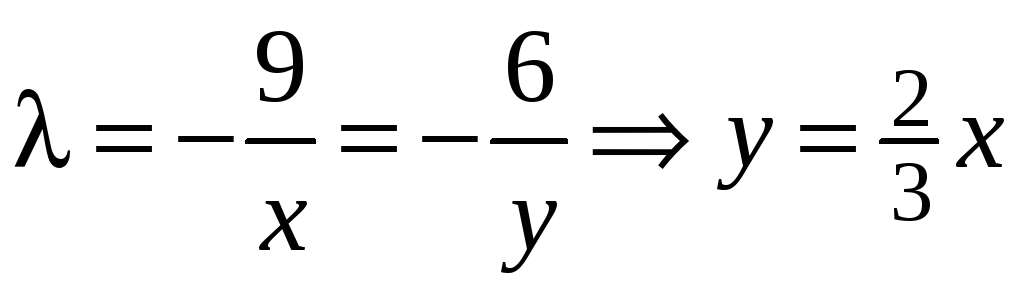Из третьего уравнения получим .

Тогда , .

Критические точки , исследуем на экстремум по достаточному признаку.

Найдем частные производные второго порядка: , , , , , .

Вычисляем значения этих производных в критической точке и составляем определитель .

, , ,

, , .

.

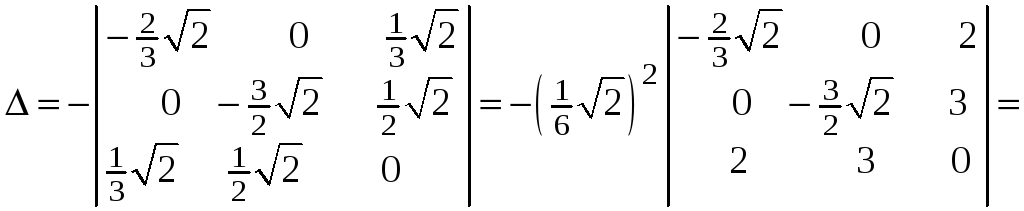
Следовательно, в точке функция имеет локальный максимум. Вычисляем значение функции в этой точке

.

Вычисляем значения производных функции в критической точке и составляем определитель .

, , ,

, , .

.

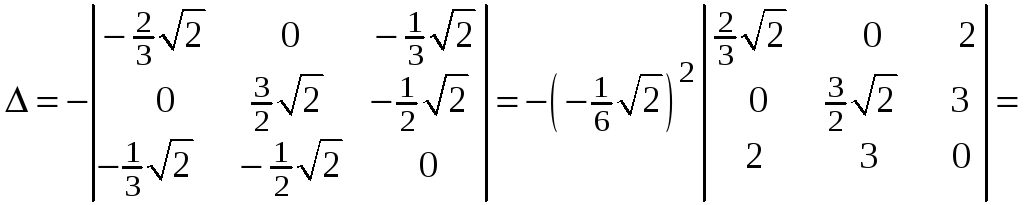
Следовательно, в точке функция имеет локальный минимум. .

О т в е т. в точке ;

в точке .