
- •Глава 8. Числовые ряды
- •8.1. Основные понятия
- •8.1. 1. Определение числового ряда
- •8.1.2. Сходимость числового ряда. Сумма ряда
- •8.1.3. Свойства сходящихся рядов
- •8.2. Необходимый признак сходимости числового ряда
- •8.4.2. Признак Даламбера сходимости знакоположительных рядов
- •8.4.3. Радикальный признак Коши сходимости числового ряда
- •8.4.4. Интегральный признак Коши
- •8.5. Знакочередующиеся ряды. Теорема Лейбница
- •8.6. Знакопеременные ряды. Теорема об абсолютной сходимости числового ряда
- •Глава 9. Степенные ряды
- •9.1. Функциональные ряды. Общие понятия
- •9.2. Равномерная сходимость функциональных рядов. Теорема Вейерштрасса
- •9.3. Теорема Абеля о виде области сходимости степенного ряда
- •9.4. Радиус и область сходимости степенного ряда
- •9.5. Ряды Тейлора и Маклорена
- •9.6. Разложение в ряд Маклорена основных элементарных функций
- •9.7. Применение рядов для приближенных вычислений
- •Вопросы к экзамену Неопределённый интеграл
- •Определённый интеграл
- •77. Дифференцирование интегралов, зависящих от параметра. Формула Лейбница. Гамма-функция. Дифференциальные уравнения
- •Шершнев Владимир Григорьевич математический анализ
- •Часть 2. Интегральное исчисление
- •117997, Москва, Стремянный пер. 36.
8.1.3. Свойства сходящихся рядов
1. Сходимость
числового ряда
![]() не нарушится, если все его члены умножить
на некоторое отличное от нуля число ;
причем
не нарушится, если все его члены умножить
на некоторое отличное от нуля число ;
причем
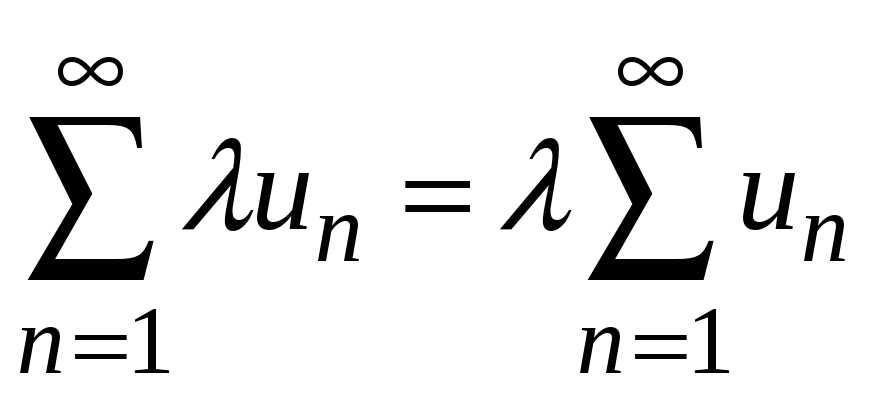 .
.
Д о к а з а т е л ь с т в о. Используем определение суммы ряда и свойства пределов, получаем
 .
.
2. При сложении
соответствующих членов двух сходящихся
рядов
![]() и
и
![]() получится сходящийся ряд; причем
получится сходящийся ряд; причем
 .
.
Д о к а з а т е л ь с т в о. Используем определение суммы ряда и свойства пределов, получаем
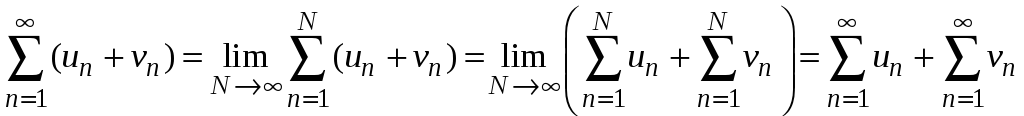 .
.
3. Сходимость ряда не нарушится, если отбросить конечное число его членов.
Д о к а з а т е л ь
с т в о. Пусть сумма ряда
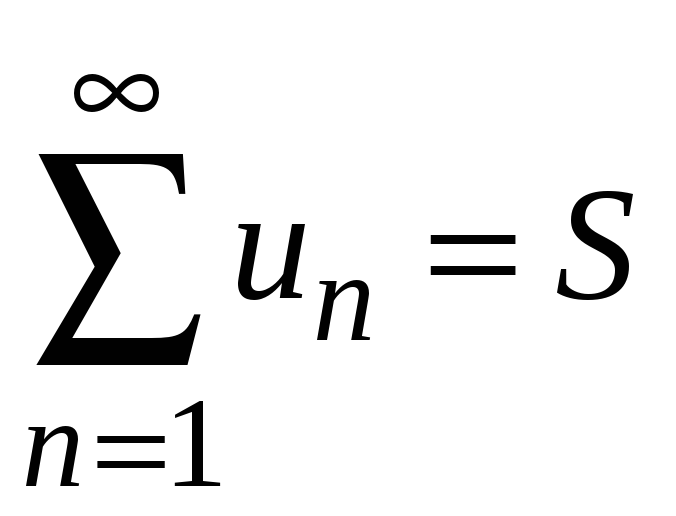 .
Не нарушая общности можно считать, что
отбрасываются k
первых его членов, сумма которых
.
Не нарушая общности можно считать, что
отбрасываются k
первых его членов, сумма которых
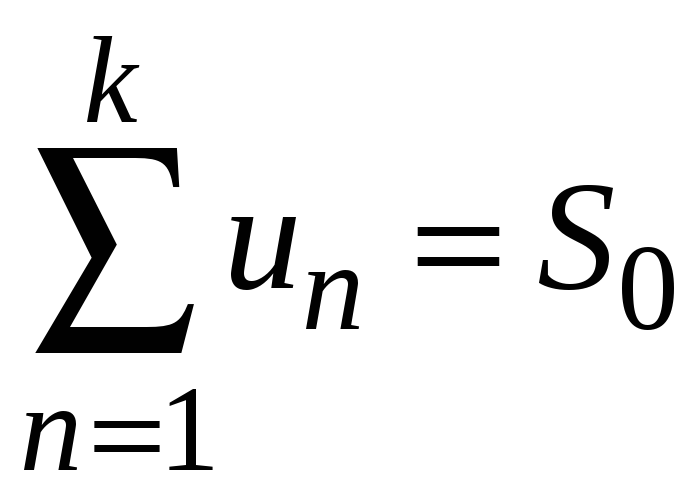 .
Так как ряд сходящийся, то
.
Так как ряд сходящийся, то
![]() являются конечными величинами, поэтому
являются конечными величинами, поэтому
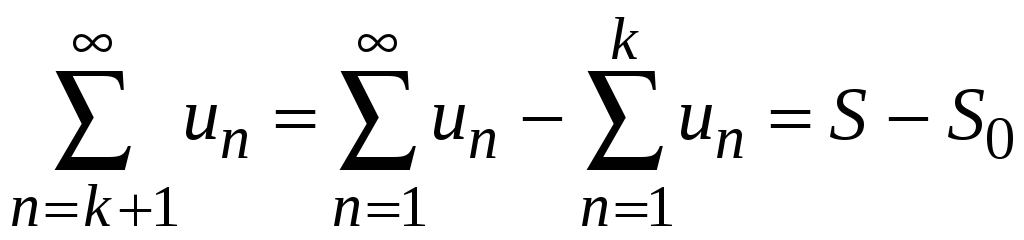 так же является конечной величиной и,
следовательно, ряд
так же является конечной величиной и,
следовательно, ряд
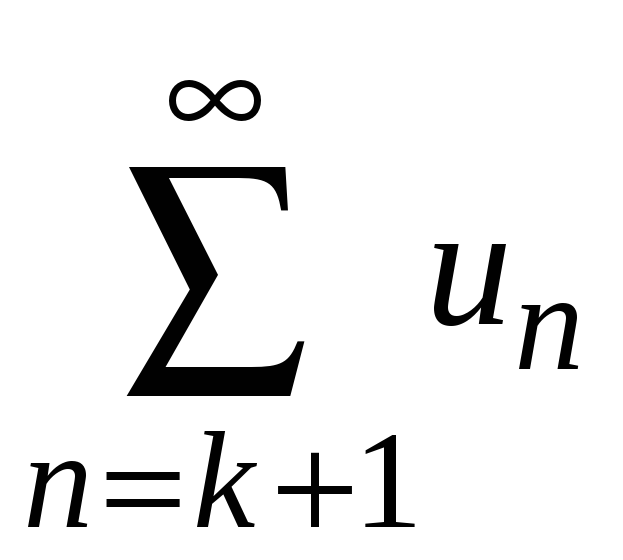 сходится.
сходится.
Отсюда также следует, что если в расходящемся ряде отбросить конечное число членов, то ряд останется расходящимся.
8.2. Необходимый признак сходимости числового ряда
Теорема 8.1.
Если числовой ряд
![]() сходится,
то его общий член
сходится,
то его общий член
![]() при неограниченном возрастании его
номера стремится к нулю, т. е.
при неограниченном возрастании его
номера стремится к нулю, т. е.
![]() .
.
Д о к а з а т е л ь
с т в о. Представим общий член
![]() как разность частичных сумм и найдем
предел
как разность частичных сумм и найдем
предел
![]() .
.
Следствие.
Если предел общего члена ряда при
неограниченном возрастании его номера
отличен от нуля, т. е.
![]() ,
то ряд расходится.
,
то ряд расходится.
Пример 8.2.
Используя следствие из необходимого
признака сходимости показать, что ряд
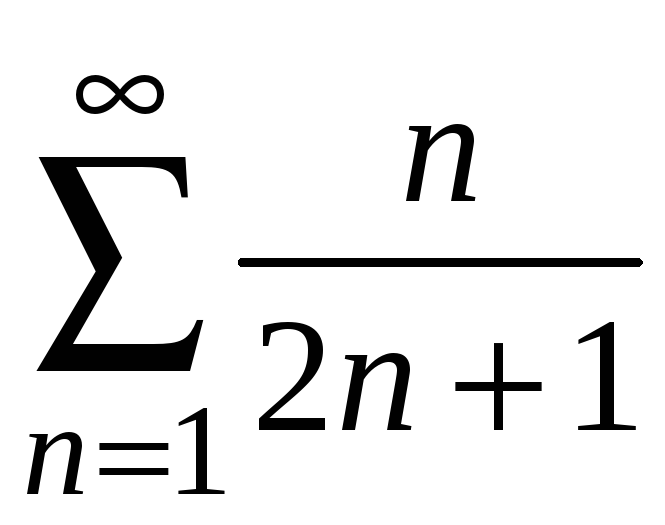 расходится.
расходится.
Находим
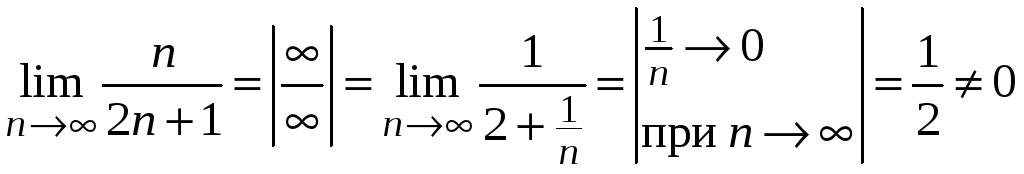 .
.
Следовательно, ряд расходится.
Данный необходимый признак сходимости числовых рядов не позволяет установить сходимость ряда. Он позволяет только установить, что ряд расходится, и только для тех рядов, которые расходятся достаточно быстро.
Пример 8.3.
Рассмотрим ряд
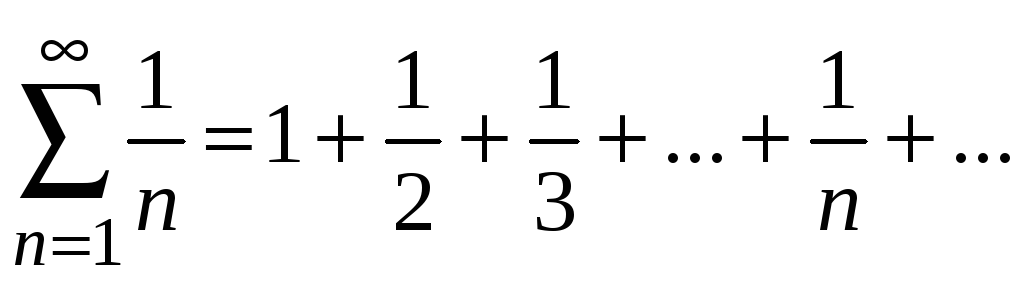 .
Данный ряд часто используется при
исследовании сходимости числовых рядов
и имеет специальное название
«гармонический».
Для данного ряда выполняется необходимый
признак, так как
.
Данный ряд часто используется при
исследовании сходимости числовых рядов
и имеет специальное название
«гармонический».
Для данного ряда выполняется необходимый
признак, так как
![]() .
Однако данный ряд расходится. Покажем
это.
.
Однако данный ряд расходится. Покажем
это.
Так как ряд имеет
бесконечное число членов, то из его
членов можно сформировать бесконечное
число групп (сумм), сумма каждой из
которых больше 1/2. Группы членов ряда
заключены в скобки. В первую группу
входит 2 члена, во вторую
![]() ,
в третью
,
в третью
![]() и т. д.
и т. д.
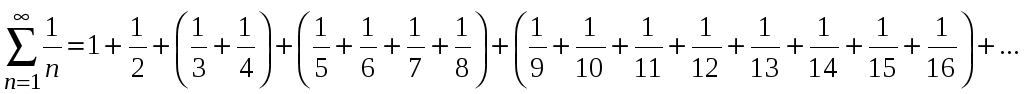 В
каждой группе заменим все слагаемые
последними, которые является наименьшими
в группах, получим неравенство
В
каждой группе заменим все слагаемые
последними, которые является наименьшими
в группах, получим неравенство
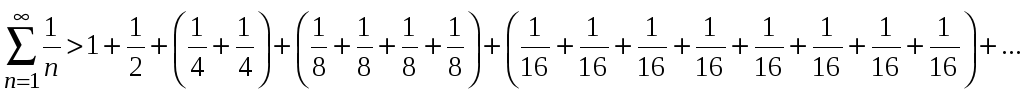 Так
как сумма дробей в каждой скобке равняется
½, имеем
Так
как сумма дробей в каждой скобке равняется
½, имеем
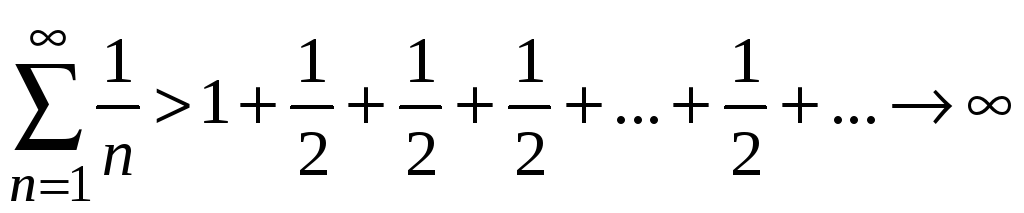 при
при
![]() ,
т. е. ряд расходится.
,
т. е. ряд расходится.
Необходимо также отметить, что если отбросить любое конечное (большое) число членов этого ряда, сумма его останется бесконечно большой.
8.3. Классификация числовых рядов в зависимости от знаков их членов
Ряд называется знакоопределенным, если все его члены одного знака.
Ряд называется знакоположительным (знакоотрицательным), если все его члены положительные (отрицательные).
Ряд называется знакопеременным, если его члены изменяют знаки каким-либо образом.
Ряд называется знакочередующимся, если знаки его членов чередуются (изменяются периодически).
8.4. Достаточные признаки сходимости знакоположительных
числовых рядов
8.4.1. Признаки сравнения рядов
Теорема 8.2 (Первый признак сравнения рядов).
1. Если члены
знакоположительного ряда
![]() не превосходят соответствующих членов
сходящегося ряда
не превосходят соответствующих членов
сходящегося ряда
![]() ,
т. е.
,
т. е.
![]() ,
то он сходится.
,
то он сходится.
2. Если члены
знакоположительного ряда
![]() не меньше соответствующих членов
расходящегося ряда
не меньше соответствующих членов
расходящегося ряда
![]() ,
т. е.
,
т. е.
![]() ,
то он расходится.
,
то он расходится.
Д о к а з а т е л ь
с т в о. Докажем первое утверждение
теоремы. Пусть ряд
![]() сходится и его сумма равна
сходится и его сумма равна
![]() .
.
Ряд
![]() знакоположительный, поэтому
последовательность его n-ых
частичных сумм
знакоположительный, поэтому
последовательность его n-ых
частичных сумм
![]() монотонно возрастает при увеличении
n.
монотонно возрастает при увеличении
n.
Члены ряда
![]() не превосходят соответствующих членов
ряда
не превосходят соответствующих членов
ряда![]() ,
т. е.
,
т. е.
![]() .
Ввиду этого частичные суммы рядов
удовлетворяют неравенству
.
Ввиду этого частичные суммы рядов
удовлетворяют неравенству
![]() .
.
Кроме того, очевидно,
что
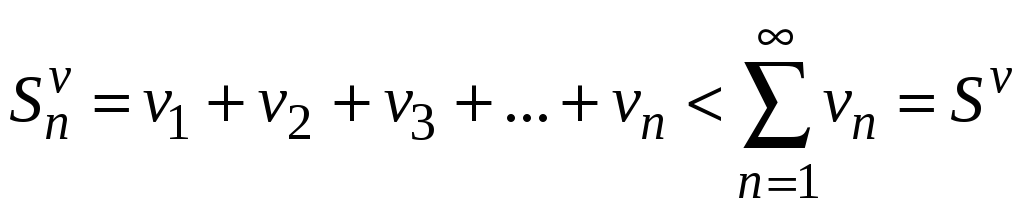 .
Следовательно, последовательность
частичных сумм
.
Следовательно, последовательность
частичных сумм
![]() монотонно возрастает и ограничена (
монотонно возрастает и ограничена (![]() ).
По теореме Вейерштрасса эта
последовательность имеет предел
).
По теореме Вейерштрасса эта
последовательность имеет предел![]() .
Ряд
.
Ряд
![]() сходится.
сходится.
Второе утверждение
теоремы докажем от противного. Пусть
известно, что ряд
![]() расходится и
расходится и
![]() .
Предположим, что ряд
.
Предположим, что ряд
![]() сходится. Тогда по первому утверждению
данной теоремы должен сходиться также
ряд
сходится. Тогда по первому утверждению
данной теоремы должен сходиться также
ряд
![]() .
В этом и состоит противоречие.
.
В этом и состоит противоречие.
Пример 8.4.
Исследовать сходимость ряда
 .
.
Для сравнения
выберем сходящийся ряд, являющийся
бесконечной убывающей геометрической
прогрессией
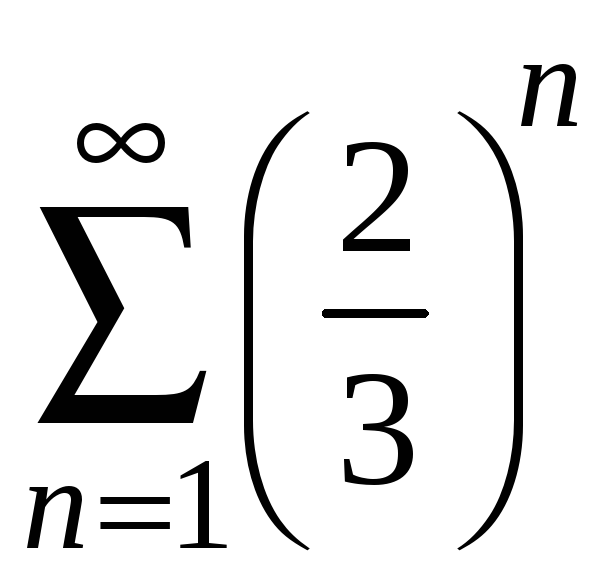 ,
которая сходится, так как знаменатель
прогрессии
,
которая сходится, так как знаменатель
прогрессии
![]() .
Члены исследуемого ряда не превосходят
соответствующих членов предложенной
геометрической прогрессии
.
Члены исследуемого ряда не превосходят
соответствующих членов предложенной
геометрической прогрессии
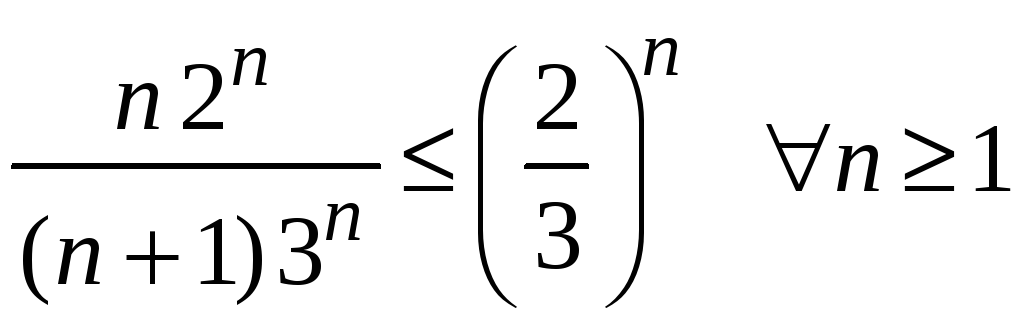 .
В соответствии с пунктом 1 теоремы 8.2
ряд сходится.
.
В соответствии с пунктом 1 теоремы 8.2
ряд сходится.
Пример 8.5.
Исследовать сходимость ряда
 .
.
Для сравнения
выберем расходящийся гармонический
ряд
![]() .
Члены исследуемого ряда больше
соответствующих членов гармонического
ряда
.
Члены исследуемого ряда больше
соответствующих членов гармонического
ряда
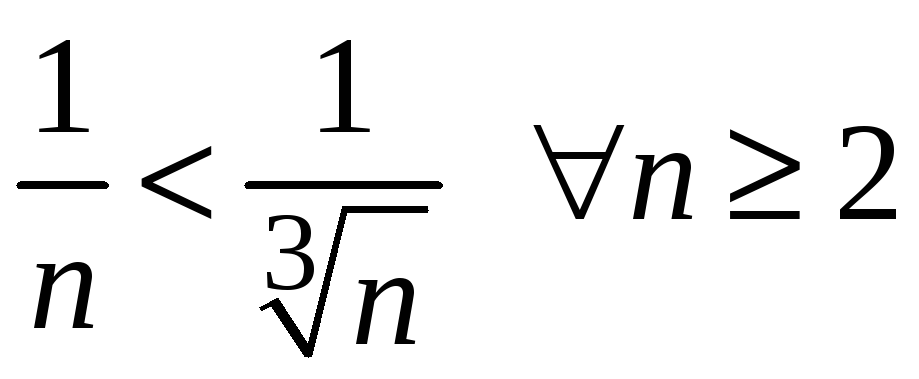 ,
поэтому ряд также расходится.
,
поэтому ряд также расходится.
Теорема 8.3
(Второй признак сравнения рядов). Если
отличен от нуля конечный предел отношения
соответствующих членов двух
знакоположительных рядов
![]() и
и
![]() ,
т. е.
,
т. е.
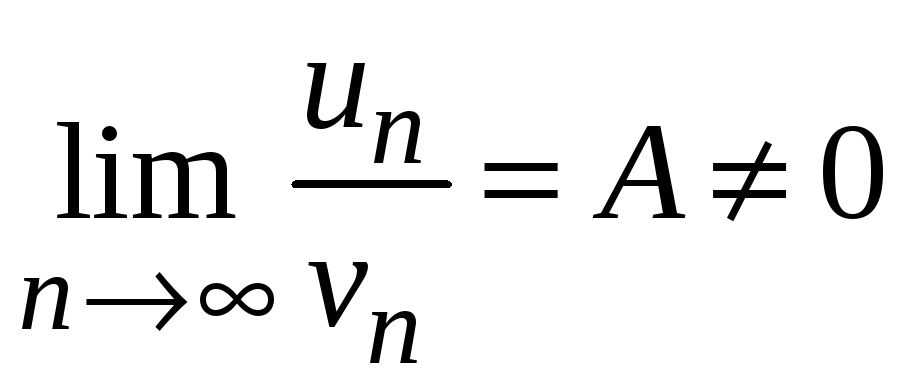 ,
то данные ряды сходятся или расходятся
одновременно.
,
то данные ряды сходятся или расходятся
одновременно.
Д о к а з т е л ь с т в о. По определению предела по Коши на языке - существование предела отношения членов рядов означает:
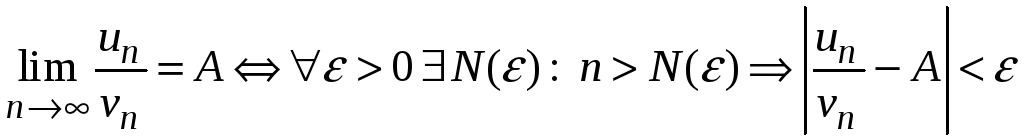 .
.
Это значит, что для любого n > N() справедливы неравенства
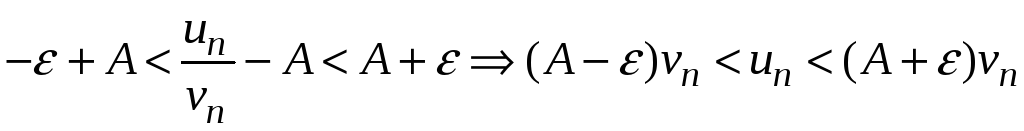 .
.
Сходимость рядов не зависит от того, что будет отброшено конечное число членов (N()). Члены рядов можно перенумеровать и считать, что последнее неравенство выполняется, начиная с n =1. т. е.
![]() .
.
Тогда для частичных сумм рядов можно записать
![]() ,
где
,
где
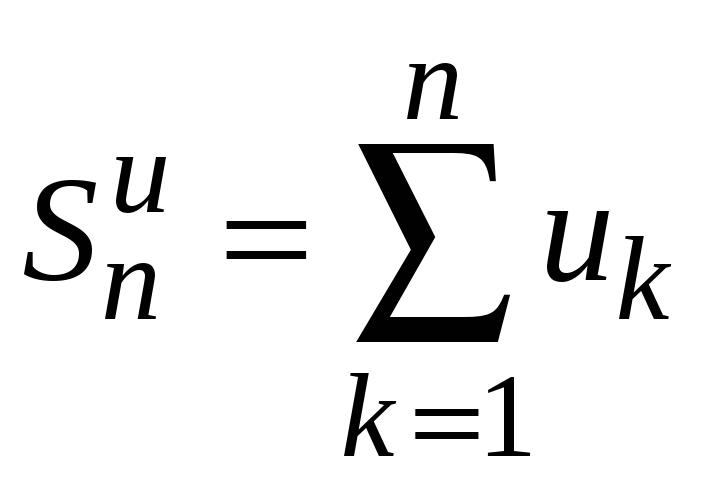 ,
,
 .
.
Далее рассмотрим два случая.
1. Ряд
![]() сходится. Тогда предел его частичных
сумм существует и является конечной
величиной
сходится. Тогда предел его частичных
сумм существует и является конечной
величиной
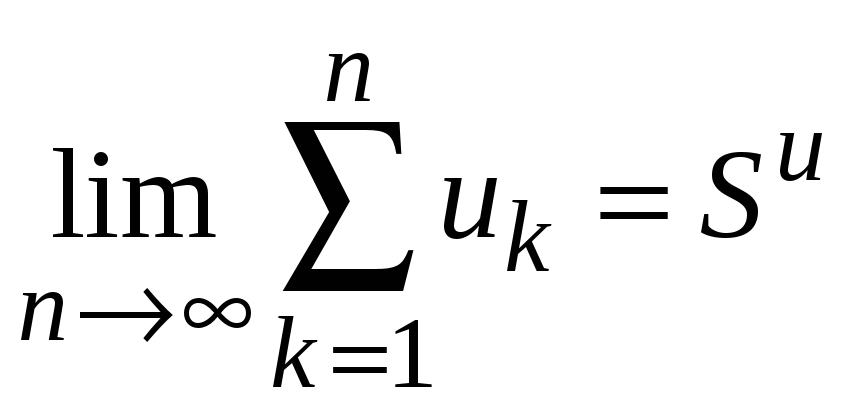 .
Учитывая это и левую часть последнего
неравенства
.
Учитывая это и левую часть последнего
неравенства
![]() ,
можно записать
,
можно записать
![]()
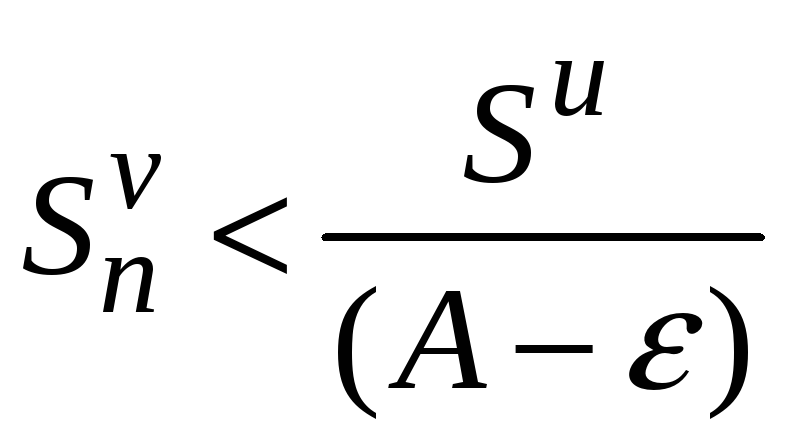 ,
т. е. последовательность частичных сумм
ряда
,
т. е. последовательность частичных сумм
ряда
![]() ,
являющаяся монотонно возрастающей,
ограничена. По теореме Вейерштрасса
она имеет предел и, следовательно, ряд
сходится.
,
являющаяся монотонно возрастающей,
ограничена. По теореме Вейерштрасса
она имеет предел и, следовательно, ряд
сходится.
2. Ряд
![]() расходится, т. е.
расходится, т. е.
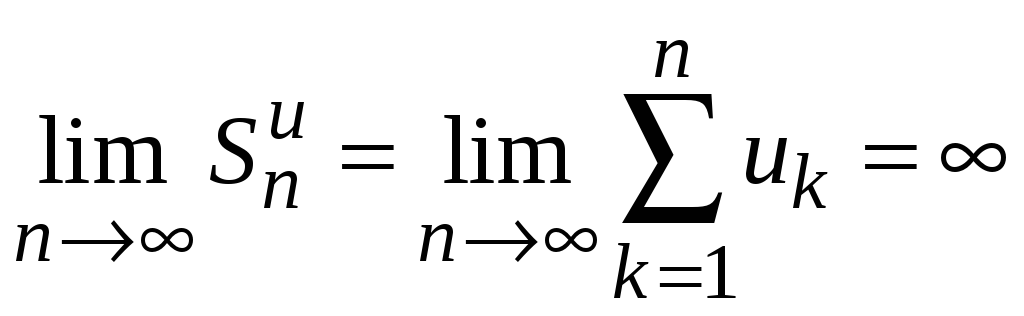 .
Тогда, учитывая правую часть выше
полученного неравенства, имеем
.
Тогда, учитывая правую часть выше
полученного неравенства, имеем
![]() .
Отсюда можно сделать вывод, что предел
частичных сумм второго ряда также
неограничен
.
Отсюда можно сделать вывод, что предел
частичных сумм второго ряда также
неограничен
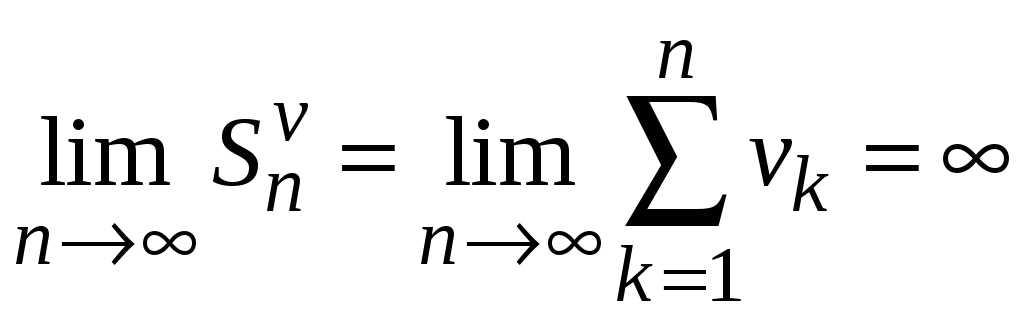 .
Следовательно, ряд
.
Следовательно, ряд
![]() расходится.
расходится.
Можно аналогично
рассуждать, начиная с предположений о
сходимости ряда
![]() ,
показать, что одновременно с ним сходится
или расходится ряд
,
показать, что одновременно с ним сходится
или расходится ряд
![]() .
.
Пример 8.6.
Исследовать сходимость ряда
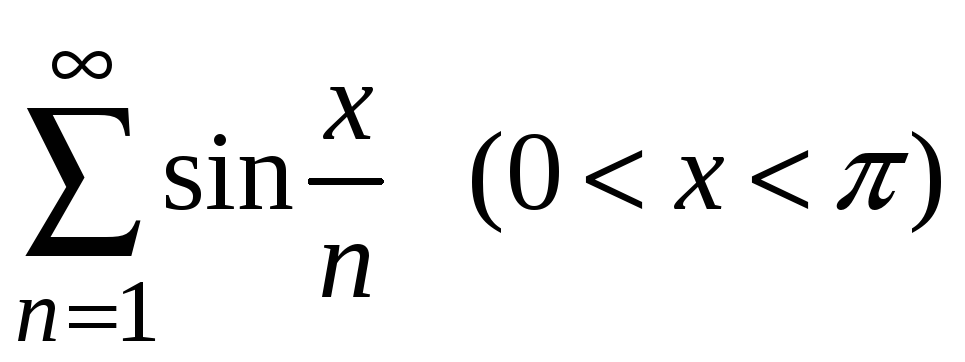 .
.
Сравним исходный
ряд с гармоническим рядом
![]() .
Используем первый замечательный предел,
находим
.
Используем первый замечательный предел,
находим
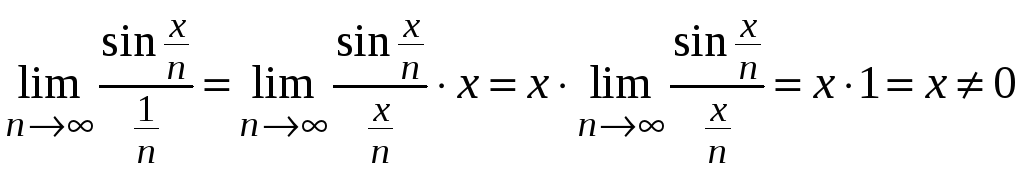 .
.
Отсюда следует, что исследуемый ряд расходится так же, как и гармонический.
Теорема 8.4. (Третий признак сравнения рядов).
1. Если отношение
последующего члена ряда к предыдущему
для ряда
![]() не превосходит соответствующего
отношения последующего члена ряда к
предыдущему для сходящегося ряда
не превосходит соответствующего
отношения последующего члена ряда к
предыдущему для сходящегося ряда
![]() ,
т. е.
,
т. е.
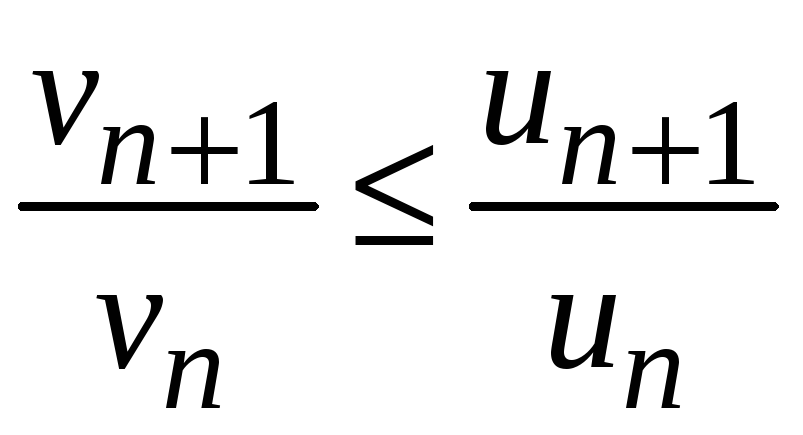 для любого n,
то ряд
для любого n,
то ряд
![]() сходится.
сходится.
2. Если же
 и ряд
и ряд
![]() расходится,
то и ряд
расходится,
то и ряд![]() расходится.
расходится.
Д о к а з а т е л ь с т в о. По условию теоремы для любого n имеют место неравенства
 .
.
Перемножим почленно левые и правые части этих неравенств, получим
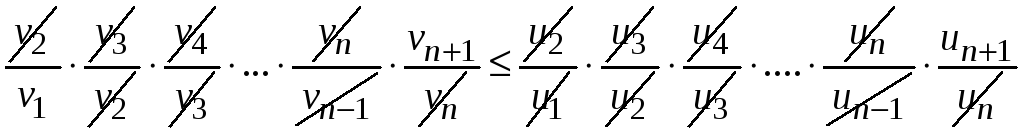 .
.
Сократим одинаковые члены в числителях и знаменателях левой и правой частях неравенства, получим
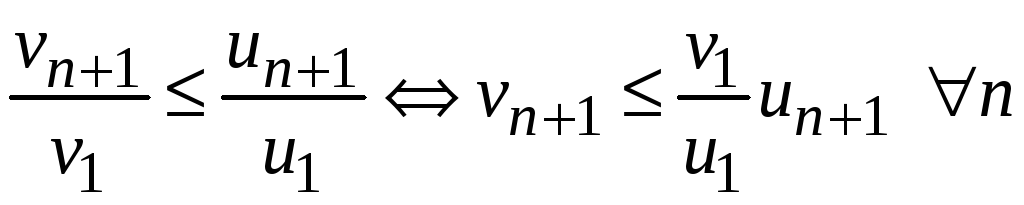 .
.
Отсюда следует,
если ряд
![]() сходится, то по теореме 8.2 сравнения
рядов также сходится ряд
сходится, то по теореме 8.2 сравнения
рядов также сходится ряд
![]() ,
так как его члены не превосходят
соответствующих членов сходящегося
ряда
,
так как его члены не превосходят
соответствующих членов сходящегося
ряда
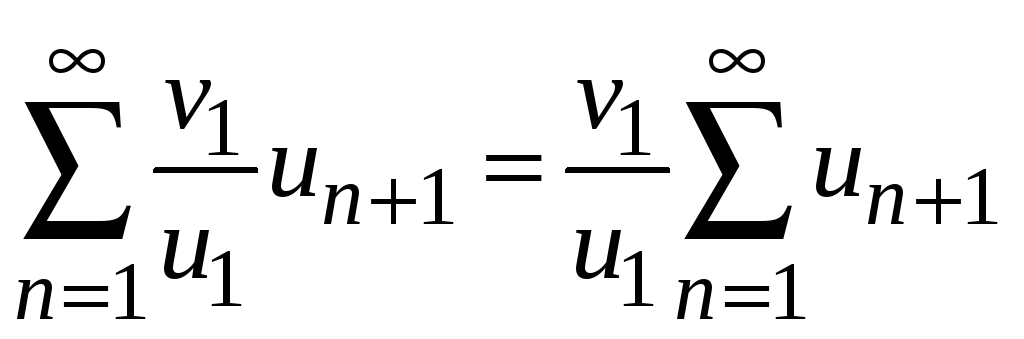 .
На основании той же теоремы, если ряд
.
На основании той же теоремы, если ряд
![]() расходится, то и ряд
расходится, то и ряд
![]() расходится.
расходится.
