8.6. Знакопеременные ряды. Теорема об абсолютной сходимости числового ряда

Теорема 8.8. Числовой ряд сходится, если сходится ряд, составленный из абсолютных величин его членов .

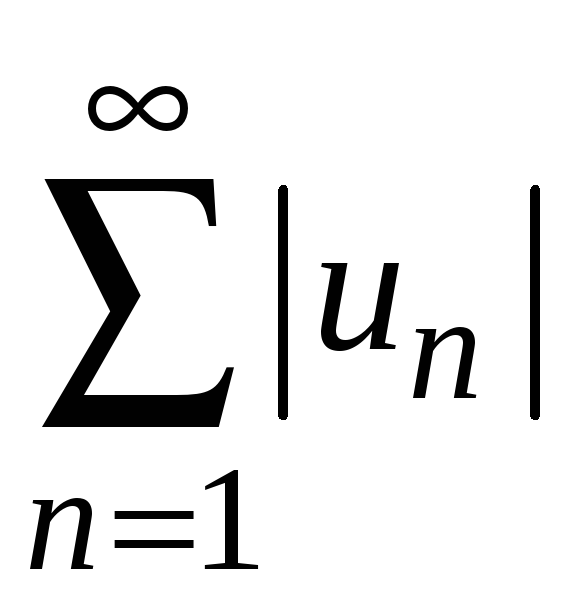Д о к а з а т е л ь с т в о. Пусть ряд 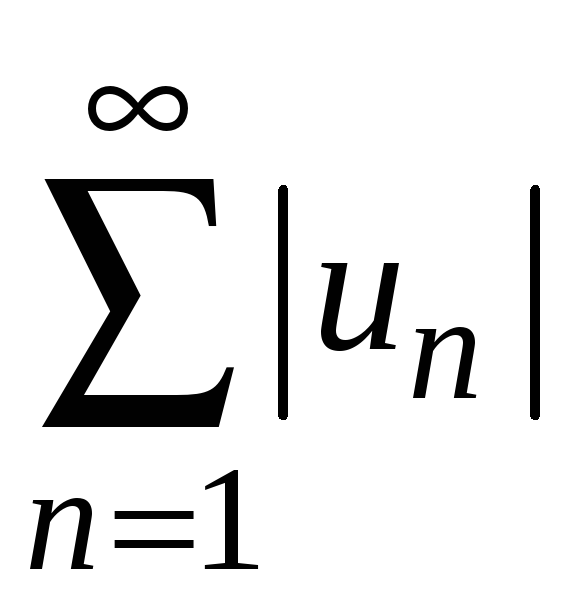сходится. Тогда по свойству 1 сходящихся рядов также сходится ряд .

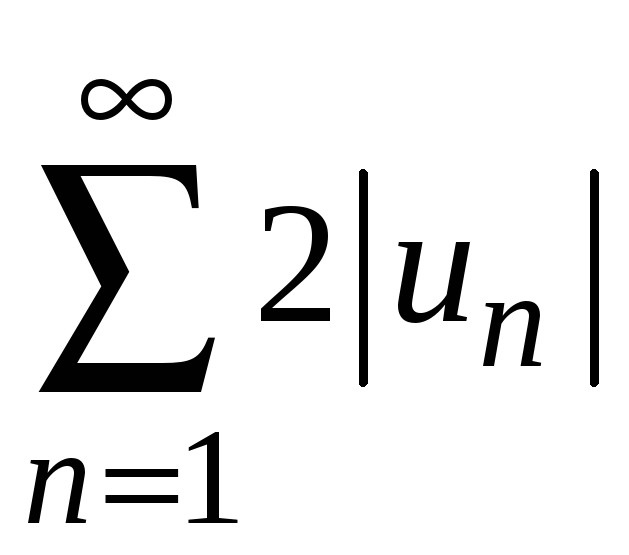Так как , то по первому признаку сравнения рядов (теорема 8.2) также сходится ряд . На основании свойства 2 сходящихся рядов сходится разность двух рядов

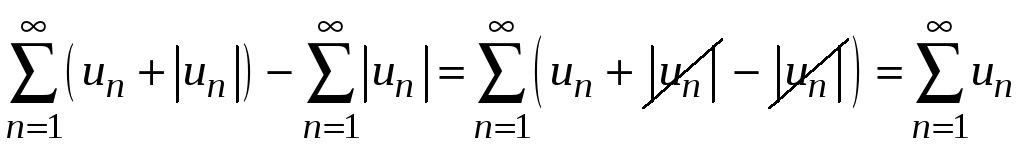, т. е. исходный ряд.

Ряд называется абсолютно сходящимся, если он сходится и сходится ряд, составленный из абсолютных величин его членов.

Ряд называется условно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Пример 8.19. Исследовать сходимость ряда .

Так как и ряд сходится как обобщенно гармонический ряд 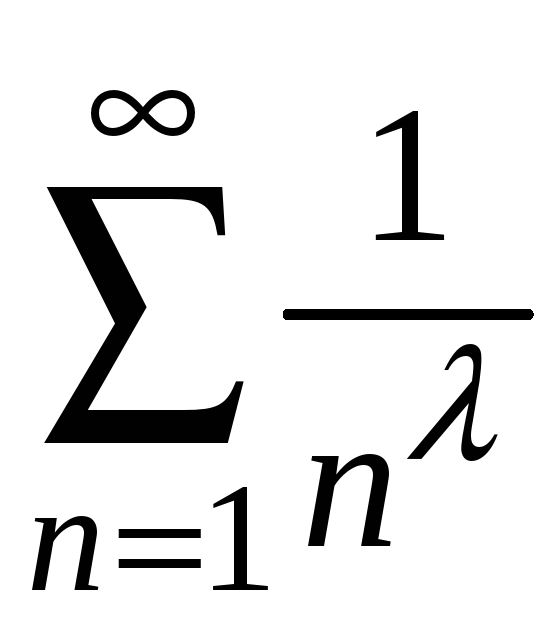при , то по теореме 8.2 сравнения рядов сходится ряд , а по теореме об абсолютной сходимости сходится также ряд 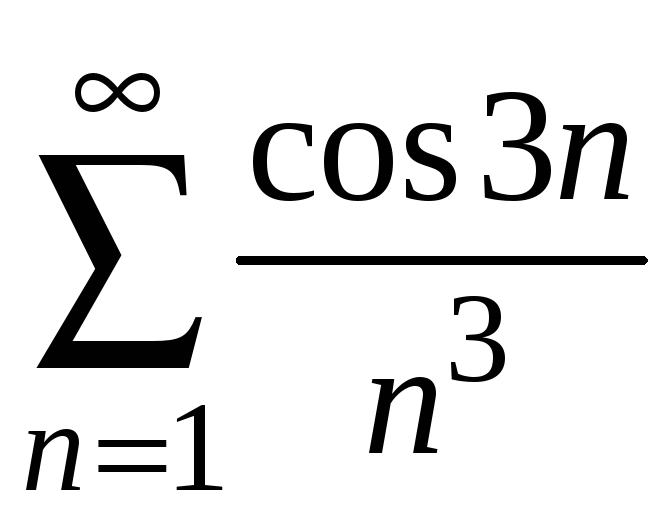. Следовательно, исходный ряд сходится; причем абсолютно.

Пример 8.20. Исследовать на абсолютную сходимость ряд .

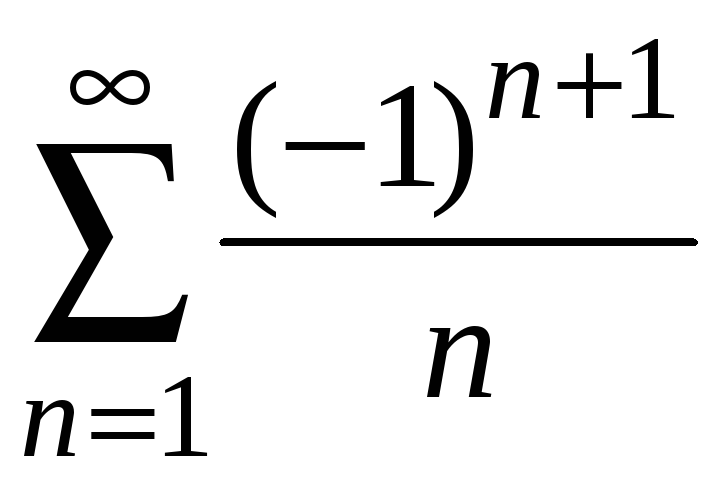Ранее было показано, что данный знакочередующийся ряд сходится (пример 8.15). Ряд, составленный из абсолютных величин данного ряда, является гармоническим, который, как известно, расходится. Это означает, что исходный ряд сходится условно.

Глава 9. Степенные ряды

9.1. Функциональные ряды. Общие понятия

Ряд называется функциональным, если его члены являются функциями некоторой переменной величины х, т. е. он имеет вид

.

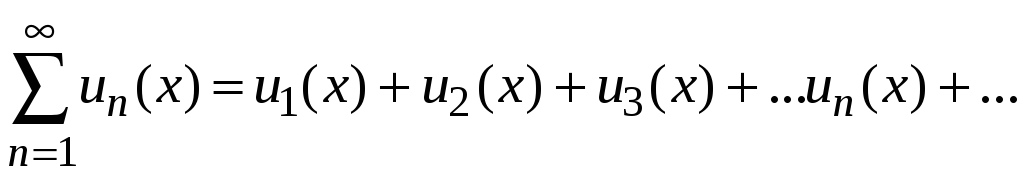При конкретном значении переменной х данный ряд становится числовым и его можно исследовать на сходимость.

Областью сходимости функционального ряда называется множество G всех значений х, при которых ряд сходится.

Сумма n первых членов функционального ряда

называется n-й частичной суммой этого ряда.

Если при любом значении переменной существует предел , то называется суммой ряда,

а разность  остатком ряда.

9.2. Равномерная сходимость функциональных рядов. Теорема Вейерштрасса

Функциональный ряд 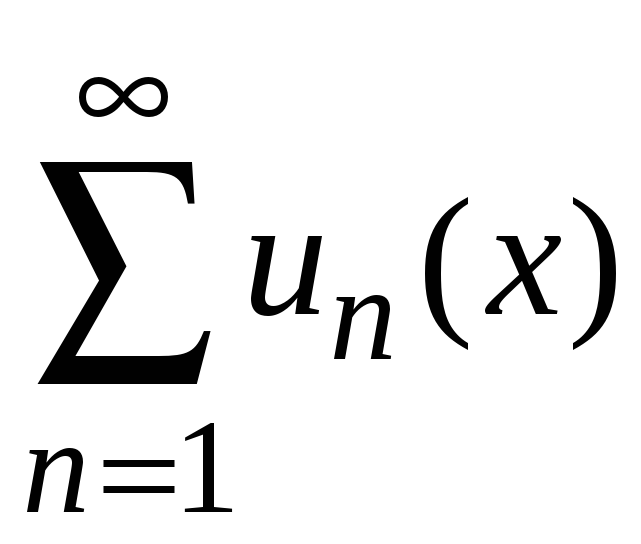называется равномерно сходящимся к сумме в области G, если при сколь угодно малом значении существует такое число , что если , то для любого х из области сходимости ряда G ()

.

Теорема 9.1. (Теорема Вейерштрасса о равномерной сходимости ряда).

Если члены функционального ряда 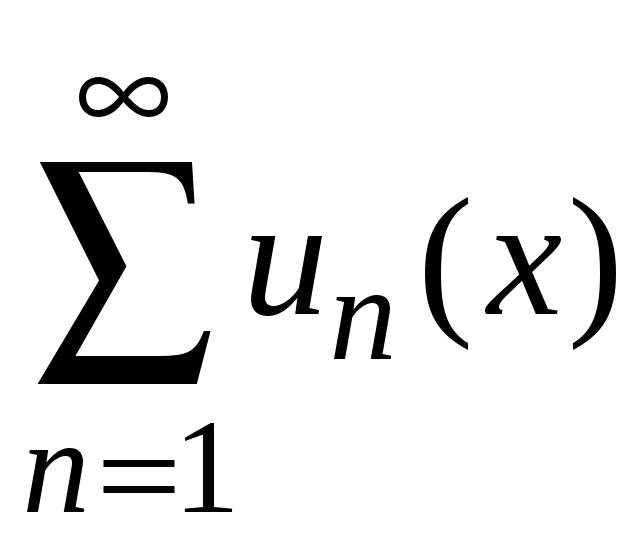на отрезке не превосходят по абсолютной величине соответствующих членов знакоположительного сходящегося числового ряда , т. е. , то ряд сходится абсолютно и равномерно при .

Равномерно сходящиеся ряды обладают рядом важных свойств.

Свойство 1. Если члены ряда 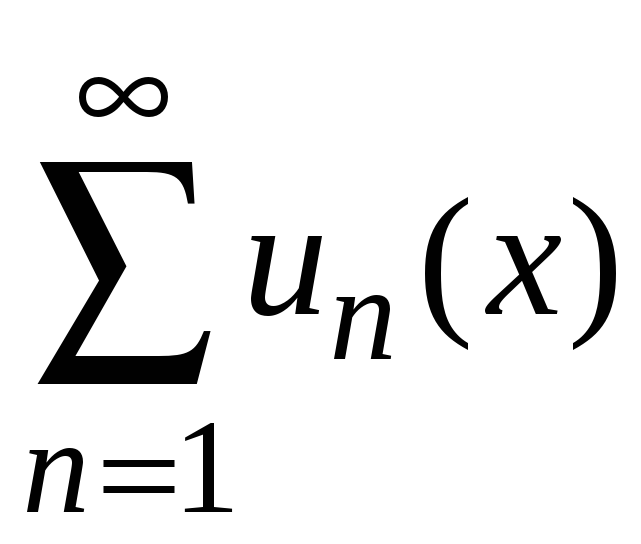определены и непрерывны на отрезке и ряд сходится равномерно к сумме , то эта сумма является непрерывной функцией на этом отрезке.

Свойство 2. Если члены ряда 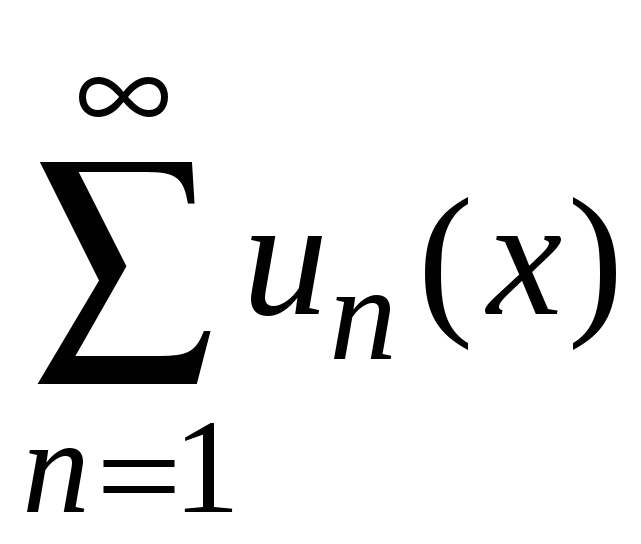являются непрерывными функциями на отрезке и ряд сходится равномерно к сумме , то его можно почленно интегрировать; причем ряд составленный из интегралов его членов равномерно сходится к интегралу суммы ряда, т. е.

.

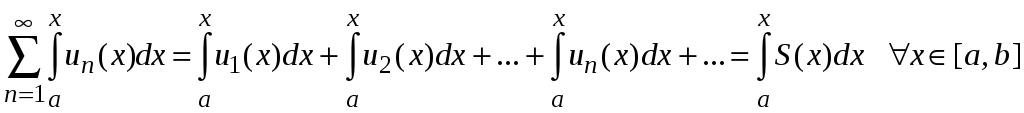Свойство 3. Если члены ряда являются непрерывными функциями на интервале , имеют непрерывные производные на этом интервале и ряд сходится равномерно к сумме , то его можно почленно дифференцировать; причем ряд составленный из производных его членов равномерно сходится к производной суммы ряда, т. е.

.
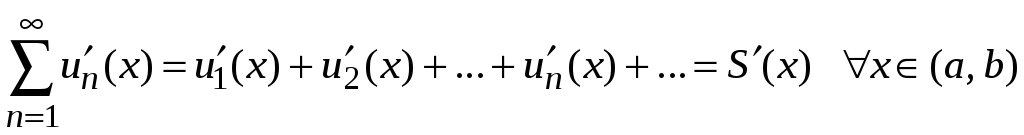