2.2. Уравнения с разделяющимися переменными

Наиболее простым ДУ первого порядка является, уравнение виДа

P(x)•dz+Q(y)•dy=0. (2.5)

В нем одно слагаемое зависит только от х, а другое - от у. Иногда такие ДУ называют уравнениями с разделенными переменными. Проинтегрировав почленно это уравнение, получаем:

- его общий интеграл.

 

Пример 2.2. Найти общий интеграл уравнения х•dx+у•dy=0.

Решение: Данное уравнение есть ДУ с разделенными переменными. Поэтому Обозначим с/2=c_1. Тогда х²-y2=с - общий интеграл ДУ.

Более общий случай описывают уравнения с разделяющимися переменными, которые имеют вид

Особенность уравнения (2.6) в том, что коэффициенты при dx и dY представляют собой произведения двух функций (чисел), одна из которых зависит только от х, другая - только от у.

Уравнение (2.6) легко сводится к уравнению (2.5) путем почленного деления его на Q₁(у)•Р₂(х)≠0. Получаем:

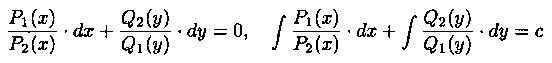
- общий интеграл.

Замечания.

1. При проведении почленного деления ДУ на Q₁(y)•Р₂(х) могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнение Q1(у)•Р2(х)=0 и установить те решения ДУ, которые не могут быть получены из общего решения, - особые решения.

2. Уравнение y^'=ƒ₁(х)•ƒ₂(y) также сводится к уравнению с разделенными переменными. Для этого достаточно положитьи разделить переменные.

3. Уравнение y^'=ƒ(ах+by+с), где а,b,с - числа, путем замены ах+by+с=u сводится к ДУ с разделяющимися переменными. Дифференцируя по х, получаем:

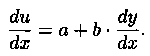
Данное уравнение принимает видоткуда следует

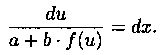
Интегрируя это уравнение и заменяя u на ах+by+с, получим общий интеграл исходного уравнения.

 

Пример 2.3. Решить уравнение (y+xy) •dx+(х-xy)•dy=0.

Решение: Преобразуем левую часть уравнения:

у•(1+х) • dx+х • (1-у)•dу=0.

 Оно имеет вид (2.6). Делим обе части уравнения на ху≠0:

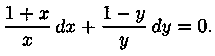
Решением его является общий интеграл х+ln|x|+ln|y|-у=с, т. е. ln|ху|+х-у=с.

Здесь уравнение Q₁(у)•Р₂(х)=0 имеет вид ху=0. Его решения х=0, у=0 являются решениями данного ДУ, но не входят в общий интеграл. Значит, решения х=0, у=0 являются особыми.

Пример 2.4. Решить уравнениеудовлетворяющее условию у(4)=1

Решение: Этот пример представляет собой решение задачи 2 из п. 1.2. Имеем: Проинтегрировав, получим:

т. е.- общее решение ДУ.

Оно представляет собой, геометрически, семейство равносторонних гипербол. Выделим среди них одну, проходящую через точку (4; 1). Подставим х=4 и у=1 в общее решение уравнения: 1=c/4, с=4.

Получаем:- частное решение уравнения

Пример 2.5. Найти общее решение ДУ

Решение: Этот пример демонстрирует решение задачи 1 из п. 1.2. Приведем данное уравнение к виду (2.5):

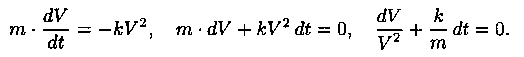
Интегрируем: Отсюда 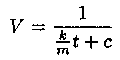- общее решение уравнения.

16. Элементы теории вероятностей. Случайные события.

Основные определения. Будем полагать, что результатом реального опыта (эксперимента) может быть один или несколько взаимоисключающих исходов; эти исходы неразложимы и взаимно исключают друг друга. В этом случае говорят, что эксперимент заканчивается одним и только одним элементарным исходом.

Множество всех элементарных событий, имеющих место в результате случайного эксперимента, будем называть пространством элементарных событий  (элементарное событие соответствует элементарному исходу).

Случайными событиями (событиями), будем называть подмножества пространства элементарных событий  .

Пример 1. Подбросим монету один раз. Монета может упасть цифрой вверх - элементарное событие  _ц (или  ₁), или гербом - элементарное событие  _Г (или  ₂). Соответствующее пространство элементарных событий  состоит из двух элементарных событий:

 = { _ц, _Г } или  = { ₁, ₂}.

Пример 2. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий  = { ₁,  ₂,  ₃,  ₄,  ₅,  ₆}, где  _i- выпадение i очков. Событие A - выпадение четного числа очков, A = { ₂, ₄, ₆}, A .

Пример 3. На отрезке [0, 1] наугад (случайно) поставлена точка. Измеряется расстояние точки от левого конца отрезка. В этом опыте пространство элементарных событий  = [0, 1] - множество действительных чисел на единичном отрезке.

В более точных, формальных терминах элементарные события и пространство элементарных событий описывают следующим образом.

Пространством элементарных событий называют произвольное множество ,  ={}. Элементы  этого множества  называют элементарными событиями.

Понятия элементарное событие, событие, пространство элементарных событий, являются первоначальными понятиями теории вероятностей. Невозможно привести более конкретное описание пространства элементарных событий. Для описания каждой реальной модели выбирается соответствующее пространство .

Событие  называется достоверным событием.

Достоверное событие не может не произойти в результате эксперимента, оно происходит всегда.

Пример 4. Бросаем один раз игральную кость. Достоверное событие состоит в том, что выпало число очков, не меньше единицы и не больше шести, т.е.  = { ₁,    ₂,    ₃,    ₄,    ₅,    ₆}, где  _i- выпадение i очков, - достоверное событие.

Невозможным событием называется пустое множество .

Невозможное событие не может произойти в результате эксперимента, оно не происходит никогда.

Случайное событие может произойти или не произойти в результате эксперимента, оно происходит иногда.

Пример 5. Бросаем один раз игральную кость. Выпадение более шести очков - невозможное событие .

Противоположным событию A называется событие, состоящее в том, что событие A не произошло. Обозначается , .

Пример 6. Бросаем один раз игральную кость. Событие A - выпадение четного числа очков, тогда событие - выпадение нечетного числа очков. Здесь  = { ₁,  ₂,  ₃, ₄,  ₅, ₆}, где  _i- выпадение i очков, A = { ₂, ₄, ₆}, = .

Несовместными событиями называются события A и B, для которых A B = .

Пример 7. Бросаем один раз игральную кость. Событие A - выпадение четного числа очков, событие B - выпадение числа очков, меньшего двух. Событие AB состоит в выпадении четного числа очков, меньшего двух. Это невозможно, A = { ₂, ₄, ₆}, B = { ₁}, AB = , т.е. события A и B - несовместны.

 

Действия со случайными событиями

Суммой событий A и B называется событие, состоящее из всех элементарных событий, принадлежащих одному из событий A или B. Обозначается A + B.

Пример 8. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий = { ₁,  ₂,  ₃, ₄,  ₅, ₆}, где элементарное событие  _i- выпадение i очков. Событие A - выпадение четного числа очков, A = { ₂, ₄, ₆}, событие B - выпадение числа очков, большего четырех, B = { ₅,  ₆}.

Событие A + B = { ₂, ₄,  ₅,  ₆} состоит в том, что выпало либо четное число очков, либо число очков большее четырех, т.е. произошло либо событие A, либо событие B. Очевидно, что A + B .

Произведением событий A и B называется событие, состоящее из всех элементарных событий, принадлежащих одновременно событиям A и B. Обозначается AB.

Пример 9. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий  = { ₁,  ₂,  ₃, ₄,  ₅, ₆}, где элементарное событие  _i- выпадение i очков. Событие A - выпадение четного числа очков, A = { ₂, ₄, ₆}, событие B - выпадение числа очков, большего четырех, B = { ₅,  ₆}.

Событие A B состоит в том, что выпало четное число очков, большее четырех, т.е. произошли оба события, и событие A и событие B, A B = { ₆} A B  .

Разностью событий A и B называется событие, состоящее из всех элементарных событий принадлежащих A, но не принадлежащих B. Обозначается A\B.

Пример 10. Бросаем один раз игральную кость. Событие A - выпадение четного числа очков, A = { ₂, ₄, ₆}, событие B - выпадение числа очков, большего четырех, B = { ₅,  ₆}. Событие A\ B = { ₂, ₄} состоит в том, что выпало четное число очков, не превышающее четырех, т.е. произошло событие A и не произошло событие B, A\B  .

Очевидно, что

A + A = A, AA = A, .

Нетрудно доказать равенства:

, (A+B)C= AC + BC.

Определения суммы и произведения событий переносятся на бесконечные последовательности событий:

, событие, состоящее из элементарных событий, каждое из которых принадлежит хотя бы одному из;

, событие, состоящее из элементарных событий, каждое из которых принадлежит одновременно всем .

Вероятность события. Аксиоматическое определение вероятности

Пусть  - произвольное пространство элементарных событий, а - такая совокупность случайных событий, для которой справедливо:  , AB, A+B и A\B, если A и B .

Числовая функция P, определенная на совокупности событий , называется вероятностью, если:

1. P(A) 0 для любого A из ;

2. P( ) = 1;

3. если A и B несовместны, то P(A+B) = P(A) + P(B);

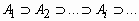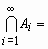
4. для любой убывающей последовательности событий {A_i}из ,, такой, что 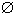, имеет место равенство .

Тройку называют вероятностным пространством.

Вероятность события. Классическое определение вероятности

Пусть = { ₁,  ₂, …,  _s} - произвольное конечное пространство элементарных событий, A - событие, состоящее из k элементарных событий: A={ _i1,  _i2, …,  _ik}, 1 i₁ i₂ … i _k s, k = 1, 2,…, s, и пусть . Определенная таким образом функция P(A) удовлетворяет всем аксиомам 1-4(здесь множество состоит из всех подмножеств множества  : ). Таково классическое определение вероятности события A.

Принята следующая формулировка классического определения вероятности: вероятностью события A называется отношение числа исходов, благоприятствующих A, к общему числу исходов.

Из приведенных определений следует: P()=0, , .

Вероятность суммы событий

Для любых двух событий A и B справедливо: .

Если события A и B несовместны, то .

Вероятность произведения событий. Условная вероятность. Независимые события

Условная вероятность P(A/B) события A при условии, что событие B произошло, P(B) > 0, определяется формулой

.

Для любых двух событий A и B справедливо: .

События A и B называются независимыми, если . Для любых двух независимых, событий A и B справедливо: .

Формула полной вероятности. Формулы Байеса

Пусть A - произвольное событие, а события B₁, B₂, …, B_n - попарно несовместны и образуют полную группу событий, т.е. . Тогда имеет место следующая формула для вероятности события A - формула полной вероятности -

, где P(B_k)>0, k=1, 2, …, n, A B₁+ B₂ + …+ B_n.

Если событие A произошло, то вероятность того, что имело место событие B_k

вычисляется по формуле Байеса: .