
- •1 Функция. Постоянные и переменные величины. Одз. График ф-ий. Способы задания ф-ий.
- •2 Сложная,обратная,неявная ф-ии. Четная и нечетная ф-ия. Периодическая ф-ия. Ограниченная ф-ия.
- •3 Предел ф-ии. Определение. Геометрический смысл предела.
- •5 Теорема3,следствие,4,5.
- •6 Односторонние пределы. Определение предела слева и предела справа.
- •7 Бесконечно малые и бесконечно большие величины. Теоремы о бесконечно малых. Теорема1.
- •8 Теорема 2. Следствия 1,2,3. Замечание об отношении 2б.М.
- •9. Теоремы о пределах. Теоремы1,2,следствие,3.
- •10. Теорема4(предел частного)
- •12 Первый замечательный предел.
- •13 Число е. Второй замечательный предел и его следствия.
- •15 Теоремы о непрерывных ф-ях. Теорема1,2,3,4
- •16 Типы точек разрыва. Устранимый разрыв. Разрывы 1,2 рода. Скачок.
- •17 Производная. Геометрический и механический смысл. Уравнение касательной.
- •18 Зависимость между непрерывностью и диф-тью ф-ий.
- •20 Производные обратных тригонометрических ф-ий.
- •21 Производная сложной ф-ии.
- •26 Геометрический смысл диф-ла.
- •27 Применение дифференциала к приближенным вычислениям.
- •28. Приложение производной. Теорема Ферма. Ее геометрический смысл.
- •29.Теорема Роля.
- •30.Теорема Коши.
- •31.Теорема Лагранжа.Ее геом смысл.Следствия1,2.
- •32.Правило Лоиталя.Теорема.
- •33.Возрастание и убыв ф-ии.
- •Часть 2 док-ть сам-но
- •34.Экстремумы ф-ии. Теорема3.
- •35.Теоремы 4,5.
- •36.Теорема6.
- •37.Выпуклость и вогнутость ф-ии.Теорема7.
- •38.Точка перегиба.Теорема8.
- •42. Таблица неопределенных интегралов
- •47. Приближенное вычисление определенных интервалов
- •48. Несобственные интегралы.
- •49. Разложение многочлена по формуле Тейлора.
- •51. Экстремум ф-ии нескольких переменных
- •52. Метод наименьших квадратов.
- •56. Д/у II порядка.Понижение порядка д/у.
- •57.Линейные д/у II порядка.Линейная независ ф-ий.Критерий лин. Независимости.
- •58.Теорема1(об общем реш-ии лин однор-го д/у II порядка).
- •59.Лин однор-ое д/у с постоянными коэффициентами.
- •60.Теорема2(общем реш-ии лин неоднор-го д/у II порядка).
- •61.Линейные неоднородные д/у II порядка с пост. Коэфициентами.
18 Зависимость между непрерывностью и диф-тью ф-ий.
Теорема 1.
Если ф-ия f(x) дифференцируема в некоторой точке, то она непрерывна в этой точке
Док-во.
Пусть ф-ия y=f(x) дифференцируема в точке x тогда существуют
y’(x)= ; (∆x≠0)
∆y=
*∆x
=>
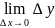 =
=
Δy→0
Δx→0
Значит ф-ия непрерывна на основании 1 определения непрерывности.
Справедливо ли обратное?
Нет, существует например y=׀x׀

В 0 производная не существует, а ф-ия непрерывна.
20 Производные обратных тригонометрических ф-ий.
Производная обратной ф-ии для данной дифференцируемой ф-ии будет равна обратной величине производной данной дифференцируемой ф-ии.
X’y=
док-во.
Если ф-ия монотонна и непрерывна, то она имеет обратную
y’(x)
f’(x)≠0
f’(x)>0
f’(x)<0
если производная отлична от нуля значит ф-ия либо возрастает либо убывает и монотонна
x(y)=g(y)
x’y=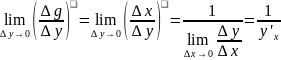
Δx→0 => Δy→0
21 Производная сложной ф-ии.
Производная сложной ф-ии.
y=f(z) zє(A;B)
z=φ(x); xє(α;β)
E[φ(x)]=(A;B), область изменения y=f[φ(x)], xє(α;β).
Пусть ф-ия y=f(z) дифференцируема по z, а ф-ия z=φ(x) диф-ма по x.
Теорема.
Производная сложной ф-ии y=f(z) если ф-ия y=f(z) и z=φ(x) диф-мы по своим аргументам равна производной ф-ии y по промежуточному аргументу z умноженной на производную промежуточного аргумента z по x.
Док-во.
y’z=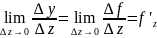
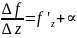 =>
Δf=(f’z+α)Δz
(1)
=>
Δf=(f’z+α)Δz
(1)
Разделим на Δx
 (2)
(2)

F’x=f’z*z’x
22 Производная неявной ф-ии.
При дифференцировании неявной ф-ии считают что вместо y представлена ф-ия y(x) и дифференцируют по x построчно, а затем находят y’(x)
Напр.: x2+y2=a2
x2+[y(x)]2=a2,
2x+2y(x)*y’(x)=0,
y’(x)=-x/y
23 Таблица производных.
(C)’=0
(x)’=1
(u+v-w)’=u’+v’-w’
(uv)’=u’v+uv’
(
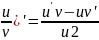
(sin*u)’=cosu*u’
(cos*u)’=sinu*u’
(
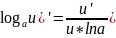

(au)’=auln
(eu)’=eu*u’
(un)’=n*u(n-1)*u’
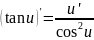
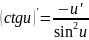
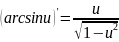
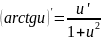
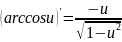
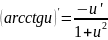
f’x=f’z*z’x
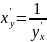
24 Производные высших порядков.
Пусть ф-ия f(x) дифференцируема в некотором промежутке, ее производная f’(x) является ф-ей аргумента x и может случиться что эта ф-ия сама имеет производную. Производная от производной 1-го порядка называется производной 2-го порядка
yu(x)=[f’(x)]’
ynx=[y(n-1)x]’=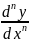 – производная n-ого порядка
– производная n-ого порядка
25.Понятие о диф-ле ф-ии. Св-ва диф-ла.
Главная линейная часть полного приращения ф-ии f(x) называется дифференциалом f(x) в этой точке и обозначается df=f’(x)Δx (8) Δf=df+α*Δx (9)
Формула (8) дает возможность вывести правила по которым рассчитываются дифференциалы суммы, произведения и частного дифференцируемых ф-ий.
dc=0
d(u+v+w)=du+dv+dw

d*(uv)=udv+vdu
dx=Δx
поэтому (8) можно переписать
df=f’(x)dx (10)
f’(x)=
производная дифференцируемой ф-ии равна отношению дифференциала этой ф-ии на дифференциал.
26 Геометрический смысл диф-ла.
Для объяснения геометрического смысла дифференциала вернемся к определению производной. Дана кривая AB, A(x;f(x)); B(x+Δx;f(x+Δx))
BC=Δy, AC=Δx
Рассмотрим ∆ADC где DC=AC*tgα, DC=∆x*f’(x) (11)
Из геометрического смысла следует что
tgα=f’(x)
DC=df=∆x*f’(x)
BC=Δy=DC+BD
∆y=df+BD (12)
DC – есть приращение ординаты касательной, таким образом дифференцируемая ф-ия y=f(x) в данной точке x равен приращению ординаты касательной к графику ф-ии в этой точке когда x получил приращение Δx.
Если ф-ия вогнутая то ∆y>df
Если ф-ия выпуклая то Δy<df
