35.Теоремы 4,5.

Теорема 4 (1 достаточный признак экстремума)

Точка x₀ является точкой экстремума дифференцируемой ф-ии f(x) если производная ф-ии в этой точке равна нулю и при переходе через точку x₀ производная меняет знак: перемена знака с «+» на «-» - x₀-точка максимума, перемена знака с «-» на «+» - точка x₀ – точка минимума. В самой точке x₀ производная =0 или не существует.

Док-во.

Пусть для определенности производная меняет знак с «+» на «-»

1. f’(x)>0, xє(x₀-E,x₀)=>f(x₀)>f(x), xє(x₀-E;x₀)

2. f’(x)<0, xє(x₀;x₀+E)=>f(x₀)>f(x), xє(x₀;x₀+E)

по достаточному признаку возрастания и убывания ф-ии ф-ия возрастает и => из (1) и (2)=>

f(x₀)>f(x), xє(x₀-E;x₀+E), т.е. в точке x₀ – максимум.

2 часть док-ть сам-но.

Теорема 5.

Если ф-ия f(x) дифференцируема в некоторой окрестности точки x₀ ее производная f’(x)=0 обращается в ноль в точке x₀, но при переходе через точку x₀ производная сохраняет постоянный знак, то в точке x₀ ф-ия f(x) не имеет экстремума

Док-ть сам-но

36.Теорема6.

Теорема 6 (2-ой достаточный признак экстремума)

Точка x₀ – точка экстремума дважды дифференцируемой ф-ии f(x) если f’(x₀)=0 а f’’(x₀)≠0, f’’(x₀)>0 причем если 2-ая производная в точке x₀>0 то точка x₀ – точка минимума если же f’’(x₀)<0 – точка максимума.

Док-во

Пусть f’(x₀)=0, f’’(x₀)>0, f’’(x₀)= lim [f’(x₀+Δx₀)-f’(x₀)]/Δx₀>0 {Δx→0}, но если предел больше нуля то сама дробь больше нуля. =>

[f’(x₀+Δx₀)-f’(x₀)]/Δx₀>0;

f’(x₀+Δx₀)/Δx₀>0

1. если Δx<0, f’(x₀+Δx₀)<0

2. если Δx>0, f’(x₀+Δx₀)>0

значит производная меняет знак с «-» на «+»

f’(x)<0, xє(x₀-E,x₀)

f’(x)>0, xє(x₀,x₀+E)

а это значит что в точке x₀ согласно 1-му достаточному условию – минимум.

37.Выпуклость и вогнутость ф-ии.Теорема7.

Говорят что ф-ия f(x) имеет на отрезке [a;b] вогнутость, если соответствующая часть кривой y=f(x) расположена выше касательной проведенной точки M(x,f(x)). Ф-ия имеет выпуклость расположенной ниже касательной проведенной точки M(x,f(x))

Теорема 7 (достаточное условие выпуклости и вогнутости кривой)

1. если для дважды дифференцированной ф-ии y=f(x), f’’(x)>0 в (a;b) то график ф-ии вогнут в данном промежутке

2. если для дважды дифференцированной ф-ии f’’(x)<0 в (a;b) то график ф-ии имеет выпуклость

док-во

проведем нестрогое геометрическое док-во.

Если {f’(x)}’>0, f’(x) – возрастает, т.е. ф-ия вогнутая

Т.е. ф-ия выпуклая.

38.Точка перегиба.Теорема8.

Точка перегиба – точка при переходе через которую кривая меняет свою вогнутость на выпуклость или наоборот.

Теорема 8.

Если в точке x₀ второй производной дифференцируемой ф-ии = 0 ( 1 производная этой точки, вторая производная меняет знак с «+» на «-» или с «-» на «+») то в точке x₀ ф-ия имеет перегиб.

Док-во

f’(x₀)=0, f’’(x₀)=0

f’’(x)>0, xє(x₀-E;x₀)

f’’(x)<0, xє(x₀, x₀+E)

39. асимптоты плоской кривой. Вертикальные асимптоты. Невертикальные асимптоты.

Различают асимптоты вертикальные и невертикальные.

1. Прямая x=a называется вертикальной асимптотой, если 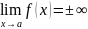, например ,

,

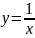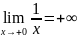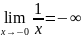
Имеет вертикальную асимптоту x=0

2. Прямая к которой стремится кривая при неограниченном стремлении x→g называется вертикальной асимптотой

Есть ф-ия y=f(x). Расстояние от кривой до асимптоты измеряется перпендикуляром (MK)

MN – наклонная, она больше чем MK, MN>MK

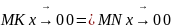, (при x→0) ║

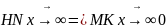
Рассмотрим

MN=f(x)-(kx+b) где k-? b-?

Мы хотим чтобы

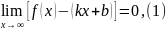
Разделим обе части (1) на x

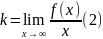
k-коэффициент невертикальной асимптоты

• 

40. Первообразная. Неопределенный интеграл. Следствие 1. Следствие 2. Св-ва неопределенного интеграла.

Дифференциальное исчисление решает задачу нахождения производной или дифференциала известной ф-ии y=f(x).

Интегральное исчисление решает обратную задачу, по известной ф-ии y=f(x), которая является производной некоторой непрерывной ф-ии, найти эту ф-ию.

Первообразной непрерывной ф-ии y=f(x) называется ф-ия F(x) производная которой равна f(x).

F(x):F’(x)=f(x)

f(x) – известная непрерывная ф-ия, а F(x) – неизвестная

напр. Ф-ия f(x)=3x², F(x)=x³+c, где c – произвольная постоянная => первообразная определяется не единственным образом.

Следствие 1.

Две первообразные одной и той же ф-ии (непрерывной) f(x) отличаются друг от друга на постоянное слагаемое

Дано

F₁(x), F₂(x)

F’₁(x)=f(x)

F’₂(x)=f(x)

Составим вспомогательную ф-ию

G(x)=F₁(x)-F₂(x)

G’(x)=F’₁(x)-F’₂(x)=f(x)-f(x)=0 =>G(x)=const=c => F₁(x)-F₂(x)=c => F₁(x)=F₂(x)+c

Следствие 2.

Прибавляя к первообразной непрерывной ф-ии f(x) произвольные постоянные можно получить весь запас первообразных

Док-во.

1. Мы покажем, что любые 2 первообразные отличаются друг от друга на постоянное слагаемое, т.е. если F₁(x), F₂(x), то F₁(x)=F₂(x)+c

2. Если мы возьмем F(x), которая является первообразной для f(x), то и F(x)+c также будет являться первообразной ф-ии f(x)

(F(x)+c)’=F’(x)+c’=F’( c)=f(x)

Тем самым весь запас первообразных исчерпан, т.е. других первообразных кроме F(x)+c не существует

Определение

Неопределенным интегралом непрерывной ф-ии f(x) называется весь запас ее первообразных (ввел Лейбниц)

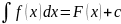(4)

Свойства неопределенного интеграла

1. Производная неопределенного интеграла равна подынтегральной ф-ии

Дифференциал от неопределенного интеграла равен подынтегральному выражению

Для док-ва продифференцируем обе части (4)

Если производные равны, то интегралы отличаются на постоянное слагаемое, но поскольку интегралы вычисляются с точностью до const то интегралы равны

2. Постоянный множитель можно выносить за знак неопределенного интеграла

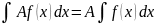(5)

Для доказательства нужно взять производные от обеих частей (5)

Af(x)=A(f(x))

3. Неопределенный интеграл от алгебраической суммы непрерывных ф-ий равен такой же алгебраической сумме интегралов от этих ф-ий

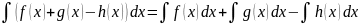
4. Действительно

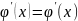
41. Основные методы интегрирования.

1. Метод разложения

В методе разложения используется III сво-во неопределенного интеграла, т.е.

f(x)=f₁(x)+f₂(x), то

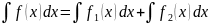
Этот метод используется в том случае, если ф-ия f(x) неинтегрируемая, может быть представлена в виде суммы интегрированных ф-ий

Напр.

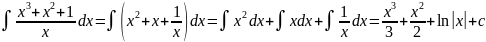
2. Метод интегрирования по частям

Известно, что d(uv)=udv+vdu, отсбда udv=d(uv)-vdu (6)

Проинтегрируем обе части (6)

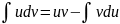(7)

Формула (7) называется формулой интегрирования по частям. Предполагается, что ф-ии u(x) и v(x) обладают следующими свойствами:

Обе дифференцируемы по x, ф-ия v(x) интегрируема по X.

Следует правильно выбирать ф-ии u(x) и v(x)

U(x): arcsinx, arccosx, arctgx, arcctgx, lnx

Ф-ию xⁿ желательно взять за v(x)

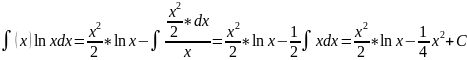
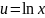
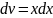
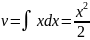3. Метод подстановки.

Есть 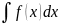положим 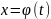, тогда

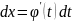
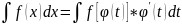
Формула записана слева направо, но формула работает тогда, когда и наоборот

Докажем обратное. Фозьмем ф-ии F[φ(t)] и рассмотрим ее производную