
- •Глава III. Линейные преобразования
- •3.1. Матрица линейного преобразования
- •3.2. Ядро и образ линейного преобразования
- •3.3. Собственные значения квадратной матрицы
- •1. Найти собственные значения матриц:
- •3.4. Собственные векторы квадратной матрицы
- •3.5. Свойства собственных векторов матрицы
- •3.6. Базис пространства , состоящий из собственных векторов матрицы
- •3.7. Норма линейного преобразования
- •Ортогональные матрицы
- •3.9. Симметрические преобразования и симметрические матрицы
- •Собственные значения симметрической матрицы
- •Собственные векторы симметрической матрицы
Собственные векторы симметрической матрицы
Ниже будет доказано, что в пространстве имеется ортонормированный базис, состоящий из собственных векторов симметрического преобразования. Сначала докажем следующие леммы.
Лемма 1.
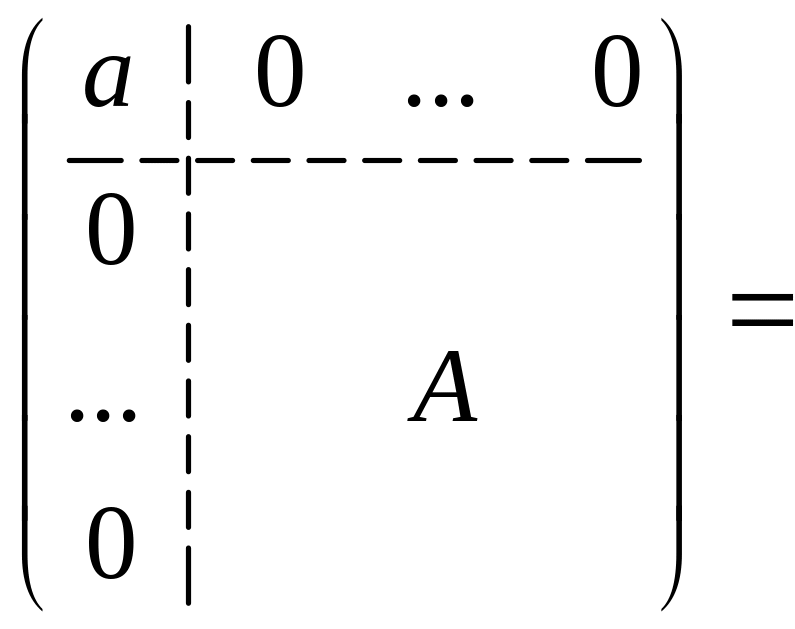
Даны две
матрицы
![]() и
и
![]() порядка n
порядка n
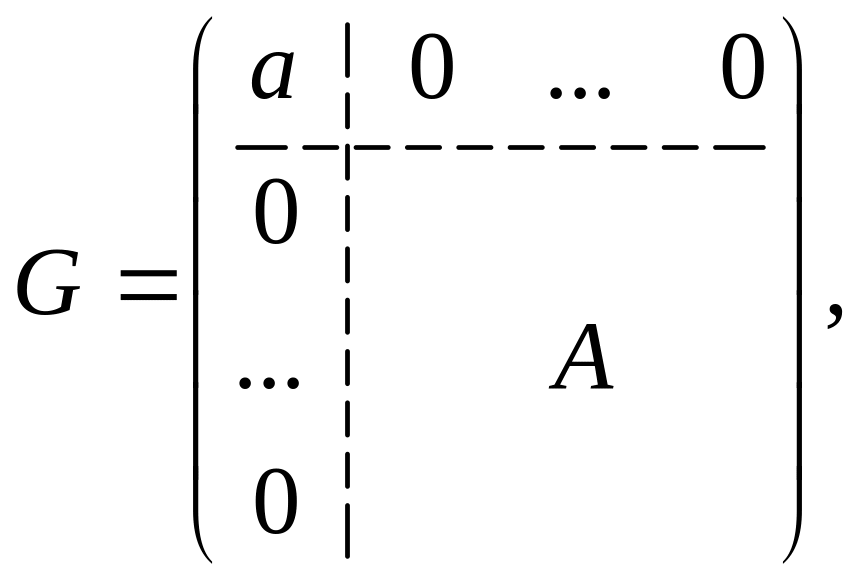
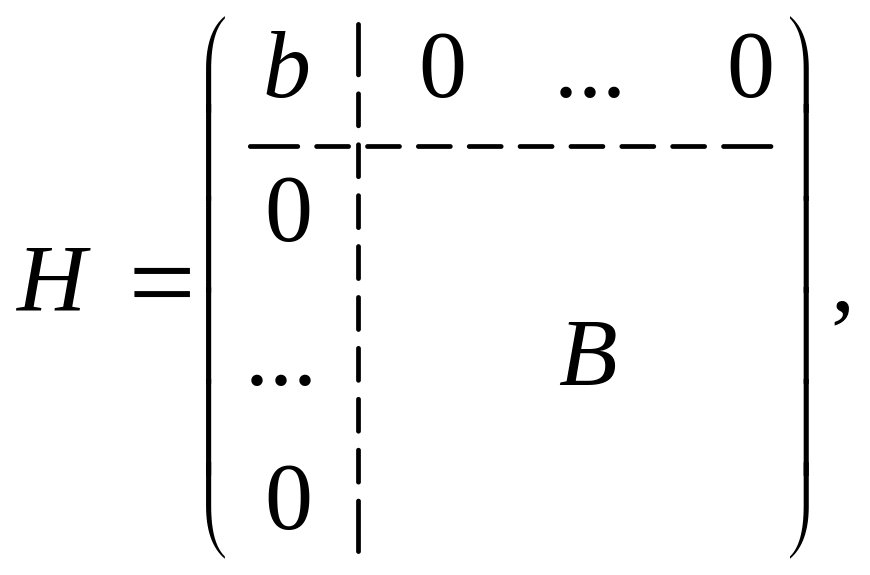
где
и
–
матрицы порядка
![]() .
Тогда
справедливы следующие утверждения:
.
Тогда
справедливы следующие утверждения:
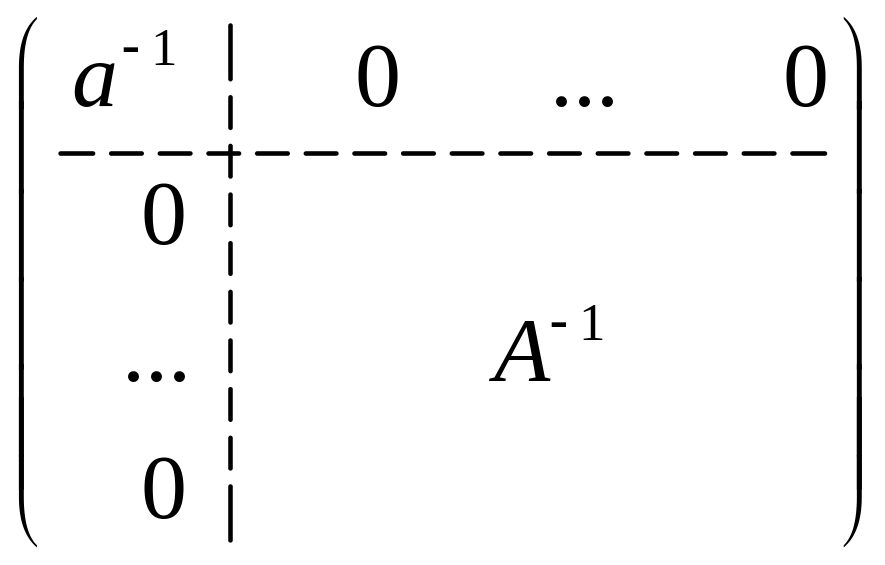
1.
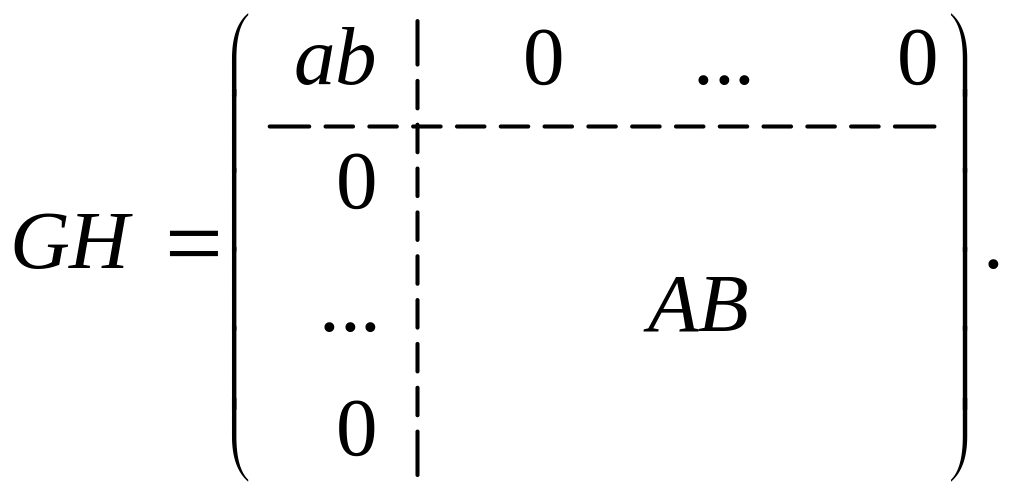
2 . Если матрица
обратима и
![]() ,
то матрица
обратима и
,
то матрица
обратима и
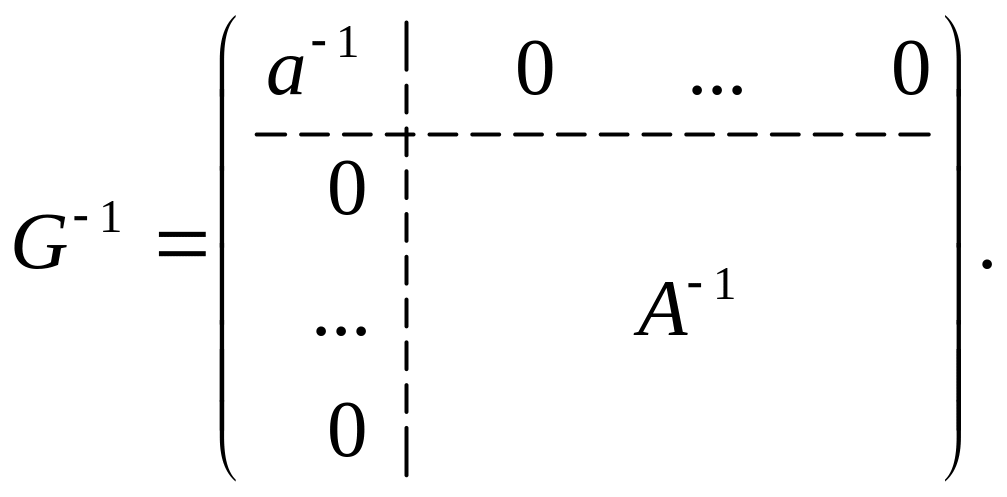
3.
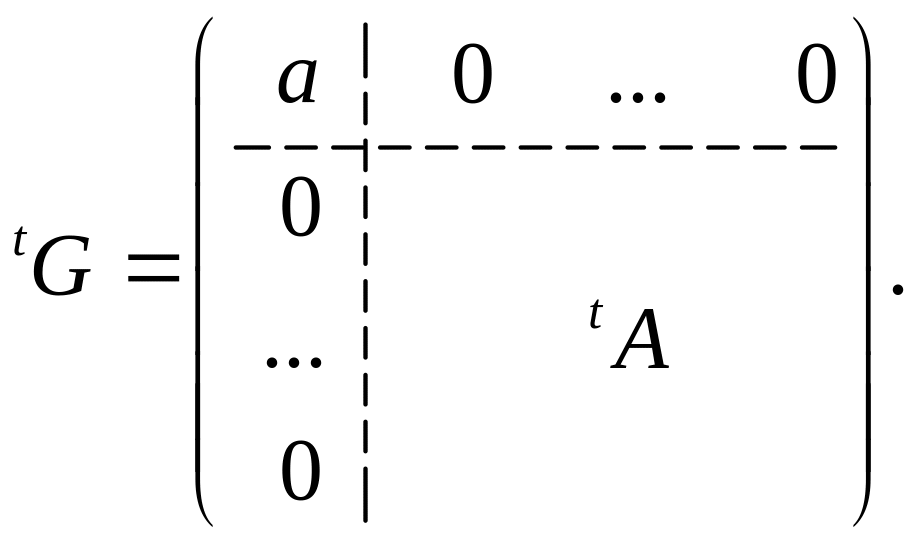
Доказательство
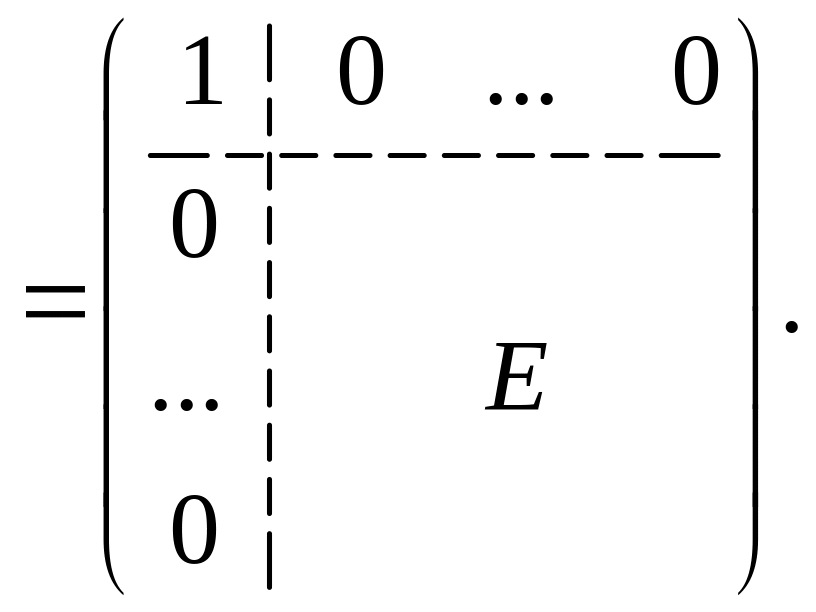
Найдем первую строку и первый столбец матрицы
![]()
![]()
Теперь найдем
элемент матрицы
,
расположенный в
![]() -й
строке и
-й
строке и
![]() -м
столбце,
-м
столбце,
![]() ,
,
![]()
![]() .
.
2. Используя доказанное выше первое утверждение леммы, имеем
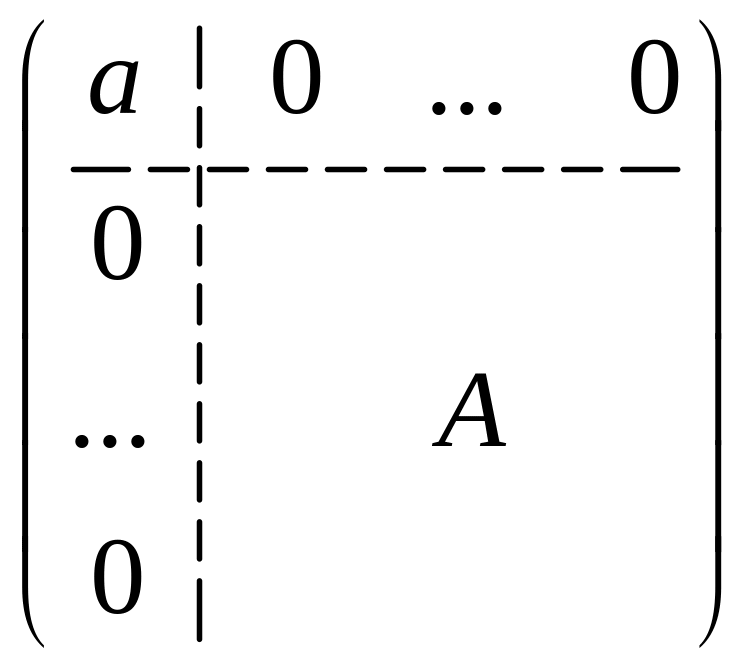
 =
=
3.
![]()
![]() ,
,
![]() .
■
.
■
□ Лемма 2. Если – ортогональная матрица порядка , то

− ортогональная матрица порядка n.
Доказательство.
Из ортогональности матрицы
следует, что
![]() (теорема 1.16). Ортогональность матрицы
(теорема 1.16). Ортогональность матрицы
![]() будет вытекать из равенства
будет вытекать из равенства
![]() ,
которое установим, используя лемму 1
,
которое установим, используя лемму 1
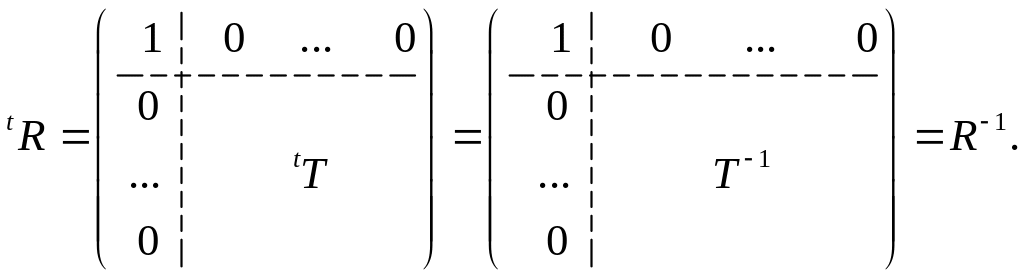 ■
■
Построение ортонормированного базиса , состоящего из собственных векторов симметрической матрицы, будет основываться на следующей теореме.
□ Теорема 3.21.
Каждую
симметрическую матрицу
можно при помощи ортогональной матрицы
![]() привести к диагональному виду
привести к диагональному виду
![]() .
.
Доказательство
проведем
методом математической индукции по
порядку матрицы
.
Если матрица
имеет порядок, равный единице, т. е.
![]() ,
то она уже является диагональной. Далее,
единичная матрица
,
то она уже является диагональной. Далее,
единичная матрица
![]() первого порядка, т. е.
первого порядка, т. е.
![]() ,
обратима и обратная матрица имеет вид
,
обратима и обратная матрица имеет вид
![]() .
Обе эти матрицы являются ортогональными.
Наконец, из матричного равенства
.
Обе эти матрицы являются ортогональными.
Наконец, из матричного равенства
![]() следует, что
следует, что
![]() .
.
Пусть теперь
утверждение теоремы справедливо для
всех симметрических матриц, порядок
которых равен
.
Докажем теорему для симметрической
матрицы
порядка
.
Из теоремы 3.20 следует, что матрица
имеет собственное значение
.
Возьмем в подпространстве
ненулевой вектор и нормируем его.
Полученный вектор обозначим символом
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Дополним нормированный вектор
до ортонормированного базиса
.
Дополним нормированный вектор
до ортонормированного базиса
![]() пространства
и рассмотрим ортогональную матрицу
пространства
и рассмотрим ортогональную матрицу
![]() ,
столбцами которой являются координаты
векторов этого ортонормированного
базиса. Теперь для первого столбца
матрицы
,
столбцами которой являются координаты
векторов этого ортонормированного
базиса. Теперь для первого столбца
матрицы
![]() получим следующее выражение:
получим следующее выражение:
![]() .
.
Отсюда следует, что матрица может быть записана в виде
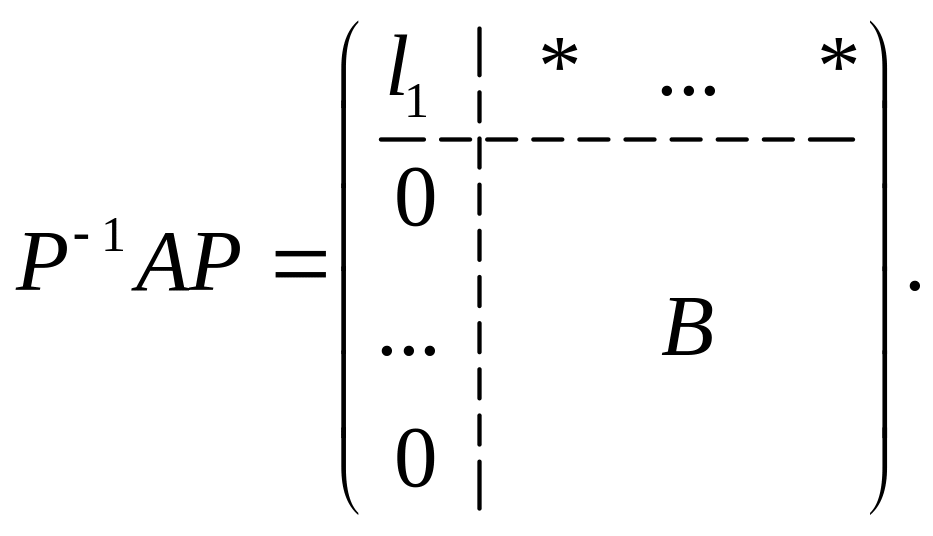
Так как матрица симметрическая (теорема 3.19), то все элементы этой матрицы, расположенные в первой строке, за исключением быть может , равны нулю. Итак
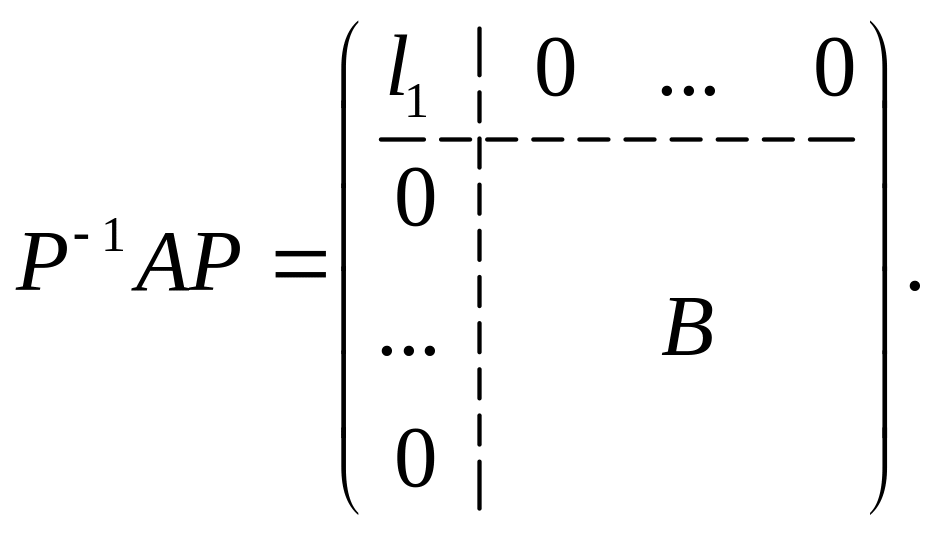
Из леммы 1 вытекает, что
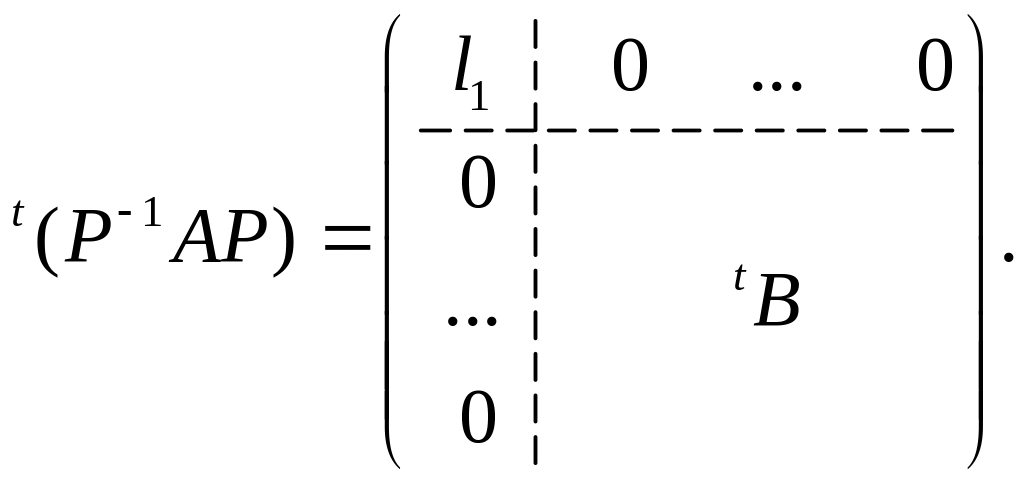
Из симметричности
матрицы
вытекает равенство
![]() .
Отсюда следует, что
.
Отсюда следует, что
![]() и, значит,
и, значит,
![]() симметрическая
матрица.
симметрическая
матрица.
Симметрическая матрица имеет порядок и, по предположению индукции, найдется такая ортогональная матрица , что
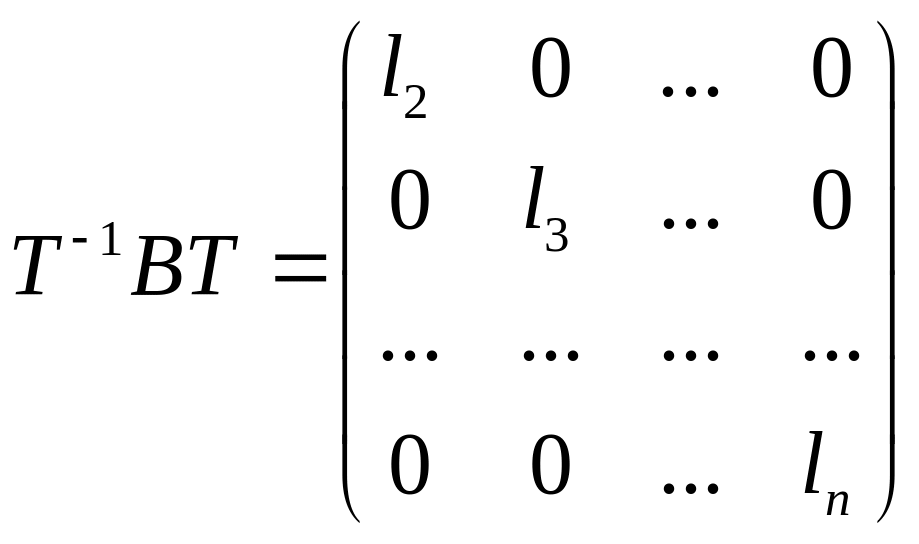 .
.
Из леммы 2 следует ортогональность матрицы
,
а из леммы 1 вытекает, что матрица обратима и

Теперь обозначим
произведение ортогональных матриц
и
символом
,
т. е.
![]() .
Из теоремы 3.17 следует, что
– ортогональная матрица. Используя
лемму 1, получим следующую цепочку
равенств:
.
Из теоремы 3.17 следует, что
– ортогональная матрица. Используя
лемму 1, получим следующую цепочку
равенств:
![]()
=

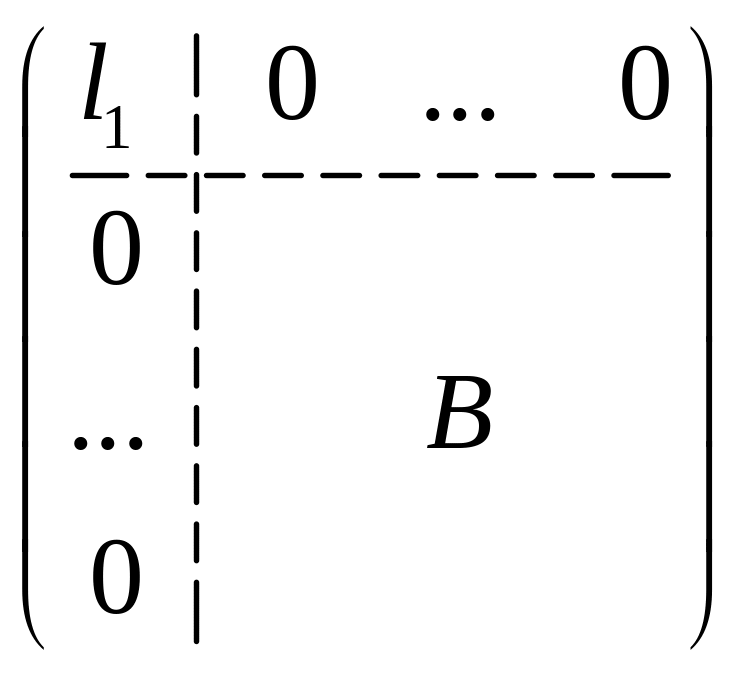
 =
=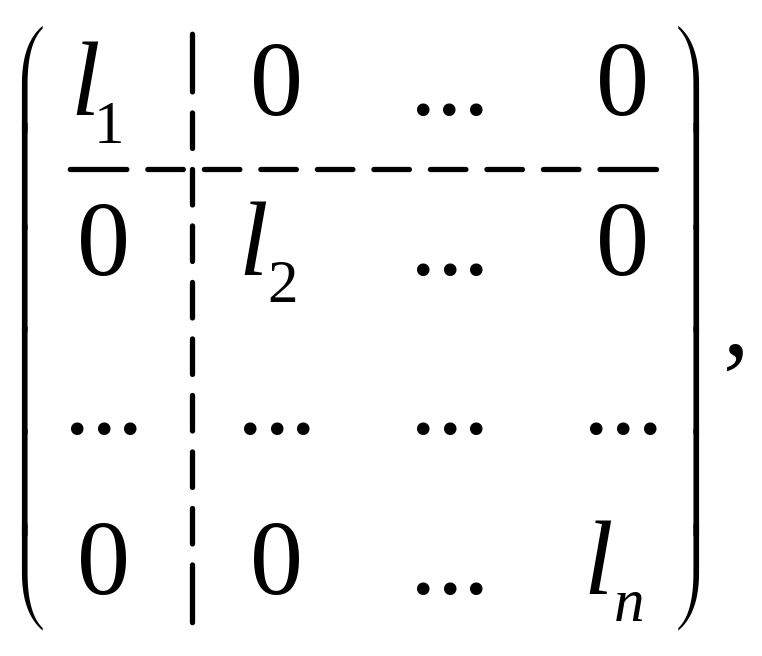
т. е. ортогональная матрица приводит матрицу к диагональному виду. ■
Теперь доказанная теорема 3.21 позволяет построить в пространстве Rn ортонормированный базис, состоящий из собственных векторов симметрического преобразования .
□ Теорема 3.22.
Пусть
![]() все различные собственные значения
симметрической матрицы
.
Тогда объединение ортонормированных
базисов подпространств
все различные собственные значения
симметрической матрицы
.
Тогда объединение ортонормированных
базисов подпространств
![]()
![]() является ортонормированным базисом
пространства
.
является ортонормированным базисом
пространства
.
Доказательство.
В каждом подпространстве
![]() выберем ортонормированный базис. Из
теорем 3.21 и 3.11 следует, что объединенная
система этих базисов
выберем ортонормированный базис. Из
теорем 3.21 и 3.11 следует, что объединенная
система этих базисов
![]() является базисом Rn.
В силу построения векторы
является базисом Rn.
В силу построения векторы
![]() нормированы. Докажем ортогональность
этой системы векторов.
нормированы. Докажем ортогональность
этой системы векторов.
Пусть
и
– произвольные различные векторы
системы
.
Если они лежат в одном подпространстве
![]() то они принадлежат ортонормированному
базису этого подпространства и, значит,
ортогональны. Пусть теперь
то они принадлежат ортонормированному
базису этого подпространства и, значит,
ортогональны. Пусть теперь
![]() и
и
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
Отсюда следует
![]() ,
,
![]()
Из симметричности матрицы вытекает равенство левых частей этих равенств и, значит, равны их правые части
![]() .
.
Так как собственные
значения
и
![]() различны, то
различны, то
![]() и, значит,
и, значит,
![]() ■
■
Алгоритм построения ортонормированного базиса пространства , состоящего из собственных векторов симметрической матрицы .
1. Найти собственные значения матрицы .
2. Для каждого
собственного значения
найти фундаментальный набор решений
системы уравнений
![]() ,
т. е. найти базис подпространства
.
,
т. е. найти базис подпространства
.
3. Ортогонализировать и нормировать найденные базисы под-пространств.
4. Объединить ортонормированные базисы подпространств .
Пример
Найти ортонормированный
базис пространства
![]() состоящий из собственных векторов
матрицы
состоящий из собственных векторов
матрицы
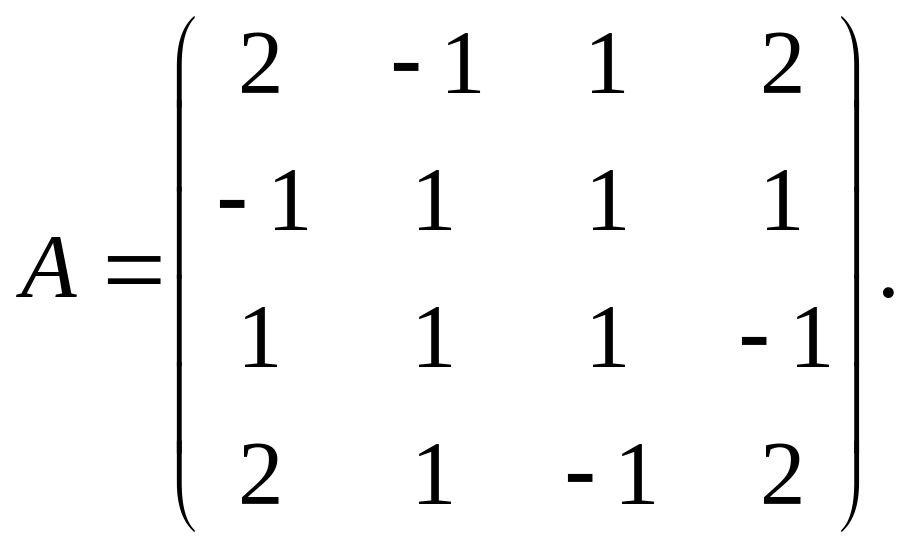
Решение. Сначала найдем характеристический многочлен матрицы

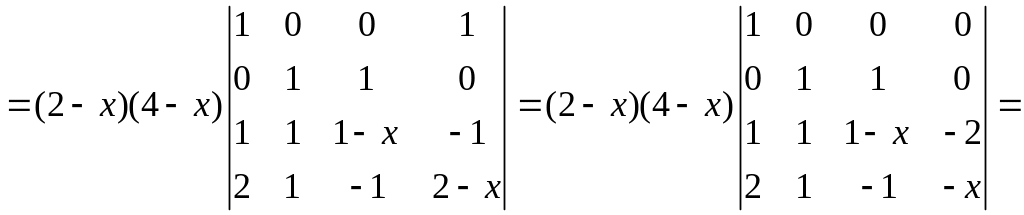
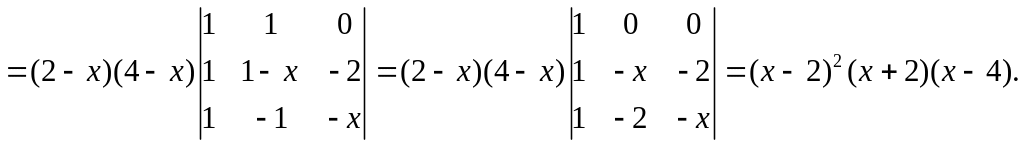
Собственные значения матрицы равны 2, 2 и 4.
Теперь надо найти
базисы подпространств
![]() ,
и
,
и
![]() ,
т. е. найти фундаментальные наборы
решений систем уравнений:
,
т. е. найти фундаментальные наборы
решений систем уравнений:
![]() ,
и
,
и
![]() Базис подпространства
состоит из одного вектора
Базис подпространства
состоит из одного вектора
![]() ,
базис A(2)
образуют векторы
,
базис A(2)
образуют векторы
![]() ,
,
![]() и базис подпространства
состоит из одного вектора
и базис подпространства
состоит из одного вектора
![]() .
.
Базис подпространства
не является ортогональным. После его
ортогонализации и объединения базисов
всех подпространств получим
ортонормированный базис пространства
![]() ,
состоящий из собственных векторов
матрицы
:
,
состоящий из собственных векторов
матрицы
:
![]() .
.
Задачи
1. Доказать, что
для любой матрицы
матрица
![]() – симметрическая матрица.
– симметрическая матрица.
2. Доказать, что
для любой обратимой матрицы
матрица
![]() будет симметрической тогда и только
тогда, когда симметрической будет
матрица
.
будет симметрической тогда и только
тогда, когда симметрической будет
матрица
.
3. Доказать, что
если
и
− симметрические матрицы, то матрицы
и
![]() также симметрические.
также симметрические.
4. Доказать, что
симметрические матрицы
и
перестановочны тогда и только тогда,
когда
![]() симметрическая матрица.
симметрическая матрица.
5. Доказать, что
матрица
cимметрическая,
если матрица
ортогональная и
![]() =
Е.
=
Е.
6. Доказать, что матрица симметрическая, если в пространстве имеется ортонормированный базис, состоящий из собственных векторов матрицы .
Найти ортонормированный
базис пространства R![]() ,
состоящий из собственных векторов
симметрической матрицы.
,
состоящий из собственных векторов
симметрической матрицы.
7.
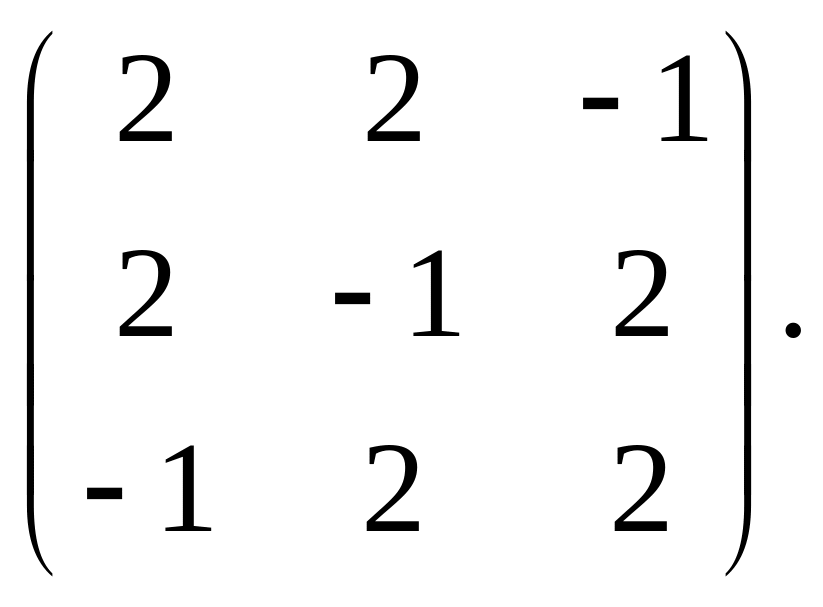 8.
8.
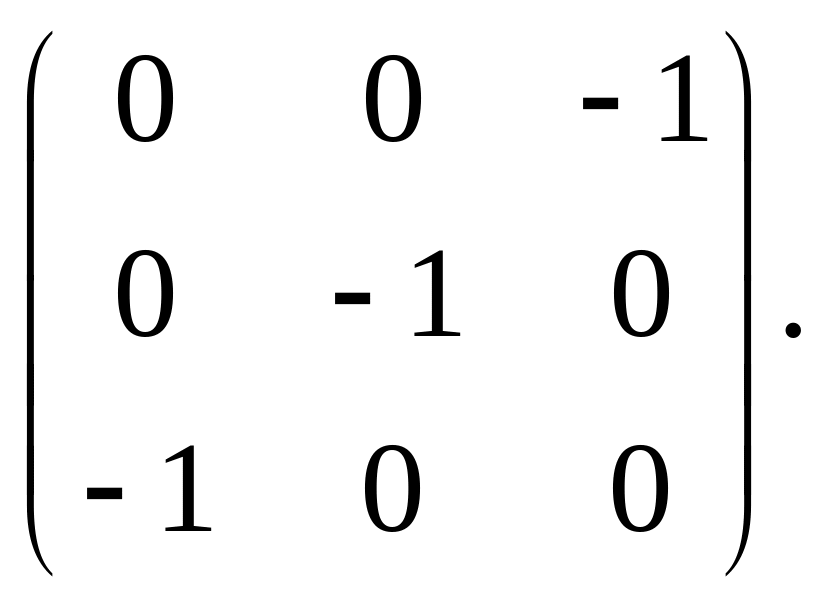 9.
9.
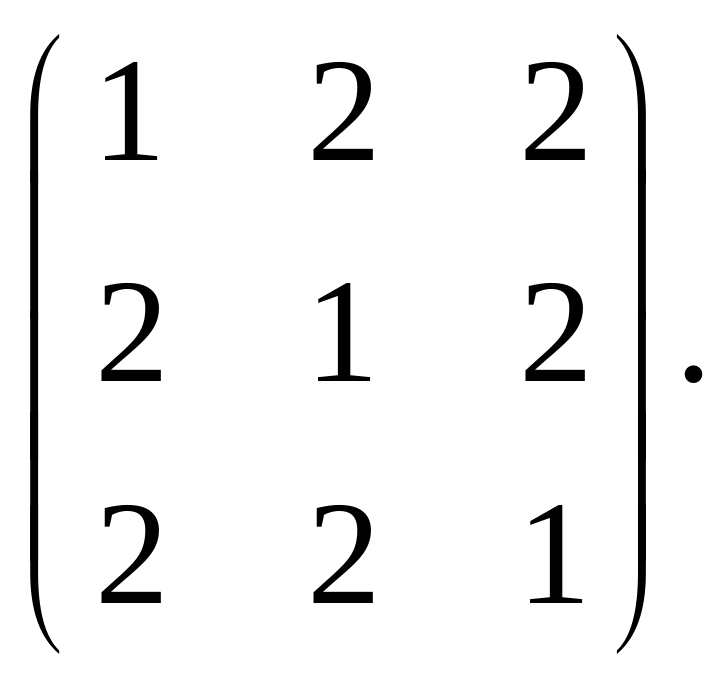
Найти ортогональную матрицу, которая приводит симметрическую матрицу к диагональному виду, написать этот диагональный вид.
10.
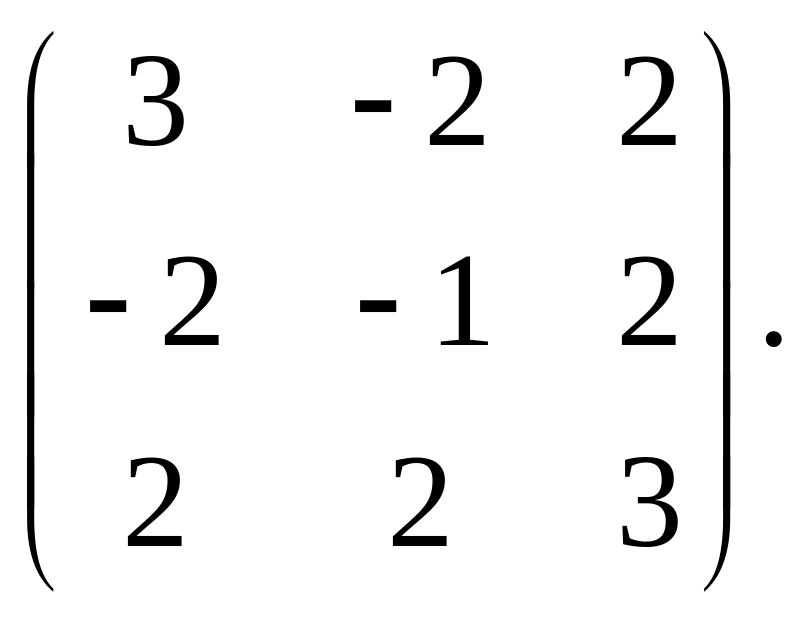 11.
11.
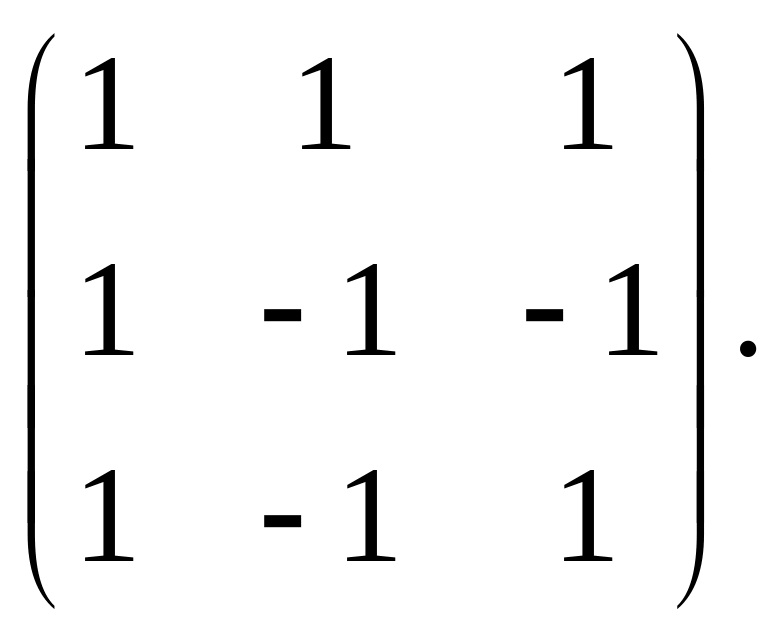 12.
12.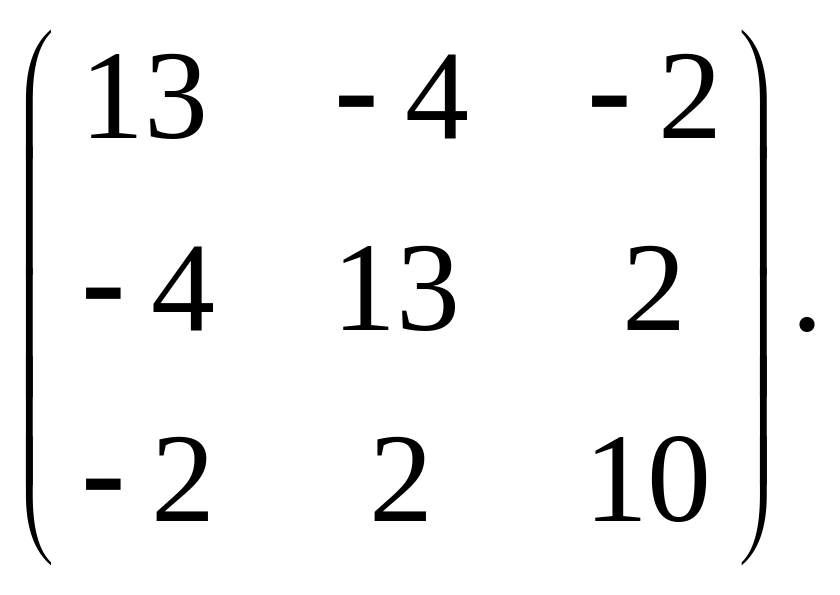
13. Найти все диагональные матрицы, к которым приводится при помощи ортогональной матрицы симметрическая матрица
![]()
![]()
![]()
![]() .
.
