Спектральное разложение стационарного с.П.

Существует связь между характером корреляционной функции и внутренней структурой соответствующего ей с.п.

Спектром колебательного процесса называется функция, описывающая распределение амплитуд по частотам. Для с.п. амплитуда является случайной величиной, соответственно спектр с.п. будет описывать распределение дисперсии по различным частотам, а спектральное разложение функции – представление её в виде суммы гармонических колебаний, имеющих различные амплитуды и частоты.

Рассмотрим с.п. X(t) на конечном интервале (0, T).

K_x(τ)

τ = t₂ – t₁

0 < t₂ < T

0 < t₁ < T

-T < t₂ – t₁ < T

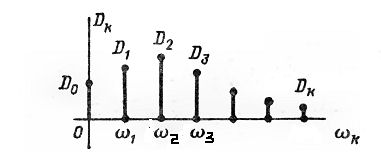
Разложим корреляционную функцию K_x(τ) на промежутке (0, Т) в ряд Фурье по четным гармоникам (по cos):

(*)

ω_k = k ω₁ ; ω₁ = π / T

,

Если функция четная, то выполняется

,

- каноническое разложение по координатным функциям cosωt и sinωt.

, где

U_k, V_k – не коррелированные центрированные с.в. с дисперсиями D_k.

Такое разложение называется спектральным разложением.

D[U_k] = D[V_k] = D_k.

Спектральное разложение на бесконечном участке времени.

Чем больше участок Т, тем полнее сведения о с.п.

Если Т →∞, то Δω →0.

Введем в рассмотрение среднюю плотность дисперсии, т.е. дисперсию приходящуюся на единицу длины данного интервала частот:

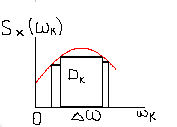
D_k = S_x(ω_k)Δω

Суммарная площадь всей диаграммы – это дисперсия D_x.

, спектральная плотность стационарного с.п. X(t).

В этом случае выражение (*) примет вид:

Таким образом корреляционная функция и спектральная плотность стационарного с.п. связаны между собой косинус-преобразованием Фурье. Следовательно, спектральная плотность выражается через корреляционную функцию стационарного с.п. следующим образом:

при T→∞, ω_k→ω, ∆ω→0, ∑→∫.

Свойства спектральной плотности S_x(ω):

1. S_x(ω) – неотрицательная функция, т.е. S_x(ω) ≥ 0;

2. Дисперсия выражается через спектральную плотность:

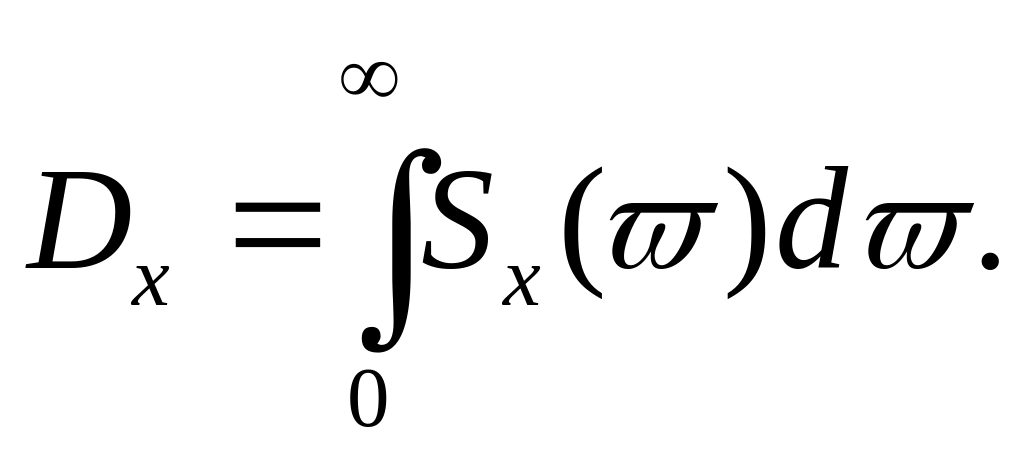
Нормированная спектральная плотность:

.

Нормированная к.ф. и нормированная спектральная плотность связаны между собой преобразованием Фурье:

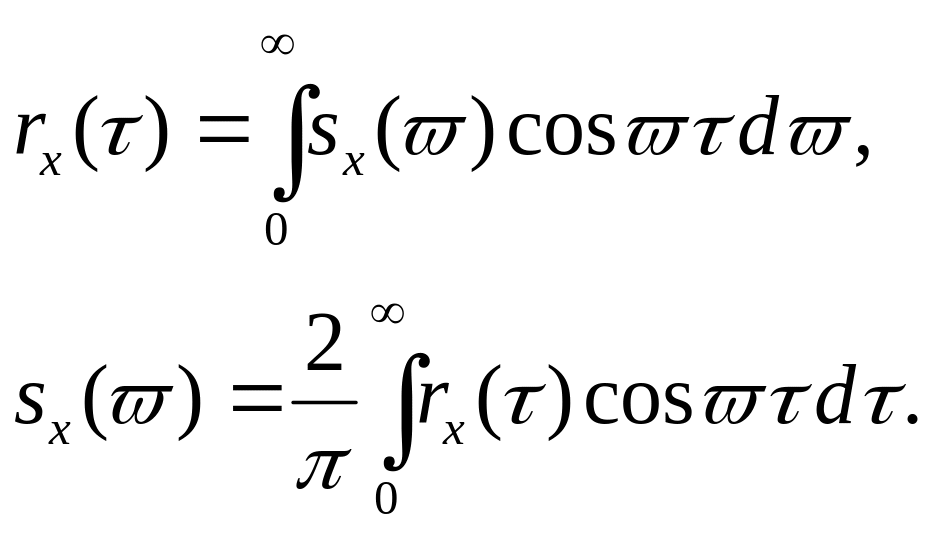
Комплексная спектральная плотность:

С помощью формул Эйлера для комплексных чисел

e^iz = cosz + i sin z, e^-iz = cosz - i sin z, где - мнимая единица, элементарный с.п. X(t) может быть записан в виде

Обозначим :

(*)

Покажем, что выражение (*) представляет собой каноническое разложение элементарного с.п. в комплексной форме:

т.к. M[V_k] = M[U_k] = 0

Аналогично получим:

Покажем что с.в. не коррелированы:

т.к.

Найдем дисперсию с.в.

Аналогично,

Введем в рассмотрение новую функцию , которую определим следующим образом:

=S_x(ω)/2 при ω ≥ 0, (**)

=S_x(-ω)/2 при ω < 0.

Таким образом функция является четной функцией аргумента ω и определена для любых значений этого аргумента – как положительных, так и отрицательных.

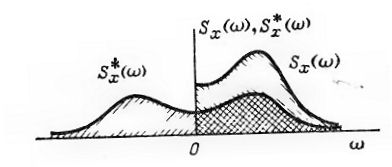
На рисунке показаны графики функций S_x(ω) и . Значения функции при положительных значениях ω в два раза меньше значений спектральной плотности S_x(ω) при тех же значениях аргумента ω.

Функция называется спектральной плотностью стационарного случайного процесса в комплексной форме. Она обладает тремя свойствами:

1. ≥ 0 при -∞ < ω < ∞;

2. ;

3. = .

С учетом (**) выражение для K_x(τ) примет вид:

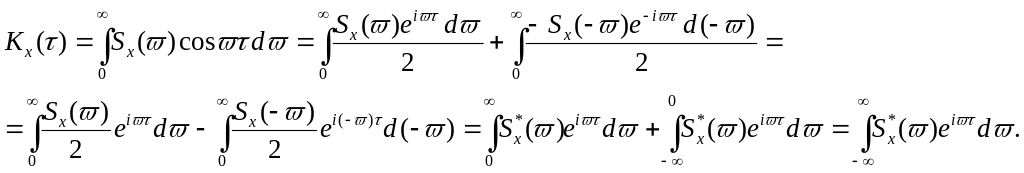
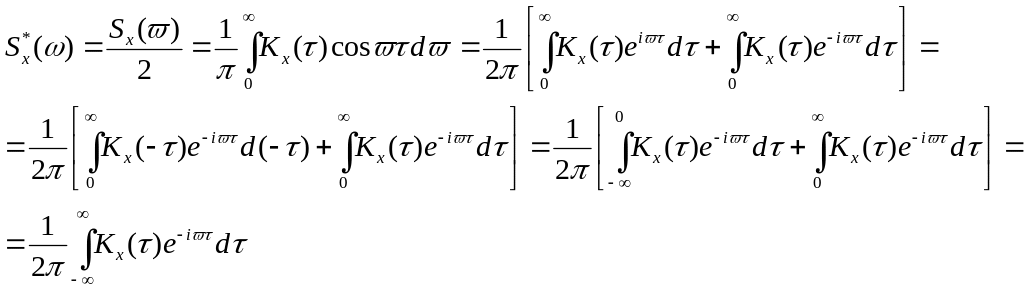
Два случайных процесса называются стационарно-связанными, если их взаимная корреляционная функция зависит только от τ.

R_xy(t₁,t₂) = R_xy(τ), τ = t₂ – t₁;

R_xy(τ) = R_yx(-τ)

R_xy(t₂ – t₁) = R_yx(t₁ – t₂) = R_xy(-τ)

Взаимная спектральная плотность

Линейные преобразования стационарных случайных процессов

Дифференцирование

,

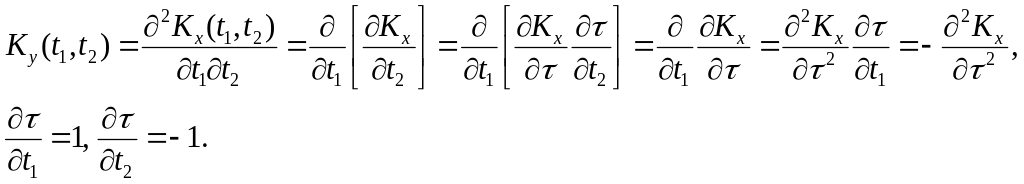
Взаимная корреляционная функция производной и самого процесса

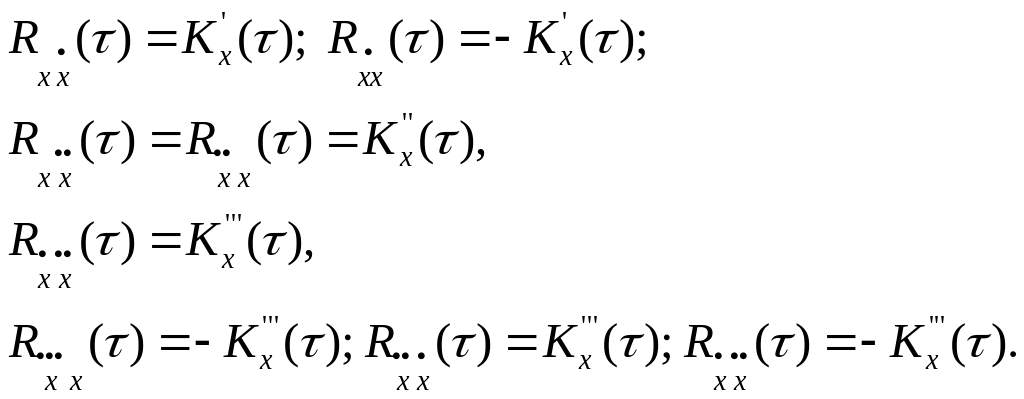
Стационарный процесс стационарно связан со своей производной

Дельта функция

Дельта-функция δ(t) – предел последовательности однопараметрического семейства непрерывных функций. Дельта-функцию определяют тем условием, что она ставит в соответствие всякой непрерывной функции её значение при t = 0:

Дельта-функция представима интегралом Фурье:

Отсюда

В приложениях часто используют соотношение

Преобразование стационарного с.п.

стационарной линейной динамической системы

Стационарной линейной динамической системой называют устройство, которое описывается линейным дифференциальным уравнением с постоянными коэффициентами вида

a_nY⁽ⁿ⁾(t)+a_n-1Y^(n-1)(t)+...+a₀Y(t) = b₀X(t)+b₁X⁽¹⁾(t)+...+b_mX^m(t) ,

где X (t) - входная стационарная случайная функция (воздействие, возмущение), Y (t)—выходная случайная функция (реакция, отклик).

Оператор дифференцирования:

(a_npⁿ+a_n-1p^n-1+ ... +a₀)Y(t)= (b_mp^m+b_m-1p+ ... +b₀)X(t).

,

A_n(p)Y(t) = B_m(p)X(t)

, Φ(p) – передаточная функция.

Будем решать дифференциальное уравнение:

Решение в виде: Y₁(t) + Y₂(t)

Y₁(t) – собственные колебания системы при отсутствии входного воздействия.

Y₂(t) – вынужденные колебания системы под воздействием сигнала.

1.

Будем искать реакцию системы Y(t) в виде простого гармонического колебания, но умноженного на некоторый комплексный множитель:

, тогда

,

разделим обе части на , получим:

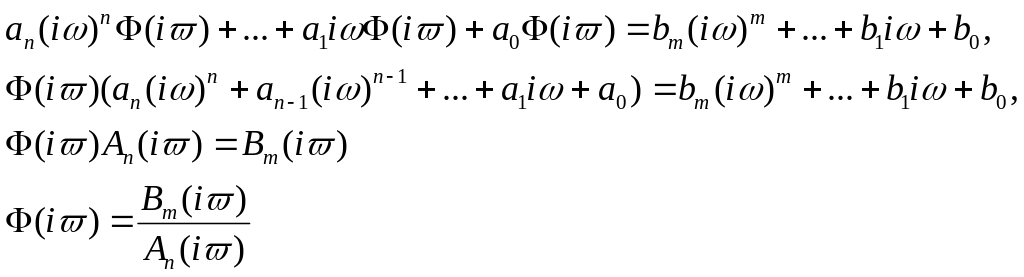
Если на вход линейной динамической системы поступает гармоническое колебание вида , то реакция системы представляется в виде того же гармонического колебания, умноженного на частотную характеристику.

2.

Реакция системы на сумму воздействий равна сумме реакций на отдельные воздействия.

если , то

Определим спектр для полученного разложения:

При преобразовании стационарного с.п. стационарной линейной динамической системы каждая из ординат его спектра умножается на квадрат модуля частотной характеристики системы для соответствующей частоты.

Определим спектральную плотность:

Спектральная плотность стационарного с.п. Y(t) на выходе стационарной линейной системы равна произведению спектральной плотности стационарного с.п. X(t), подаваемого на вход системы, на квадрат модуля частотной характеристики этой системы.

Определим математическое ожидание.

Математическое ожидание будем рассматривать как колебание в нулевой момент времени, т.е. будем рассматривать колебание нулевой частоты:

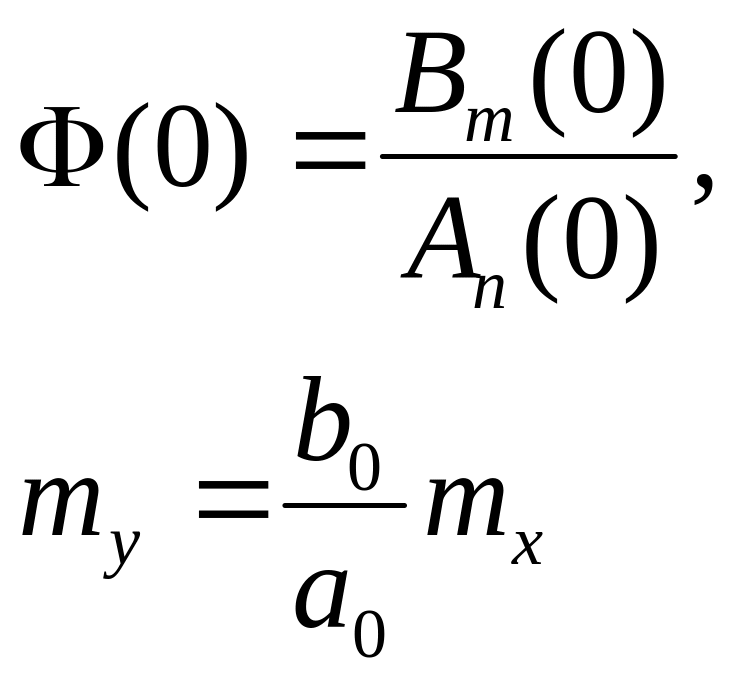
Алгоритм:

Дано: X(t), m_x(t), K_x(t₁, t₂)

1. ;

2. ;

3. ;

4. ;

5. .