
- •Гаврилов в.Л. Функции нескольких переменных
- •Евклидово -мерное пространство
- •Окрестности. Области
- •Функции нескольких переменных
- •Предел функции нескольких переменных
- •Непрерывность функции нескольких переменных
- •Решение задач
- •Вопросы для самопроверки по теме 8.1
- •Тесты для самопроверки по теме 8.1
- •Ответы на тесты по теме 8.1
- •8.2. Дифференцирование функций нескольких переменных
- •Частные производные
- •Дифференцируемость функции нескольких переменных
- •Полный дифференциал
- •Дифференцирование сложной функции одной переменной. Полная производная
- •Дифференцирование сложной функции нескольких переменных. Инвариантность формы полного дифференциала
- •Тогда функция
- •Дифференцирование неявных функций
- •В нашем случае
- •Частные производные высших порядков
- •Полные дифференциалы высших порядков
- •Рассмотрим функцию
- •Аналогично предыдущему можно показать, что
- •Решение задач
Непрерывность функции нескольких переменных
Для
функции нескольких переменных (как и
для функции одной
переменной) с понятием предела тесно
связано понятие непрерывности.
Пусть функция
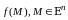 определена в некоторой
окрестности конечной точки
включая
и саму эту точку. Символом
определена в некоторой
окрестности конечной точки
включая
и саму эту точку. Символом
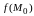 обозначается значение функции
в точке
обозначается значение функции
в точке
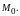
Определение.
Функция
называется непрерывной
в
точке
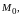 если
если
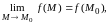 (8.2)
(8.2)
причем точка стремится к точке произвольным образом, оставаясь в области определения функции.
Равенство (8.2) означает, что предел функции в точке существует, конечен и его величина совпадает со значением функции в этой точке.
Рассмотрим
разность
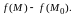 Назовем ее полным
приращением
функции
в точке
и
обозначим
Назовем ее полным
приращением
функции
в точке
и
обозначим
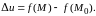 (8.3)
(8.3)
Пусть
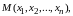
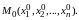 Обозначим
Обозначим
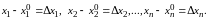 (8.4)
(8.4)
Используя
эти обозначения, получим для полного
приращения
функции
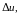 соответствующего приращениям аргументов
соответствующего приращениям аргументов
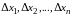 ,
следующее выражение:
,
следующее выражение:
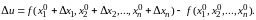 (8.5)
(8.5)
Очевидно, что
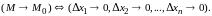 (8.6)
(8.6)
Теорема.
Для
того чтобы функция
была непрерывна
в точке
необходимо
и достаточно, чтобы полное приращение
функции
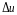 стремилось к нулю при стремлении к нулю
вызвавших его приращений аргументов.
стремилось к нулю при стремлении к нулю
вызвавших его приращений аргументов.
Эта теорема позволяет дать другое определение непрерывности функции в точке, равносильное приведенному.
Определение. Функция называется непрерывной в точке если в этой точке ее полное приращение стремится к нулю при стремлении к нулю приращений аргументов, вызвавших это приращение.
Следуя этому определению можно сказать, что непрерывна в некоторой точке, если малые изменения координат (приращений аргументов) вызывают сколь угодно малое изменение значений самой функции.
Определение.
Функция
 называется непрерывной
в области
называется непрерывной
в области
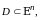 если
она непрерывна в каждой
точке этой области.
если
она непрерывна в каждой
точке этой области.
Если в какой-то точке функция не является непрерывной, то говорят, что функция в этой точке терпит разрыв.
Точки разрыва могут быть изолированными или образовывать линии разрыва, поверхности разрыва и так далее.
Пример. Найти точки разрыва функции

Решение.
Функция
определена и непрерывна во всех точках
плоскости
кроме
точек, координаты которых удовлетворяют
уравнению
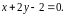 Это уравнение прямой. Каждая
точка прямой есть точка разрыва; все
они образуют линию разрыва.
Это уравнение прямой. Каждая
точка прямой есть точка разрыва; все
они образуют линию разрыва.
Непрерывные функции нескольких переменных обладают, по существу, теми же свойствами, что и непрерывные функции одной переменной. Сформулируем теорему о непрерывных функциях.
Теорема. Если функции и непрерывны в точке то в этой точке непрерывны и функции


(последняя
при условии, что
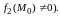
Аналогом замкнутого промежутка для функции одной переменной, для функции нескольких переменных служит ограниченная замкнутая область.
Если функция непрерывна в ограниченной замкнутой области, то в этой области она ограничена; среди ее значений есть наибольшее и наименьшее; она принимает все значения от наименьшего до наибольшего.
Решение задач
Задача
1.
Найти значение функции
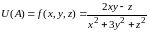 в точке
в точке
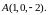
Решение.
Подставляя
в выражение функции
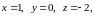 получим
получим
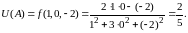 Задача
2.
Найти
Задача
2.
Найти
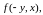 если
если
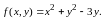
Решение.
Выражение
 получим,
заменяя
получим,
заменяя
 на
на
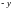 и
и
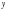 на
на
 :
:

Задача
3.
Найти и изобразить на рисунке область
определения функции
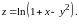
Решение.
Логарифм
определен только при положительных
значениях
его аргумента, поэтому область определения
функции
определяется неравенством
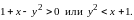
Уравнение
границы области
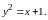 Это уравнение параболы, вершина которой
находится в точке
Это уравнение параболы, вершина которой
находится в точке
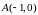 ,
а ветви направлены в положительную
сторону оси
.
Ось
,
а ветви направлены в положительную
сторону оси
.
Ось
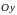 парабола пересекает в точках
парабола пересекает в точках
 и
и
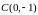 .
.
Парабола
делит плоскость на две части – внутреннюю
и внешнюю по отношению к параболе. Для
точек одной из частей выполняется
неравенство
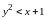 ,
а для другой
,
а для другой
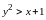 .
.
Чтобы определить, какая часть является областью , т.е. где выполняется условие , нужно проверить выполнение этого условия для какой-нибудь одной точки, не лежащей на параболе.
Возьмем
для простоты точку
 .
Она лежит “внутри” параболы. Для нее
удовлетворяется нужное условие
.
Она лежит “внутри” параболы. Для нее
удовлетворяется нужное условие
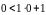 .
Следовательно, точка
принадлежит области определения
и вся область состоит из внутренних
“точек” параболы (заштрихована). Сама
парабола (рис. 8.7)в область
не входит (изображена пунктиром).
.
Следовательно, точка
принадлежит области определения
и вся область состоит из внутренних
“точек” параболы (заштрихована). Сама
парабола (рис. 8.7)в область
не входит (изображена пунктиром).
Задача
4.
Найти область определения функции
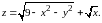 Определить, будет ли она ограниченным,
замкнутым, односвязным множеством.
Определить, будет ли она ограниченным,
замкнутым, односвязным множеством.
Решение.
Корень
квадратный определен только для
неотрицательных значений аргумента.
Следовательно, для координат точек
области определения функции должны
выполняться условия:
 и
и
 или
или
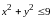 и
.
и
.
Первое неравенство выполняется для точек, лежащих на окружности с центром в начале координат и радиусом, равным 3, и точек, лежащих внутри окружности. Второе неравенство верно для точек оси и точек, лежащих в правой полуплоскости.
Одновременно условия выполняются в точках правого полукруга и на его границах (правая часть полуокружности и отрезок ). Очевидно, что множество точек определения функции – ограниченное, замкнутое и односвязное (ограниченная замкнутая область).
Задача
5.
Найти точки разрыва функции
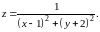
Решение.
Данная
функция может иметь разрывы только в
точках, где знаменатель равен нулю.
Уравнение
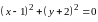 имеет одно решение
имеет одно решение
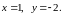 Точка
Точка
 - точка разрыва функции.
- точка разрыва функции.
Задача
6.
Исследовать на непрерывность функцию
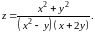
Решение.
Эта
функция может иметь разрывы только в
точках, где знаменатель обращается в
нуль. Решая уравнение
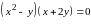 относительно
,
получаем
относительно
,
получаем
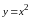 и
и
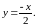 Следовательно, точками разрыва будут
точки параболы
и точки прямой
Следовательно, точками разрыва будут
точки параболы
и точки прямой
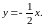 Функция имеет две линии разрыва.
Функция имеет две линии разрыва.
