- •Гаврилов в.Л. Функции нескольких переменных
- •Евклидово -мерное пространство
- •Окрестности. Области
- •Функции нескольких переменных
- •Предел функции нескольких переменных
- •Непрерывность функции нескольких переменных
- •Решение задач
- •Вопросы для самопроверки по теме 8.1
- •Тесты для самопроверки по теме 8.1
- •Ответы на тесты по теме 8.1
- •8.2. Дифференцирование функций нескольких переменных
- •Частные производные
- •Дифференцируемость функции нескольких переменных
- •Полный дифференциал
- •Дифференцирование сложной функции одной переменной. Полная производная
- •Дифференцирование сложной функции нескольких переменных. Инвариантность формы полного дифференциала
- •Тогда функция
- •Дифференцирование неявных функций
- •В нашем случае
- •Частные производные высших порядков
- •Полные дифференциалы высших порядков
- •Рассмотрим функцию
- •Аналогично предыдущему можно показать, что
- •Решение задач
В нашем случае
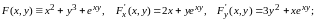
следовательно,

Неявным образом могут быть заданы функции двух и более переменных.
Если
неявная функция двух переменных
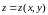 определяется уравнением
определяется уравнением
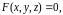
то частные производные и этой функции можно найти по следующим формулам
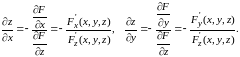 (8.20)
(8.20)
Пример.
Найти
полный дифференциал функции
,
заданной
неявно уравнением

Решение. Полный дифференциал функции вычисляется по формуле
Найдем
и
по формулам (8.20). Для этого перенесем
все члены
уравнения в левую часть и обозначим
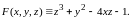 Так
как
Так
как

то
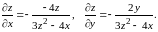
Теперь
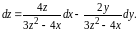
Частные производные высших порядков
Частные
производные
 и
и
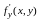 функции
называемые частными
производными первого порядка,
в
свою очередь, будут некоторыми функциями
переменных
и
.
Если последние сами обладают частными
производными,
то эти частные производные называются
частными
производными
второго порядка для функции
.
При
этом используют
обозначения:
функции
называемые частными
производными первого порядка,
в
свою очередь, будут некоторыми функциями
переменных
и
.
Если последние сами обладают частными
производными,
то эти частные производные называются
частными
производными
второго порядка для функции
.
При
этом используют
обозначения:

Частные
производные от частных производных
второго порядка
называются частными
производными третьего порядка.
Вообще,
если некоторая функция
допускает
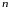 -кратное
частное дифференцирование по своим
аргументам в каком-либо
определенном порядке, то получается
частная
производная
-го
порядка.
Например,
-кратное
частное дифференцирование по своим
аргументам в каком-либо
определенном порядке, то получается
частная
производная
-го
порядка.
Например,
 обозначает результат
-кратного
последовательного дифференцирования
функции
по аргументу
,
то есть частную производную
-го
порядка от
по
.
обозначает результат
-кратного
последовательного дифференцирования
функции
по аргументу
,
то есть частную производную
-го
порядка от
по
.
Частная производная, полученная дифференцированием по нескольким различным аргументам, называется смешанной частной производной.
Всего
указанным образом можно получить
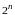 частных производных
порядка
от функции
.
В
действительности, число различных
производных какого-либо определенного
порядка оказывается
значительно меньше. Справедлива следующая
важная теорема
о смешанных частных производных.
частных производных
порядка
от функции
.
В
действительности, число различных
производных какого-либо определенного
порядка оказывается
значительно меньше. Справедлива следующая
важная теорема
о смешанных частных производных.
Теорема.
Если функция
обладает в некоторой
точке непрерывными частными производными
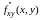 и
и
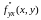 ,
то эти производные равны одна другой в
рассматриваемой точке:
,
то эти производные равны одна другой в
рассматриваемой точке:
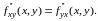
Аналогичная
теорема о независимости смешанной
частной
производной от порядка дифференцирования
справедлива
для частных производных любого порядка.
Поэтому обозначение
частной производной для таких функций
указывает только число
дифференцирований по каждой переменной,
а порядок, в котором
производятся эти дифференцирования,
на результат не влияет.
Так, через
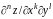 обозначается частная производная
порядка
для функции
,
причем
по
выполняется
дифференцирование
обозначается частная производная
порядка
для функции
,
причем
по
выполняется
дифференцирование
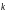 раз, а по
раз, а по
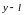 раз (здесь, конечно,
раз (здесь, конечно,
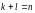 ).
).
Сказанное
справедливо и для функции произвольного
числа аргументов. Например, для функции
трех аргументов
через
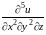 обозначается частная производная пятого
порядка,
получаемая двукратным дифференцированием
по
,
двукратным
- по
обозначается частная производная пятого
порядка,
получаемая двукратным дифференцированием
по
,
двукратным
- по
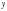 и
однократным – по
.
и
однократным – по
.
Пример
1. Найти
вторые частные производные функции
 Убедиться, что
Убедиться, что
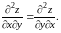
Решение. Находим сначала частные производные
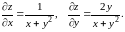
Дифференцируя каждую из полученных производных по и по , получим вторые частные производные
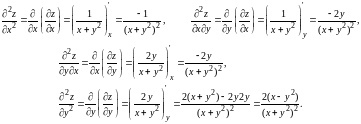
Очевидно, что смешанные производные равны.
Пример
2. Найти
 если
если
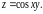
Решение. Находим сначала частную производную по
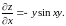
Далее ищем вторую частную производную по
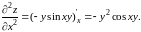
Теперь