20. Раскрытие неопределенности по правилу Лопиталя.

Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.

Итак, если имеется неопределенность вида или , то .

Доказательство. Рассмотрим доказательство теоремы для неопределенности вида при .

Для простоты будем предполагать, что функции и , а также их производные непрерывны в точке , причем и . В этом случае .

Применяя теорему Лагранжа для функций и на отрезке , получим , где , .

При в силу непрерывности производных и имеем и . Используя теорему о пределе частного получаем равенство .

Пример. Раскрыть неопределенность по правилу Лопиталя и найти предел функции: .

.

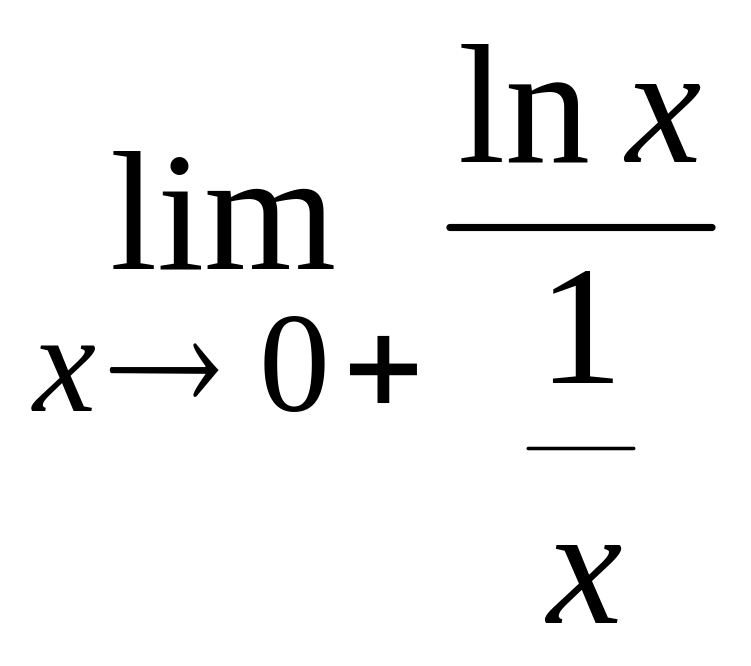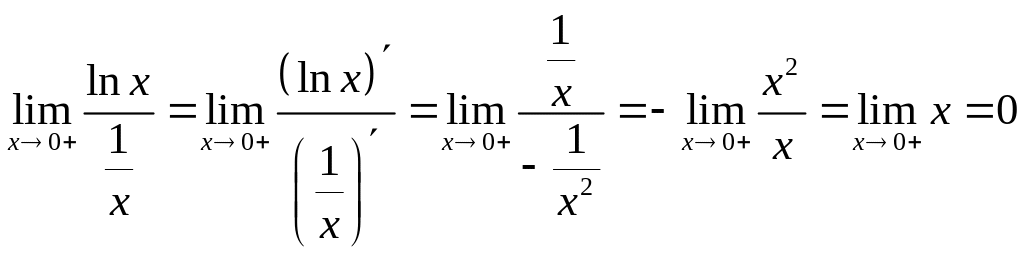21.Экстремум функции, точки перегиба, асимптоты.

Определение. Точка называется точкой максимума функции , если в некоторой окрестности точки выполняется неравенство .

Определение. Точка называется точкой минимума функции , если в некоторой окрестности точки выполняется неравенство .

Теорема. Для того чтобы функция имела экстремум в точке , необходимо и достаточно, чтобы ее производная в этой точке равнялась нулю или не существовала.

Теорема. Если при переходе через точку производная дифференцируемой функции меняет свой знак с плюса на минус, то точка есть точка максимума функции , а если с минуса на плюс, - то точка минимума.

Теорема. Если первая производная дважды дифференцируемой функции равна нулю в некоторой точке , а вторая производная в этой точке положительна, то есть точка минимума функции ; если отрицательна, то - точка максимума.

Определение. Функция называется выпуклой вниз на промежутке Х, если для любых двух значений , из этого промежутка выполняется неравенство .

Определение. Функция называется выпуклой вверх на промежутке Х, если для любых двух значений , из этого промежутка выполняется неравенство .

Определение. Точкой перегиба графика непрерывной функции называется точка, разделяющая интервал, в которых функция выпукла вниз и вверх.

Теорема. Вторая производная дважды дифференцируемой в точке перегиба равна нулю, т.е. .

Теорема. Если вторая производная дважды дифференцируемой функции при переходе через некоторую точку меняет свой знак, то есть точка перегиба ее графика.

Прямая линия называется асимптотой графика функции , если расстояние от точки , лежащей на графике, до этой прямой стремится к нулю при движении точки по графику в бесконечность.

Прямая называется вертикальной асимптотой графика функции , если хотя бы одно из предельных значений или равно или .

Прямая называется горизонтальной асимптотой графика функции при , если .

Прямая называется наклонной асимптотой графика функции при , если функцию можно представить в виде , где при .

Теорема. Для того чтобы функция имела при наклонную асимптоту , необходимо и достаточно, чтобы существовали два предела и .

Пример. Найти асимптоты функции .

Вертикальная асимптота пересекает ось абсцисс в точке , , т.к. , , , .

Так как , то горизонтальных асимптот функция не имеет. Найдем наклонные асимптоты: ,

. Прямая - наклонная асимптота.