3.2. Опис лінійних дискретних систем у часі

Задача опис лінійних дискретних систем у часі полягає у встановленні залежності між вхідними та вихідними сигналами, представленими у часовій області. Для цього звичайно треба знати відповідні характеристики системи, які теж повинні бути залежними від дискретного часу. Тому в цьому підрозділі спочатку зупинимось на визначенні таких часових характеристик. При цьому, для спрощення записів, будемо розглядати дискретні сигнали, аргументом яких є нормований час.

Суть таких часових характеристик ЛДС полягає в наступному. Дискретні сигнали, що використовуються в системах ЦОС, досить різноманітні. І щоб уніфікувати задачу аналізу їх проходження через ЛДС треба мати можливість представляти такі складні сигналі у вигляді зваженої суми деяких стандартних сигналів. Тоді, оскільки ЛДС задовольняють принципу суперпозиції, то можна найти відгук на кожну складову зваженої суми, результат скласти і знайти відгук на весь складний сигнал. Тим самим отримати відповідь на задачу аналізу проходження складного сигналу через ЛДС. Отже треба знати реакцію ЛДС на дію стандартного сигналу. Таким чином, часові характеристики ЛДС представляють собою реакції на певні стандартні дискретні сигнали.

В теорії ЛДС такими стандартними сигналами є одиничний імпульс і функція у вигляді одиничного стрибка. Розглянемо перший стандартний сигнал – одиничний імпульс. Будемо визначати його наступним виразом:

(3.7)

На рис. 3.2 зображено одиничний імпульс.

Рис. 3.2. Одиничний імпульс

Можна розглядати також зсунуті у часі одиничні імпульси. Затриманий у часі на дискретних інтервалів одиничний імпульс (див. рис. 3.3, а) запишеться так:

(3.7А)

а б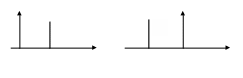

Рис. 3.3. Затриманий у часі а) і випереджаючий б) одиничні

імпульси

Випереджаючий на дискретних інтервалів одиничний імпульс (рис. 3.3, б)

(3.7Б)

В усіх трьох виразах (3.7), (3.7А) і (3.7Б) дискретна змінна

Розглянемо тепер деяку нестаціонарну ЛДС, яка носить назву параметричної. Будемо вважати, що математична модель такої системи описується лінійним оператором , який залежить не лише від вхідної дії , а і від нормованого дискретного часу . Нехай система знаходиться в нульовому стані, тобто до моменту всі вхідні сигнали тотожно дорівнюють нулеві і маємо нульові початкові умови, а саме при відгук теж дорівнює нулеві: . Якщо на таку систему подати на вхід у момент часу тестовий одиничний сигнал (3.7), то на виході отримаємо відгук (рис. 3.4, а)

, (3.8)

де перший аргумент означає поточний нормований дискретний час, а другий аргумент позначає момент подачі тестуючого імпульсу на вхід системи, який у нашому випадку дорівнює нулеві.

Подамо в тих же умовах на вхід параметричної системи зсунутий у часі тестовий сигнал, наприклад, (3.7А). Оскільки для параметричної системи її параметри з часом змінюються, то в цьому випадку відгук буде відрізнятися від відгуку (3.8) (рис. 3.4, б), що відображається тим, що другий аргумент дорівнює , тобто маємо

(3.9)

Таким чином отримуємо наступне означення: відгук параметричної дискретної системи (3.9), яка знаходиться в нульовому стані, на дію тестуючого одиничного сигналу (3.7А), де називається імпульсною характеристикою.

Оскільки для реально існуючих систем повинен виконуватися принцип причинності, а саме, при відсутності на вході впливу на виході відгук теж буде тотожно дорівнювати нулеві, то на імпульсну

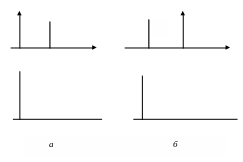
Рис. 3.4. Реакція дискретної параметричної системи на тестуючий імпульс, поданий на вхід у різні моменти часу

характеристику (3.9) накладається обмеження фізичної можливості, тобто для фізично існуючих систем

.

Розглянемо тепер стаціонарну ЛДС. Для такої системи відгук є інваріантним до зсувів вхідного сигналу у часі, тобто оператор , що описує математичну модель системи, тепер не залежить від часового параметра. Нехай система знаходиться в нульовому стані. В момент часу подамо тестовий сигнал (3.7). Тоді відгук (див. рис 3.5, а) запишеться так

. (3.10)

Якщо на лінійну стаціонарну систему, що знаходиться в нульовому стані, подати тестуючий сигнал у момент часу , то відгук

,

тобто буде мати ту ж форму, що і (3.10), але буде зсунутий у часі на інтервалів (рис. 3.5, б).

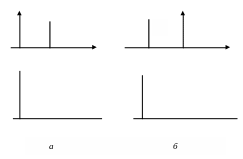
Рис. 3.5. Реакція стаціонарної ЛДС тестуючий імпульс, поданий на вхід у різні моменти часу

Таким чином для стаціонарної ДЛС не важливо, в який момент часу подавати тестуючий сигнал. Форма реакції від цього не залежить (див. рис. 3.5). Тому маємо таке означення: відгук стаціонарної ЛДС (3.10), яка знаходиться в нульовому стані, на дію тестуючого одиничного сигналу (3.7) називається імпульсною характеристикою.

Умова фізичної можливості для фізично існуючих стаціонарних ЛДС в термінах імпульсної характеристики має такий вигляд:

.

Розглянемо тепер другий стандартний сигнал – дискретний одиничний стрибок. Будемо визначати його наступним виразом:

(3.11)

На рис. 3.6 зображено тестовий сигнал у вигляді дискретного одиничного стрибка.

Рис. 3.6. Одиничний стрибок

Можна розглядати також зсунуті у часі одиничні стрибки. Затриманий у часі на дискретних інтервалів одиничний стрибок (див. рис. 3.7, а) запишеться так:

(3.11А)

а б

Рис. 3.7. Затриманий у часі а) і випереджаючий б) одиничні

стрибки

Випереджаючий на дискретних інтервалів одиничний стрибок (рис. 3.7, б)

(3.11Б)

В усіх трьох виразах (3.11), (3.11А) і (311Б) дискретна змінна

Між першим і другим типом тестуючи сигналів існує зв’язок, що виражається наступними співвідношеннями:

(3.12)

і

, (3.13)

де різниця назад

,

а - приріст у дискретному нормованому часі. Тому ми можемо переписати (3.13) так:

(3.13А)

На основі тестуючого сигналу (3.11) можна записати визначення ще однієї часової характеристики лінійних дискретних систем, яка носить назву перехідної характеристики. Оскільки при виведенні означення перехідної характеристики розмірковування будуть подібні до розмірковувань при виведенні означення імпульсної характеристики, то ми зупинимось лише на формулюванні кінцевих означень.

Спочатку розглянемо нестаціонарну дискретну лінійну систему. Реакція параметричної системи, що знаходиться в нульовому стані, на дію одиничного стрибка (3.11) називається її перехідною характеристикою, тобто

, (3.14)

де - поточний дискретний нормований час, а - момент подачі одиничного стрибка.

Таким чином, як і імпульсна характеристика , перехідна характеристика параметричної дискретної системи залежить від двох часових параметрів. На перехідну характеристику (3.14) реально існуючих параметричних систем накладається обмеження фізичної можливості, тобто

.

Перейдемо тепер до стаціонарної ЛДС, математична модель якої описується оператором . Реакція стаціонарної ЛДС, що знаходиться в нульовому стані, на дію одиничного стрибка (3.11) називається її перехідною характеристикою, тобто

(3.15)

Умова фізичної можливості для фізично існуючих стаціонарних ЛДС в термінах перехідної характеристики (3.15) має такий вигляд:

.

Згідно зі співвідношеннями (3.12) і (3.13А) можна записати аналогічного типу співвідношення і між перехідною та імпульсною характеристикою ЛДС. Так імпульсна характеристика

(3.16)

для параметричної дискретної системи і

(3.16А)

для стаціонарної ЛДС. В (3.16) - приріст назад за дискретною змінною .

Перехідна характеристика (3.14) при будь-якому фіксованому

(3.16Б)

для параметричної дискретної системи і

(3.16В)

для стаціонарної ЛДС.

Розглянемо тепер деякий дискретний сигнал

. (3.17)

Такий сигнал можна записати в термінах розглянутих вище стандартних сигналів: одиничного імпульсу (3.7) або одиничного стрибка (3.11). Так на основі одиничного імпульсу запишемо

, (3.18)

тобто сигнал представлений у вигляді зваженої суми зсунутих у часі одиничних імпульсів, роль вагових коефіцієнтів відіграють відповідні відліки сигналу (3.17). Співвідношення (3.18) представляє дискретну згортку самого сигналу (3.17) і одиничного імпульсу (3.7).

Приклад 3.1. Записати значення дискретного сигналу , відліки якого подані в табл. 3.1, у вигляді дискретної згортки (3.18).

Таблиця 3.1

	0	1	2	3	4
	-5	0,5	5	8	4

Використовуючи формулу (3.18) і враховуючи властивості одиничного імпульсу, маємо

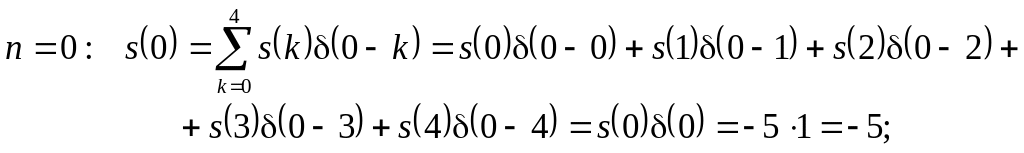
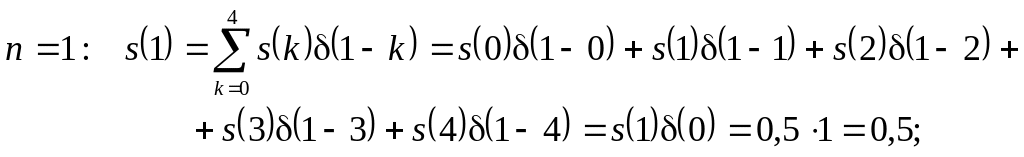
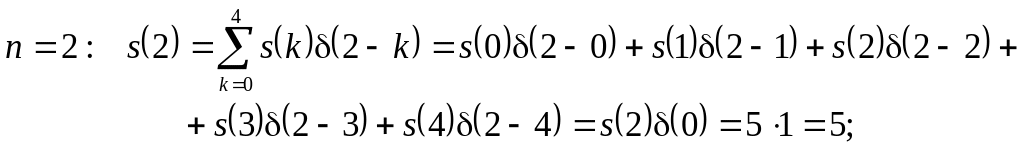
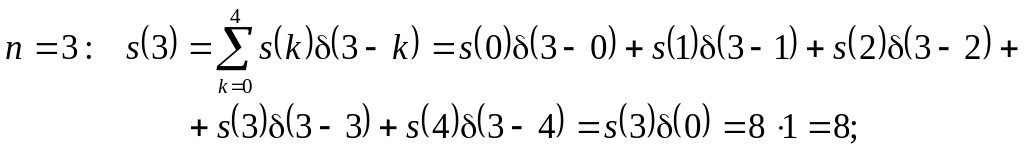
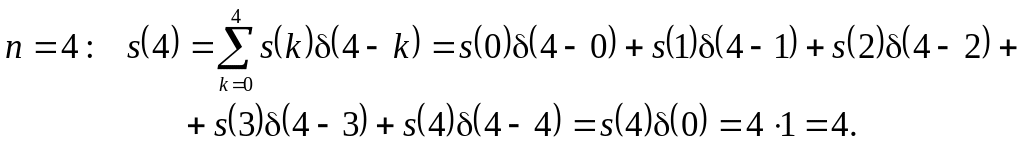На основі одиничного стрибка (3.11) дискретний сигнал (3.17) можна подати у такому вигляді:

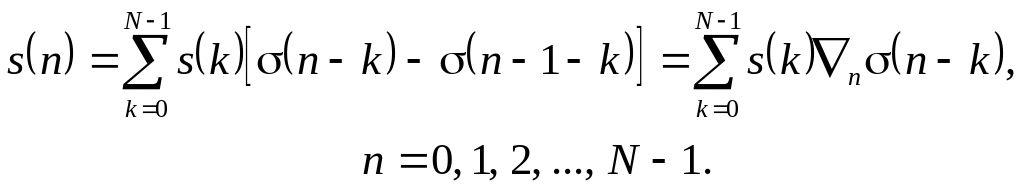(3.19)

Зображення дискретного сигналу на основі одиничного стрибка можна подати і в такому вигляді:

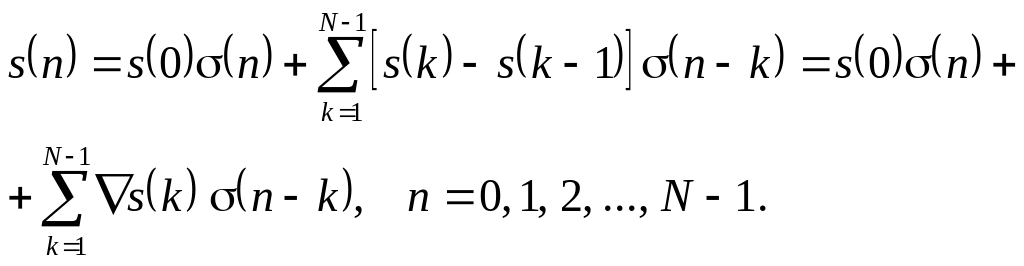(3.19А)

Співвідношення (3.19) і (3.19А) рівноцінні, відрізняються вони лише тим, що в першому випадку береться різниця одиничного стрибка , а в другому випадку – приріст сигналу .

Враховуючи в правій частині співвідношення (3.19) вираз (3.13), бачимо, що, по суті, представлення дискретного сигналу в термінах одиничного стрибка (3.19) співпадає з представленням в термінах одиничного імпульсу (3.18).

Розглянемо тепер параметричну дискретну систему, математична модель якої описується оператором . Нехай система знаходиться в нульовому стані. На вхід такої системи (див. рис. 3. 8) подамо дискретний сигнал (3.17). Потрібно знайти відгук

Рис. 3.1. Дискретна параметрична система

такої системи.

Використовуючи поняття лінійного оператора, запишемо для довільного

.

Підставимо в праву частину останнього співвідношення зображення дискретного сигналу на основі одиничного імпульсу (3.18). Маємо

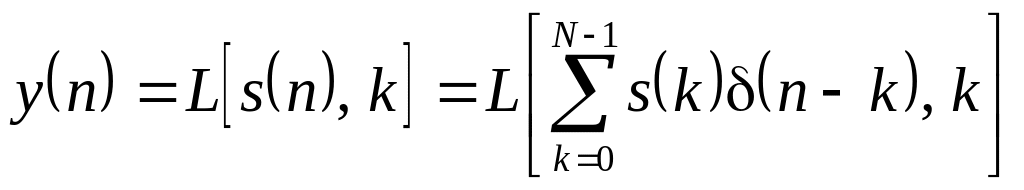. (3.20)

Оскільки оператор задовольняє принципу суперпозиції, то можемо (3.20) переписати так:

.

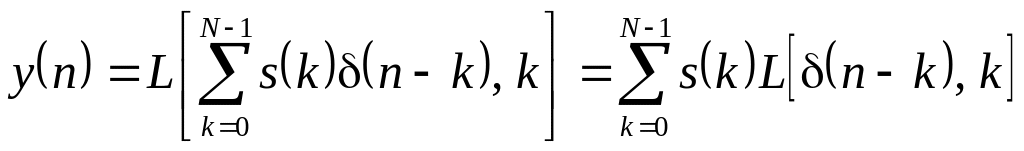Враховуючи означення імпульсної характеристики параметричної системи (3.9), останній вираз можна переписати у такому вигляді:

. (3.21)

Таким чином, якщо на параметричну систему, що знаходиться в нульовому стані, подати дискретний сигнал , то її відгук представляє собою суму добутків відліків вхідного сигналу і імпульсної характеристики, При цьому поточний час імпульсної характеристики співпадає з поточним часом відгуку, а час , що відповідає моменту подачі тестую чого імпульсу, співпадає з моментом , в якому береться відлік вхідного сигналу. Зміст такого представлення вихідного сигналу параметричної системи на дію дискретного сигналу полягає в наступному. Використовуючи представлення вхідного сигналу у вигляді суми окремих складових (3.18), по суті ми «пропускаємо» через параметричну систему кожну елементарну складову і отримані на виході, теж елементарні відгуки , складаємо. Оскільки параметрична система задовольняє принципу суперпозиції, то отримана сума співпадає з відгуком системи на дію вхідного сигналу в цілому.

Розглянемо тепер в тій же постановці аналогічно задачу, але скористаємось представленням вхідного сигналу у термінах одиничного стрибка (3.19). Маємо

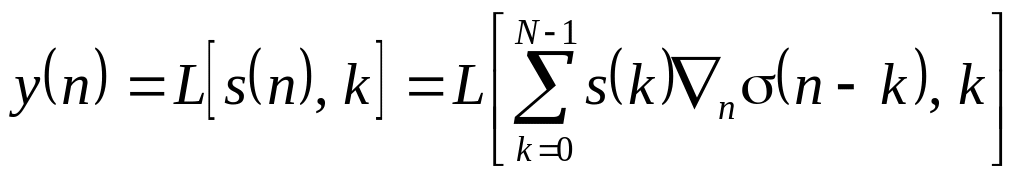
і, враховуючи принцип суперпозиції, далі запишемо

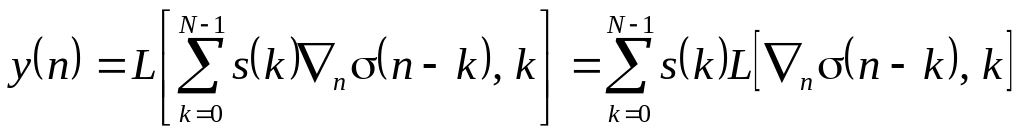. (3.22)

Поміняємо місцями в правій частині співвідношення (3.22) різницевий оператор і оператор системи . Це можливо, оскільки вони обидва є лінійними. Тоді отримаємо

.

Враховуючи означення перехідної характеристика параметричної системи (3.14), остаточно запишемо

. (3.23)

Отже, використовуючи поняття перехідної характеристики дискретної параметричної системи (3.14), її відгук , при кожному фіксованому , на дію дискретного сигналу запишеться у вигляді суми добутків відліків вхідного сигналу і приростів назад перехідної характеристики відносно змінної .

Зазначимо, що співвідношення для знаходження відгуку дискретної параметричної системи на основі її імпульсної характеристики (3.21) і на основі перехідної характеристики (3.23) є рівноцінними. Тим більше, що на основі взаємозв’язків між імпульсною та перехідною характеристиками (див. формули (3.16) і (3.16Б)) можна перейти від одного співвідношення (3.23) до іншого (3.21). Яку формулу все ж використовувати, залежить від конкретного типу задачі, виду вхідного сигналу та параметричної системи. Хоча слід зауважити, що на практиці все ж частіше використовується формула (3.21), оскільки вона простіша.

Розглянемо тепер стаціонарну ЛДС, математична модель якої описується лінійним оператором . Нехай система знаходиться в нульовому стані. На вхід такої системи (див. рис. 3. 9) подамо дискретний сигнал (3.17). Потрібно знайти відгук такої системи.

Розмірковування при виведенні формул для знаходження відгуку стаціонарної ЛДС на основі її часових характеристик аналогічні до розмірковувань при виведенні подібних формул для параметричної системи, що було детально розглянути вище. Тому далі ми не будемо висвітлювати в повному обсязі всі етапи доведення відповідних співвідношень, а запишемо лише остаточні результати. Виведення ж формул залишаємо читачеві.

Рис. 3.9. Стаціонарна ЛДС

На основі означення імпульсної характеристики стаціонарної ЛДС (3.10) та представлення (3.18) скінченого дискретного сигналу (3.17) в термінах одиничного імпульсу відгук запишеться так:

. (3.24)

Таким чином, відгук стаціонарної ЛДС представляє собою дискретну згортку сигналу , що діє на систему, і імпульсної характеристики . Алгоритм (3.24) реалізується наступним чином. При кожному фіксованому , не залежно від його значення, перший співмножник, тобто сигнал залишається «незміщеним» відносно початку координат (точка ), а імпульсна характеристика «розвертається» в дзеркальному порядку відносно вісі ординат і зсувається на дискретних інтервалів вправо відносно початку координат (див. рис. 3.10). Після цього співпадаючі у часі відліки вхідного сигналу і імпульсної характеристики перемножуються і складаються.

Рис. 3.10. Приклад зображення вхідного сигналу та імпульсної характеристики стаціонарної ЛДС відносно початку

координат при фіксованому значенні

Оскільки операція згортки є комутативною, то співвідношення (3.24) можна записати і в іншому вигляді, тобто, коли «незміщеною» залишається імпульсна характеристика, а відносно неї «ковзає» вхідний сигнал. Формула згортки запишеться тоді у такому вигляді:

. (3.24А)

Обидві формули є рівноцінними і яку використовувати, залежить від конкретного виду вхідного сигналу та імпульсної характеристики, а також від думки самого дослідника.

Звернемось тепер до означення перехідної характеристики (3.15) стаціонарної ЛДС. Використовуючи тепер представлення вхідного сигналу на основі одиничного стрибка (3.19), отримаємо такий вираз для відгуку:

. (3.25)

Отже, відгук стаціонарної ЛДС (при застосуванні перехідної характеристики) дорівнює згортці вхідного сигналу та різниці назад

перехідної характеристики.

Приклад 3.2. Стаціонарна ЛДС має імпульсну характеристику, подану в табл. 3.2. На вході такої системи діє сигнал, заданий в

Таблиця 3.2

	0	1	2	3	4
	2	1,5	1,0	0,5	0

табл. 3.1 (приклад 3.1). Потрібно знайти відгук на виході.

Використовуючи формулу (3.24), при знаходимо

При

При

Зауважимо, що при розрахунках враховується умова фізичного існування системи, тобто при від’ємних значеннях . Подальші розрахунки виконуються аналогічно, тому ми не будемо їх розписувати детально, а розглянемо ще випадок, коли

В останньому співвідношенні враховується, що імпульсна характеристика системи обмежена, тобто після відліку з всі наступні значення імпульсної характеристики дорівнюють нулеві. З цієї причини і всі подальші значення відгуку теж будуть дорівнювати теж нулеві.

Результати розрахунків відгуку стаціонарної ЛДС зведемо до табл. 3.3.

Таблиця 3.3

	0	1	2	3	4	5	6	7	8
	-10	-6,5	5,75	21,5	25,75	16,5	8,0	2,0	0

На рис. 3.11 зображені вхідний сигнал, імпульсна характеристика і відгук.

Рис. 3.11. Зображення вхідного сигналу (а), імпульсної характеристики (б) та відгуку (в) стаціонарної ЛДС

Приклад 3.3. Виконати розрахунки відгуку стаціонарної ЛДС в умовах прикладу 3.2, використовуючи перехідну характеристику.

Перш за все на основі співвідношення між перехідною та імпульсною характеристиками (3.16В) знайдемо, маючи відліки імпульсної характеристики, відліки перехідної характеристики. Згідно з даними табл. 3.2 та виразу (3.16В), а також враховуючи умови фізичної можливості, для нашого випадку маємо

Значення перехідної характеристики при

Значення перехідної характеристики при

Значення перехідної характеристики при

Значення перехідної характеристики при

Значення перехідної характеристики при

Всі подальші значення перехідної характеристики дорівнюють одному і тому ж числу, тобто при . Вид перехідної характеристики зображений на рис. 3.12.

Рис. 3.12. Зображення перехідної характеристики

стаціонарної ЛДС

Розрахуємо тепер відгук системи. Застосуємо для цього формулу (3.25), яка для нашого прикладу має вигляд

.

При

При

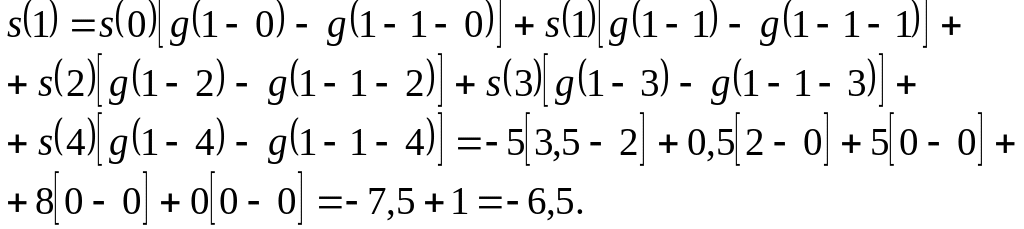
При

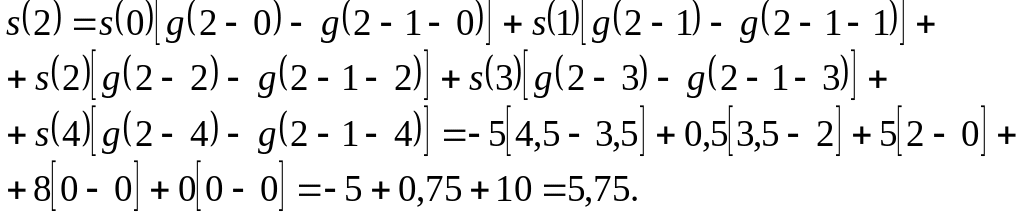
Для подальших розрахунків запишемо остаточні результати: при ; при ; при ; при ; при ; при . І далі при всіх .

Отже бачимо, що результати розрахунків відгуку стаціонарної ЛДС при застосуванні як імпульсної характеристики, так і перехідної співпадають.

І все ж на практиці частіше застосовується для опису ЛДС у часі імпульсна характеристика. Обумовлено це більшою простотою алгоритмів обчислення відгуків ЛДС на основі імпульсної характеристики (див. формулу (3.21) – для параметричних дискретних систем і формулу (3.24) – для стаціонарних ЛДС). Так, аналогічного типу співвідношення на основі перехідної характеристики вимагають додаткового застосування різницевого оператора (формула (3.23) – для параметричних дискретних систем і формула (3.25) – для стаціонарних ЛДС). Тому при подальшому описові ЛДС ми в основному будемо розглядати в якості їх часової характеристики імпульсну характеристику.

Ми розглянули зображення ЛДС у часовій області на основі їх часових же характеристик: імпульсної і перехідної. Існує ще один спосіб опису ЛДС у часі. Для аналогових лінійних систем подібний опис здійснюється на основі диференційних рівнянь з постійними коефіцієнтами (стаціонарні лінійні системи) або з коефіцієнтами, що залежать від часу (параметричні системи). Аналогом такого опису для ЛДС є застосування різницевих рівнянь. Таке рівняння у загальному виді ми вже розглядали в підрозділі 3.1., формула (3.6). Перепишемо це рівняння для нормованого часу, врахувавши при цьому, що приріст нормованої дискретної часової змінної . Тому маємо

(3.26)

де всі коефіцієнти і - є постійними числами для стаціонарних ЛДС. В разі, коли хоча б один із вказаних коефіцієнтів залежить від часу, то ми маємо справу з параметричною дискретною системою.

Враховуючи в рівнянні (3.26) загальний вираз (3.6А) для приросту -го порядку

, ,

де

,

і поєднавши після цього подібні доданки, отримаємо

(3.27)

де і - числові коефіцієнти, які представляють певні суми із коефіцієнтів і відповідно при поєднанні подібних доданків.

Розв’язавши рівняння (3.27) відносно відгуку ЛДС системи, знаходимо

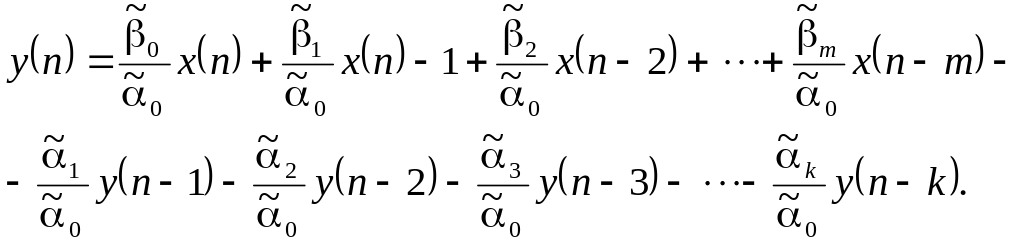(3.28)

Введемо позначення

та

і перепишемо (3.28) так

. (3.29)

Співвідношення (3.29) представляє собою алгоритм обробки ЛДС вхідного дискретного сигналу , на виході якої отримуємо відгук . Як видно із формули (3.29), відгук ЛДС у момент часу дорівнює сумі значення вхідного сигналу у той же момент часу і декількох попередніх значень вхідного сигналу та вихідного з відповідними ваговими коефіцієнтами. Отже, алгоритм (3.29) зводиться до наступних операцій:

1. Запам’ятовування попередніх відліків вхідного сигналу.

2. Запам’ятовування попередніх відліків вихідного сигналу.

3. Множення запам’ятованих вхідних і вихідних відліків на відповідні коефіцієнти.

4. Складання, отриманих після множення, добутків з вхідним відліком .

Числа і визначають порядок ЛДС, тобто, якщо позначити порядок системи літерою , то

.

Розглянемо два лінійних оператори і . Перший діє на вхідний сигнал і, згідно з (3.29), визначається наступним виразом:

. (3.30)

Другий оператор діє на вихідний сигнал і, згідно з (3.29), визначається так:

. (3.31)

На основі введених позначень (3.30) і (3.31), алгоритм (3.29) можна записати у такому вигляді:

.

Тоді, відповідно до цього запису, умовне зображення ЛДС (див. рис. 3.8 або рис. 3.9) може бути представлено у вигляді двох блоків (рис. 3.13). На цій схемі перший блок з оператором будемо називати прямим блоком, розуміючи під цією назвою те, що в цьому блоці ведеться обробка вхідного сигналу і який проходить зліва направо, з входу на вихід. У прямому блоці, згідно з (3.30), відбуваються послідовні зсуви на один інтервал дискретизації відліків вхідного сигналу та множення їх на відповідні коефіцієнти .

Другий блок з оператором будемо називати оберненим блоком, розуміючи під цією назвою те, що в цьому блоці ведеться обробка вихідного сигналу і який проходить з права наліво, з виходу до входу. Тобто, іншими словами, цей блок утворює зворотний зв’язок, передає сигнал у зворотному напрямку по відношенню до першого блоку. У зворотному блоці, згідно з (3.31), відбуваються послідовні зсуви на один інтервал дискретизації відліків вихідного сигналу та множення їх на відповідні коефіцієнти .

Третій блок, зображений на рис. 3.13, позначений знаком «+», будемо називати блоком-суматором. У цьому блоці сигнали, вироблені прямим блоком і оберненим блоком, підсумовуються, згідно з формулою (3.29). Ця сума і представляє значення відгуку . При цьому в блоці-суматорі виконується алгебраїчне підсумовування, тобто в залежності від знаку вагових коефіцієнтів і в (3.29), це може бути і додавання і віднімання сигналів.

Як видно із рис. 3.13, сигнали в прямому блоці проходять з входу на вихід через суматор в одному напрямі. В зворотному ж блоці сигнали через суматор циркулюють по замкненому колу. Але саме така нескінченна циркуляція відліків вихідного сигналу призводить до того, що для таких систем виникають проблеми стійкості, про що буде йти мова дещо далі.

Рис. 3.13. Структурна схема рекурсивної ЛДС

ЛДС, алгоритм роботи яких описується співвідношенням (3.29), називаються рекурсивними. У таких систем хоча б один коефіцієнт оператора (3.31) не дорівнює нулеві. Іншими словами, для рекурсивних систем визначальним є наявність зворотного зв’язку.

Якщо в співвідношенні (3.29) всі коефіцієнти , то для формування відгуку в момент часу враховуються значення вхідного сигналу у той же момент часу і декілька попередніх значень лише вхідного сигналу . В таких ЛДС зворотний зв’язок відсутній. Такі системи називаються не рекурсивними. Їх алгоритм роботи описується співвідношенням

, (3.29А)

а структурна схема зображена на рис. 3.14.

Рис. 3.14. Структурна схема нерекурсивної ЛДС

Приклад 3.4. Стаціонарна ЛДС описується різницевим рівнянням 2-го порядку

. (3.32)

Побудувати алгоритм обробки дискретних сигналів цією системою і визначити оператори прямого та оберненого блоків.

На основі означення оператора приросту назад -го порядку (3.6А), запишемо

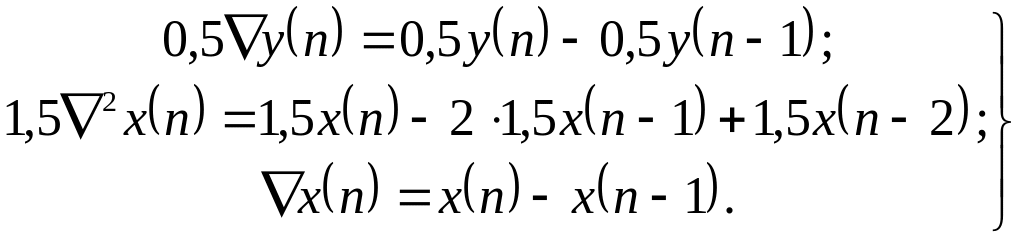(3.33)

Підставимо вирази (3.33) в (3.32) і отримаємо

або, об’єднавши подібні члени, запишемо різницеве рівняння у такому вигляді:

Запишемо останнє рівняння відносно відліку вихідного сигналу

(3.34)

Це і буде шуканий алгоритм перетворення (обробки) заданою в прикладі ЛДС вхідного сигналу в вихідну реакцію .

Порівнюючи загальний вираз для алгоритму роботи рекурсивної ЛДС (3.29) і отриманий алгоритм (3.34), можемо зробити висновок, що оператор прямого перетворення

,

тобто, згідно з (3.30) і ,

а оператор зворотного зв’язку

,

тобто згідно з (3.31) і .

Знайдемо імпульсну характеристику рекурсивної стаціонарної ЛДС, використовуючи загальний вираз для алгоритму її роботи (3.29). Для цього, згідно з означенням імпульсної характеристики, при нульових початкових умовах подамо у момент часу тестуючий сигнал (3.7) (див. рис. 3.2) і будемо на основі алгоритму (3.29) знаходити значення відгуку , який в даному випадку і буде представляти відліки імпульсної характеристики

Для моменту часу маємо

Для , тобто через відрізок часу, рівний інтервалу дискретизації,

Ще через відрізок часу, рівний інтервалу дискретизації, тобто при

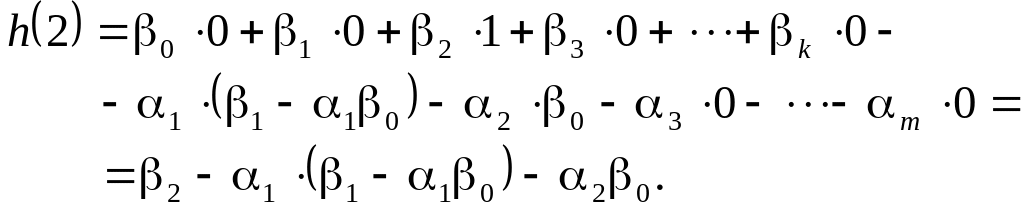
На наступному кроці, при

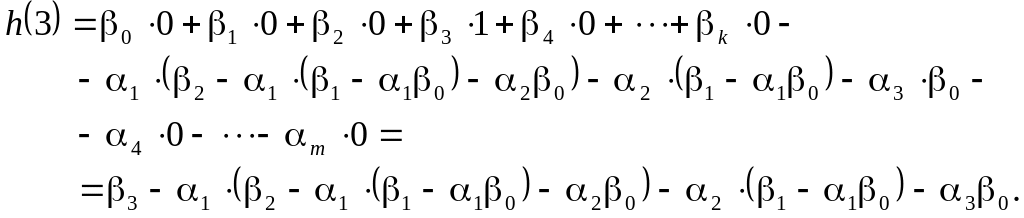
Подібний процес формування відліків імпульсної характеристики буду продовжуватися до моменту часу , тобто поки одиничний тестовий сигнал не «пройде» всі зміщень в блоці прямого перетворення з оператором . Після цього при всіх наступних значеннях оператор буде «видавати» на виході значення, рівні нулеві. І все ж ненульові відліки імпульсної характеристики будуть продовжувати формуватися і при внаслідок наявності блоку зворотного зв’язку. Іншими словами, сигнал буде продовжувати «циркулювати» між виходом системи і блоком зворотного зв’язку з оператором . При цьому цей процес «циркулювання», у всякому разі теоретично, буде продовжуватися до нескінченності. Значення ж вихідного сигналу, тобто значення імпульсної характеристики, будуть асимптотично спадати до нуля (монотонно, або у вигляді коливального процесу), або деяким чином зростати (до нескінченності, або прямувати до деякої константи) в залежності від значень коефіцієнтів оператора зворотного зв’язку. Деякі можливі варіанти імпульсних характеристик рекурсивних ЛДС показані на рис. 3.15.

Отже в рекурсивної ЛДС імпульсна характеристика нескінчення (за кількістю відліків у часі), тому часто їх називають ЛДС з нескінченною імпульсною характеристикою, або, скорочено, НІХ-системи.

Наведені вище розрахунки значень імпульсної характеристики (для перших чотирьох значень , тобто ) показують, що для рекурсивної ЛДС (НІХ-системи) відліки імпульсної характеристики залежать у загальному випадку нелінійно від коефіцієнтів , що входять до виразу (3.30) оператора прямого перетворення , і коефіцієнтів , що входять до виразу (3.31) оператора зворотного перетворення .

Рис. 3.15. Імпульсні характеристики рекурсивних ЛДС

Приклад 3.5. Для рекурсивної ЛДС (означеної в прикладі 3.4 різницевим рівнянням (3.32)) знайти імпульсну характеристику.

Для знаходження імпульсної характеристики використаємо отриманий у прикладі 3.4 алгоритм (3.34). Для цього, згідно з означенням імпульсної характеристики, підставимо при нульових початкових умовах в (3.34) в якості вхідного сигналу одиничний тестуючий сигнал (3.7).

Розглянемо момент часу

В наступний момент часу тестуючий сигнал буде зсунутий у часі на один крок дискретизації, тобто будемо мати сигнал , і тоді

Ще через один крок дискретизації будемо мати сигнал і значення імпульсної характеристики

Далі, розмірковуючи аналогічно, отримаємо при і відповідно

І так далі аналогічно. Отже, починаючи з моменту часу імпульсна характеристика

Таким чином ми маємо у цьому випадку НІХ-систему, у якої імпульсна характеристика з ростом прямує до нуля, тобто

.

Для ілюстрації на рис. 3.16, за результатами розрахунків, наведено графік імпульсної характеристики розглянутої в прикладі ЛДС.

Рис. 3.16. Імпульсні характеристики рекурсивних ЛДС з різницевим рівнянням (3.32)

Розглянемо нерекурсивну стаціонарну ЛДС, алгоритм роботи якої описується співвідношенням (3.29А). На основі цього алгоритму розрахуємо імпульсну характеристику. При маємо

.

При .

При .

……………………………………………………………………

При .

Далі, при всіх значеннях дискретного часу , значення імпульсної характеристики . Таким чином, тепер маємо скінчену (у часі, за кількістю відліків) імпульсну характеристику. Кількість відліків імпульсної характеристики дорівнює кількості коефіцієнтів в різницевому рівнянні (3.29А), що описує алгоритм роботи нерекурсивної ЛДС. Значення ж відліків імпульсної характеристики співпадають зі значеннями відповідних (за номером) коефіцієнтів . Такі ЛДС отримали назву систем зі скінченою імпульсною характеристикою, або скорочено СІХ-системи.

Приклад 3.6. Розглянемо стаціонарну ЛДС, розглянуту в прикладі 3.4, в якій відсутній зворотній зв’язок, тобто будемо вважати, що в алгоритмі (3.34) коефіцієнт при дорівнює нулеві. У цьому випадку отримуємо нерекурсивну ЛДС з алгоритмом роботи

. (3.35)

Знайдемо її імпульсну характеристику, поклавши в (3.35) вхідний сигнал . Маємо

Далі, при всіх подальших значеннях , імпульсна характеристика .

Отже тепер імпульсна характеристика (рис. 3.17) скінчена (у часі) і ми маємо СІХ-систему. Імпульсна характеристика біполярна,

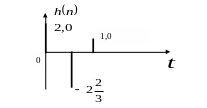
Рис. 3.17. Імпульсні характеристики СІХ-системи

тобто маємо і додатні, і від’ємні значення.

Розглянемо питання, пов’язане з особливостями формування вихідного сигналу ЛДС. Згідно з розглянутими вище загальними алгоритмами роботи ЛДС у часі (3.21), (3.23), (3.24), (3.25), (3.29) і (3.29А) при формуванні вихідного відліку у момент часу враховуються не лише значення вхідного сигналу у той же момент часу , а і ряд попередніх значень того ж таки вхідного сигналу , тобто враховується «передісторія» вхідного сигналу ЛДС. Іншими словами, система «пам’ятає» про те, що відбувалося з вхідним сигналом до моменту часу . У цьому полягає властивість інерційності ЛДС, тобто припинення подачі сигналу на її вході ще не означає, що система не буде певний час виробляти ненульові значення вихідного сигналу. Тривалість такого процесу, тобто кількість вироблених відліків вихідного сигналу після припинення дії вхідного сигналу залежить від тривалості «пам’яті» системи.

Тривалість «пам’яті» залежить від виду імпульсної характеристики системи, а саме, від кількості ненульових її відліків. Згідно з алгоритмом (згортка (3.24)), нульове значення імпульсної характеристики враховує, при формуванні відліку у момент часу , значення вхідного сигналу теж у момент часу . Всі наступні значення імпульсної характеристики, тобто при враховують минуле, тобто попередні значення сигналу , де . Для цього імпульсна характеристика і «розвертається» в дзеркальному порядку відносно початку координат (див. рис. 3.10).

Оскільки, як ми з’ясували вище, імпульсна характеристика не рекурсивних ЛДС скінчена, то і при формуванні відгуку враховується лише скінчена кількість попередніх значень вхідного сигналу. Отже тривалість «пам’яті» таких систем скінчена. Для не рекурсивних ЛДС, згідно з формулою (3.29А), враховується попередніх відліків вхідного сигналу. І чим більше значення , тим більша тривалість пам’яті нерекурсивної ЛДС. Але оскільки число скінчене, то і «пам’ять» обмежена. Таким чином, якщо для не рекурсивної ЛДС припинити подачу на її вхід сигналу у деякий момент часу , то система буде видавати ненульові значення відгуку у наступні моменти часу , де . Після моменту всі значення відгуку будуть дорівнювати нулеві, тобто

.

Для рекурсивної ЛДС імпульсна характеристика нескінченна (див. рис. 3.16 і приклад 3.5) і тому при формуванні вихідного відліку сигналу у момент часу враховується вся «передісторія» процесів у системі до цього моменту часу, аж до мінус нескінченності (у всякому разі теоретично). Отже, якщо у момент часу припинити подачу на вхід рекурсивної системи вхідного сигналу , вона все одно буде продовжувати (як би за «інерцією») виробляти ненульові значення вихідного сигналу до нескінченності (в усякому разі теоретично). При цьому значення будуть зменшуватися³, поступово прямуючи до нуля, тобто

.

Швидкість спадання значень відгуку залежить (прямо пропорційно) від швидкості спадання значень імпульсної характеристики (див. рис. 3.16 та результати розрахунку в прикладі 3.5).

Тому кажуть, що рекурсивні ЛДС мають нескінченну «пам’ять». Це є наслідком того, що в цих системах існує зворотній зв’язок. Тому, хоча дія вхідного сигналу і припиняється, ланцюг зворотного зв’язку (див. рис. 3.13) не розривається і відліки сигналу з виходу продовжують подаватися на вхід системи. І, таким чином, відліки сигналу продовжують «циркулювати» у рекурсивній ЛДС, як би по колу, до нескінченності, поступово затухаючи (див. зноску 3).

Повернемось знову до прикладу 3.5. Згідно з умовою задачі, ми отримали спадну у часі імпульсну характеристику. Це є наслідком того, що коефіцієнт , а саме . Як би ми мали випадок, що , то імпульсна характеристика була б після моменту часу постійною у часі, тобто

.

У тому ж випадку, коли , імпульсна характеристика після моменту часу буде монотонно зростати.

Отже у цьому прикладі ми маємо три варіанти поведінки ЛДС у часі. У першому випадку, коли імпульсна характеристика затухає, тобто

,

маємо стійку систему. У третьому випадку, коли імпульсна характеристика з ростом зростає, маємо нестійку систему. Другий із розглянутих варіантів, коли імпульсна характеристика прямує до деякого постійного значення, є граничним між першим і другим випадками.

Таким чином, виникає питання стійкості ЛДС, яке полягає в наступному. Справа в тому, що перевірити стійкість ЛДС згідно з формулюваннями попереднього абзацу буває досить складно. Тому потрібно встановити критерії стійкості ЛДС на основі тих чи інших характеристик чи параметрів системи, зокрема на основі часових характеристик. Розглянемо це питання детальніше. Для цього дамо ряд означень відносно поняття стійкості.

ЛДС вважається стійкою, якщо в разі припинення подачі на вхід сигналу (або через певний час після припинення подачі вхідного сигналу) вихідна реакція теж припиняється чи починає спадати (монотонно або коливальним чином), поступово прямуючи до нуля.

Процеси, що відбуваються в ЛДС після припинення подачі вхідного сигналу, зокрема на виході системи, носять назву вільних коливань. Вони обумовлені лише початковими умовами (в момент припинення подачі вхідного сигналу) та властивостями (параметрами) самої системи. Отже якщо вільні коливання в системі затухають, або зовсім припиняються після певної кількості дискретних моментів часу, то система буде стійкою.

Враховуючи співвідношення (3.29), розглянемо неоднорідне різницеве рівняння ЛДС такого виду:

.

Якщо в цьому рівнянні покласти, що сигнал тотожно дорівнює нулеві, то отримаємо однорідне різницеве рівняння

, (3.36)

розв’язок якого при заданих початкових умовах

(3.37)

і буде представляти собою вільні коливання ЛДС. Звичайно, якщо початкові умови є нульовими, тобто

(3.38)

то загальний розв’язок рівняння (3.36) буде нульовим. Це узгоджується із принципом причинності: якщо в даний момент, тобто при , і в минулому на систему не діяли ніякі зовнішні впливи і вона не мала ніяких запасів енергії, то і на виході буде відсутній відгук. Якщо ж в (3.37) хоча б одне значення не дорівнює нулеві, то отримаємо ненульові вільні коливання.

Отже, якщо розв’язок однорідного різницевого рівняння при обмежених початкових умовах (3.37)

(3.39)

при прямує до нуля, то система є стійкою. В (3.39) індекс «В» позначає те, що це є вільні коливання системи, - константи, які визначаються початковими умовами (3.37), - корені характеристичного рівняння

,

що відповідає однорідному різницевому рівнянню (3.36). (Добавити текст про розв’язок загального різницевого рівняння ЛДС на основі характеристичного рівняння, воно подібне до рівняння для полюсів системної функції, і далі перейти до стійкості, Але це мабуть треба описати , де буде опис ЛДС в -області).

Слід зауважити, що для нерекурсивної ЛДС однорідне різницеве рівняння, тобто коли зовнішній вплив , не існує, так само як і його розв’язок. Таким чином, для нерекурсивних ЛДС вільні коливання тотожно дорівнюють нулеві і для них проблема стійкості відсутня. Нерекурсивні ЛДС завжди є стійкими.

Приклад 3.7. Для ЛДС, що описується різницевим рівнянням (3.34) (див приклад 3.4) знайти вільні коливання за початкової умови .

Поклавши в (3.34) вхідний сигнал тотожно рівним нулеві, тобто , отримаємо однорідне різницеве рівняння

(3.40)

для якого характеристичне рівняння має вид:

.

Розв’язком цього рівняння є корінь . Тоді

.

Стала визначається на основі початкової умови , з урахуванням якої утворюємо рівняння

,

звідки .

Отже загальним розв’язком рівняння (3.40) запишеться у такому вигляді:

(3.41)

Зображення коливання (3.41) показано на рис. 3.18. Як видно з

Рис. 3.18. Вільні коливання в ДЛС

рис. 3.18 і, згідно з формулою (3.41), вільні коливання досить швидко затухають, тобто

.

Таким чином, ЛДС, що розглядається в прикладі, є стійкою.

Можна сформулювати поняття стійкості ЛДС і дещо по іншому. Нехай на систему діє обмежений за значеннями вхідний вплив. У цьому випадку вихідна реакція ЛДС є сумою двох складових: вільних і вимушених. Вільні коливання залежать від початкових умов, а вимушені зумовлені дією вхідного впливу. У цьому випадку хоч система і є стійкою, вихідна реакція з ростом не обов’язково прямує до нуля. Важливим є щоб реакція була обмеженою за значеннями. Означення стійкості ЛДС в такій постановці формулюється так.

ЛДС називається стійкою при дії на вході обмеженого за значеннями сигналу , а саме, при всіх

, (3.42)

де - будь-яке, як завгодно велике, але скінчене число, і при обмежених початкових умовах відгук системи теж представляє собою обмежену дискретною функцією часу, тобто при всіх

, (3.43)

де - будь-яке, як завгодно велике, але скінчене число.

Оскільки як вільні коливання, так і відгук ЛДС на зовнішній вплив значною мірою залежать від значень коефіцієнтів і різницевого рівняння (3.29), то від них значною мірою залежить і стійкість системи. (Добавити, при потребі, критерії стійкості на основі значень коефіцієнтів різницевого рівняння, наприклад, критерій Гурвіца та інш.).

Питання стійкості ЛДС можна розглядати і з використанням таких їх часових характеристик, як імпульсна характеристика. Зупинимось на стаціонарних ЛДС. Зрозуміло, що згідно з наведеним вище означенням стійкості системи та враховуючи алгоритм обробки сигналів ЛДС у вигляді різницевого рівняння(3.29), або дискретної згортки (3.24), при обмежених вхідному сигналі і початкових умовах сигнал на виході також буде обмеженим, якщо імпульсна характеристика ЛДС з ростом певною мірою спадає і спадає таким чином, щоб при як завгодно великому суми (3.24) збігалася. Звідси випливає такий критерій стійкості ЛДС: необхідною умовою стійкості ЛДС з імпульсною характеристикою є абсолютна збіжність ряду

. (3.44)

Дійсно, використовуючи формулу⁴ (3.24А), відгук ЛДС можна записати у такому вигляді:

На основі останнього співвідношення для модуля відгуку ЛДС маємо

Далі, згідно з властивостями модуля суми, отримуємо таку нерівність:

. (3.45)

Згадаємо тепер означення стійкості ЛДС. У відповідності з цим означенням вимагається, щоб вхідний вплив системи був обмеженим (див. формулу (3.42)). Враховуючи цей факт в співвідношенні (3.45), ми тільки підсилимо цю нерівність, тобто

(3.46)

Згідно з умовою (3.44) для стійкої системи, сума в правій частині (3.46) є обмеженою. Тоді, позначивши її числом , можемо записати, що і добуток , оскільки співмножники обмежені, теж буде обмеженим, тобто . При цьому остання нерівність виконується при будь-якому і, ввівши позначення , можемо записати

.

Отже, якщо виконується умова (3.44), то, згідно з означенням, система є стійкою. Отже умова (3.44) є необхідною для цього.

Ця умова буде і достатньою для стійкості ЛДС, якщо її доповнити ще такою умовою: в розкладенні⁵ дискретної функції , що є імпульсною характеристикою ЛДС,

ні один із коефіцієнтів розкладення не дорівнює нулеві.

Приклад 3.8. Використовуючи результати розрахунків значень імпульсної характеристики рекурсивної ЛДС (див. приклад 3.5), встановити, чи задовольняє вона необхідній умові стійкості (3.44).

Знайдемо суму модулів значень імпульсної характеристики

.

Отже для даної ЛДС виконується необхідна умова стійкості згідно з (3.44). До з’ясування достатності цієї умови для стійкості ЛДС, що розглядається в даному прикладі, ми повернемось у наступному підрозділі, де буде висвітлено опис систем у комплексній -області.