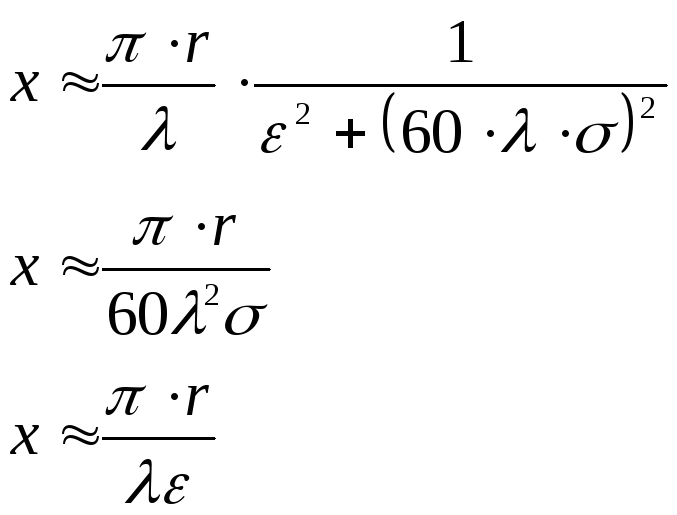- •Глава 1. Уравнения электромагнитного поля
- •Глава 2. Граничные условия
- •Глава 3. Плоские электромагнитные волны и их свойства
- •Глава 4. Линии передачи электромагнитной энергии
- •Глава 5. Основы распространения радиоволн в свободном пространстве
- •Глава 1. Уравнения электромагнитного поля
- •Глава 2. Граничные условия
- •Глава 3. Плоские электромагнитные волны и их свойства
- •Глава 4. Линии передачи электромагнитной энергии
- •Глава 5. Основы распространения радиоволн в свободном пространстве
Глава 5. Основы распространения радиоволн в свободном пространстве
Основные понятия
Радиоволны
– это электромагнитные волны, диапазон
частот которых изменяется в пределах
![]() Гц. Такое
ограничение диапазона сделано условно.
Указанный спектр частот принято
классифицировать по соответствующим
диапазонам (таблица 5.1).
Гц. Такое
ограничение диапазона сделано условно.
Указанный спектр частот принято
классифицировать по соответствующим
диапазонам (таблица 5.1).
Таблица 5.1. Классификация радиоволн по диапазонам.
|
Нижняя граница |
Диапазон |
Верхняя граница | ||
|
f, Гц |
, м |
f, Гц |
, м | |
|
310-3 (3 МГц) |
1011 |
Радиоволны инфразвуковых и звуковых частот |
3103 |
105 |
|
3103 (3 кГц) |
105 |
Сверхдлинные волны (СДВ) |
3104 |
104 |
|
3104 (30 кГц) |
104 |
Длинные волны (ДВ) |
3105 |
103 |
|
3105 (300 кГц) |
103 |
Средние волны (СВ) |
3106 |
102 |
|
3106 (3 МГц) |
102 |
Короткие волны (КВ) |
3107 |
10- |
|
|
|
Ультракороткие волны: |
|
|
|
3107 (30 МГц) |
10 |
метровые (МВ) |
3108 |
1 |
|
3108 (300 МГц) |
1 |
дециметровые (ДМВ) |
3109 |
10-1 |
|
3109 (3 ГГц) |
10-1 |
сантиметровые (СМВ) |
31010 |
10-2 |
|
31010 (30 ГГц) |
10-2 (1 см) |
миллиметровые (ММВ) |
31011 |
10-3 |
|
|
|
Оптические волны: |
|
|
|
31011 (300 ГГц) |
10-3 (1 см) |
инфракрасные (ИКЛ) |
41014 |
7,510-7 |
|
41014 (400 ТГц) |
7,510-7 (0,75 мк = 7500 А) |
видимый свет |
7,51014 |
410-7 |
|
7,51010 (750 ТГц) |
410-7 (0,4 мк = 4000 А) |
ультрафиолетовые (УФЛ) |
31015 (300 ТГц) |
10-7 (0,1 мк = 1000 А) |
Часто удобно выразить частоту радиоволн не в герцах, а в производных единицах измерения. Для этого применяют следующие единицы:
1 мГц (миллигерц)
=
![]() Гц,
Гц,
1 кГц (килогерц) =
![]() Гц,
Гц,
1 МГц (мегагерц) =
![]() Гц,
Гц,
1 ГГц (гигагерц) =
![]() Гц,
Гц,
1 ТГц (терагерц) =
![]() Гц.
Гц.
Предметом нашего изучения являются свободно распространяющиеся радиоволны. Поясним содержание такого термина. Под свободно распространяющимися радиоволнами понимают радиоволны, распространяющиеся в среде без направляющей системы. Волны могут распространяться в атмосфере, толще Земли и океане, но никакой линии передачи в виде жесткой конструкции не применяется.
Свободно распространяющиеся волны применяются для радиосвязи, радиолокационного наблюдения, телеуправления и решения других многочисленных практических задач.
В любом случае используют линию связи, называемую радиолинией. Радиолиния включает три составные части: передатчик, приемник и среду, в которой происходит распространение волны. В радиолиниях со свободно распространяющимися волнами средой является природная среда. Именно в ней происходит распространение электромагнитных волн из пункта передачи (А) в пункт приема (В).
Радиолинии классифицируют по трем типам:
Простейшая радиолиния.
Радиорелейная линия связи.
Вторичная радиолиния.
Рассмотрим сущностные признаки каждой из них.
Простейшая линия содержит передатчик и приемник, расположенные на ее концах (рис.5.1).
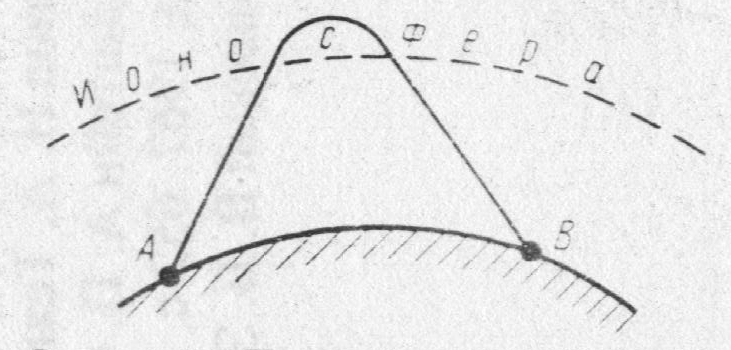
Рис.5.1 Простейшая радиолиния:
А - передатчик, В – приемник.
На рис.5.1 показано, что сигнал выходит из пункта передачи А и приходит в пункт приема В за счет отражения от слоя ионосферы, т. е. схематично показан вид односкачковой трассы.
Далеко не всегда можно обеспечить связь с помощью простейших линий. Часто рельеф местности является сложным, и сигнал в пункт назначения может прийти за счет промежуточных релейных (трансляционных) станций. На рис.5.2 приведена схема такой радиорелейной линии связи.
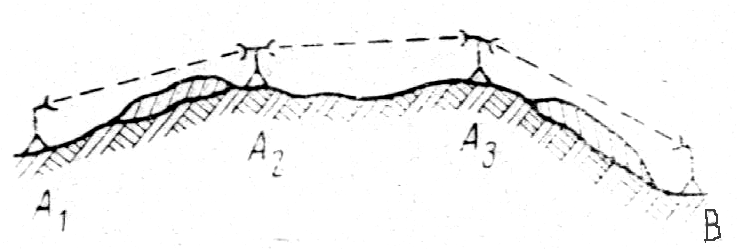
Рис.5.2 Радиорелейная линия связи:
![]() и В
– оконечные станции;
и В
– оконечные станции;
![]() - промежуточные станции.
- промежуточные станции.
Каждый участок радиорелейной линии связи можно рассматривать как простейшую линию связи.
Для научных исследований часто применяют вторичные линии связи, в которых изучаемый сигнал облучает некоторое инородное тело (метеор, дождевое облако и др.), что приводит к рассеянию радиоволны. Среди рассеянных радиоволн найдется волна, которая дойдет до приемника (рис.5.3).
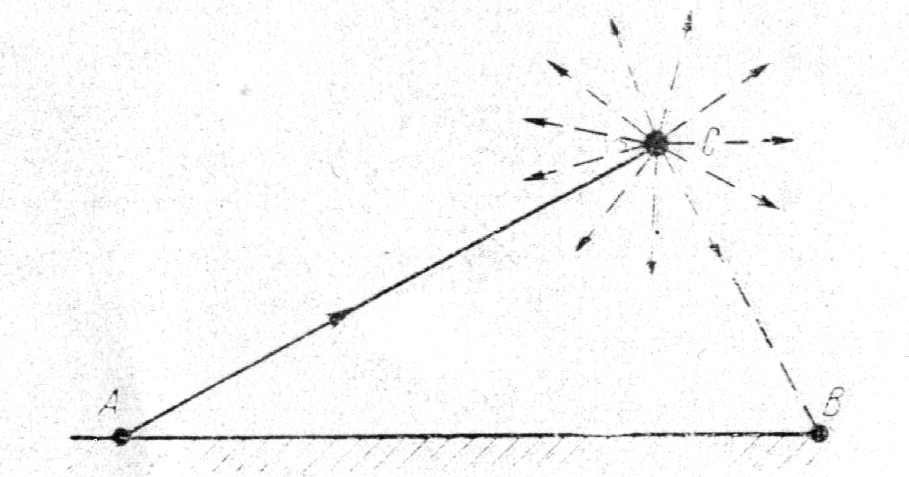
Рис 5.3 Вторичная радиолиния:
А – передатчик, В – приемник, С – облучаемый объект.
Радиоволны можно классифицировать по способу распространения. Такое основание классификации позволяет выделить следующие типы волн.
Свободно распространяющиеся волны – это волны, траектория которых близка к прямолинейным траекториям.
Земные волны – это волны, распространяющиеся в непосредственной близости от поверхности Земли. Земные волны также называются поверхностными волнами. Они способны частично огибать поверхность Земли за счет явления дифракции.
Тропосферные волны – это волны, распространяющиеся на значительные расстояния (до ≈ 1000 км) за счет рассеяния их в тропосфере и направляющего (волноводного) действия тропосферы. Напомним, что тропосфера – это нижний слой атмосферы. Верхняя граница тропосферы соответствует ≈ 15 км, характерная особенность такой границы заключается в постоянстве температуры, т.е. grad T=0. Тропосферными волнами распространяются волны, длина волны которых λ<10 м.
Ионосферные волны - это волны, распространяющиеся на большие расстояния и огибающие земной шар за счет многократного отражения от ионосферы. Ионосферными распространяются волны, длина волны которых λ>10 м, т.е. к ионосферным волнам относят волны КВ, СВ, ДВ и СДВ диапазонов. Следует иметь в виду, что метровые волны также могут распространяться как ионосферные – за счет рассеяния на неоднородностях ионосферы и отражений от метеорных следов.
5.2. Распространение радиоволн в свободном пространстве
Пусть в свободном
пространстве (однородной непоглощающей
среде с ε=1,μ=1) помещен точечный излучатель,
к которому подведена мощность
![]() .
Такой излучатель равномерно во все
стороны пространства излучает энергию,
волновая поверхность распространяющейся
волны представляет собой сферическую
поверхность (рис.5.4).
.
Такой излучатель равномерно во все
стороны пространства излучает энергию,
волновая поверхность распространяющейся
волны представляет собой сферическую
поверхность (рис.5.4).

Рис.5.4. Сферический фронт волны от точечного излучателя.
После начала излучения волны радиус сферического фронта будет иметь значение r. Распространяясь, волна переносит энергию, плотность потока которой через единичную площадку за единицу времени (модуль вектора Пойнтинга) определяется формулой:
![]() ,
,
![]() (5.1)
(5.1)
где
![]() - подведенная к излучателю мощность,r
– радиус
сферической волны.
- подведенная к излучателю мощность,r
– радиус
сферической волны.
Среднее значение плотности потока энергии за период времени Т находится:
![]() ,
,
![]() (5.2)
(5.2)
где
![]() -действующее
значение напряженности электрического
поля,
-действующее
значение напряженности электрического
поля, ![]() -действующее
значение напряженности магнитного
поля.
-действующее
значение напряженности магнитного
поля.
Связь между действующими значениями напряженностей электрического и магнитного полей выражается формулой:
![]() (5.3)
(5.3)
где ![]() -волновое
сопротивление свободного пространства,
определяемое, как известно,
-волновое
сопротивление свободного пространства,
определяемое, как известно,
![]() Ом.
Ом.
Исходя из формул (5.2, 5.3) можно для модуля вектора Пойнтинга записать:
![]() ,
,
![]() (5.4)
(5.4)
В нашем случае речь идет об одном и том же процессе излучения электромагнитной энергии точечным источником, поэтому на основании (5.1) и (5.4) запишем:
![]() (5.5)
(5.5)
Из равенства (5.5) определим:
![]() (5.6)
(5.6)
где
![]() - подведенная к излучателю мощность,r
– расстояние,
- подведенная к излучателю мощность,r
– расстояние,![]() -действующее
значение напряженности электрического
поля.
-действующее
значение напряженности электрического
поля.
В реальных условиях трассы в пунктах передачи используют антенны, предназначенные для концентрации излучаемой энергии в определенном направлении, т.е. служащие направленному излучению волны. Для учета направленных свойств антенны ввели параметр – коэффициентом направленного действия (КНД), выражающий степень направленности. Обозначим КНД через D. Все параметры, относящиеся к передающим устройствам, будем снабжать индексом 1, к приемным устройствам – индексом 2. Например, мощность подводимую к излучающей антенне в пункте передачи обозначим Р1, коэффициент ее направленности – Д1, Соответствующие обозначения для приемной антенны будут Р2, Д2.
Определим содержательную сторону введенного параметра КНД. Предположим, что рядом расположены две антенны: направленная А и всенаправленная В. На рис.5.5 показаны схематично диаграммы направленности обеих антенн.

Рис.5.5. Диаграммы направленности антенн, направленной (А) и изотропной (В).
Пусть к обеим
антеннам подводятся одинаковые мощности
![]() .
Очевидно, что в пункте приема, находящемся
на достаточно удаленном и одинаковом
для обоих случаев расстоянии r0,
напряженность поля, идущего от направленной
антенны будет больше по сравнению с
ненаправленной. Это обусловлено
концентрацией энергии направленной
антенной в требуемом направлении. Для
того чтобы получить такую же напряженность
поля, но от изотропного излучателя
(всенаправленной антенны), необходимо
увеличить мощность
.
Очевидно, что в пункте приема, находящемся
на достаточно удаленном и одинаковом
для обоих случаев расстоянии r0,
напряженность поля, идущего от направленной
антенны будет больше по сравнению с
ненаправленной. Это обусловлено
концентрацией энергии направленной
антенной в требуемом направлении. Для
того чтобы получить такую же напряженность
поля, но от изотропного излучателя
(всенаправленной антенны), необходимо
увеличить мощность
![]() ,
подводимую к антенне.
,
подводимую к антенне.
Коэффициент направленного действия (КНД) показывает во сколько раз необходимо увеличить мощность, подводимую к изотропному излучателю, чтобы получить такую же напряженность поля в пункте приема, как создаваемую направленной антенной.
КНД является безразмерной величиной. В дальнейшем покажем, что КНД измеряют в децибелах (дБ). Учитывая направленность передающей антенны, формула действующего значения напряженности поля примет вид:
![]() ,
,
![]() (5.7)
(5.7)
Амплитудное значение напряженности поля, пришедшего в пункт приема находится соответственно:
![]() ,
,
![]() (5.8)
(5.8)
Мгновенное значение напряженности электрического поля, т.е. значение поля, принимаемого в данный конкретный момент времени определяется:
![]() ,
,![]() (5.9)
(5.9)
где
r
– расстояние,
![]() - волновое число,с
– скорость света, ω
– циклическая частота,
- волновое число,с
– скорость света, ω
– циклическая частота,
![]() - мощность, подводимая к передающей
антенне,
- мощность, подводимая к передающей
антенне,![]() -КНД передающей
антенны.
-КНД передающей
антенны.
Мгновенное значение напряженности электрического поля можно записать в комплексной форме:
![]() ,
,
![]() (5.10)
(5.10)
В приведенных выше
формулах (5.7 – 5.10) физические величины
измеряются в международной системе
измерения СИ. Для практических расчетов
расстояние лучше измерять в километрах,
а не метрах, мощность – в киловаттах, а
не ваттах. Поэтому, выражая мощность
![]() в киловаттах
в киловаттах![]() ,
расстояниеr
в километрах
,
расстояниеr
в километрах
![]() ,
получим напряженность поля
,
получим напряженность поля![]() ,
выраженную в милливаттах на метр(мВ/м).
Учитывая введенные единицы измерения,
в формулах напряженности поля числовой
коэффициент изменит свое значение.
Итак, для практических расчетов
действующего значения распространения
радиоволн в свободном пространстве при
напряженности электрического поля
применяем формулу:
,
выраженную в милливаттах на метр(мВ/м).
Учитывая введенные единицы измерения,
в формулах напряженности поля числовой
коэффициент изменит свое значение.
Итак, для практических расчетов
действующего значения распространения
радиоволн в свободном пространстве при
напряженности электрического поля
применяем формулу:
![]() ,
,
![]() (5.11)
(5.11)
Для амплитудного значения напряженности электрического поля формула примет вид:
![]() ,
,
![]() (5.12)
(5.12)
Единицы измерения входящих в формулы (5.11), (5.12) физических величин записаны в виде индексов. Передающая и приемная антенна расположены на плоской поверхности земли на расстоянии r между собой.
Покажем простейшую радиотрассу в виде схемы (рис.5.6)

Рис.5.6. Схема простейшей радиотрассы.
Необходимо
определить значение мощности, поступающей
на вход приемника. Очевидно, что для
определения требуемой мощности необходимо
знать модуль вектора Пойнтинга, пришедшего
в раскрыв приемной антенны
![]() и учесть площадь раскрыва антенны, с
помощью которого «собирается» вся
приходящая энергия волны. Предварительно
введем понятиеэффективной
площади антенны
и учесть площадь раскрыва антенны, с
помощью которого «собирается» вся
приходящая энергия волны. Предварительно
введем понятиеэффективной
площади антенны
![]() ,которая
в антенно-фидерной технике определяется
формулой:
,которая
в антенно-фидерной технике определяется
формулой:
![]() (5.13)
(5.13)
где ![]() -КНД приемной
антенны, λ
– длина волны.
-КНД приемной
антенны, λ
– длина волны.
Плотность потока
энергии, поступающей в раскрыв антенны
![]() ,определим
на основании формулы (5.1), т.е.
,определим
на основании формулы (5.1), т.е.
![]()
Тогда мощность, поступающая на вход приемного устройства, определяется:
![]() ,
,
![]() (5.14)
(5.14)
При проектировании радиолиний удобно пользоваться понятием о потерях энергии, происходящих при распространении. Потери энергии определяются формулой:
![]() (5.15)
(5.15)
где
индекс св
указывает,
что речь идет о потерях при распространении
в свободном пространстве. Исключим
влияние антенн, т.е. положим![]() (обе антенны являются изотропными
излучателями). Тогда из формулы (5.15)
получимосновные
потери
энергии, связанные исключительно только
с распространением в свободном
пространстве.
(обе антенны являются изотропными
излучателями). Тогда из формулы (5.15)
получимосновные
потери
энергии, связанные исключительно только
с распространением в свободном
пространстве.
![]() (5.16)
(5.16)
Потери энергии выражают обычно в децибелах (дБ) на основании формулы:
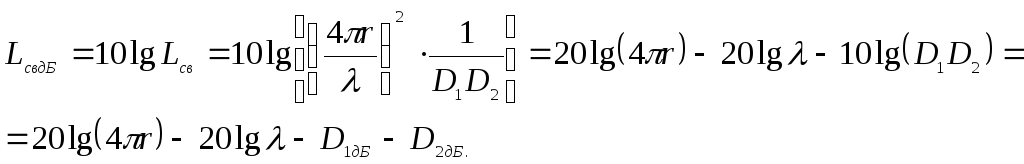
Таким образом,
получим формулу ![]()
![]()

![]() (5.17)
(5.17)
Из формулы (5.17) видно, что направленность антенны КНД выражают в дБ. В практических расчетах любое математическое отношение можно выразить децибелах. Для КНД выраженное в децибеллах следует использовать формулу:
![]() дБ,
(5.18)
дБ,
(5.18)
где
![]() - мощность, равная одному ватту, т.е.
- мощность, равная одному ватту, т.е.![]() =1Вт.
Тогда отношение
=1Вт.
Тогда отношение![]() получается
безразмерной величиной.
получается
безразмерной величиной.
Рассмотрим пример.
Определить величину основных потерь при распространении электромагнитной волны в свободном пространстве в случаях:
а) длина волны
![]() м
и расстояние между пунктами связиr=10
км;
м
и расстояние между пунктами связиr=10
км;
б) длина волны
![]() см
и расстояние между пунктами связиr=
см
и расстояние между пунктами связиr=![]() км.
км.
Решение: для определения величины основных потерь используем формулы
![]()
![]() Расчеты показали
следующие значения основных потерь:
Расчеты показали
следующие значения основных потерь:
а)
![]() =39,3
или
=39,3
или![]() =15,9
дБ;
=15,9
дБ;
б)
![]() =
=![]() или
или![]() =252
дБ.
=252
дБ.
Из полученных значений можно сделать вывод, что логарифмическая шкала является более удобной в использовании, т.к. имеет существенно меньшие пределы изменения значений.
При распространении радиоволн в реальных условиях необходимо обратить внимание на поглощение энергии волны и другие потери. Например, в процессе распространения земной волной происходят потери за счет частичного проникновения волны в толщу земной поверхности. Поэтому для учета ослабления поля радиоволны в реальных условиях вводится множитель ослабления F. В этом случае расчет действующего значения напряженности поля в пункте приема производится по формулам:
![]() ,
,
![]() (5.19)
(5.19)
где F – множитель ослабления, r – путь, проходимый волной от пункта передачи до приемного пункта. Таким образом, определить действующее значение напряженности поля на конце радиолинии можно, если будем знать значение множителя ослабления. Задача определения множителя ослабления F является главной при проектировании радиолиний.
Для расчета любой трассы необходимо правильно выбрать метод расчета множителя ослабления. В дальнейшем рассмотрим некоторые методы расчета радиотрасс.
Широко применяются радиоволны, распространяющиеся земной волной. Прежде чем приступить к изучению метода расчета множителя ослабления F для таких радиолиний, обратим внимание на особенности земной поверхности с точки зрения распространения радиоволн.
5.3. Учет электродинамических параметров земной поверхности
Распространение земных радиоволн происходит непосредственно вблизи поверхности, которая весьма разнообразна. Это может быть и морская поверхность, и пустыня, и лес, и застроенный город и др. С точки зрения электродинамики любая среда характеризуется относительной диэлектрической проницаемостью ε, относительной магнитной проницаемостью μ и удельной проводимостью σ. В таблице 5.2 приведены значения электрических параметров различных видов земной поверхности.
Таблица 5.2 Электрические параметры различных видов земной поверхности[ ].

Из таблицы 5.2 видно, что электродинамические параметры среды ε и σ зависят от длины волны (частоты) используемого диапазона. Возникает вопрос: с точки зрения проводящих свойств при распространении радиоволн, какой средой является подстилающая поверхность? Как известно, все среды по свойству проводимости классифицируют на проводники, диэлектрики и полупроводники. Интересующий нас вопрос можно сформулировать в виде: что представляет собой конкретная подстилающая поверхность для радиоволны: проводящей, диэлектрической или полупроводящей поверхностью?
Ответ на поставленный вопрос найдем с помощью первого уравнения Максвелла, которое для полупроводящей среды имеет вид:
![]()
Положим, что
напряженность электрического поля
изменяется по гармоническому закону в
виде
![]()
Выразим напряженность
электрического поля ![]() через производную
по времени:
через производную
по времени:
![]()
Подставляя ![]() в первое уравнение
Максвелла, получим:
в первое уравнение
Максвелла, получим:
![]() (5.20)
(5.20)
Как известно, для диэлектрической среды уравнение Максвелла имеет вид:
![]() (5.21)
(5.21)
Сравнивая уравнения (5.20) и (5.21) отмечаем, что можно ввести абсолютную комплексную проницаемость в виде:
![]()
 (5.22)
(5.22)
которая играет роль диэлектрической проницаемости полупроводящей среды.
В расчетах удобно пользоваться относительной диэлектрической проницаемостью, которая определяется:
![]() ,
,
т.е. можно записать
![]() ,
(5.23)
,
(5.23)
где λ – длина волны, ε – относительная диэлектрическая проницаемость, σ – удельная проводимость.
Напомним, что
плотность тока смещения определяется
![]() ,
плотность тока проводимости
,
плотность тока проводимости![]() .
.
При распространении радиоволны над конкретной поверхностью Земли необходимо знать, какие из плотностей токов (смещения или проводимости) в ней преобладают. Найдем отношение:
![]() ,
или
,
или
![]() (5.24)
(5.24)
На основании (5.24) можно классифицировать вид подстилающей поверхности следующим образом:
если
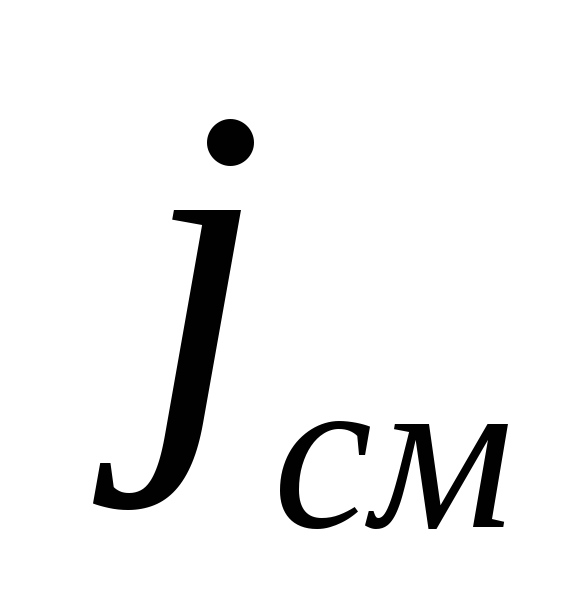 >>
>> ,
т.е. ε >> 60λσ, то подстилающая поверхность
является диэлектриком;
,
т.е. ε >> 60λσ, то подстилающая поверхность
является диэлектриком;если
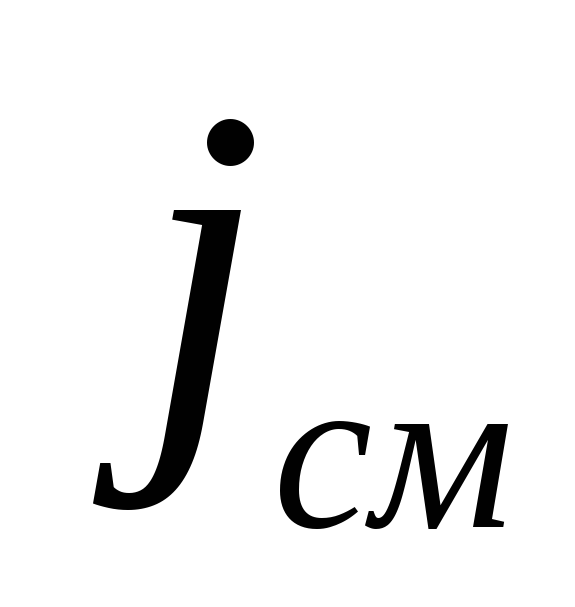 <<
<< ,
т.е. ε << 60λσ, то поверхность является
проводником (проводящей поверхностью);
,
т.е. ε << 60λσ, то поверхность является
проводником (проводящей поверхностью);если
 ≈
≈ ,
то поверхность является полупроводящей.
,
то поверхность является полупроводящей.
Таким образом, чтобы выяснить над какой поверхностью происходит распространение радиоволн, необходимо сравнить между собой ε и 60λσ.
Расчет радиотрассы УКВ диапазона земной волной над плоской поверхностью Земли
Наиболее простой метод расчета радиотрассы применяется в случае распространения радиоволн при небольших расстояниях между пунктами передачи. Причем поверхность Земли является плоской и однородной на протяжении всей трассы. Изучим метод расчета такой трассы для УКВ диапазона, в котором применяются поднятые антенны.
Поднятая антенна – это антенна, у которой фидерный (питающий) тракт не излучает и в высоту антенны укладывается несколько длин волн.
Рассмотрим трассу, схема которой показана на рис.5.7.

Рис.5.7. Схема радиотрассы УКВ диапазона.
Пусть в пункте
передачи А антенна поднята на высоту
![]() ,
в пункте приема В – на высоту
,
в пункте приема В – на высоту
![]() .
Б.А.Введенский в 1922 году предложил, что
в месте приема электромагнитное поле
можно рассматривать как интерференцию
двух лучей: прямого1
и отраженного от Земли 2.
Лучи, выходя из одного источника, являются
когерентными, поэтому в пункте В лучи
1 и 2 будут интерферировать между собой.
.
Б.А.Введенский в 1922 году предложил, что
в месте приема электромагнитное поле
можно рассматривать как интерференцию
двух лучей: прямого1
и отраженного от Земли 2.
Лучи, выходя из одного источника, являются
когерентными, поэтому в пункте В лучи
1 и 2 будут интерферировать между собой.
Действующую напряженность поля подсчитаем из известной ранее формулы:
![]() ,
,
![]() .
.
Задача сводится к нахождению множителя ослабления F.
Мгновенное значение напряженности поля прямого луча определяется:
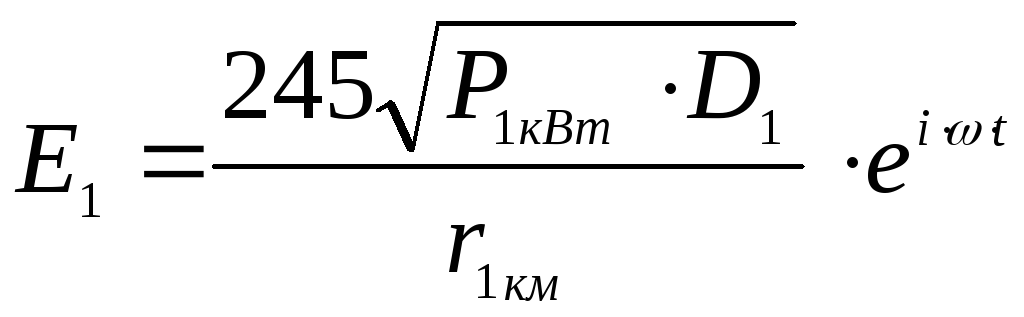 ,
,
![]() ,
(5.25)
,
(5.25)
Мгновенное значение напряженности поля для отраженного луча:
 ,
,
![]() ,
(5.26)
,
(5.26)
где
![]() - комплексный коэффициент отражения,
- комплексный коэффициент отражения,![]() - значение пути, проходимого отраженным
лучом,∆r
– разность хода между прямым и отраженным
лучом. Причем
- значение пути, проходимого отраженным
лучом,∆r
– разность хода между прямым и отраженным
лучом. Причем
![]()
Сделаем следующие ограничения:
Считаем, что высоты, на которые подняты антенны существенно меньше расстояния между начальным и конечным пунктами радиолинии, т.е.
 << r,
<< r,
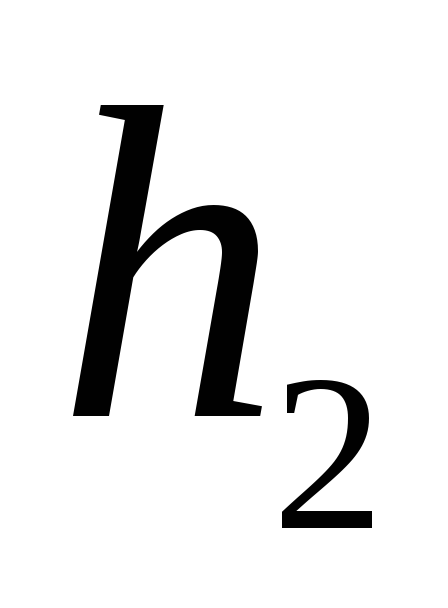 <<r,
где r
– расстояние между пунктами.
<<r,
где r
– расстояние между пунктами.Считаем, что лучи 1 и 2 излучаются передающей антенной почти в одном направлении. Коэффициенты направленности для обоих лучей имеют одно значение.
Учтем, что отраженный луч проходит больший путь, т.е. разность хода составляет
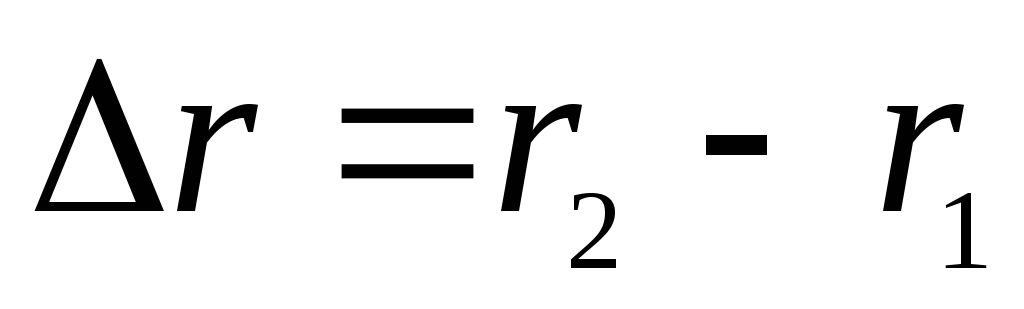 или набег фазы составляет
или набег фазы составляет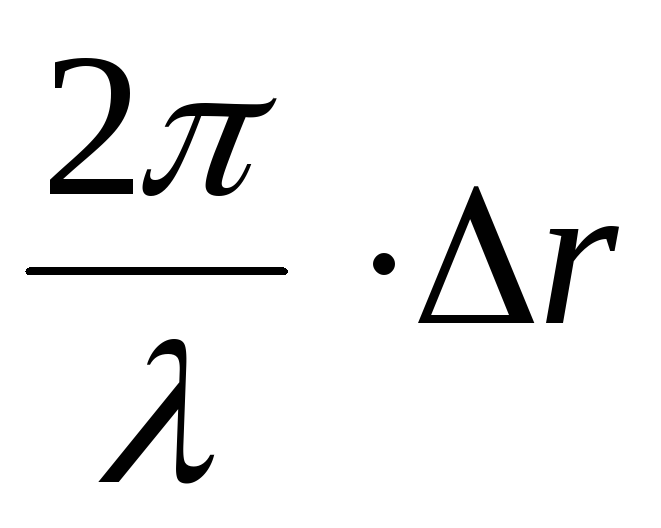 .
Кроме того, можно считать, что расстояния
.
Кроме того, можно считать, что расстояния .
Иными словами, расстояние, проходимое
каждым лучом, можно считать равным
расстоянию между пунктами А и В.
.
Иными словами, расстояние, проходимое
каждым лучом, можно считать равным
расстоянию между пунктами А и В.
Учитывая сделанные допущения, мгновенное значение напряженности результирующего поля в пункте В найдем:
![]() ,
,
![]() ,
(5.27)
,
(5.27)
где
![]()
![]() - угол изменения фазы при отражении,
- угол изменения фазы при отражении, ![]() -набег фазы за
счет разности хода прямого и отраженного
лучей.
-набег фазы за
счет разности хода прямого и отраженного
лучей.
В формуле (5.27) выполним преобразование сомножителя, стоящего в квадратных скобках:
![]()
где
![]()
Тогда формула (5.27) с учетом преобразования принимает вид:
![]()
![]() (5.28).
(5.28).
Сравнивая формулу
(5.28) с формулой
![]() заключаем, что множитель ослабленияF
определяется равенством:
заключаем, что множитель ослабленияF
определяется равенством:
![]() (5.29)
(5.29)
где
R
– коэффициент отражения, Θ – фаза
коэффициента отражения, ![]() -набег фазы за
счет разности хода между лучами.
-набег фазы за
счет разности хода между лучами.
Действующее значение напряженности результирующего поля определяется формулой:
![]()
![]() (5.30)
(5.30)
В эту формулу
входят три неизвестные величины: R
– модуль коэффициента отражения, Θ –
угол потери фазы при отражении, ![]() -разность хода
лучей.
-разность хода
лучей.
Из электродинамики известно, что R и Θ можно определить, если знать угол скольжения γ (рис.5.7). В [ ] показано, что угол скольжения определяется:
![]() (5.31)
(5.31)
где
![]() - высоты антенн,r
– расстояние между пунктами передачи
и приема.
- высоты антенн,r
– расстояние между пунктами передачи
и приема.
Там же доказано,
что разность хода ![]() определяется
выражением:
определяется
выражением:
![]() (5.32)
(5.32)
Из формулы (4.38)
видно, что множитель ослабления является
величиной переменной. В случае, когда
функция ![]() =1,значения множителя
ослабления являются максимальными
=1,значения множителя
ослабления являются максимальными
![]() ;
если
;
если![]() =-1,
то и множитель ослабления принимает
минимальные значения
=-1,
то и множитель ослабления принимает
минимальные значения
![]() .
Отсюда видно, что название множителя
ослабления носит условный характер. На
рис.5.8 показана зависимость множителя
ослабления от расстояния.
.
Отсюда видно, что название множителя
ослабления носит условный характер. На
рис.5.8 показана зависимость множителя
ослабления от расстояния.
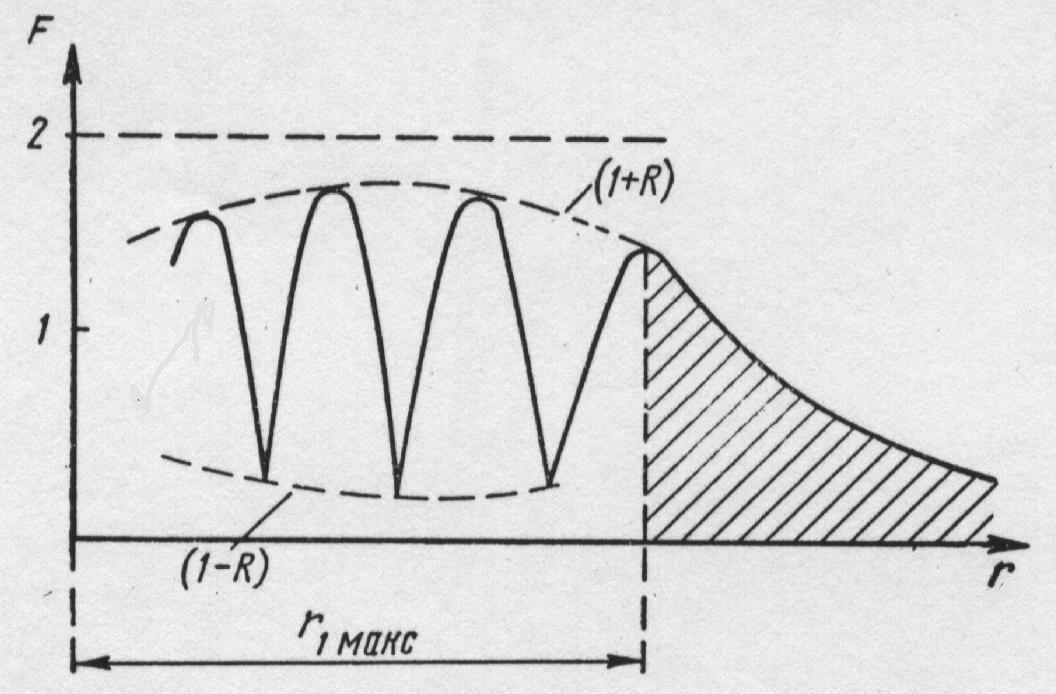
Рис.5.8. Зависимость множителя ослабления от расстояния при конечном значении коэффициента отражения.
Во многих случаях
формулу (5.29) можно упростить. Так, при
малых значениях угла скольжения γ для
большинства видов земной поверхности
коэффициент отражения можно принять
![]() ,
а угол потери фазы при отражении
,
а угол потери фазы при отражении![]() .
.
Принимая указанные
значения
![]() и
и![]() ,
можно после преобразования множителя
ослабления получить преобразованную
формулу множителя ослабленияF:
,
можно после преобразования множителя
ослабления получить преобразованную
формулу множителя ослабленияF:
![]()
 ,
(5.33)
,
(5.33)
Формула (5.33) также
характеризует интерференционную
структуру поля. Изменение расстояния
r,
как видно из формулы (5.33), приводит к
чередованию максимальных и минимальных
значений синуса. Можно определить такие
расстояния r
, на которых
![]() множитель
ослабления принимает только максимальные
или минимальные значения.
множитель
ослабления принимает только максимальные
или минимальные значения.
Максимальные значения множитель ослабления F достигает на расстояниях:
![]()
![]() (5.34)
(5.34)
где
n=0,1,2,…
Первый максимум наблюдается со стороны
больших расстояний, т.е.
![]()
Минимальное значение множителя ослабления F достигается на расстояниях:
![]()
![]() (5.35)
(5.35)
Первый минимум
расположен на расстоянии
![]() от передатчика.
от передатчика.
Из формулы (5.35)
видно, что максимальное значение
множителя ослабления соответствует
![]() ,
минимальное -
,
минимальное -![]() .
На рис.5.9 показан график зависимости
множителя ослабленияF
от расстояния при R=1.
.
На рис.5.9 показан график зависимости
множителя ослабленияF
от расстояния при R=1.

Рис.5.9. Зависимость множителя ослабления от расстояния при R=1.
Формулы для расчета напряженности поля в пункте приема называют интерференционными формулами.
Расчет радиотрасс СВ, ДВ, СДВ диапазонов при распространении земными волнами
Очевидно, что для диапазонов волн СВ, ДВ, СДВ , приведенный выше метод расчета неприемлем. Для таких диапазонов разработан иной метод расчета, учитывающий принципиальные особенности, свойственные именно перечисленным диапазонам. В чем заключаются эти особенности?
Установлено, что для перечисленных выше диапазонов свойственны следующие особенности:
1) при работе в СВ, ДВ, СДВ диапазонах применяются антенны, расположенные вблизи земной поверхности;
2) в перечисленных
диапазонах земная волна распространяется
над земной поверхностью, обладающей
проводящими свойствами, т.к. выполняется
неравенство ε
<< 60λσ. В
этом случае волна не может распространяться
в земной поверхности, следовательно,
вся энергия волны распространяется в
верхней полусфере. В результате значение
модуля вектора Пойнтинга увеличивается
в два раза, а напряженность поля в
![]() .
В этом случае действующее значение
напряженности поля для СВ, ДВ, СДВ
диапазонов определяется формулой:
.
В этом случае действующее значение
напряженности поля для СВ, ДВ, СДВ
диапазонов определяется формулой:
![]()

![]() (5.36)
(5.36)
Формула (5.36) называется формулой идеальной передачи или формулой Шулейкина-ван-дер-Поля.
Рассмотрим метод расчета действующего значения напряженности поля в пункте приема В, причем антенны расположены вблизи поверхности Земли (рис.5.10).
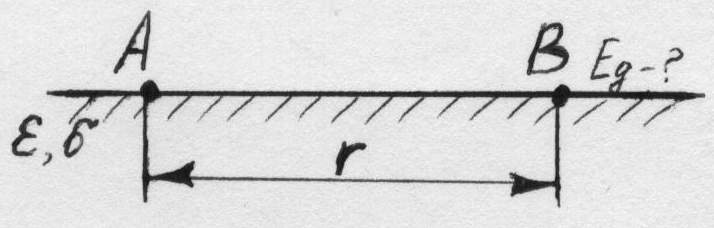
Рис.5.10. Схема радиотрассы земной волной для СВ-СДВ диапазонов.
В пункте передачи А непосредственно у поверхности земли расположена антенна передатчика. Вдоль поверхности, обладающей диэлектической проницаемостью ε и удельной проводимостью σ, распространяется электромагнитная волна. Для расчета напряженности поля по формуле (5.36) необходимо определить множитель ослабления.
Множитель ослабления F является функцией безразмерного параметра x, который иногда называют численным расстоянием и определяют:
 (5.37)
(5.37)
где
r
– расстояние между пунктами передачи
и приема, s
– масштаб расстояний,
![]() - комплексная диэлектрическая проницаемость
подстилающей поверхности,
- комплексная диэлектрическая проницаемость
подстилающей поверхности,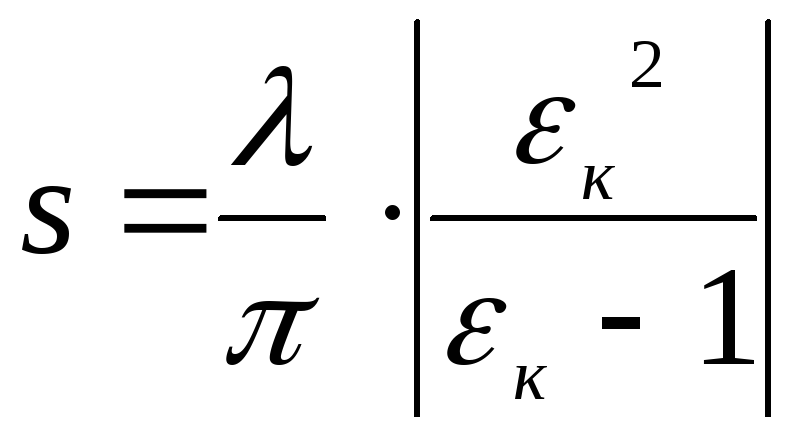 .
.
Подставляя значение относительной комплексной диэлектрической проницаемости, получим из формулы (5.37) значение x:
![]() (5.38)
(5.38)
В зависимости от вида поверхности формулу (5.38) можно видоизменить. В таблице 5.3 приведены конкретные виды поверхности и соответствующие каждой из них формулы расчета численного расстояния x.
Таблица 5.3. Формулы расчета численного расстояния x для различных видов
земной поверхности.
|
№ |
Вид поверхности |
Соотношение между параметрами поверхности |
Формула расчета численного расстояния x |
|
1
2
3 |
Диэлектрик
Проводник
Диэлектрик
|
ε >> 1
60λσ >> ε
ε >> 60λσ
|
|
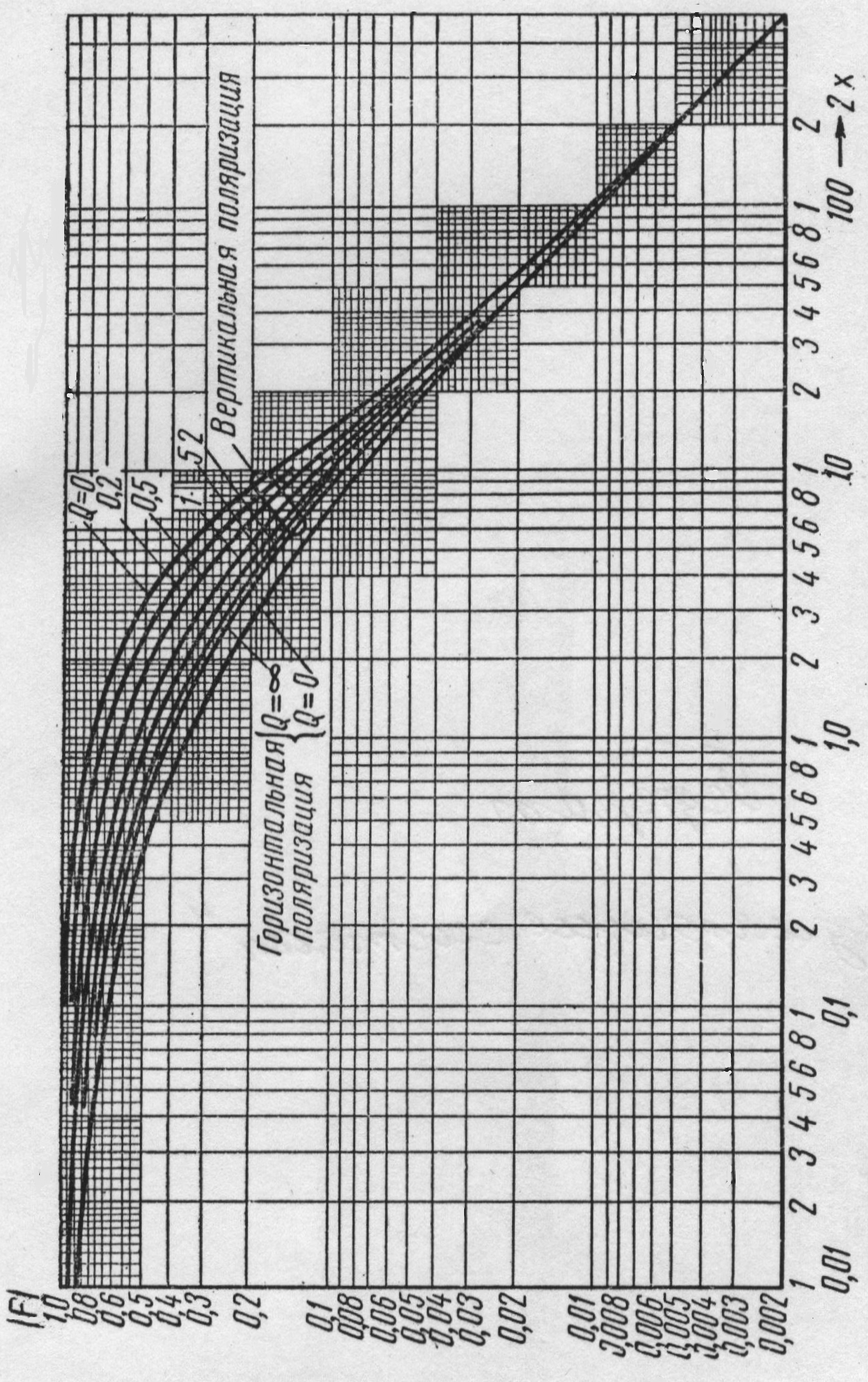
В приведенные формулы расчета x (таблица 5.3) необходимо подставлять значения входящих величин, измеренных в Международной системе СИ. Определив численное значение x, находят множитель ослабления F по графикам Берроуза, приведенным на рис. 5.11.
По оси абсцисс
отложены значения 2х,
по оси ординат – множитель ослабления
F.
Графики множителя ослабления приведены
для двух видов поляризаций: вертикальной
и горизонтальной при разном параметре
Q.
Параметр Q
определяет отношение плотности тока
смещения к плотности тока проводимости
![]() .
Изрис.5.11
видно, что при малых значениях х
все кривые стремятся к значению F=1.
Для значений х>25
кривые зависимостей множителя ослабления
сливаются.
.
Изрис.5.11
видно, что при малых значениях х
все кривые стремятся к значению F=1.
Для значений х>25
кривые зависимостей множителя ослабления
сливаются.
Если при расчете
![]() под руками не оказалось графиков
Берроуза, то множитель ослабленияF
можно вычислить по приближенной формуле:
под руками не оказалось графиков
Берроуза, то множитель ослабленияF
можно вычислить по приближенной формуле:
![]() (5.39)
(5.39)
где х – численное расстояние.
Если значение х>25, то формула (5.39) принимает вид:
![]() (5.40)
(5.40)
Формулой Шулейкина-ван-дер-Поля можно пользоваться при небольших расстояниях радиолинии, когда влиянием Земли можно пренебречь.
Сравнение результатов экспериментальных данных и выполненных теоретических расчетов позволило выявить ориентировочные значения максимальных расстояний, при которых применим расчет с помощью Шулейкина-ван-дер-Поля. В таблице 5.4 приведены эти значения расстояний.
Таблица 5.4. Максимальные расстояния, для которых применим метод
Шулейкина-ван-дер-Поля.
|
Диапазон волн, м |
Значение расстояний для середины диапазона, км |
|
200÷20000 50÷200 10÷50 |
300÷400 50÷100 10 |
Таким образом, для расчета радиотрассы диапазонов волн СВ, ДВ, СДВ необходимо применять метод Шулейкина-ван-дер-Поля.
Возникает вопрос: на какие расстояния могут распространяться земные волны? При каких условиях следует применять методы расчета земных волн? Для ответа на поставленные вопросы необходимо установить количественное соотношение, т.е. граничное условие применимости методов. К изучению поставленного вопроса перейдем с помощью определения расстояния прямой видимости.
Определение расстояния прямой видимости
Расстояние прямой видимости – это расстояние между пунктом передачи и приема радиоволн, определяемого по длине касательной, соединяющей эти пункты.
На рис.5.12 показано
расстояние прямой видимости
![]()
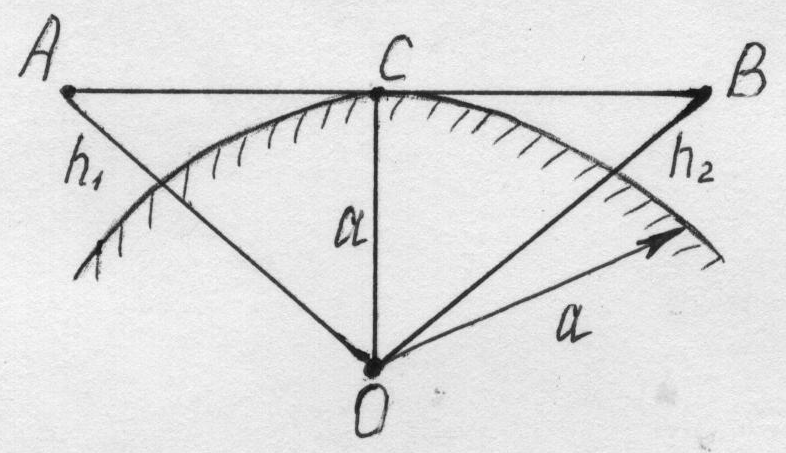
Рис.5.12. Схема для расчета расстояния прямой видимости.
Радиус Земли
обозначен а=6370
км, точка С
является точкой касания прямой АВ на
Земле. Высота передающей антенны
обозначена
![]() ,
высота приемной антенны
,
высота приемной антенны![]() .
Расстояния АС и СВ являются катетами
прямоугольных треугольников ∆АСО и
∆ОСВ.
.
Расстояния АС и СВ являются катетами
прямоугольных треугольников ∆АСО и
∆ОСВ.

Таким образом, расстояние прямой видимости определяется:
![]() (5.41)
(5.41)
где
а
– радиус Земли,
![]() ,
,![]() - высоты антенн.
- высоты антенн.
Входящие в формулу (5.41) величины измеряются в системе СИ. На практике радиус Земли удобно измерять в километрах. В этом случае формула (5.41) принимает вид:
![]()
 ,км(5.42)
,км(5.42)
Подчеркнем, что формула (5.42) позволяет рассчитать расстояние прямой видимости, выраженное в километрах.
Значение расстояния
прямой видимости ![]() позволяетустановить условие
применимости методов расчета радиотрассы
земными волнами.
позволяетустановить условие
применимости методов расчета радиотрассы
земными волнами.
Если длина
радиотрассы
![]() ,
то применим метод расчета трассы земной
волной для соответствующего диапазона
волн. Если расстояниеr
заключено в пределах
,
то применим метод расчета трассы земной
волной для соответствующего диапазона
волн. Если расстояниеr
заключено в пределах ![]() ,то такая область
называется зоной полутени. Если r>1,2
,то такая область
называется зоной полутени. Если r>1,2![]() ,то эта область
называется зоной тени. Для расчета
трассы, длина которой попадает в область
полутени и тени, применим дифракционный
метод расчета, т.к. происходит огибание
волнами поверхности Земли.
,то эта область
называется зоной тени. Для расчета
трассы, длина которой попадает в область
полутени и тени, применим дифракционный
метод расчета, т.к. происходит огибание
волнами поверхности Земли.
Представляет интерес распространение радиоволн в нижнем слое атмосферы – тропосфере, к изучению которого мы приступаем.
Влияние тропосферы на распространение земных волн
Тропосфера – это нижний слой атмосферы. Граница тропосферы простирается в полярных широтах до высоты 8-10 км, в тропиках - до 16-18 км. Тропосфера имеет постоянный относительный состав воздуха (только содержание водяных паров, зависящее от метеоусловий, резко уменьшается с высотой).
Важнейшее свойство тропосферы – убывание температуры с высотой, среднее значение градиента температуры составляет 5 град/км. Убывание температуры с высотой связано с тем, что тропосфера почти прозрачна для солнечных лучей, поэтому она пропускает лучи, которые нагревают земную поверхность. Нагретая поверхность Земли, являясь источником тепловой радиации, прогревает тропосферу снизу вверх.
Для тропосферы
вводят понятие нормальной
тропосферы,
т.е. тропосферы с параметрами, выражающими
среднее ее состояние. Нормальной
тропосфере приписывают следующие
параметры: у поверхности Земли давление
составляет Р=1013
мбар,
температура
![]() ,
относительная влажность воздухаS=60%.
Тропосферу можно рассматривать как
смесь газов: сухого воздуха и водяного
пара.
,
относительная влажность воздухаS=60%.
Тропосферу можно рассматривать как
смесь газов: сухого воздуха и водяного
пара.
С остояние
тропосферы описывается коэффициентом
преломления тропосферы, который для
нормальной тропосферы равенn=1,000325.
Видно, что таким значением пользоваться
неудобно (изменяются только последние
три цифры), поэтому ввели индекс
преломления, который определяется
соотношением:
остояние
тропосферы описывается коэффициентом
преломления тропосферы, который для
нормальной тропосферы равенn=1,000325.
Видно, что таким значением пользоваться
неудобно (изменяются только последние
три цифры), поэтому ввели индекс
преломления, который определяется
соотношением:
![]() ,
(5.43)
,
(5.43)
где n – коэффициент преломления.
Индекс преломления
для нормальной тропосферы составляет
![]() ,
т.е.N=325.
,
т.е.N=325.
Коэффициент преломления, соответственно, и индекс преломления зависят от состояния тропосферы. Для волн длиннее λ > 0,1 мм индекс преломления выражается формулой:
![]() (5.44)
(5.44)
где Т – температура, Р – давление, е – абсолютная влажность воздуха.
Индекс преломления,
как видно из формулы (5.44), изменяется с
высотой, т.к. меняется температура,
давление и содержание водяных паров.
Для нормальной тропосферы градиент
индекса преломления составляет
![]() ,
,![]() для практических расчетов используют
значение
для практических расчетов используют
значение
![]()
Тропосферу необходимо рассматривать как неоднородную диэлектрическую среду, коэффициент преломления n которой (значит и скорость распространения радиоволн) меняется с высотой. Т.к. тропосфера представляет собой неоднородную среду с меняющимся коэффициентом преломления, то ее можно рассмотреть как совокупность плоских слоев воздуха. Для каждого слоя имеется свое значение коэффициента преломления. Для двух соседних слоев коэффициенты преломления будут отличаться. В этом случае на границе раздела двух сред будет происходить явление преломления электромагнитных волн (рис.5.13).

Рис.5.13. Схема преломления радиоволны на границе раздела двух сред.
На основании явления преломления волна будет отклоняться от прямолинейного распространения. В результате преломления траектория волны искривляется. Для характеристики кривизны траектории вводят понятие радиуса кривизны траектории, который определяется
![]() (5.45)
(5.45)
где
![]() -градиент индекса
преломления.
-градиент индекса
преломления.
Формула (5.45) показывает, что радиус кривизны луча определяется не абсолютным значением коэффициента преломления, а быстротой изменения его с высотой. Знак минус в формуле (5.45) указывает, что радиус кривизны будет положительным, т.е. траектория будет обращена выпуклостью вверх, если коэффициент преломления уменьшается с высотой.
Для нормальной тропосферы радиус кривизны траектории составляет
![]()
Ранее мы, рассматривая распространение земных волн, предполагали, что они распространяются прямолинейно. В действительности, следует учитывать явление рефракции, приводящее к отклонению луча от прямолинейного распространения. Как учитывать рефракцию в реальных условиях распространения радиоволн?
Существует
упрощенный способ учета влияния
атмосферной рефракции. Суть предложенного
способа заключается в том, что хотя
электромагнитные волны в действительности
распространяются по криволинейным
траекториям, предположим, что
распространение происходит прямолинейно.
Причем, радиоволны распространяются
не над земной поверхностью, а над
некоторой воображаемой поверхностью,
имеющей эквивалентный радиус
![]() (рис.5.14).
(рис.5.14).
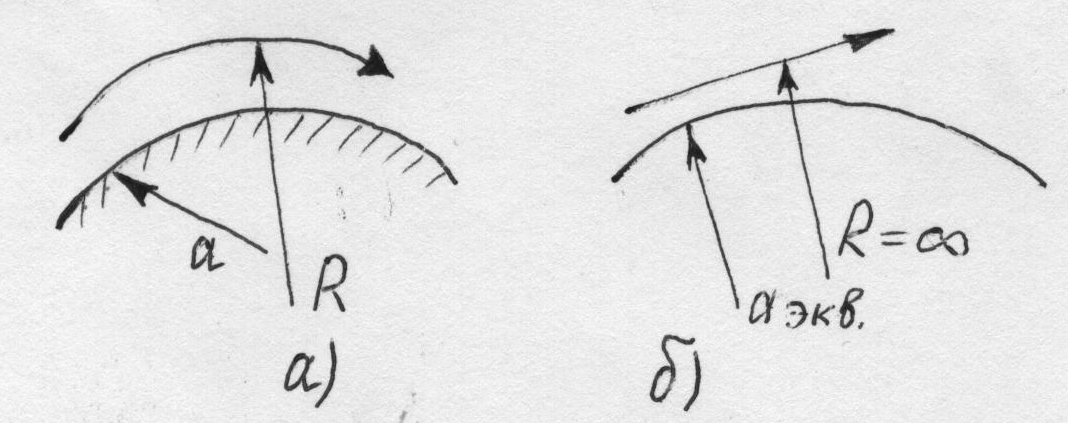
Рис.5.14. Траектория радиоволны:
а - реальная поверхность; б - воображаемая поверхность.
Введем понятие
относительной кривизны, которое
определяется
![]() ,
где a – радиус Земли, R - радиус кривизны
траектории. Определим эквивалентный
радиус
,
где a – радиус Земли, R - радиус кривизны
траектории. Определим эквивалентный
радиус![]() из условия равенства кривизны для
случаев а и б, изображенных на рис.51,
т.е. запишем равенство
из условия равенства кривизны для
случаев а и б, изображенных на рис.51,
т.е. запишем равенство
![]() (5.46)
(5.46)
где
а – радиус земной поверхности, R
– радиус траектории,
![]() - эквивалентный радиус поверхности, ∞
выражает радиус кривизны прямого луча.
- эквивалентный радиус поверхности, ∞
выражает радиус кривизны прямого луча.
Из равенства (5.46)
выразим
![]() :
:
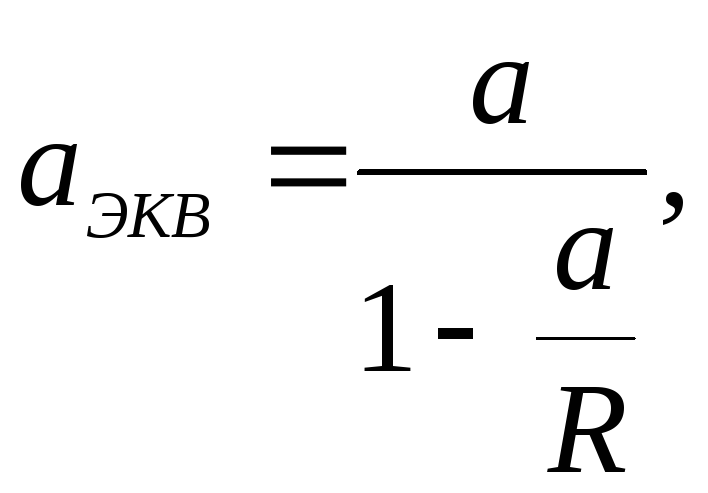 (5.47)
(5.47)
или

![]() .
(5.48)
.
(5.48)
Введем отношение эквивалентного радиуса к радиусу Земли:
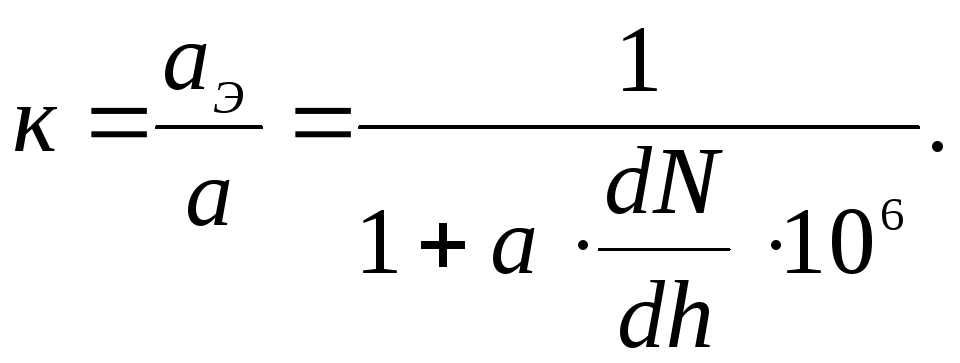 (5.49)
(5.49)
Для нормальной
тропосферы
![]() ≈8500км,
к=4/3.
≈8500км,
к=4/3.
Как реально учесть рефракцию в радиотрассе?
Прежде всего, рефракция учитывается при определении расстояния прямой видимости в этом случае формула расчета расстояния прямой видимости имеет вид
![]()

![]() .(5.50)
.(5.50)
Для нормальной атмосферной рефракции расстояние прямой видимости определяется выражением:
![]()
![]() (5.51)
(5.51)
Таким образом,
основные физические величины, с помощью
которых учитывается рефракция сводятся
к следующим:
![]()
Все перечисленные
величины зависят от градиента индекса
преломления ![]() ,который изменяется
в достаточно широких пределах. В
зависимости от значения градиента
,который изменяется
в достаточно широких пределах. В
зависимости от значения градиента ![]() рефракция проявляется
по-разному, поэтому рефракцию классифицируют
на три группы: отрицательную, нулевую
и положительную.
рефракция проявляется
по-разному, поэтому рефракцию классифицируют
на три группы: отрицательную, нулевую
и положительную.
Отрицательная
рефракция
– это
рефракция, при которой градиент индекса
преломления увеличивается, т.е. ![]() >0.
>0.
Положительная
рефракция
– это
рефракция, при которой градиент индекса
преломления уменьшается, т.е. ![]() <0.
<0.
Нулевая рефракция
– это
отсутствие рефракции, т.е.![]() =0.
=0.
В таблице 5.5 приведены основные характеристики разных видов рефракций.
Таблица 5.5. Классификация различных видов рефракции.
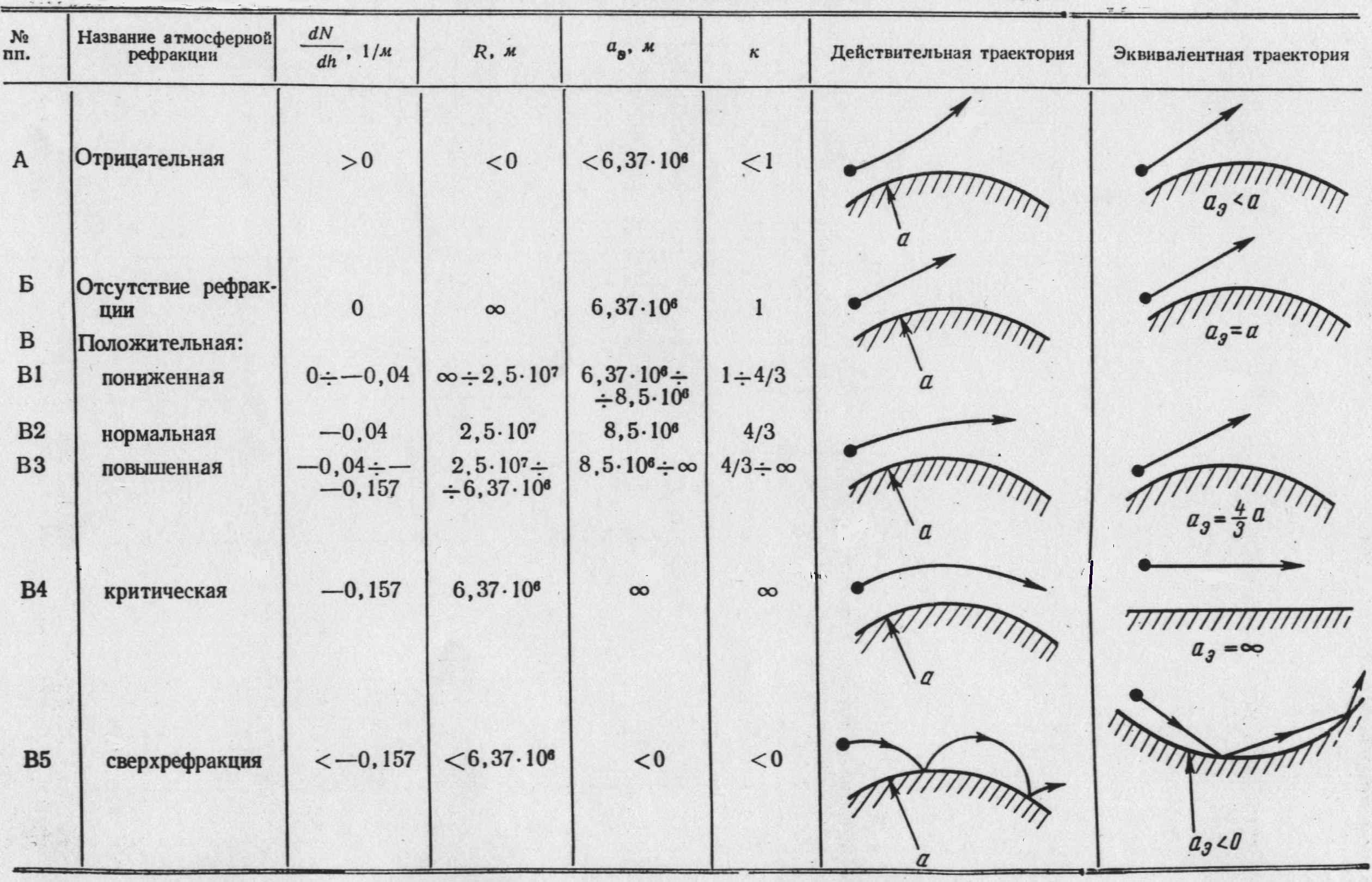
В таблице 5.5
приведены также действительные и
эквивалентные траектории радиоволн.
Отметим, что режим сверхрефракции
возникает в ограниченной области высот
тропосферы, где ![]() <-0,157
1/м, т.е. индекс
преломления убывает значительно быстрее,
чем при нормальной рефракции.
<-0,157
1/м, т.е. индекс
преломления убывает значительно быстрее,
чем при нормальной рефракции.
Распространение радиоволн в условиях пересеченной местности и при наличии препятствий
Ранее мы рассмотрели
методы расчета радиотрасс, проходящих
над плоской поверхностью Земли. В
реальных условиях типичным ландшафтом
материков является холмистая или
слабопересеченная местность. Степень
пересеченности местности определяется
соотношением между длиной волны λ и
высотой холмов
![]() .
Так, в условиях работы на ДВ и СВ диапазонах
слабопересеченную местность с высотой
холмов
.
Так, в условиях работы на ДВ и СВ диапазонах
слабопересеченную местность с высотой
холмов![]() можно считать гладкой поверхностью. В
диапазоне УКВ ту же местность следует
считать пересеченной.
можно считать гладкой поверхностью. В
диапазоне УКВ ту же местность следует
считать пересеченной.
В пересеченной местности холмы перекрывают область пространства, в которой происходит распространение электромагнитного поля, т.е. они экранируют область распространения электромагнитного поля, и тем самым вызывают эффект ослабления волны. Задача проектирования линии связи сводится к такому расположению антенн в пунктах передачи и приема, чтобы не происходило экранирования энергии поля.
Типичные условия, в которых проходит радиорелейная линия, показана на рис. 5.15.
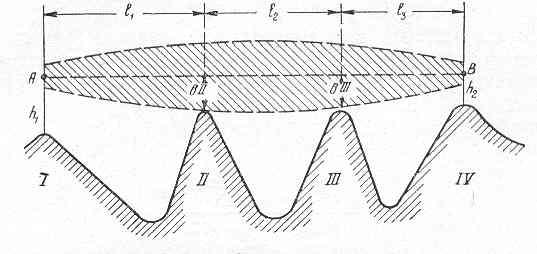
Рис. 5.15
Пусть пункт передачи размещен в точке А, пункт приема – в точке В, в промежуточных точках РРЛ, соответствующих C,D расположены смежные станции. Энергия волны, заключенная в заштрихованной области (рис. 5.15), представляет зону Френеля.
Обозначим через
![]() расстояния между холмов, тогда радиусы
первой зоны Френеля над точкамиC
и D
находятся из формул:
расстояния между холмов, тогда радиусы
первой зоны Френеля над точкамиC
и D
находятся из формул:
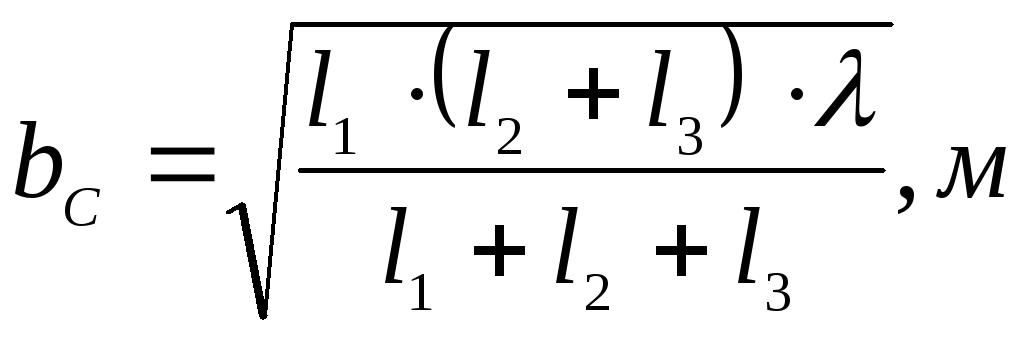 и
и 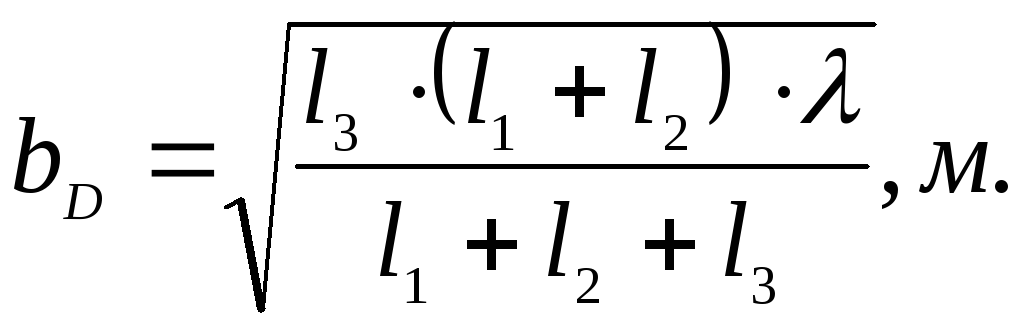
Высоты антенн в
пунктах А и В надо выбрать с таким
расчетом, чтобы «просветы» над холмами
C
и D
превышали значения ![]() и
и ![]() .
.
В практических расчетах следует учитывать сферичность Земли. Проще это можно сделать графическим методом. В основу построения положена формула для дальности горизонта, имеющая вид
![]() (5.52)
(5.52)
Формула (5.52) является уравнением параболы, по оси абсцисс х отсчитываются расстояния, по оси ординат y – высоты. Профиль гладкой поверхности Земли можно рассчитать по формуле:
![]() (5.53)
(5.53)
где r – общая длина линии связи.
В расчетах необходимо учитывать, что Земля с точки зрения геометрии является параболоидом вращения. Поэтому для учета кривизны поверхности Земли необходимо использовать масштабную сетку. На рис. 5.16 показана масштабная сетка для построения земной поверхности.

Рис. 5.16 Масштабная сетка для построения земной поверхности.
На сетку необходимо нанести профиль радиотрассы, с помощью которой можно определить необходимые высоты применяемых антенн для обеспечения зоны прямой видимости между пунктами А и В. Пример такого профиля трассы показан на рис. 5.17.

Рис. 5.17
На рис. 5.17 видно, что прямая АВ, проведенная между пунктом передачи и приема, проходит выше вершин холмов, расположенных на пути радиоволны.
Распространение радиоволн при наличии на пути экранирующих препятствий.
Пусть на пути между пунктами передачи и приема существует резко выраженное какое-либо препятствие. Рассмотрим случай, когда такое препятствие можно рассматривать в виде клиновидного непрозрачного препятствия.
На рис. 5.18 приведены примеры таких препятствий, возникающих на пути АВ.
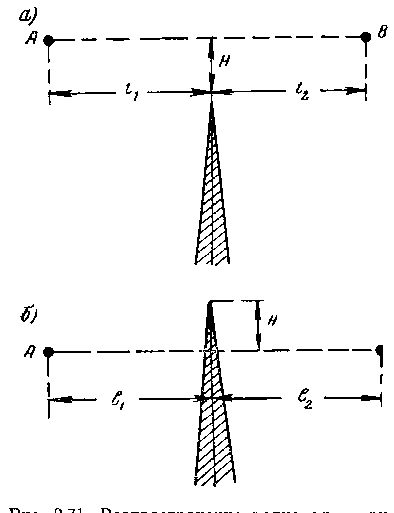
Н < 0
Н > 0
Рис. 5.18
На рис. 5.18а препятствие не пересекает прямую АВ, а только вклинивается в область пространства в которой распространяется основная часть энергии волны. На рис. 5.18б препятствие пересекает прямую АВ. Для разграничения таких случаев условились считать, что просвет Н будет принимать различные знаки, т.е. в случае рис. 5.18а просвет имеет отрицательный знак Н<0, в случае рис. 5.18б – положительный Н>0.
В расчете радиотрасс для таких случаев применяют теорию оптической дифракции. Множитель ослабления F рассчитывают по формулам:
![]() (5.54)
(5.54)
где
![]() а
а![]() и
и![]() -интегралы
Френеля, определяемые соответственно
по формулам
-интегралы
Френеля, определяемые соответственно
по формулам
 (5.55)
(5.55)
где
параметр
![]() - радиус первой зоны Френеля в месте
расположения препятствия,Н
– высота экрана, которая может принимать
положительные и отрицательные значения
(рис. 5.18).
- радиус первой зоны Френеля в месте
расположения препятствия,Н
– высота экрана, которая может принимать
положительные и отрицательные значения
(рис. 5.18).
Расчет множителя ослабления F по формулам (5.54) показывает, что зависимость от параметра v имеет вид, приведенный на рис. 5.19.

Рис. 5.19
Если параметр v>2, то множитель ослабления можно рассчитать по формуле
![]() (5.56)
(5.56)
Для расчета радиотрассы УКВ диапазона следует учесть следующие обстоятельства. На краю непрозрачного клиновидного экрана происходит дифракция. Причем дифрагирует не только прямая волна АВ, но и волны отраженные от поверхности Земли на участках между передающей антенной и экраном, и экраном и приемной антенной. Таким образом, в пункте приема В происходит сложение (интерференция) пришедших четырех волн: АМВ, А′МВ, АМВ′, А′МВ′. Здесь применен прием зеркального отображения.
В принципе может случиться, что фазовые соотношения приобретут такие значения, что напряженность поля в месте расположения приемной антенны будет в четыре раза превышать поле, созданное одним лучом.
Отметим, что форма встречаемых препятствий весьма многообразна и в настоящее время пока не создано надежных аналитических методов расчета радиотрасс.
Рекомендуемая литература
Долуханов М.П. Распространение радиоволн. – М.:Связь, 1972. -336 с.
Баскаков С.И. основы электродинамики. – М.:Сов. радио , 1973. -248 с.
Никольский В.В., Никольская Т.И. Электродинамика и распространение радиоволн. – М.: Наука, 1989. – 544 с.
Красюк Н.П., Дымович Н.Д. Электродинамика и распространение радиоволн. – М.: Высшая школа, 1974. -536 с.
Бредов М.М., Румянцев В.В., Топтыгин И.Н. Классическая электродинамика. –СПб.: Изд-во «Лань», 2003. – 400 с.
Головин О.В., Чистяков Н.И., Шварц В., Хардон Агиляр И. Радиосвязь. – М.: Горячая линия –Телеком, 2001. -288 с.
Петров Б.М. Электродинамика и распространение радиоволн. – М.: Радио и связь, 2000. -559 с.
Фальковский О.И. Техническая электродинамика. Учебник для вузов связи. – М.:Связь , 1978. - 432 с.
Гольдштейн Л.Д., Зернов Н.В. Электромагнитные поля и волны. . – М.:Сов. радио , 1971. - 664 с.