0. 2.2. Розподіл імовірностей дискретної випадкової величини

Нехай дискретна випадкова величина з областю визначення і областю значень . Для дискретної випадкової величини можна задати розподіл імовірностей, вказавши для кожного імовірність відповідної події і F, яка визначається співвідношенням

,

тобто

В результаті експерименту випадкова величина обов’язково набуде деякого значення , тобто це буде подія, яка неминуче відбувається при кожному випробуванні і вона є вірогідною. Тому для імовірностей виконується рівність норміровки

.

Розподіл імовірностей дискретної випадкової величини можна задавати також у вигляді таблиці:

Таблиця 2.1

				...		...
				...		...

або графічно у вигляді діаграми:

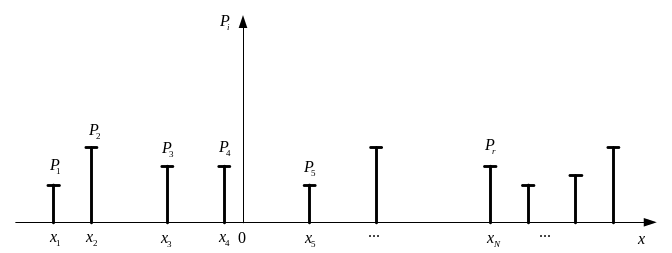
Рис. 2.1. Розподіл імовірностей дискретної випадкової величини

На діаграмі (рис. 2.1) по вісі абсцис, згідно з вибраним масштабом, відкладаються значення випадкової величини , а по вісі ординат – відповідні їм імовірності .

При застосуванні теорії імовірностей, у тому числі і при вирішенні задач статистичної обробки сигналів, найчастіше мають справу не з самими випадковими величинами, а з їх розподілами. Це пов’язано з тим, що, як правило, внаслідок експерименту реєструють значення випадкової величини, але не реєструється, яким елементарним наслідком закінчився саме випробування, тобто реєструються значення функції, а не значення аргументу.

Та обставина, що при різних випадкова величина може набувати одного і того ж значення, виявляється суттєвим: множина можливих значень випадкової величини може бути набагато простішою, ніж множина .

Приклад 2.3. Наведемо ряд розподілів найбільш вживаних на практиці дискретних випадкових величин. Позначимо .

1. Біноміальний розподіл

де - ціле додатне число,

2. Пуассонівський розподіл

℮ ,

3. Логарифмічний розподіл

4. Поліноміальний розподіл

де , - довільні цілі невід’ємні числа, що задовольняють умові

0. 2.3. Функція розподілу імовірностей випадкової величини

Для неперервної випадкової величини область її значень являє собою континуальну множину. Окрім того, імовірність – нормована міра. Тому апріорна імовірність окремого значення неперервної випадкової величини дорівнює нулеві і для неї ряд розподілу уже не відіграє тієї ролі, що і для дискретної випадкової величини. Взагалі, можна сказати, що для неперервної випадкової величини ряд розподілу не має сенсу.

Як же задавати розподіл імовірностей для неперервної випадкової величини? Вихід полягає в тому, що апріорна імовірність події „значення неперервної випадкової величини попадає в інтервал ” може бути відмінною від нуля. Тому при характеристиці імовірнісних властивостей неперервних випадкових величин, в тому числі і при заданні розподілу імовірностей, використовують „інтервальний” підхід. Його ідея полягає в тому, що для неперервної випадкової величини описують імовірності не окремих її значень, а задають імовірності попадання в інтервали. Зазначимо, що такий підхід може бути використаний і при імовірнісному описі дискретних випадкових величин. Тобто цей метод має у визначеному розумінні властивість універсальності.

Отже будемо вважати, що випадкова величина може набувати будь-яких дійсних значень, тобто . Це не призводить до заниження загальності розгляду, тому що в разі, коли область можливих значення випадкової величини є скінченим відрізком , то для відрізків числової вісі, що залишилися, тобто для подій і будемо вважати їх імовірності рівними нулю.

Розглянемо числову вісь (див. рис. 2. 2) і зафіксуємо деяке число .

Рис. 2.2. Числова вісь, що зображає область можливих значень

неперервної випадкової величини

Тоді область значень випадкової величини розділиться на дві частини: перша - і друга - . Розглянемо імовірність події „випадкова величина набула значення, що лежить в межах першого інтервалу” - . Очевидно, що числове значення цієї імовірності залежить від величини числа . Таким чином, ми можемо розглядати функцію

,

яка показує, як залежить від вибраного значення порогу імовірність того, що значення випадкової величини не перевищує його. Така функція має назву функція розподілу імовірностей випадкової величини (або просто функція розподілу).

Розглянемо основні властивості функції розподілу.

1. Із означення функції розподілу випливає, що не має фізичної розмірності (безрозмірна).

2. Функція є монотонною неспадною функцією, тобто при завжди .

3. - обмежена функція, тобто

.

4. - неперервна зліва, тобто

.

5. (неможлива подія);

(вірогідна подія).

5. Нехай і 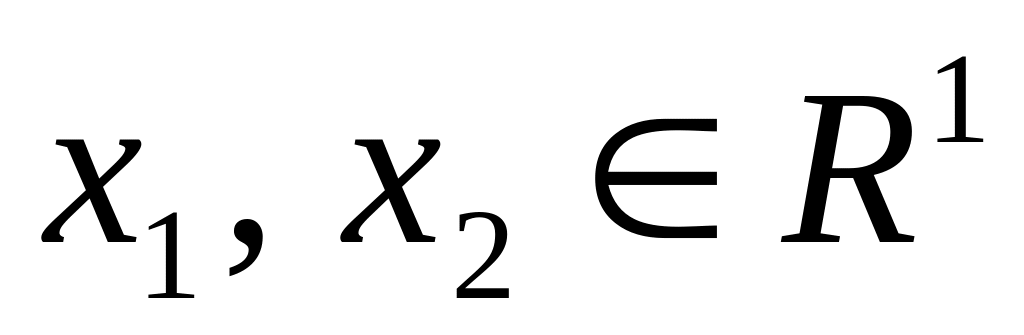(див. рис. 2.3). Розглянемо три події:

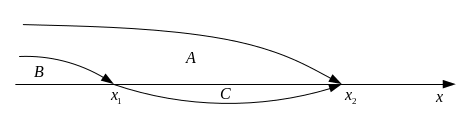
Рис. 2.3. До визначення імовірності події

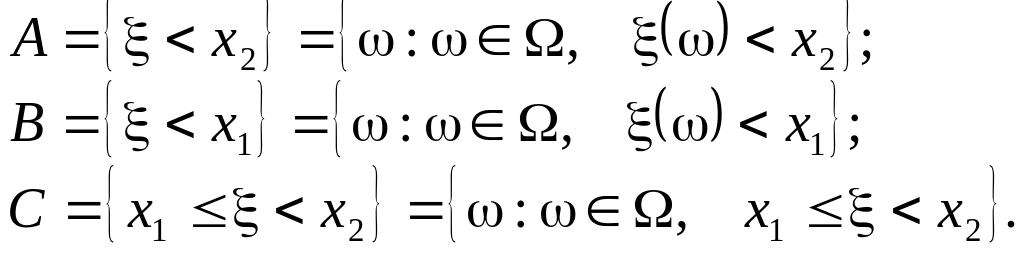
Події і несумісні, тобто і, окрім того,

Тому згідно з правилом додавання імовірностей

або

.

Але, за означенням функції розподілу ,

Остаточно маємо

,

тобто імовірність того, що випадкова величина в наслідок експерименту набуде значення, яке лежить в межах від до дорівнює приросту функції розподілу на інтервалі .

Для дискретної випадкової величини з областю значень функція розподілу для будь-якого може бути обчислена (якщо заданий ряд розподілу : ) за формулою

. (2.1)

Використовуючи одиничну функцію Хевісайда

праву частину формули (2.1) можна переписати так

.

Якщо відома функція розподілу дискретної випадкової величини, то можна розв’язати і обернену задачу, тобто за поданою функцією розподілу дискретної випадкової величини знайти імовірність того, що випадкова величина в наслідок експерименту набуде значення, яке дорівнює :

(2.2)

На рис.2.4 зображено графік функції розподілу деякої дискретної випадкової величини .

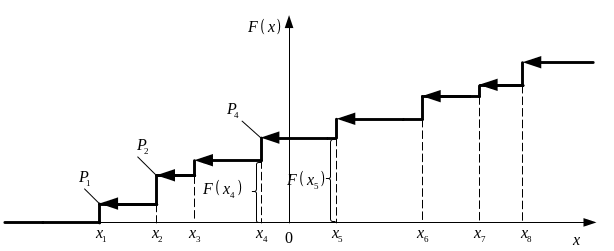
Рис. 2.4. Функція розподілу дискретної випадкової величини

Згідно з формулою (2.2), наприклад, для імовірності (див. рис. 2.4) маємо

.

Отже, функція розподілу для дискретної випадкової величини всюди постійна, за винятком точок її росту , які співпадають зі значеннями, яких може набувати випадкова величина. В цих точках змінюється стрибком на величину, яка дорівнює відповідній імовірності