Лабораторная работа №2 метод наименьших квадратов. Линейная зависимость

Очень часто исследуемая величина меняется с изменением условий опыта, а задача измерений состоит в нахождении функциональной зависимости, которая наилучшим образом описывает закон изменения интересующей на величины (например, зависимость объема газа от давления, вязкости жидкости от температуры и т.д.)

Положим, мы определяем некоторую величину y, зависящую только от величины x. Для каждого значения x_i проводим одно или несколько измерений и получаем соответствующие значения y_i. Чаще всего y_i известна не точно, а с определенной погрешностью ∆y_i. Также часто может быть неизвестно и точное значение x_i. Этот массив данных позволяет с некоторой степенью вероятности определить ту функциональную зависимость, которой связаны x и y, y = f(x). Однако таких функций можно брать бесчисленное множество. Для выбора единственной используем принцип простоты и монотонности зависимости.

Эта задача может быть решена с помощью метода наименьших квадратов. Суть метода состоит в нахождении таких значений параметров, входящих в искомую функциональную зависимость, при которых сумма квадратов отклонений значений функции от экспериментальных данных будет минимальной.

Рассмотрим особенности метода наименьших квадратов на примере линейной зависимости в случае одной переменной. Пусть искомая функция является линейной, т.е. , где a и b неизвестны, а x и y заданы некоторыми значениями (x_i, y_i), полученными в результате некоторого эксперимента. При подстановке значений в уравнение получаем . Разность называется невязкой и возникает в результате в результате ошибок эксперимента, ошибок вычислений, неточной линейной зависимости и т.п. Тогда требуется подобрать a и b так, чтобы сумма квадратов невязок, т.е была минимальной. Итак, – функция двух переменных и требуется найти ее минимум. Минимум этой суммы находится по правилам дифференциального исчисления. Это соответствует равенству нулю производных функции по a и b.

Отсюда, и . Эта система уравнений легко решается относительно a и b:

(2.1)

Теория дает возможность определить также дисперсию уклонения (количественно охарактеризовать степень разброса точек) и дисперсию коэффициентов a и b. Результаты расчета могут быть записаны в виде , ; , t_α – коэффициент Стьюдента, S_a и S_b – дисперсии коэффициентов. Степень приближения экспериментальной зависимости к прямой характеризуется коэффициентов r. Чем ближе значение r к единице, тем лучше экспериментальные данные описываются уравнением прямой, тем надежней интер- и экстраполяция.

В результате математических выкладок получаем систему, состоящую из двух уравнений с двумя неизвестными m и b.

и далее ,

где , , , – соответственно средние арифметические значения x_i, y_i, и x_iy_i [1].

Например, классическая задача для экспериментальной химии определение Аррениусовских параметров. Известно, что зависимость константы скорости реакции от абсолютной температуры, как правило, хорошо описывается при помощи эмпирического уравнения Аррениуса.

(2.2)

где k₀ – множитель (предэкспонента), который в простейших случаях может быть вычислен исходя из молекулярных представлений о механизме элементарного акта; E_a – энергия активации реакции; R – универсальная газовая постоянная; T – абсолютная температура. Значения k₀ и E_a, входящие в уравнение Аррениуса, находят из экспериментальных значений констант скорости реакции, измеренных при различных температурах.

Задача: Пользуясь экспериментальными данными о величине константы скорости химической реакции при различных температурах, найти значения предэкпоненциального множителя и энергии активации по формулам (2.1). Построить график и подобрать аппроксимирующую функцию с помощью встроенных функций программы Excel.

t, ^o	550	560	570	580	590	600	610	620	630
k10^5, c^-1	2,5	4,7	8,2	12,3	23,1	35,3	57,6	92,4	141,3

Прологарифмируем уравнение (2.2) чтобы получить линейную функцию:

Положим равными:

Составим в программе Excel таблицу (рис.9):

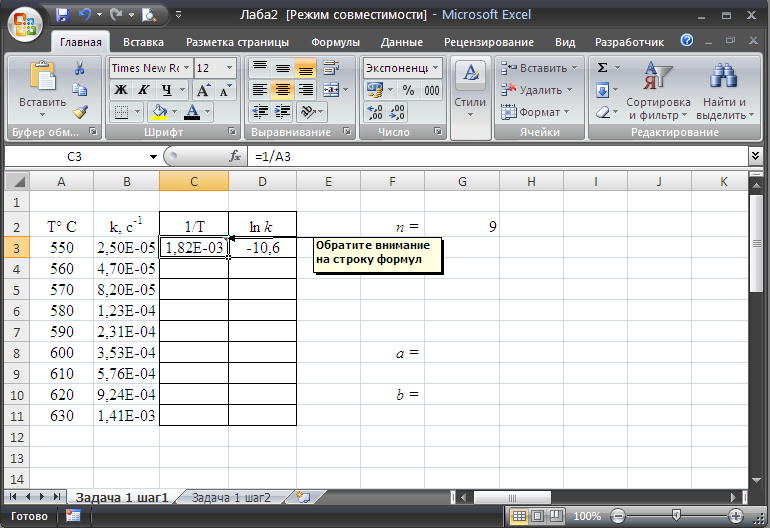
Рис. 9

Рассчитываем значения переменных для расчета a и b по формуле (2.1)

Рассчитываем значение постоянных параметров:

Строим график:

используя встроенные функции программы Excel:

Задача 1. Определение Аррениусовских параметров. Для реакции термического разложения этана получены следующие значения констант скоростей реакции первого порядка при разных температурах:

t, ^o	420	430	440	450	460	470	490	500	510
k10^5, c^-1	2,5	4,7	8,2	12,3	23,1	35,3	57,6	92,4	141,3

Постройте график зависимости lg k от 1/T. Рассчитайте энергию активации и предэкспоненциальный множитель, используя метод наименьших квадратов.

Задача 2. Определение гидратного числа для карбоновой кислоты. При изучении процесса экстракции карбоновой кислоты RCOOH из водного раствора с помощью органического растворителя обнаружилось, что в неводную фазу наряду с кислотой переходит некоторое количество воды, причем увеличение концентрации кислоты в неводной фазе сопровождается увеличением концентрации воды. Это дает возможность пред­положить, что при экстракции происходит образование гидросольвата вида RCOOH  x₁Н₂О  x₂Z, где Z — обозначение молекулы экстрагирующего вещества. Образование гидросольвата, протекающее по реакции:

RCOOH + х₁Н₂О + x₂Z = RCOOH  х₁Н₂О  x₂Z

предполагает наличие линейной зависимости между величинами концент­рации карбоновой кислоты х и воды у в органическом растворителе после экстракции: , где величины m и b представляют собой соответственно гидратное число карбоновой кислоты (число молекул воды на одну молекулу кислоты) и фоно­вую растворимость воды в используемом растворителе.

На основании результатов анализа органической фазы после экстракции из водного раствора, содержащего различное количество карбоновой кислоты определить гидратное число карбоновой кислоты.

мМRCOOH	4,0	7,0	9,4	10,8	13,0	16,0	18,4	20,0
мМH2O	11,2	14,6	16,6	17,6	19,6	22,4	24,6	26,6