2.11 Стійкість асиметричних криптосистем, що базуються на криптоперетвореннях в групі точок еліптичних кривих. Приклади розв’язку задач та задачі для самостійного розв’язання

2.11.1 Основні теоретичні відомості

В пошуках криптографічних алгоритмів з відкритим розповсюдженням ключів з експоненціальною складністю криптоаналізу спеціалісти зупинились на криптографічних перетвореннях, що виконуються в групі точок ЕК. Відповідно до прогнозів ці перетворення ще довго забезпечуватимуть необхідний рівень стійкості. Розглянемо основні задачі криптоаналізу для систем, в яких перетворення здійснюються в групі точок ЕК, методи їх розв’язання та дамо оцінку стійкості для відомих нам методів криптоаналізу.

Під час аналізу стійкості необхідно розглядати дві проблеми стійкості  розв’язання задачі дискретного логарифму та задачі Діффі-Хеллмана.

Проблема дискретного логарифму формується в наступному вигляді. Нехай задано точку G на еліптичній кривій E(F(q)), де q=p (p  просте число) або q=p^m (p  просте число, m  натуральне, mN). Відомо також значення відкритого ключа Q, причому

. (2.99)

Необхідно знайти конфіденційний (особистий) ключ d.

Проблема Діффі-Хеллмана формується в наступному вигляді. Нехай дано ЕК E(F(q)), відомо значення точки 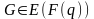, а також відкритий ключ . Необхідно знайти загальний секрет

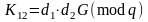, (2.100)

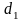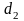
де та  особисті ключі відповідно першого та другого користувачів.

На сьогодні для аналізу стійкості та проведення криптоаналізу знайшли розповсюдження декілька методів Поларда 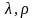 та оптимальний 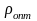. Розглянемо метод Поларда на прикладі ЕК над простим полем Галуа 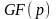, тобто

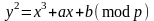. (2.101)

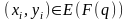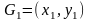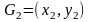Для всіх точок задано операції додавання та подвоєння. Наприклад, якщо , а , то

,

де

(2.102)

Для ЕК над полем 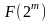виду

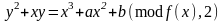, (2.103)

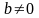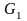причому , сума двох точок та

,

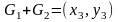де

(2.104)

примітивний поліном m-го ступеня;

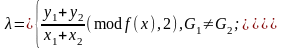(2.105)

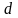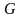
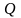
Для розв’язання задачі пошуку конфіденційного ключа в порівнянні (2.99) розглянемо -метод Поларда над простим полем . Нехай  базова точка,  відкритий ключ, шукатимемо пари цілих 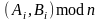та 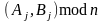, таких що

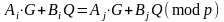. (2.106)

Позначимо в загальному вигляді

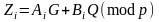. (2.107)

Суть -методу Поларда розв’язання порівняння (2.99) заключається в наступному. Знайдемо деяку функцію 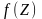, вибравши , де  порядок точки на ЕК

. (2.108)

Далі знайдемо послідовність:

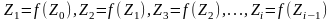
для пар 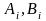, таких що:

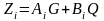. (2.109)

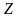Рекомендується в простих випадках (при відносно невеликих ) послі-довність розраховувати у вигляді:

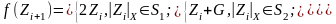(2.110)

При цьому 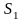, 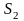та 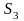складають частини області 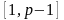. Якщо область рівномірно ділиться, то (2.11.12) має вигляд:

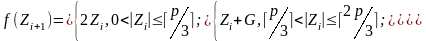(2.111)

При побудові множини 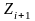пошук буде успішним, якщо ми знайдемо

,

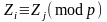що еквівалентно знаходженню

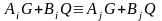. (2.112)

Зробивши прості перетворення, маємо:

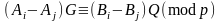(2.113)

і далі

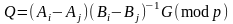. (2.114)

З (2.99) та (2.114) випливає, що

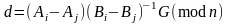, (2.115)

.

Більш ефективним є розрахунок з розбиванням інтервалу на інтервалів. Для реальних значень рекомендується 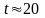. В цьому випадку замість (2.110) маємо

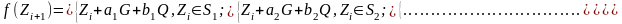(2.116)

причому та 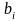є випадкові цілі із інтервалу .

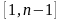У випадку (2.116) рішення знаходиться як і раніше у вигляді (2.111), а потім (2.115). З урахуванням позначень в (2.116)

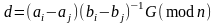. (2.117)

Успішне розв’язання задачі дискретного логарифму в групі точок ЕК вимагає

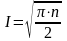(2.118)

операцій на ЕК.

Із (2.117) та (2.118) випливає, що задачу пошуку пар 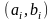та 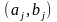може бути розпаралелено на 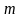процесів, тоді

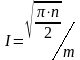. (2.119)

Розроблено методику та алгоритми, які дозволяють розв’язати задачу (2.99) зі складністю

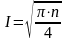, (2.120)

а при розпаралелюванні на процесорах складність визначається, як

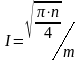. (2.121)

При розв’язанні задачі важливо правильно (вірніше успішно) вибрати 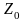. Значення рекомендується вибирати у вигляді

.

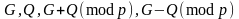також можна вибирати як

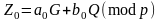, (2.122)

де .