
- •6.4.1 Оцінка автентичності захисту інформації з використанням симетричних алгоритмів. Приклади розв’язку задач та задачі для самостійного розв’язання
- •Ми застосуємо в оцінці відповідне більше, так як не доведено, що в режимі виробки імітоприкладки забезпечується досконала автентичність.
- •1.12 Оцінка автентичності інформації, захищеної з використанням асиметричних алгоритмів. Приклади розв’язку задач та задачі для самостійного розв’язання
- •Відомо також, що імовірність обману можна визначити як
- •1.13 Криптоаналіз rsa та дискретних логарифмiв методом -Поларда. Приклади розв’язку задач та задачі для самостійного розв’язання
- •Задача 1.
- •1.14 Криптоаналiз rsa методом квадратичного решета. Приклади розв’язку задач та задачі для самостійного розв’язання
- •Задача 1.
- •2.7 Аналіз методiв перетворень в перспективних симетричних криптографічних системах. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.7.1 Приклади розв’язку задач
- •2.8 Методи та засоби генерування та розподілу ключів. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.8.1 Приклади розв’язку задач
- •2.9 Симетричні потокові шифри. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.9.1 Приклади розв’язку задач
- •2.10 Стійкість асиметричних криптосистем, що базуються на криптоперетвореннях в простих полях. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.10.2 Приклади розв’язку задач
- •2.11 Стійкість асиметричних криптосистем, що базуються на криптоперетвореннях в групі точок еліптичних кривих. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.11.2 Приклади розв’язку задач
- •Використовуючи формули для додавання точок:
- •При подвоєнні маємо:
- •2.12 Електронні цифрові підписи та їх застосування. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.12.1 Приклади розв’язку задач
- •2.13 Криптографічні протоколи. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.14 Криптографічні протоколи направленого шифрування. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.14.1 Приклади розв’язку задач
- •Побудуйте однораундовий протокол автентифікації, використовуючи rsa криптографічне перетворення, оцініть стійкість протоколу, якщо довжина модуля
- •1) Факторизуємо модуль n і визначаємо прості числа p та q;
- •2.15 Криптографічні протоколи виробки та установки ключів. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.15.1 Приклади розв’язку задач
- •Для умов задачі 6 знайдіть закон розподілу загальних секретів.
- •Задача 10.
- •2.16 Криптографічні протоколи розподілу таємниці. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.16.2 Приклади розв’язку задач
- •2.16.3 Задачі для самостійного розв’язання
- •Задача 5.
- •2.17.1 Приклади розв’язку задач
- •2.17.2 Задачі для самостійного розв’язання
- •14. Оцініть імовірність нав’язування хибного повідомлення для випадку, коли для захисту використовується геш-функція гост-28147-89.
2.10 Стійкість асиметричних криптосистем, що базуються на криптоперетвореннях в простих полях. Приклади розв’язку задач та задачі для самостійного розв’язання
2.10.1 Основні теоретичні та практичні відомості
Криптографічні перетворення в простих полях Галуа історично вперше були застосовані для забезпечення передачі відкритих ключів (сертифікатів) по відкритих каналах зв’язку. На основі цього перетворення в подальшому було розроблено ряд протоколів-примітивів, що прийняті як національні стандарти, наприклад, стандарт ANSI X9.42. Крім того, ряд таких криптографічних примітивів використовуються для виробки ключів стандартів на цифрові підписи США - FIPS-186, Росії - ГОСТ Р 34.10-94 та України - ГОСТ 34.310-95.
Розглянемо два основних протоколи виробки загального секрету (ключів), коли в процесі виробки ключів відкриті ключі (сертифікати) передаються по відкритих каналах зв’язку.
Перший протокол базується на використанні при виробці загального секрету довгострокових ключів.
Нехай
в криптосистемі відомі загальносистемні
параметри
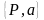 ,
де Р –
просте
число, а
– твірний елемент поля Галуа GF(P).
З кута зору вимоги найбільшої
складності криптоаналізу число Р
має бути “сильним”, наприклад, у
вузько-
му
значенні. Таке число можна подати у
вигляді
,
де Р –
просте
число, а
– твірний елемент поля Галуа GF(P).
З кута зору вимоги найбільшої
складності криптоаналізу число Р
має бути “сильним”, наприклад, у
вузько-
му
значенні. Таке число можна подати у
вигляді
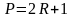 ,
(2.60)
,
(2.60)
де R – також просте число.
В ряді випадків до числа Р ставиться вимога, щоби в канонічному розкладі числа Р-1 містилось велике просте число, скажімо q, тоді
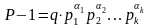 .
(2.61)
.
(2.61)
По суті, прості числа виду (2.60) та (2.61) дозволяють знайти (обчислити) також і твірний елемент а. Так в FIPS-186 та ГОСТ Р 34.10-94 прості числа мають вид (2.61).
В
цілому, загальносистемними параметрами
можуть бути або пара
,
або трійка цілих чисел
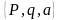 .
.
Для забезпечення цілісності та справжності параметрів та їх сертифікують математично (перевіряють, що P та q дійсно прості, а число а є твірним елементом) та логічно, коли кожний із загальносистемних параметрів підписується з використанням ключа сертифікації.
При відомих загальносистемних параметрах виробка загального секрету для А та В абонентів на основі довгострокових ключів здійснюється таким чином.
Кореспонденти
А та В виробляють особисті ключі
 та
та
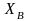 .
Потім кожен із них виробляє відкритий
ключ
.
Потім кожен із них виробляє відкритий
ключ
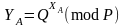 ,
(2.62)
,
(2.62)
і
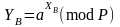 .
(2.63)
.
(2.63)
Відкриті ключі пересилаються між абонентами з забезпеченням їх ціліснос- ті та справжності, наприклад, через центр сертифікації або з використанням ланцюга сертифікатів. Далі кожен із абонентів обчислює загальний секрет як
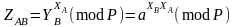 ,
(2.64)
,
(2.64)
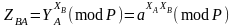 .
(2.65)
.
(2.65)
Можна легко перевірити, що
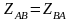 (2.66)
(2.66)
і у обох абонентів є один і той же загальний секрет. Використовуючи одну і ту ж функцію kdf виробки ключа, кожен із абонентів може виробити одинаковий ключ, наприклад,
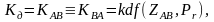 (2.67)
(2.67)
де
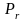 –
є параметр виробки ключа. В найпростішому
випадку значенням
може бути номер сеансу.
–
є параметр виробки ключа. В найпростішому
випадку значенням
може бути номер сеансу.
Більш
високу криптографічну стійкість та
криптографічну живучість забезпечує
протокол виробки ключів на основі
довгострокових та сеансових ключів.
У цьому випадку спочатку згідно з (2.62)
- (2.67) виробляються відкриті довгострокові
ключі
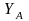 та
та
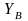 ,
що розсилаються з забезпеченням їх
цілісності та справжності.
,
що розсилаються з забезпеченням їх
цілісності та справжності.
Сеансові
ключі формуються при кожному сеансі
зв’язку. Спочатку формуються особисті
сеансові ключі
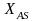 та
та
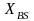 ,
потім відкриті сеансові ключі
,
потім відкриті сеансові ключі
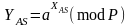 ,
(2.68)
,
(2.68)
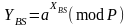 .
(2.69)
.
(2.69)
Відкриті сеансові ключі пересилаються перед кожним сеансом або поміщаються в першому блоці, що пересилається.
Спочатку обчислюється сеансовий загальний секрет
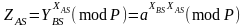 ,
(2.70)
,
(2.70)
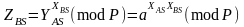 .
(2.71)
.
(2.71)
Із
(2.70) та (2.71) видно, що
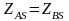 ,
тому кожен із абонентів може виробити
однаковий секретний сеансовий ключ
,
тому кожен із абонентів може виробити
однаковий секретний сеансовий ключ
 .
(2.72)
.
(2.72)
В
подальшому, використовуючи довгостроковий
ключ
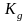 та сеансовий
та сеансовий
 ,
можна здійснити конфіденційний зв’язок.
,
можна здійснити конфіденційний зв’язок.
Більш переважним є формування сеансового ключа відповідно до правила
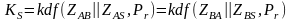 ,
(2.73)
,
(2.73)
де
символ || є знаком конкатенації значень,
наприклад,
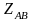 та
та
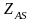 .
.
Аналіз
показує [26], що найбільшу загрозливість
для криптоперетворень в простих полях
складають атаки типу універсальне
розкриття та повне розкриття. Сутність
атаки типу універсальне розкриття
заключається в знаходженні деякого
математичного алгоритму, що дозволяє,
в загальному випадку, обчислити
та
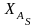 і
та
.
До сьогодні такі випадки не відомі.
і
та
.
До сьогодні такі випадки не відомі.
Сутність атаки типу повне розкриття заключається в розв’язку дискретних логарифмічних рівнянь
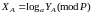 ,
(2.74)
,
(2.74)
та
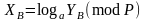 .
.
При розв’язку (2.74) вважається, що загальносистемні параметри (Р, а) та відкриті ключі та є відомими.
Якщо
криптоаналітик визначить особистий
ключ
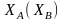 ,
то в подальшому він зможе нав’язувати
хибні загальні секрети та відповідно
хибні пові-домлення. Для суттєвого
ускладнення можливості нав’язування
хибних загальних секретів використовують
як довгострокові, так і сеансові загальні
секрети. Тобто на кожний сеанс ключ
формують за правилом (2.73). В цьому випадку
для порушення конфіденційності необхідно
розв’язувати вже два дискретних
логарифмічних рівняння, наприклад,
(2.62) та (2.68) або (2.63) та (2.69). При удачі
криптоаналітик може визначити три
особистих ключі
,
то в подальшому він зможе нав’язувати
хибні загальні секрети та відповідно
хибні пові-домлення. Для суттєвого
ускладнення можливості нав’язування
хибних загальних секретів використовують
як довгострокові, так і сеансові загальні
секрети. Тобто на кожний сеанс ключ
формують за правилом (2.73). В цьому випадку
для порушення конфіденційності необхідно
розв’язувати вже два дискретних
логарифмічних рівняння, наприклад,
(2.62) та (2.68) або (2.63) та (2.69). При удачі
криптоаналітик може визначити три
особистих ключі
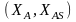 або
або
 .
.
Розглянемо основні алгоритми та складність розв’язку дискретних логарифмічних рівнянь. На сьогодні відомо декілька алгоритмів і відповідно методик складності розв’язку дискретних логарифмічних рівнянь. Основними із них є алгоритм -Полларда, Поліга-Хелмана [11], загального решета числового поля [10,11] та алгоритм Купершмідта [11].
Історично першим з’явився метод і на його основі алгоритм -Полларда. Нехай необхідно розв’язати дискретне логарифмічне рівняння
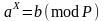 . (2.75)
. (2.75)
Формуватимемо
випадкові пари цілих чисел
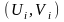 та
та
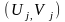 .
Нехай знайдено такі дві пари чисел
та
,
що
.
Нехай знайдено такі дві пари чисел
та
,
що
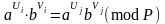 . (2.76)
. (2.76)
Підставимо (2.75) в (2.76), в результаті маємо
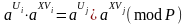
або
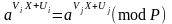 .
(2.77)
.
(2.77)
В рівнянні (2.77) згідно з теоремою Ойлера ступені можна прирівняти за модулем (Р-1), тобто
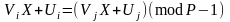 .
(2.78)
.
(2.78)
Із (2.78) в свою чергу маємо
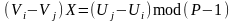
або
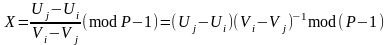 .
(2.79)
.
(2.79)
Таким
чином, необхідно знайти пари цілих чисел
та
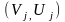 ,
що задовольняють (2.76), а далі підставивши
їх в (2.79), отримаємо розв’язок. По суті
алгоритм
-Полларда
і забезпечує формування цих пар чисел.
,
що задовольняють (2.76), а далі підставивши
їх в (2.79), отримаємо розв’язок. По суті
алгоритм
-Полларда
і забезпечує формування цих пар чисел.
Виберемо
як перший елемент послідовності
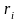 як
як
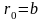 .
(2.80)
.
(2.80)
Далі обчислюватимемо послідовність за рекурентним правилом
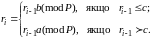 (2.81)
(2.81)
Постійну с вибирають таким чином, щоби с знаходилось між а та b приблизно на однаковій відстані. Але в більшості випадків його підбирають.
Послідовність
називають послідовністю
-Полларда.
Для успішного розв’язку дискретного
логарифмічного рівняння необхідно
знайти два значення
та
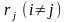 таких, що
таких, що
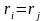 .
(2.82)
.
(2.82)
Після цього знаходять значення та та обчислюють згідно з (2.79) особистий ключ.
Метод Поліга-Хемана базується на китайській теоремі про лишки [17]. Нехай знову необхідно розв’язати рівняння
. (2.83)
Розв’язок виконується в декілька етапів:
знаходиться канонічний розклад числа Р-1;
обчислюються лишки за модулями канонічного розкладу;
обчислюється значення Х згідно з китайською теоремою про лишки.
Перший етап виконується достатньо просто, так як згідно з (2.60) та (2.61) на етапі побудови пари розклад числа Р-1 є відомим. Інакше довести, що а – твірний елемент, дуже складно. Тому на першому етапі Р-1 подається у вигляді:
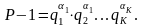 (2.84)
(2.84)
Далі
знайдемо лишки
від ділення Х на
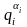 ,
в результаті для кожного
,
в результаті для кожного
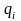 отримаємо
отримаємо
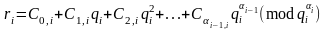 , (2.85)
, (2.85)
причому
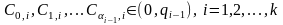 .
.
Необхідно
знайти коефіцієнти
 для усіх i.
Оскільки лишки подано за модулем
,
то
для усіх i.
Оскільки лишки подано за модулем
,
то
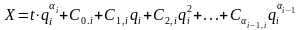 . (2.86)
. (2.86)
Запишемо далі (2.83) у вигляді
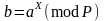 .
(2.87)
.
(2.87)
та
піднесемо ліву і праві частини (2.87) до
ступеня
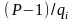 .
В результаті отримаємо
.
В результаті отримаємо
 .
2.88)
.
2.88)
Обчислимо
значення ,
підставивши в нього (2.86), в результаті
маємо
,
підставивши в нього (2.86), в результаті
маємо
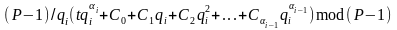 .
(2.89)
.
(2.89)
Якщо перемножити на вираз в дужках, то ми отримаємо
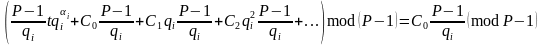 .
(2.90)
.
(2.90)
В
цьому можна переконатися, так як всі
члени, крім
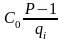 діляться на Р-1,
тому
вони даватимуть лишок рівний 0. З
урахуванням (2.90) (2.10.88) має вигляд
діляться на Р-1,
тому
вони даватимуть лишок рівний 0. З
урахуванням (2.90) (2.10.88) має вигляд
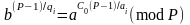 .
(2.91)
.
(2.91)
Тепер
піднесемо ліву та праві частини (2.87) до
ступеня
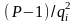 ,
в результаті отримаємо
,
в результаті отримаємо
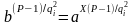 .
(2.92)
.
(2.92)
Підставивши в (2.92) вираз (2.86), отримаємо
 .
(2.93)
.
(2.93)
Оскільки на (Р-1) тепер не ділитимуться два члени
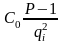 та
та
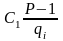 ,
,
тому вони не дорівнюватимуть нулю.
Аналогічно
можна перетворити (2.87) для усіх
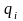 і для усіх ступенів. В результаті для
конкретного
модуля ступеня отримаємо
і для усіх ступенів. В результаті для
конкретного
модуля ступеня отримаємо
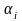 порівнянь
порівнянь
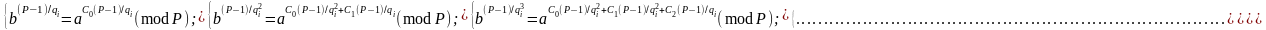 (2.94)
(2.94)
Використовуючи
(2.94), можна знайти усі лишки виду (2.84),
для цього достатньо знайти коефіцієнти
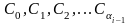 .
Їх ми знаходимо, використовуючи (2.94).
Спочатку, перебираючи значення
.
Їх ми знаходимо, використовуючи (2.94).
Спочатку, перебираючи значення
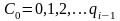 ,
знаходимо
і так далі для усіх ступенів, включно
до
,
знаходимо
і так далі для усіх ступенів, включно
до
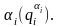
Таким чином, для фіксованого система (2.94) дозволяє визначити коефіцієнти і, як наслідок, лишок (2.85). Для знаходження другого лишку необхідно взяти наступне значення .
Таким чином, ми одержуємо лишки
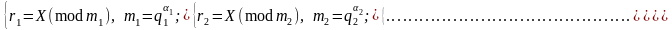 (2.95)
(2.95)
Використовуючи китайську теорему про лишки, отримаємо [17]
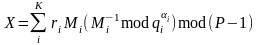 ,
(2.96)
,
(2.96)
де
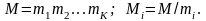
Зворотний
елемент
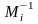 знаходимо із порівняння
знаходимо із порівняння
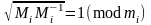 .
.
Таким чином, (2.96) дає розв’язок дискретного логарифмічного порівняння виду (2.83) або (2.87).
Важливими в теоретичному плані є задачі оцінки складності розв’язку дискретних логарифмічних рівнянь. Для алгоритму -Полларда як асимптотич-ну оцінку складності розв’язку можна використовувати співвідношення
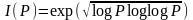 .
(2.97)
.
(2.97)
Інші алгоритми мають субекспоненціальну складність виду
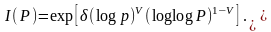 (2.98)
(2.98)
Так,
при застосуванні загального решета
числового поля
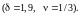 Є відомості, що алгоритм Купершмідта
дозволяє розв’язати дискретне
логарифмічне рівняння в полі GF(2n)
зі складністю
Є відомості, що алгоритм Купершмідта
дозволяє розв’язати дискретне
логарифмічне рівняння в полі GF(2n)
зі складністю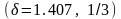 .
.
Складність алгоритму Поліга-Хелмана можна оцінити безпосередньо за наведеним вище алгоритмом.
