
Шпоры по лин. ал
.docx|
1. Понятие ранга матрицы. Теорема о базисном миноре. Определение: ранг матрицы это наивысший из порядков миноров этой матрицы, отличных от нуля. Определение: минором порядка k матрицы А называется определитель матрицы k-ого порядка, элементы которого стоят на пересечении выбранных k-строк и k-столбцов, т.е.
Замечание: если в матрице А все миноры k-ого порядка равны нулю, то все миноры более высокого порядка тоже равны нулю. Определение: минором порядка n матрицы А называется базисным, если он отличен от нуля, а все миноры более высокого порядка равны нулю. Определение: рангом матрицы А называется порядок её базисного минора, т.е. ранг матрицы равен n, если в матрице существует ненулевой минор n-ого порядка, а все миноры более высокого порядка равны нулю Rang A= rg A. Теорема о базисном миноре: для любой матрицы А базисные столбцы линейно независимы и любой столбец являющийся линейной комбинаций базисных столбцов. Следствие: если RgA<n, то столбцы линейно зависимы. Следствие: А – квадратичная матрица detA=0 тогда и только тогда, когда столбцы матрицы А линейно зависимы.
|
2. Понятие ранга матрицы. Теорема о ранге матрицы. Определение: минором порядка n матрицы А называется базисным, если он отличен от нуля, а все миноры более высокого порядка равны нулю. Определение: рангом матрицы A (rang A) называется максимальный порядок минора (базисного минора), отличного от нуля. (Если А – нулевая матрица, т.е. все aij=0, то rang A=0). Чаще всего ранг обозначается числом r. Теорема: ранг матрицы равен максимальному числу линейно независимых столбцов этой матрицы. Следствие: для любой матрицы А максимальное число линейно независимых столбцов равно числу линейно независимых строк. |
|
3. Элементарные преобразования матриц. Инвариантность ранга матрицы при элементарных преобразованиях. Вычисление ранга матрицы. Определение: элементарные преобразования матрицы не изменяют её ранга. Определение: элементарными преобразованиями матрицы называются следующие преобразование: а) перестановка строк б) умножение на число отличное от нуля в) прибавление к одной строке другую умноженную на число г) аналогичные преобразование для столбцов Замечание: эти преобразование обратимы А->B, то B->A Определение: говорят, что матрица имеет ступенчатый вид если: 1)ниже нулевой строки нулевые строки 2)если ai1=…=aik-1=0, aik≠0, то аik=1 и S>I и t≤k: ast=0 Замечание: ранг ступенчатой матрицы равен числу ненулевых строк. Теорема: всякую матрицу конечным числом элементарных преобразований строк можно привести к ступенчатому виду.
|
4.Критерий совместности систем линейных алгебраических уравнений (теорема Кронекера - Капелли). Теорема Кронекера – Капелли: Система ЛАУ совместна тогда и только тогда, когда ранг матрицы системы равен расширенной матрице системы, т.е. rgA=rgА’ A’=(A|B); A*B=X; Определение: две системы с переменными x1;...;xn называются эквивалентными, если они обе несовместны либо все решения одной являются решениями другой и наоборот. Определение: частным решением системы называется упорядоченный набор чисел а1,…,аn, обращающий в тождество каждое из уравнений системы. Определение: система ЛАУ называется совместной, если она имеет хотя бы одно частное решение и несовместной, если нет решений. Определение: общим решением совместной системы называется множество всех частных решений. Определение: Совместной называется система, у которой существует хотя бы одно частное решение. Определение: эквивалентными называются системы, имеющие одно и то же общее решение или несовместные. |
|
5.Метод Гаусса решения систем линейных алгебраических уравнений. Определение: общий вид система из m линейных уравнений с n неизвестных x1,…,xn:
Лемма: элементарному преобразованию строк A’ соответствует эквивалентной системе уравнений. Теорема: метод Гаусса заключается в переходе от системы к эквивалентной системе, основная матрица которой имеет ступенчатый вид: A’= Переход совершается с помощью элементарных преобразований расширенной матрицы только с её строками |
6.Однородные системы линейных алгебраических уравнений. Свойства решений. Критерий наличия ненулевых решений. Теорема: однородная система ЛАУ имеет ненулевое решение тогда и только тогда, когда ранг матрицы системы меньше числа неизвестных. Теорема: если x(1) и x(2) – решения системы (2), то для любых чисел α и β, линейная комбинация αx(1) + βx(2) – решение системы. Замечание: теорема справедлива, если x(1), …, x(x)- решения системы, α1,…, αk – числа, т.е. α1x(1) +…+ αkx(k) – решение системы
Определение: однородной называется система A*X=0, то есть система, в которой B=0. |
|
7.Фундаментальная система решений однородной системы уравнений. Теорема о существовании фундаментальной системы решений. Если RgA=n, то система ЛАУ имеет только нулевое решение. Пусть
r=RgA<n.
Тогда в матрице А существует базисный
минор порядка r.
Не ограничивая общности считаем, что
M Строки
Назовём неизвестные x1,x2,xr- главными неизвестными, а неизвестные xr+1,…,xn-свободными неизвестными.
Системы
(1) и (2) равносильны, т.к. Δ=M Теорема: если ранг матрицы А меньше числа неизвестных, то система однородных ЛАУ имеет n-r линейно независимых решений. Определение: Ф.С.Р. однородной системы уравнений называется любая система из n-r линейно независимых решений. |
8.Линейная зависимость любых n - r + 1 решений однородной системы (n - число неизвестных, r - ранг матрицы системы). Общее решение однородной системы линейных алгебраических уравнений. Теорема: если r=rgA<n, то любая система из (n-r+1) решений системы линейно зависима. Теорема: если r=rgA<n и x(1),…,x(n-r)- Ф.С.Р. однородной системы ЛАУ, то общее решение системы имеет вид: x=C1(x(1))+C2(x(2))+…+Cn-r(x(n-r)), где C1,…,Cn-r – произвольные числа. Определение: система(1) называется приведённой для системы (2), если их основные матрицы совпадают. A*X=B (1); A*X=θ (2) |
|
9.Общее решение совместной неоднородной системы линейных алгебраических уравнений. Определение: система(1) называется приведённой однородной системой ЛАУ для неоднородной системы(2) n-число неизвестных r≤n. A*X=B(1) A*X=θ(2); A’=(A|B); Теорема: общее решение совместной неоднородной системы ЛАУ представляется как сумма некоторого частного решения этой системы и общего решения приведённой системы. Определение:
общее
решение неоднородной системы равно
сумме какого-либо её частного решения
и общего решения приведённой однородной
системы:
Xобщ.неодн.=Xчастн.неодн.+X0обще.=Xч.н.+с1 Определение: частное решения неоднородной системы можно найти, положив свободные переменные, например, равными нулю. Теорема: если rgA=rgA’=r, причём r<n и x(1),…,x(n-r)-Ф.С.Р. приведённой системы, Xч.н.-частное решение, то общее решение Xо.н.=Xч.н.+С1X(1)+…+Cn-rX(n-r), где С1,…,Сn-r-произвольные числа Выводы: 1)RgA≠RgA’, то система несовместна. 2)RgA=RgA’=r, то система совместна. а)RgA=r=n-система имеет единственное решение. б)RgA=r<n-система имеет бесконечно много решений. |
10.1.Определение линейного ( векторного) пространства, действительного и комплексного. Простейшие свойства. Примеры линейных пространств. Определение: не пустое множество V элементов произвольной природы называется действительным(комплексным) линейным пространством если: а)x и y є V поставлен в соответствие элемент zєV, которой называется суммой этих элементов x и y и обозначается z=x+y б)любому элементу xєV и любому действительному(комплексному) числу λ поставлен в соответствии элемент λxєV которой называют произведением элемента x на число λ. При
этом выполняются аксиомы:
1) 8)1* 1)Единственность нулевого элемента: допустим существует θ1 и θ2єV: θ1=θ2+θ2=θ2+θ1=θ2 2)Единственность противоположного элемента: Пусть xєV и x’ и x”єV:x+x’=θ и x+x”=θ; x’=x’+θ=x’+(x+x”)=(x’+x)+x”=(x+x’)+x”=θ+x”=x” 3)Для любого xєV:0*x=θ;0*x=0*x+θ=0*x+(x+x’)=(0*x+x)+x’=(0*x+1*x)+x’=(0+1)x+x’=1*x+x’=x+x’=θ 4)xєV(-x)=(-1)x; x+(-1)x=1*x+(-1)*x=(1+(-1))x=0*x=θ 5)α:α*θ=θ; α*θ=α(0*θ)=(α*0)*θ=0*θ=θ 6)α:α(-x)=(-αx) 7)αx=θ либо α=0,либо x=0 |
|
10.2.Определение линейного ( векторного) пространства, действительного и комплексного. Простейшие свойства. Примеры линейных пространств. Примеры: 1)Vi-множество векторов на прямой, плоскости, в пространстве i=1,2,3 2)[a;b]-отрезок f(x)-определена и непрерывна на [a;b]; C[a;b]-множество всех функций непрерывна на [a;b] 3)Множество всех действительны(комплексных) чисел R(C) относительно обычных операций – действительных(комплексных) линейное пространство 4)n-мерное действительное(комплексное) координатное пространство (Rn,Cn) 5)m,nєN, Am*n=||aij||m*n; m*n – множество всех матриц действительных(комплексных) размеров m*n 6)Pn[x]-множество всех множеств от переменной x степени ≤ n; P(x)=α0+α1x+…+αnxn; α0,α1,…,αnєR;
|
11.Линейно зависимые и линейно независимые системы векторов. Критерий линейной зависимости, достаточные условия линейной зависимости. Определение: система элементов x1,x2,…,xm линейного пространства V называется линейно зависимой, если числа λ1,λ2,…,λm не все равные 0 (|λ1|+…+|λm|≠0) такие, что λ1x1+λ2x2+…+λmxm=θ (1) Система элементов x1,x2,…,xmєV называется линейно независимой если из равенства (1) следует, что λ1=λ2=…=λm=0 Определение: элемент xєV называется линейной комбинацией элементов x1,x2,…,xmєV, если числа α1,…,αn такие, что x=α1x1+…+αmxm. Теорема: система векторов x1…xnєV линейно зависима тогда и только тогда, когда хотя бы один вектор системы линейно выражается через остальные. Теорема: если система векторов x1,…,xm-1,xm-линейно зависима, а её подсистема x1,…,xm-1 тоже линейно зависима, то xm-линейно выражается через x1,…,xm-1
|
|
12.Базис линейного пространства. Координаты вектора в данном базисе, координаты суммы векторов и произведения вектора на число. Необходимое и достаточное условие линейной зависимости системы векторов. Определение: упорядоченная система элементов е1,…,еn линейного пространства V называется базисом этого пространства, если: 1)е1,…,еn- линейно независима 2)xєV α1,…,αn такие, что x=α1e1+…+αnen При
этом представление x= Теорема: если задан базис в линейном пространстве V, то xєV столбец координат x в е1…еn определяется однозначно. Теорема: при сложении x и y столбцы их координат в базисе е1…еn-складываются, при умножении элемента x на произведение число λ столбец координат x умножается на λ. Лемма: пусть е1…еn-базис V. Система векторов f1,…,fkєV является линейно зависимой тогда и только тогда, когда линейно зависимы столбцы координат этих элементов в е1…еn |
13.Размерность линейного пространства. Теорема о связи размерности и базиса. Определение: линейное пространство V называется n-мерным пространством, если в V n независимых элементов, а система из любых n+1 элементов V линейно зависима. В этом случае n называется размерностью линейного пространства V и обозначается dimV=n. Линейное пространство V называется бесконечномерным, если NєN в пространстве V система(линейно независимая), содержащая N элементов. Теорема: 1)Если V-n-мерное линейное пространство, то любая упорядоченная система из n линейно независимых элементов этого пространства образует базис. 2)Если в линейном пространстве V базис, состоящий из n элементов, то размерность V равна n(т.е. dimV=n) |
|
14.1.Матрица перехода от одного базиса линейного пространства к другому. Преобразование координат вектора при изменении базиса. Берём
произвольный элемент xєV
и раскладываем по базисам [e]
и [
Определение:
матрицей
перехода от базиса [e]
к базису [
T= |
14.2.Матрица перехода от одного базиса линейного пространства к другому. Преобразование координат вектора при изменении базиса. Теорема: если V-n-мерное пространство, то невырожденные квадратные матрицы порядка n и только они могут служить матрицами перехода от одного базиса к другому. Следствие:
если
Т –матрица перехода от базиса [e]
к базису [ |
|
15.Определение линейного подпространства. Свойства линейного подпространства. Примеры. V-линейное пространство (R/C) Определение: непустое подмножество L линейного пространства V называется линейным подпространством линейного пространства V, если выполняются следующие условия: 1)x,yєL: x+yєL 2)xєL λ:λxєL Из определения следует, что x1,..,xkєL и λ1,…,λkєR(C) λ1x1+…+λkxkєL Свойства: 1)Линейное подпространство L линейного пространства V само является линейным пространством относительно операции сложения и умножения на число, определённые в V. 2)Любое линейное подпространство n-мерного пространства конечномерна и его размерность не превосходит n. Если dimV=n, LV(L-линейное подпространство), то dimL≤n. 3)Линейное подпространство L конечномерного пространства V совпадает со всем пространством тогда и только тогда, когда dimL=dimV Примеры: 1)V-произвольное линейное пространство {θ}-содержат только θ {θ}-нулевое подпространство пространства V. L=V-подпространство V. 2)V-линейное пространство геометрических векторов. а)Зафиксируем π(плоскость) L1-множество всех векторов ||π L1={xєV:x||e} б)Зафиксируем прямую l L2-множество всех векторов || l L2={xєV:x||l} 3)Ax=θ; A=||aij|m*n; Ln*s |
16. Определение линейной оболочки системы векторов. Теорема о размерности линейной оболочки. Определение:
пусть
x1,…,xn-элементы
линейного пространства V,
а λ1,…,λn-числа,
рассмотрим линейную комбинацию вида
Множество всех линейных комбинаций называется линейной оболочкой системы элементов x1,…,xk. Обозначают L{x1,…,xm}={λ1x1+…+λmxm} Теорема(о размерности линейной оболочки): пусть x1,…,xm-элементы линейного пространства V dimL{x1…xm} линейной оболочкой элементов x1,…,xm равна максимальному числу линейно независимых элементов в система x1,…,xm. Теорема: пусть x1,…,xn-элементы линейного пространства V. Линейная оболочка L{x1…xm} является наименьшим линейным подпространством V, содержащим элементы x1…xm
|
|
17.Сумма и пересечение подпространств. Прямая сумма подпространств. Теорема о разложении линейного пространства в прямую сумму подпространств. V-линейное пространство; V1 и V2-линейные подпространства пространства V. Определение: пересечением(V1∩V2) линейных подпространств V1 и V2 называется множество всех элементов, которое є этим подпространствам одновременно. V1∩V2={xєV,xєV1,xєV2} Суммой V1+V2 линейных подпространств V1 и V2 называется множество всех элементов пространства V вида x=x1+x2 где x1єV1, x2єV2; V1+V2={xєV,x=x1+x2; x1єV1; x2єV2} Теорема: сумма и пересечение линейных подпространств являются сами подпространствами. Определение:
сумма V1+V2
называется прямой суммой, если
V1∩V2={θ}.
Обозначение V1 Теореме:
каждый
элемент xєV1 Теорема:
линейное
пространство V
является прямой суммой подпространств
V1
и V2
(т.е. V=V1 1)dimV=dimV1+dimV2 2) V1∩V2={θ}
|
18.1.Определение линейного оператора. Простейшие свойства. Примеры. Действия с линейными операторами и их свойства. Определение: оператором линейного пространства V называется закон, по которому каждому элемента пространства V ставится в соответствие единственный элемент того же самого пространства. А,Р,D,У – обозначение оператора V. Путь А-оператор пространства V. xєV обозначим Ax-результат действия A на элемент x А:V->V; Если y=Ax; где yєV, то y называется образом элемента xєV, а x-прообразом элемента yєV. Определение: оператор А линейного пространства V называется линейным оператором, если для x,yєV и произвольного числа λ выполняются: 1)A(x+y)=Ax+Ay 2)A(λx)=λAx. Свойства: 1)Линейный оператор отображает нулевой элемент на нулевой элемент, т.е. Aθ=θ 2)xєV:A(-x)=-Ax 3)Оператор А линейного пространства V является линейным оператором тогда и только тогда, когда x1,…,xkєV и λ1,…,λk выполняется: A(λ1x1+…+λkxk)=λ1Ax1+…+λkAxk 4)если x1,…,xkєV линейно зависимы, а А- линейный оператор V, то образы Ax1,Ax2,…,Axk-также линейно зависимые. A(λ1x1+…+λkxk)=λAx1+…+λkAxk=Aθ=θ => Ax1,…,Axk-линейно зависимые. |
|
18.2.Определение линейного оператора. Простейшие свойства. Примеры. Действия с линейными операторами и их свойства. Определение: 1)пусть А и В – операторы линейного пространства V. Операторы А и В называются равными (А=В), если xєV: Ax=Bx 2)оператор У называется тождественным или единичным, если xєV: Уx=x 3)оператор O называется нулевым, если xєV Ox=θ У,О- линейные операторы V. Теорема: множество всех линейных операторов L(V) линейного пространства V само является линейным пространством. Определение: произведением операторов А и В линейного пространства V называется оператором АВ, действующему по правилу xєV:(AB)x=A(βx). Теорема: если А и B линейные операторы V А,ВєL(V), то AB тоже линейный оператор V АВєL(V) Свойства произведения оператора: A,B,CєL(V), λ-число 1)λ(AB)=(λA)B=A(λB) 2)(A+B)C=AC+BC 3)(AB)C=A(BC) 4)AУ=УА=А 5)Aθ=θA=θ 6)A(B+C)=AB+AC |
19.Матрица оператора в базисе. Примеры. Нахождение координат образа по координатам прообраза. [e]=(e1,…,en)-базис Vn Лемма: линейный оператор А однозначно определён образами Ae1,…,Aen базисных элементов е1…еn. Определение: матрицей Ае линейного оператора А в базисе [e] называется квадратная матрица порядка n в j-ом столбце которой стоят координаты вектора Aej в базисе [e]. Лемма: n векторов y1,…,ynєVn единственный линейный оператор B такой, что Be1=y1…Ben=yn. Нахождение координат образа: [e]:A->Ae;
x= Лемма: если АєL(Vn), [e]=(e1,…,en)-базис, С=||clt||nk-матрица размеров n*k, то A((e1,…,en)C)=(Ae1,…,Aen)C=(e1,…,en)(AeC) |
|
20.Теорема о взаимно однозначном соответствии в фиксированном базисе n - мерного линейного пространства между линейными операторами и квадратными матрицами порядка n. Теорема: пусть [e]=(e1,…,en)-некоторый базис пространства Vn и квадратная матрица порядка n. Тогда существует единственный линейный оператор ВєL(Vn) такой, что матрица В является матрицей оператора В в базисе [e] (т.е. B=Be). Замечание: С=||cij||nk; B=||bij||nk. Если (e1,…,en)B=(e1,…,en)C, то B=C. Вывод: в фиксированном базисе [e] линейного пространства Vn взаимоодназначное соответствие между линейными операторами AєL(Vn) и квадратными матрицами AeєLm*n [e]:A<->Ae. Ae-матрица А в [e]. |
21.Матрица суммы операторов, произведения оператора на число и произведения операторов. Пусть Vn-n-мерное пространство, A,BєL(Vn); λ-число; [e]=(e1,…,en)-базис Vn; Ae,Be-матрицы операторов A,B в[e]. Теорема: если А и В – линейные операторы єL(Vn) и λ-число, то 1)(А+В)е=Ае+Ве, где (А+В)е- матрица операторов А+В в [e]; 2)(λA)e=λAe, где (λA)e- матрица операторов λA в [e]; 3)(AB)e=AeBe, где (AB)e – матрица операторов AB в [e].
|
|
22.Обратный оператор для данного линейного оператора и его свойства. Критерий обратимости линейного оператора. Матрица обратного оператора. Примеры обратимых и необратимых операторов. Определение: линейный оператор пространства V называется обратимым, если существует такой оператор В пространства V, что AB=BA=У.(У- тождественный оператор). Оператор В называется обратным к оператору А и обозначается B=A-1. Свойства: 1)если А-1 существует, то он линейный. 2)единственность обратного оператора. 3)если А обратим, то ядро этого оператора kerA={θ} 4)если А- обратимый оператор, то образ УmA=V. Теорема(критерий линейного оператора в конечномерном пространстве Vn): пусть АєL(Vn); оператор А обратим в том и только в том случае, когда он невырожденный (т.е. тогда и только тогда, когда detA≠0). |
23.Преобразование матрицы линейного оператора при изменении базиса. Подобные матрицы. [e]=(e1,…,en)-базис
I;
[ A( A( A Определение: квадратные матрицы B и D порядка n называются подобными, если D=Q-1BQ, где Q-некоторая невырожденная матрица порядка n. Следствия: 1)Подобные матрицы и только они задают один и тот же оператор в различных базисах. 2)Определитель матрицы линейного оператора не зависит от выбора базиса.
|
|
24.Характеристический многочлен матрицы. Характеристический многочлен линейного оператора, его инвариантность. А=||aij||nn; E=En; λ-произвольная переменная; Матрица А-λЕ называется характеристической матрицей матрицы А. Рассмотрим
многочлен det(A-λE)=|A-λE|= Определение: многочлен det(A-λE) – называется характеристическим многочленом матрицы А. Степень характеристического многочлена равна n коэффициенту при λn=(-1)n. Теорема: характеристические многочлены подобных матриц совпадают. Определение: характеристический многочлен оператора А называется характеристическим многочленом матрицы этого оператора в некотором базисе V. Следствие: характеристический многочлен линейного оператора А n-мерного пространства Vn на зависит от выбора базиса. |
25.Собственные значения и собственные векторы линейного оператора. Примеры. Теорема о собственных значениях линейного оператора в конечномерном пространстве. Нахождение собственных значений и координат собственных векторов. V-линейное пространство(R или С); A-линейный оператор V, AєL(V); Определение: действительное(комплексное) число λ называется собственным значением линейного оператора А, если в пространстве V существует ненулевой вектор x такой, что Ax=λx; x≠θ; Любой вектор x≠θ называется собственным вектором оператора А, соответствующий собственному значению λ. Теорема: В действительном линейном пространстве Vn действительные корни характеристического многочлена оператора А и только они являются собственными значениями оператора А. В комплексном линейном пространстве Vn все корни характеристического многочлена оператора А и только они являются собственными значениями оператора А. |
|
26.Свойства собственных векторов, отвечающих одному и тому же собственному значению линейного оператора. Теорема о линейной независимости собственных векторов, отвечающих попарно различным собственным значениям. Пусть V-линейное пространство V’ V. Определение. Линейное подпространство V’ V называется инвариантным относительно A, если x V: Ax V. Теорема. Все собственные векторы линейного оператора A, соответствующие собственному значению λ0 вместе с θ образуют линейное подпространство V’, инвариантное относительно A. Док-во: V’={x V: Ax = λ0x} 1) V’ – линейное подпространство x1, x2 V’ A(x1, x2 ) = Ax1 + Ax2 = λ0x1 + λ0x2 = λ0( x1 + x2 ) => x1 + x2 V’ A( μx1 ) = μAx1 = μλ0x1 = λ0( μx1 ) => μx1 V’. Докажем инвариантность V’ относительно A x V’: т.к. V’ – линейное подпространство, следовательно V’ инвариантно относительно A. Теорема 10. Если λ1, λ2, …, λk – различные собственные значения оператора A (т. е. λi ≠ λj, при i ≠ j, то собственные вектора f1, f2, … , fk, отвечающие данным собственным значениям являются линейно независимыми.). |
27.Критерий диагональности матрицы линейного оператора. Теорема о приведении к диагональному виду матрицы линейного оператора с простыми собственными значениями. Определение 15. Квадратная матрица Anxn имеет диагональный вид, если i, j = 1, …, n: i ≠ j, aij = 0 ( aij = 0 ), т.
е. А =
Теорема 11. ( Критерий диагональности матрицы линейного оператора ). Пусть Vn – n-мерное линейное пространство, A L( Vn ), [e] = ( e1, … , en ) – базис Vn, Ae – матрица оператора А в [e]. Матрица Ae линейного оператора в базисе [e] диагональна т. и т. т., когда базис состоит из собственных векторов оператора A, причём в этом случае Aei = λiei i=1, …, n ( т.е. λi собственное значение соответствующее собственному вектору ei. Оператор называется диагонализируемым, если в пространстве Vn базис, в котором матрица оператора диагональна. Оператор диагонализируем в пространстве т. и т. т., когда в базисе базис из собственных векторов этого пространства. Ae – диагональная матрица. Теорема 12. Пусть A L( Vn ). Если у оператора n различных собственных значений ( λ1, λ2, …, λn ), то A – диагонализируемый оператор ( т. е. в Vn базис, в котором матрица оператора имеет диагональный вид ). Определение 16. Говорят, что квадратная матрица A приводится к диагональному виду, если она подобна диагональной матрице, т. е. если Tnxn ( det T ≠ 0 ) такая, что A~ = T-1AT, где Следствие: Если матрица A имеет n различных корней, характеристического многочлена, то её можно привести к диагональному виду. |
|
28.Билинейные формы в действительном линейном пространстве. Симметричные и кососимметричные билинейные формы, представление билинейной формы через координаты векторов. V – действительное линейное пространство. Определение: Билинейной формой на линейном пространстве называется числовая функция F( x, y ) от 2-х элементов x, y V, линейная по каждому аргументу ( при фиксированном втором ). Т. е. x, y, z V и (действительного). 1) F( x + z, y ) = F( x, y ) + F( z, y ); F( x, y ) = F( x, y ); 2) F( x, y + z ) = F( x, y ) + F( x, z ); F( x, y ) = F( x, y ). Примеры: 1) f и q – линейные формы на V. F( x, y ) = f( x )g( y ) – билинейная форма. 2) V3 – линейное пространство геометрических векторов x, y V3. F( x, y ) = ( x, y ) = |x|*|y|*cos - билинейная форма. Определение: Билинейная форма F( x, y ) на V называется: 1) Симметричной, если x, y V F( x, y ) = F( y, x ) 2) Кососимметричной, если x, y V F( x, y ) = -F( y, x ). F( x, y ) – билинейная форма на n-мерном линейном пространстве Vn [e] = ( e1, e2, …, en ) – базис Vn x, y Vn x = ni = 1 iei = ( e1, …, en )( 1…n ) = ( e1, … , en ) y = nj = 1 jej = ( e1, …, en )( 1…n ) = ( e1, … , en ) = ( 1…n ) и = ( 1…n ); ( 1…n ) и ( 1…n ) – столбцы! |
29.Преобразование матрицы билинейной формы при изменении базиса. Vn – n-мерное пространство; F( x, y ) – билинейная форма на Vn. x, y ϵ Vn. [e] = ( e1, … , en ) x = ni = 1 iei = ( e1, … , en ) y = nj = 1 jej = ( e1, … , en ) F( x, y ) AeF = || aij ||nxn; [e^] = ( e^1, … , e^n ); x = ni = 1 ^ie^i = ( e^1, … , e^n )^; y = nj = 1 ^je^j = ( e^1, … , e^n )^; [e]: F( x, y ) AeF F( x, y ) = ( )TAeF( ); F( x, y ) = ( ^ )TAe^F( ^ ); Пусть S – матрица перехода от [e] к [e^] ( 1…n ) = S( ^1…^n ); = S^; ( 1…n ) = S( ^1…^n ); = S^; F( x, y ) = ( ) TAe^F( ) = [( ^ )TST]AeF( S^ ) = = ( ^ )T( STAeFS ) ^ ( ) T = ( S^ )T = ( ^ )TST; F( x, y ) = ( ^ )TAeF( ^ ); В силу единственности: Ae^F = STAeFS.
|
|
30.Квадратичные формы в линейном пространстве, полярная билинейная форма. Приведение квадратичной формы к каноническому виду по методу Лагранжа. Пусть V – действительное линейное пространство. Определение 7. Пусть F( x, y ) – симметричная билинейная форма на линейном пространстве V. Числовая функция q( x ), полученная из F( x, y ) путём замены y на x ( т. е. q( x ) = F( x, x )) называется квадратичной формой на V. Билинейная форма F( x, y ) называется полярной к квадратичной форме q( x ). Свойство квадратичной формы: Между квадратичными формами и симметричными билинейными формами на V взаимно-однозначное соответствие. F( x, y ) q( x ). Определение 8. Матрицей Aeq квадратичной формы q( x ) в базисе [e] называется матрица полярной ей билинейной формы F( x, y ) в базисе [e]. q( x ) Aeq = AeF. Vn; [e] = ( e1, … , en ); x = ni = 1 iei; q( x ) = ni, j = 1 aijij; aij = aji; i, j = 1, …, n. q = ni = 1aij( i )2 + 2ni = 1aijij Определение 9. Говорят, что в базисе e^1, …, e^n квадратичная форма имеет канонический вид, если q( x ) = λ1( 1 )2 + λ2( 2 )2 + … + λn( n )2, где x = ni = 1ie^i. В этом случае базис [e^] называется каноническим. Теорема 2. ( Метод Лагранжа ). Пусть в некотором базисе квадратичная форма F( x, y ) задаётся в виде: q( x ) = ni, j = 1 aijij; ( aij = aji, x = ni = 1iei ) Тогда в Vn базис [e^] = ( e^1, …,e^n ) в котором квадратичная форма имеет канонический вид: q( x ) = λ1( 1 )2 + λ2( 2 )2 + … + λn( n )2, где x = ni = 1ie^i. |
31.1.Закон инерции квадратичных форм. Классификация квадратичных форм. Критерий Сильвестра положительной определенности квадратичных форм. Теорема 3. ( Закон инерции ). Число положительных и отрицательных коэффициентов в нормальном виде квадратичной формы не зависит от базиса, в котором квадратичная форма приведена к нормальному виду. Т. е. [e^] = ( e^1, …, e^n ). x = ni = 1^ie^i; q( x ) = ( ^1 )2 + … + ( ^p^ )2 – ( ^p^+1 )2 -…- ( ^p^+q^ )2; p^ + q^ n. [e~] = ( e~1, …, e~n ); x = ni = 1~ie~i; q( x ) = ( ~1 )2 + … + ( ~p~ )2 - ( ~p~+1 )2 - … - ( ~p~+q~ )2; p~ + q~ n; т. е. p^ = p~; q^ = q~; (Без док-ва). Определение 11. Пусть в некотором каноническом базисе квадратичная форма q( x ) имеет вид: q( x ) = ( 1 )2 + … + ( p )2 - ( p+1 )2 - … - ( p+q )2; тогда число положительных коэффициентов в нормальном виде ( p ) называется положительным индексом инерции q( x ), а число отрицательных коэффициентов ( q ) – отрицательным индексом инерции. p + q n. Определение 12. Квадратичная форма q( x ), заданная на действительном линейном пространстве, называется: 1) Положительно определённой, если x V, x : q( x ) > 0; 2) Отрицательно определённой, если x V, x : q( x ) < 0; 3) Знакопеременной, если x, y V: q( x ) >0, q( y ) < 0; 4) Положительно полуопределённой, если x V: q( x ) 0 и y V, y : q( y ) = 0; 5) Отрицательно определённой, если x V: q( x ) 0 и y V, y : q( y ) = 0; |
|
31.2.Закон инерции квадратичных форм. Классификация квадратичных форм. Критерий Сильвестра положительной определенности квадратичных форм. Теорема 4. Пусть квадратичная форма q( x ) задана на действительном конечномерном пространстве Vn, p и q – её положительный и отрицательный индексы инерции, тогда квадратичная форма: 1) положительно определена <=> p = n, q = 0; 2) отрицательно определена <=> p = 0, q = n; 3) знакопеременная <=> p > 0, q > 0; 4) положительно полуопределена <=> 0 < p < n, q = 0; 5) отрицательно полуопределенна <=> p = 0, 0 < q < n. ( Без док-ва ). Vn; e1, … , en – произвольный базис; x = ni=1iei; q( x ) – квадратичная форма. Aiq – матрица q( x ) в [e]; q( x ) = ni, j = 1 aijij. ( a11 a12 … a1n ) Aiq = ( a21 a22 … a2n ) ( ……………… ) ( an1 an2 … ann ) Определение 13. Величины d1 = a11; d22 = M( 1 2 ) = ( a11 a12 ) ( 1 2 ) = ( a21 a22 ); dk = M( 1, …, k ) = | a11 a12 … a1k | ( 1, …, k ) = | ak1 ak2 … akk |, …,
dn = |Aeq| = | a11 … a1n | | an1 … ann | называются главными минорами матрицы Aeq. |
31.3.Закон инерции квадратичных форм. Классификация квадратичных форм. Критерий Сильвестра положительной определенности квадратичных форм. Теорема 5 ( Критерий Сильвестра ). 1) Квадратичная форма q( x ) на Vn является положительно определённой т. и т. т., когда все её главные миноры положительны. ( Т. е. k = 1, …, n: dk > 0 ). 2) Квадратичная форма q( x ) на Vn является отрицательно определённой т. и т. т., когда знаки её главных миноров чередуются, причём d1 < 0. ( Т. е. k = 1, …, n: ( -1 )kdk > 0 ). Пример: V2; n = 2; x = x1e1 + x2 e2; q( x ) = Ax12 + 2Bx1x2 + Cx22; ( A B ) Aq = ( B C ) 1) Положительно определена q( x ) > 0 <=> d1 = A > 0; | A B | d2 = | B C | = AC – B2 > 0. 2) Отрицательно определена q( x ) < 0 <=> d1 = A < 0; | A B | d2 = | B C | = AC * B2 > 0. 3) Знакопеременная | A B | d2 = | B C | < 0; 4) В остальных случаях q( x ) полуопределена. ( Без док-ва ). |
|
32.Определение евклидова пространства. Норма вектора. Неравенство Коши - Буняковского и неравенство треугольника. Угол между двумя векторами. Определение: действительное линейное пространство V называется евклидовым пространством, если в нём любым элементам x,yєV поставлено в соответствие действительное число (x,y) называется скалярным произведением элементов x и y. При этом выполняется следующие условия: x,y,zєV и λєR 1)(x,y)=(y,x) 2)(x+y,z)=(x,z)+(y,z) 3)(λx,y)=λ(x,y) 4)xєV; x≠0 (x,x)>0 Свойства: 1)(x,θ)=0 (x,θ)=(θ,x)=(θ*x,x)=0(x,x)=0; 2)(x,λy)=(λy,x)=λ(y,x)=λ(x,y); 3)(x,y+z)=(x,y)+(x,z) 4)x1,…,xk,
xєV,
y1,…,yk,
yєV,λ1,…,λkєR
( Замечание: 1)Скалярное произведение является билинейной симметричной формой на V соответствует квадратная форма q(x)=(x,x) положительно определена 2)Евклидово пространство – линейное пространство 3)Обозначение Е – евклидово пространство, En-n-мерное евклидово пространство Определение:
пусть
Е-евклидово пространство. Нормой
вектора xєE
называется число равное ||x||= Свойства нормы: 1)xєE:||x||≥0; ||x||=0 x=θ 2)xєE, λєR; ||λx||=|λ|*||x|| 3)Нер-во Коши-Буняковского: x,yєE:|(x,y)|≤||x||*||y||; (x,y)2≤(x,x)*(y,y) 4)Неравенство треугольника: x,yєE:||x+y||≤||x||+||y|| Определение:
пусть x≠θ,
y≠θ;
x,yєE;
Углом между векторами x
и y
называется число, равное φ=arccos |
33.Ортонормированные базисы (ОНБ) евклидова пространства. Теорема о существовании ОНБ, процесс ортогонализации Шмидта. Определение:
векторы
x,yєE
называются ортогональными (x Теорема: всякая ортогональная система ненулевых векторов линейно независима. Определение:
система
векторов е1,…,еnєE
называется ортонормированной, если
I,j=1,…,m:(еi,ej)=δij= Определение: упорядоченная система векторов e1…enєE называется ортонормированным базисом пространства Е, если 1)система векторов e1…en– ортонормированна 2) e1…en- базис E Следствие: в n-мерном евклидовом пространстве любая упорядоченная ортонормированная система из n векторов образует ОНБ. Теорема: пусть f1,f2,…,fm-линейнонезависимая система векторов в евклидовом пространстве Е. L{ f1,f2,…,fm}-линейная оболочка, тогда в L{ f1,f2,…,fm}ОНБ
|
|
34.Ортогональные матрицы, их свойства. Переход от одного ОНБ к другому в евклидовом пространстве. Определение: действительная квадратичная матрица порядка n называется ортогональной, если QQT=QTQ=En, где QT- матрица транспонированная к Q. Свойства ортогональных матриц: 1)если Q-ортогональны, то detQ=1 2)Q-обратима, Q-1=QT 3)Матрица А является ортогональной тогда и только тогда, когда скалярный квадрат каждого столбца этой матрицы равен 1, а скалярное произведение любых двух разных столбцов равно 0. 4)Свойство, аналогичное 3) справедливо для строк. 5)Если Q-ортогональная, то Q-1-тоже ортогональная 6)Если Q,R-ортогональные матрицы, то Q*R-ортогональная матрица. En
[e]:e1,…,en-ОНБ
[ Теорема: ортогональные матрицы и только они являются матрицами перехода от одного ОНБ к другому. |
35.Самосопряженнные операторы в евклидовом пространстве, их свойства. Определение: оператор А евклидова пространства En называется самосопряжённым, если x,yєEn: (Ax,y)=(x,Ay). Свойства: 1)Оператор А является самосопряжённым тогда и только тогда, когда i,j=1,…,n (Aei,ej)=(ei,Aej). 2)Оператор А является самосопряжённым тогда и только тогда, когда матрица Ае в произвольном ОНБ является симметричной. 3)Все корни характеристического многочлена симметричной матрицы действительные числа. 4)Всякий самосопряжённый оператор имеет собственный вектор. 5)Собственные вектора, относящиеся к различным значениям самосопряжённого оператора ортогональны.
|
|
36.Спектральная теорема самосопряженного оператора. Теорема: линейный оператор А евклидова пространства Еn является самосопряжённым тогда и только тогда, когда в Еn ОНБ, состоящий из собственных векторов оператора А. Свойства
1)dim 2) 3)yє 4) |
37.Приведение квадратичной формы к главным осям в евклидовом пространстве. [e]-ОНБ:
А->Ae,
q(x)-> [ Лемма:
если матрица
линейного оператора и квадратичная
форма совпадают в каком-нибудь ОНБ,
то их матрицы совпадают в любом другом
ОНБ. Если Ае= Определение:
говорят, что квадратичная форма q(x)
приводится к главным осям в евклидовом
пространстве Еn,
если в Еn
существует ОНБ в котором квадратичная
форма q(x)
имеет канонический вид, т.е.
q(x)=λ1(ξ1)2+…+λn(ξn)2,
где x= Теорема: всякая квадратичная форма приводится к главным осям. |
|
37. Достаточные условия экстремума функции многих переменных. Теор. Пусть функция U = f(M) = f(x1,...,xn) один раз дифференцируема в окресности точки M0= (x10,...,xn0) и 2 раза дифференцируема в самой точке M0. Пусть эта точка M0 является стационарной точкой функции U = f(M). Т.е. dU(M0) = 0. Тогда если второй диференциал d²U(M0) представляет собой квадратичную форму от диференциала dx1,...dxn является знакоопределенной квадратичной формой, то функция f(M) имеет в точке M0 экстремум, причем если d²U(M0) > 0 – то min, если d²U(M0) < 0 - то max. Если d²U(M0) - знакопеременная квадратичная форма, то экстремума нет. Дока-во. 1. Пусть d²U(M0) - положительно определенная квадратичная форма от dx1,...,dxn. Докажем, что в этом случае M0 – точка локального min. Разложим U = f(M) в окресности точки M0 по локальной формуле Тейлора в виде: ∆U = dU(M0) + (1/2!)* d2U(M0) + o(ρ2) (1), где ∆U = f(M) – f(M0), ρ = ((x1 – x10)2 + ... + (xn - xn0). 2)1/2 = (dx12 + ... + dxn2)1/2 (2) Здесь все условия о разложении функции в M0 по формуле Тейлора с остаточным членом в форме Пеано – выполнены. Т.к. M0 – стационарная точка, то dU(M0) = 0; ∆U = dU(M0) + (1/2!)* d2U(M0) + o(ρ2)= (1/2)*i=1∑n*k=1∑n (aik(xi – xi0)(xk – xk0) + o(ρ2)) (3), где aik = aki = ∂²U/∂xi∂xk (4) Достаточ доказат, что. при достаточно малых ρ правая часть (3) положитлна. Введем обозн-я: hi = (xi – xi0)/ρ ; | hi | ≤ 1; h12 + ... + hn2 = 1 (5) С помощью этих обозначений выражение (3) переходит в |
|
|
|
|
|
|
|



 (r
единиц по главной диагонали).
(r
единиц по главной диагонали).
 =Δ≠0;
=Δ≠0;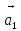 ,…,
,…, – матрицы А базисные по теореме о
базисном миноре строки
– матрицы А базисные по теореме о
базисном миноре строки
 ,…,
,…, линейно выражаются через базисные,
т.е. все уравнения системы являются
линейной комбинацией первых r
уравнений.
линейно выражаются через базисные,
т.е. все уравнения системы являются
линейной комбинацией первых r
уравнений.
 (1)
(1) (2)
(2) ≠0, поэтому при заданных значениях
свободных неизвестных главные
определяются однозначно(по теореме
Крамера)
≠0, поэтому при заданных значениях
свободных неизвестных главные
определяются однозначно(по теореме
Крамера) +…+cn-r
+…+cn-r n-r
n-r ,
, ,єV:
,єV: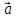 +
+ =
= +
+ 2)
2) ,
, ,
, єV(
єV( +
+ )+
)+ =
= +(
+( +
+ )
3)
)
3) ,
, +
+ =
=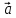 4)
4)
 :
: +
+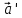 =
= ;
5)α(
;
5)α( +
+ )=α
)=α +α
+α ;
5)(α+β)
;
5)(α+β) =α
=α +β
+β ;
7)(αβ)
;
7)(αβ) =α(β
=α(β );
); =
= ;
Линейное пространство – абстрактное
векторное пространство, элементы
называются векторами. Свойства:
;
Линейное пространство – абстрактное
векторное пространство, элементы
называются векторами. Свойства: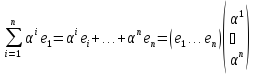 называется разложением элемента x
по базису e1,…,en
называется разложением элемента x
по базису e1,…,en
 ]:
x=
]:
x= =(e1…en)
=(e1…en) и x=
и x= =(
=( 1…
1… n)
n) ;
x=(e1…en)
;
x=(e1…en) =(
=( 1…
1… n)
n) =((e1…en)T)
=((e1…en)T) =(e1…en)[T
=(e1…en)[T ]
]

 ]
называется квадратная матрица порядка
n
в j-ом
столбце которой стоят координаты
вектора
]
называется квадратная матрица порядка
n
в j-ом
столбце которой стоят координаты
вектора
 j
в базисе e,
т.е. j-ого
вектора базиса [
j
в базисе e,
т.е. j-ого
вектора базиса [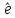 ]
в базисе [e].
[e]=(e1…en)-базис
I; [
]
в базисе [e].
[e]=(e1…en)-базис
I; [ ]=(
]=( )-базис
II; (
)-базис
II; ( )
=(e1…en)T;
)
=(e1…en)T;
 =(e1…en)
=(e1…en)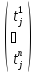 j=1…n; T=||
j=1…n; T=|| ;
;
 ],
то матрица перехода от [
],
то матрица перехода от [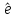 ]
к [e]
будет матрицей T-1.
]
к [e]
будет матрицей T-1. .
. V2-прямая
суммы подпространств V1
и V2.
V2-прямая
суммы подпространств V1
и V2. V2
представляется в виде: x=x1+x2,
где x1єV1
и x2єV2
единственным способом.
V2
представляется в виде: x=x1+x2,
где x1єV1
и x2єV2
единственным способом. V2)
тогда и только тогда, когда:
V2)
тогда и только тогда, когда: =(e1…en)
=(e1…en) =(e1…en)
=(e1…en) ;
Ax=y=
;
Ax=y= =(e1…en)
=(e1…en) =(e1…en)
=(e1…en)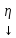 ;
y=(e1…en)
;
y=(e1…en)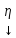 =Ax=A((e1…en)
=Ax=A((e1…en) ;)=(e1…en)(Ae
;)=(e1…en)(Ae );
);
 =A
=A ;
; ]=(
]=( 1,…,
1,…, n)-базис
II;
T-матрица
перехода от [e]
к [
n)-базис
II;
T-матрица
перехода от [e]
к [ ];
(
];
( 1,…,
1,…, n)=
(e1,…,en)T;
AєL(Vn)
=> [e]:A->Ae
A(e1…en)=(e1…en)Ae;
[
n)=
(e1,…,en)T;
AєL(Vn)
=> [e]:A->Ae
A(e1…en)=(e1…en)Ae;
[ ]:A->A
]:A->A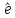 A(
A( 1…
1… n)=(
n)=( 1…
1… n)A
n)A ;
; 1…
1… n)=
A((e1…en)T)=
(e1…en)AeT;
n)=
A((e1…en)T)=
(e1…en)AeT; 1…
1… n)=
(
n)=
( 1…
1… n)
A
n)
A =((e1…en)T)Ae;
(e1…en)AeT=(e1…en)A
=((e1…en)T)Ae;
(e1…en)AeT=(e1…en)A TAeT=TA
TAeT=TA ;
т.к.
detT≠0, то
существует
T-1;
;
т.к.
detT≠0, то
существует
T-1; =T-1AeT;
=T-1AeT; =(
=(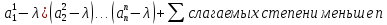
 - диагональная матрица.
- диагональная матрица. =
= ,
(x,
,
(x, =
=

 ;
определение корректно, если
;
определение корректно, если
 ||x,y||≤||x||*||y||-
неравенство Коши-Буньяковского
||x,y||≤||x||*||y||-
неравенство Коши-Буньяковского y),
если (x,y)=0
система векторов пространства Е
называется ортогональной системой,
если все векторы этой системы попарно
ортогональны.
y),
если (x,y)=0
система векторов пространства Е
называется ортогональной системой,
если все векторы этой системы попарно
ортогональны.
 ]:
]: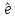 1,…,
1,…, n-ОНБ.
Пусть Q-матрица
перехода от [e]
к [
n-ОНБ.
Пусть Q-матрица
перехода от [e]
к [ ],
т.е. (
],
т.е. ( 1,…,
1,…, n)=(e1,…,en)Q;
Q=||qem||nn;
n)=(e1,…,en)Q;
Q=||qem||nn;
 k=
k= ;
;
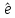 m=
m= ;
(
;
( k,
k, m)=δkm=
m)=δkm= ;
;
 :
:
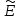 =n-1
=n-1
 -евклидово
пространство.
-евклидово
пространство.
 тогда и только тогда, когда (е1,y)=0
тогда и только тогда, когда (е1,y)=0
 инвариантно относительно оператора
А, т.е. yє
инвариантно относительно оператора
А, т.е. yє :
Ayє
:
Ayє

 ]-ОНБ:
А->
]-ОНБ:
А-> ,
q(x)->
,
q(x)->
 ,
то
,
то
 =
= )
) iei
iei