lecture1

ЗАДАЧИ ДИСКРЕТНОГО ПРОГРАММИРОВАНИЯ

1. Метод ветвей и границ. Задача коммивояжера.

М ногие задачи теории принятия решений описываются математическими моделями дискретного программирования.

Рассмотрим общую задачу математического программирования:

Если множество D является конечным или счетным, то условие – это условие дискретности и данная задача является задачей дискретного программирования.

Среди задач дискретного программирования можно выделить класс экстремальных комбинаторных задач. В данных задачах необходимо найти экстремум некоторой целевой функции, заданной на конечном множестве, элементами которого являются перестановки из n объектов.

Для разрешения комбинаторных задач разработан ряд комбинаторных методов, и наиболее распространенным методом в этой группе является метод ветвей и границ, который основан на последовательном разбиении допустимого множества на подмножества (ветвлений) и вычислении оценок (границ), позволяющий отбрасывать подмножество заведомо на содержащие оптимумы решений.

§Общая схема метода ветвей и границ.

Итак, рассмотрим комбинаторную задачу:

В основу метода ветвей и границ положены следующие построения позволяющие в ряде случаев уменьшить объем перебора вариантов решений.

1. Вычисление нижней границы (оценки) целевой функции f(x)

Иногда удается для 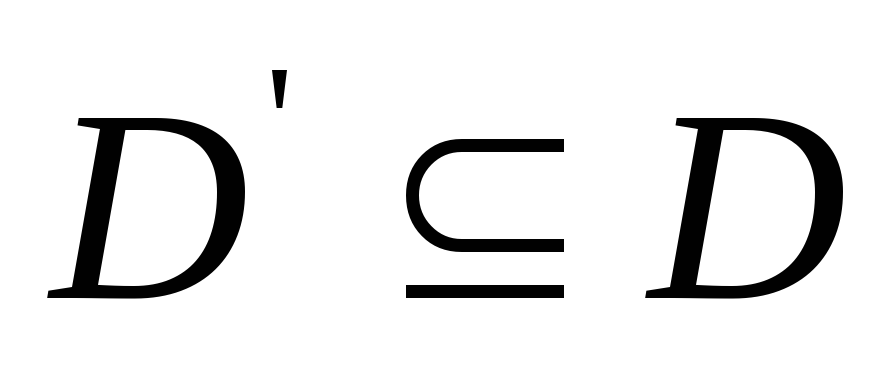вычислить нижнюю оценку целевой функции f(x), такую что:

2. Ветвление (разбиение на подмножества)

Реализация метода связана с разбиением множества D на попарно непересекающиеся подмножества.

Ветвление происходит по следующей схеме:

Шаг 0. Исходное множество D=D⁰, разбиваем некоторым способом на конечное число непересекающихся подмножеств , т.е. при этом .

Получаем начальное дерево разбиения с корнем D⁰ и листьями :

Ш аг k (k>=1). Пусть к началу k-го шага имеется семейство множеств {D^k_i} еще не подвергающихся разбиению. Им соответствуют висячие вершины дерева вариантов. По некоторому правилу, выбираются одно из множеств D^k_v и это множество вновь разбивается на конечное число подмножеств.

3. Пересчет оценок.

Е сли , то

Поэтому, разбивая в процессе решения множество D⁰ на подмножества всегда считают, что оценка для любого из них не меньше оценок для исходного множества D⁰, т.е.

4. Нахождение планов.

Способы построения допустимых решений зависят от специфики задачи.

5. Признак оптимальности.

Имеем разбиение , где {D_i}– cемейство множеств еще неподвергающихся ветвлению (висячие вершины). Если существует такое D_v и решение

То х^* - оптимальное решение , такое что , то x^* – оптмальное решение.

Предлагается на самостоятельное доказательство (доказательство следует из определения оценки ).

6. Оценка точности приближенного решения.

Пусть

Если , то .

Если невелика, то

Невелика, то х можно принять за приближенное решение, а Δ – оценка его точности.

§Алгоритм метода

Шаг 0. Вычисляется оценка ξ(D).

if (при этом удается найти такое допустимое решение )

then х^* – оптимальное решение, stop.

else (если такого допустимого решения найти не удается)

then подвергаем множество D ветвлению: . Вычисляем оценки ξ(D_i), i=1..S.

Ш аг k (k>=1).

Пусть , де {D_i} – семейство множеств, еще не подвергавшихся ветвлению, им соответствуют висячие вершины дерева вариантов.

If (удается найти такое множество D_v в этом семействе и такое допустимое решение , такое что )

then x^* – оптимальное решение. Stop!

else для дальнейшего разбиения выбираем наиболее перспективное множествоD_v по правилу .

D_v разбиваем на непересекающиеся подмножества D_v1,…,D_vk. Вычисляются оценки ξ(D_vj). И переходим к (k+1)-ой итерации.

Замечание: при реализации описанной выше общей схемы метода ветвей и границ для отдельных задач дискретного программирования необходимо разрабатывать правила ветвления, способы вычисления оценок и нахождение допустимых решений, исходя из специфики конкретных задач.

§Задача коммивояжера

Реальная ситуация:

Имеется сеть населенных пунктов(городов) в количестве n штук. Имеется бродячий торговец – коммивояжер. Ему надо посетить все n городов по своим торговым делам. Расстояние между городами ему известно. Его цель минимизировать расходы на передвижение и посетить все n городов. Это означает, что он не должен посещать один и тот же город дважды. И традиционно полагается, что он должен вернуться в исходную точку.

Содержательная постановка:

Требуется найти замкнутый маршрут, проходящий через каждый город ровно один раз (такой маршрут называется маршрутом коммивояжера) и имеющий минимальную суммарную длину (под длиной маршрута понимается сумма длин всех входящих в него проездов из города в город).

Теоретико-графическая модель:

Пронумеруем города числами от i=1..n. Каждому i ставим в соответствие в вершину графа G. Задаем матрицу расстояний С=[C_ij]_nxn, C_ij – расстояние от города i до города j, ребро (i,j) в G. G – полный взвешенный граф(все вершины попарно смежны, каждому ребру соответствует некоторое число(расстояние)). В общем случае .

С =.

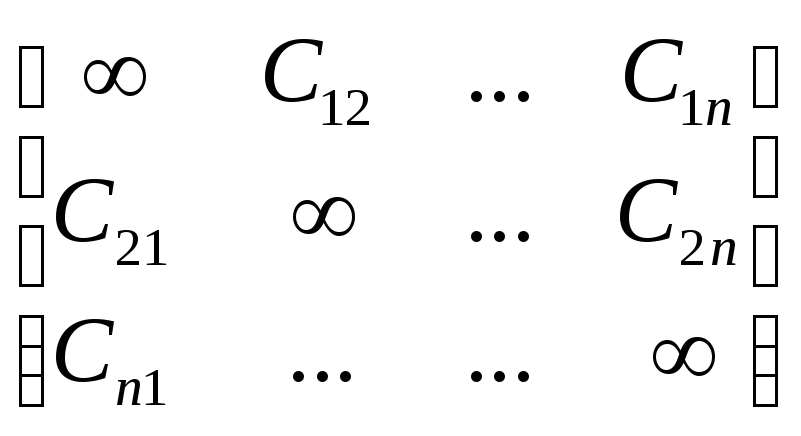Определение: Гамильтоновым циклом в графе называется замкнутый маршрут проходящий по всем вершинам ровно один раз.

Итак, задача сводится к поиску гамильтонового цикла минимальной длины в полном взвешенном графе G.

Пусть х=(i₁,i₂,…,i_n,i₁) – допустимый гамильтоновый цикл (допустимый маршрут коммивояжера), l(x)=C_i1C_i2+C_i2C_i3+…+C_ini1 – длина маршрута.

Задача коммивояжера относится к классу задач комбинаторной оптимизации. Задачи отличаются тем, что их решение конечно.

Математическая модель:

Пусть , тогда математическая модель задачи имеет следующий вид:

г де – произвольные целые неотрицательные числа.

§ Метод ветвей и границ для задачи коммивояжера.

Основные построения.

1. Задание множества D.

D={множество всех Гамильтоновых циклов в графе G}.

2. Вычисление оценки для D.

Рассмотрим некоторый Гамильтоновый цикл x=(i₁,i₂,…,i_n,i₁), его длина l(x)=C_i1i2+C_i2i3+…+C_ini1.

Положим , тогда . При этом .

Положим , тогда . При этом .

Этот процесс называется приведением матрицы C=[C_ij]. Полученная в итоге матрица C’’=[C^”_ij] называется приведенной.

Величины α_i , β_j – называются константами приведения.

Таким образом, приведенная матрица C” получается из С, вычитанием из всех элементов каждой строки минимального элемента этой строки, а затем из всех элементов столбца, минимального элемента этого столбца.

Матрица C” обладает одним замечательным свойством, у нее в каждой строке и в каждом столбце имеется хотя бы один нулевой элемент.

Положим – это нижняя оценка множества D. Ясно, что .

Теорема. Оптимальное решение ЗК с матрицей C” является также оптимальным и для ЗК с матрицей С. При этом длина пути l(x), соответствующего матрице С и длина пути l^”(x), соответствующего матрицы C” связаны соотношением l(x)=l^”(x)+ξ(D).

Доказательство: очевидно из построения оценки ξ(D), длина маршрутов уменьшается на одну и ту же величину ξ(D).

3. Выбор множества для ветвления.

Каждой висячей вершине соответствует своя оценка ξ и своя приведенная матрица C^”. Из семейства множеств, еще не подвергавшихся ветвлению (висячие вершины дерева), выбирается множество D^’ c наименьшей оценкой.

На начальном шаге это множество D (D^’=D).

4. Ветвление.

Множество D^’ всегда разбивается на два непересекающихся подмножества , где D’₁={множество Гамильтоновых циклов содержащих дугу (p, q)}, D’₂={множество Гамильтоновых циклов не содержащих дугу (p, q)}.

Выбор дуги (p,q): Дуга (p,q) выбирается таким образом, чтобы множество D’₁ c наибольшей вероятностью содержало оптимальный цикл, а множество D’₂ – не содержало.

Естественно выбрать (p,q), такое что C”_pq=0, при этом выбор надо сделать таким образом, чтобы циклы входящие в множество D’₂ были как можно длиннее, т.е. по определению D’₂ из пункта p переходим в некоторый пункт i≠j, а в пункт q попадаем из некоторого пункта j≠p.

Очевидно, что длина этого пути будет не меньше чем . Таким образом выбираем (p,q) такую, что .

4. П реобразование матрицы расстояний. Пересчет оценок.

Пусть C”( D’₁) – матрица соответствующая D’₁, ξ(D’₁) – его оценка, С”( D’₂) – матрица соответствующая D’₂, ξ(D’₂) – его оценка .

1. C”( D’₂) получается из С”, полагая c”_pq =∞ и выполняется процедура приведения.

При этом сумма приводящих констант равна ∆(p,q), тогда оценка множества ξ(D’₂) = ξ(D’)+ ∆(p,q).

2. C”( D’₁) – получается из C” путем вычеркивания р-ой строки и q-ого столбца. Кроме того необходимо запретить некоторые элементы, для исключения из множества D’₁ замкнутых маршрутов , проходящих по уже включенным в Гамильтоновый цикл дугам, но не содержащих все n городов (обычно С”_pq =∞). И плюс процедура приведения матрицы. Оценка .

И так далее.

Ветвление продолжают до тех пор, пока одно из множеств не будет содержать только один Гамильтоновый цикл, и нижняя оценка этого множества будет минимальной.

7