
шпоры
.docx|
1.Основные понятия и определения
Устройство наз-ся автоматическим, если оно выполняет свои основные функции самостоятельно без вмешательства человека. Агрегат в котором протекает процесс подлежащий регулированию наз-ся регулируемым объектом. Величина которую нужно поддерживать постоянной или изменять по заданному закону наз-ся регулируемой величиной. Автоматически действующее устройство, предназначенное для выполнения задачи регулирования наз-ся автоматическим регулятором. В частном случае роль регулятора может выполнять ЭВМ. Сигналом ошибки наз-ся разность между заданными значением регулируемой величины и его действительным значением. Внешним возмущающим воздействием наз-ся воздействие, приводящее к изменению регулируемой величины. Автоматическим регулированием наз-ся процесс поддержания каких – либо физических величин на постоянном уровне при помощи автоматических регуляторов. Такие системы получили так же название систем автоматической стабилизации. Автоматическим управлением наз-ся процесс изменения каких – либо величин по определенному закону с помощью автоматических регуляторов. Такие системы получили так же название следящие системы. |
3. Преобразование Лапласа и понятие о передаточной функции При
расчетах и проектировании САУ широко
используется преобразование Лапласа,
которое позволяет заменить
дифференциальные уравнения
алгебраическими. Преобразование
Лапласа определяется соотношением Преобразование кратко записывают в виде F(P)=L{f(t)}.Здесь f(t) называется оригиналом, а F(P) – изображением функции f(t). Рассмотрим некоторые свойства и правила преобразования Лапласа: 1.
2.
3. 4 5.
Обычно САУ рассчитываются при нулевых начальных условиях, т.е. входной сигнал прикладывается к системе после установившего режима. Поэтому все члены, зависящие от начальных условий, будут равны нулю. Рассмотрим нахождение преобразования Лапласа линейного дифференциального уравнения второго порядка.
Умножим
левую и правую части уравнения (1.1) на
Используя
сокращенную форму записи, получим:
Используя
свойство линейности и правило
дифференцирования при нулевых начальных
условиях,получим:
Сравнивая
уравнения (1.1) и (1.2), можно заметить,
что формально уравнение (1.2) можно
получить из уравнения (1.1), если в нем
заменить
Так
как уравнение (1.2) является алгебраическим,
то из него найдем отношение:
где
|
2. Принципы регулирования. Управление
– процесс организации целенаправленного
воздействия на объект, в результате
которого объект переходит в требуемое
состояние. Объект управления подвержен
воздействию различных внешних
возмущений, вследствие чего управляемая
величина отклоняется от заданного
значения. Задачей устройства управления
является обеспечение соответствия
управляемой величины заданному
значению путем передачи на ОУ
необходимого упр воздействия. Упр по возмущению. Основано на принципе компенсации возмущений. Управляемый параметр не изменяется, а используется информация о внешнем воздействии. Достоинство – имеется возможность полной компенсации возмущения. Недостаток – нет требуемой точности. Упр по отклонению. Учитывается действительное состояние объекта упр. Явл основным для большинства современных САУ. Недостатки – затруднено упр, возникающее при разработки быстродействующих систем упр. Повышение точности работы у увеличение коэффициента усиления приводит к потере устойчивости. Комбинированное упр. Более высокое качество упр, т. к. информация о значении возмущающего воздействия позволяет устройству упр работать с предвидением , т.е. начинать компенсацию внешнего возмущения, нарушающего нормальную работу объекта упр, раньше чем возникает достаточно большое отклонение. |
|
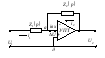
4. Составление уравнения пассивного корректирующего устройства. Очень часто пассивное корректирующее устройство можно представить в виде четырехполюсника (рис.1.1). Здесь Z1(p) и Z2(p) – комплексные сопротивления. Найдем передаточную функцию четырехполюсника. На
основании закона Ома имеем: отсюда
Рассмотрим корректирующее устройство (фильтр)
В этом случае z1(p)=R, z2(p)=1/CP
где T=RC[c]– постоянная времени. Отсюда можно записать дифференциальное уравнение фильтра:
Заменяя
p
на
.
|
6. Передаточная функция УТП Активные
корректирующие устройства обладают
большими возможностями для коррекции,
чем пассивные корректирующие устройства.
Во многих случаях они строятся на базе
усилителей постоянного тока (УПТ),
охваченных глубокой отрицательной
обратной связью. Рассмотрим
идеальный УПТ, у которого коэффициент
усиления
На
основании закона Кирхгофа можно
записать:
отсюда
Подставляя
уравнение (1.4) в уравнение (1.3), получим:
|
8. Моделирование САУ по дифуру.
Алгоритм составления схемы для решения этого уравнения: 1. Запишем ур-е в операторной форме: T2T1P3+(T1+T2)P2UK+ PUK+KUK=KU1 2. Решим уравнение относительно старшей производной (найдем P3UK):
3. Будем считать, что нам известна правая часть этого ур-я. Т.к. U1 необходимо умножить на К1, то это делают с помощью масштабного опер усилителя –К2Р2UK , который тоже умножается на К2. Просуммировав получившиеся величины с помощью суммирующего опер усил на выходе получим сигнал -P3UK, Совместим операцию суммирования с опер интегрирования и на выходе получим 1/Р, затем интегрируем, пока не получим сигнал UK.
|
|
9. Структурный метод моделирования (СММ). Система уравнений практически любой степени сложности состоит из ограниченного числа типовых элементов САУ. К ним относятся: 1. Усилительное звено W(P)=K 2.
Инерционное звено
3.
Колебательное звено
Если ξ=0 звено наз-ся консервативным, на выходе возникают незатухающие колебания 4.
Идеальное интегрирующее звено
5. Идеальное дифференц. звено W(P)=KP Таких звеньев в природе нет, они входят в другие передаточные функции. 6.Реальное
дифференцирующее звено
7.
Инерционное интегрирующее звено
Для каждого типового звена составлена его электронная модель, и в соответствии со СММ в исходной структурной схеме каждое типовое звено заменяется соответствующей электронной моделью, которая соединяется между собой в соответствии со структурной схемой. Различают последовательное соединение звеньев, параллельное соединение звеньев и цепь с местной обратной связью. - Передаточная функция разомкнутой цепи последовательно соединенных звеньев равна произведению передаточных функций всех звеньев. - Передаточная функция разомкнутой цепи из параллельно соединенных звеньев равна сумме передаточных функций всех звеньев.
|
10. Модель инерционного звена. Переходная характеристика имеет вид экспоненты (рис.45), по которой можно определить передаточный коэффициент k, равный установившемуся значению h(t), и постоянную времени Т по времени t, соответствующему точке пересечения касательной к кривой в начале координат с ее асимптотой. При достаточно больших Т звено на начальном участке может рассматриваться как интегрирующее, при малых Т звено приближенно можно рассматривать как безынерционное. Примеры апериодического звена: термопара, электродвигатель, четырехполюсник из сопротивления и емкости или сопротивления и индуктивности. Уравнение и передаточная функция звена имеют вид:
Заменив
Выделяя вещественную и мнимую части, получим:
Амплитудно-фазовая
характеристика Амплитудная и фазовая частотные характеристики строятся по уравнениям:
Изменяя
частоту
|
11. Модель колебательного звена.
Решим относительно старших производной
Колебательное звено является элементарным динамическим звеном второго порядка, обладает тремя варьируемыми параметрами. Колебательным звеном описываются достаточно сложные элементы электромеханических систем и электроприводов, на пример, такой распространенный элемент как электродвигатель постоянного тока. Отличительной особенностью колебательного звена является то, что оно меняет не только свои свойства, но и название в зависимости от величины коэффициента затухания:
|
|
12.
Модель реального дифференцирующего
звена. Идеальное дифференцирующее звено реализовать невозможно, так как величина всплеска выходной величины при подаче на вход единичного ступенчатого воздействия всегда ограничена. На практике используют реальные дифференцирующие звенья, осуществляющие приближенное дифференцирование входного сигнала. Передаточная
функция:
При малых Т звено можно рассматривать как идеальное дифференцирующее. Переходную характеристики можно вывести с помощью формулы Хевисайда:
здесь p1 =-1/T -корень характеристического уравнения D(p) = Tp + 1 = 0; кроме того, D’(p1) = T. При подаче на вход единичного ступенчатого воздействия выходная величина оказывается ограничена по величине и растянута во времени. По переходной характеристике, имеющей вид экспоненты, можно определить передаточный коэффициент k и постоянную времени Т. Примерами таких звеньев могут являться четырехполюсник из сопротивления и емкости или сопротивления и индуктивности, демпфер и т.п. Дифференцирующие звенья являются главным средством, применяемым для улучшения динамических свойств САУ.
|
14. Преобразование структурных схем. Различают последовательное соединение звеньев, параллельное соединение звеньев и цепь с местной обратной связью.При последовательном соединении звеньев.
По определению передаточной функции имеем:
Следовательно,
Цепь из параллельно соединенных звеньев имеет вид (рис. 2.2).
Тогда
Отсюда
т.е. передаточная функция разомкнутой цепи из параллельно соединенных звеньев равна сумме передаточных функций всех звеньев. Структурная схема цепи с местной обратной связью имеет вид (рис. 2.3)
Согласно этой схеме имеем:
Перенеся
Отсюда передаточная функция цепи с обратной связью будет равна:
|
23 Необходимое и достаточное условие устойчивости. Устойчивость характеризует свойства системы возвращаться в исходное состояние после исчезновения сил, которые вывели её из этого состояния , т.е устанавливает факт затухания колебаний . Это означает, что переходный процесс должен затухать. Устойчивость является лишь необходимым, но не достаточным условием работоспособности системы, т.к нам при этом неизвестно время переходного процесса, число колебаний, точность системы, в установившихся и вынужденных режимах. Поэтому на первом этапе проектирования параметры системы выбирают так, чтобы обеспечить устойчивость, а на втором этапе параметры системы и корректирующие устройства выбирают так, чтобы обеспечить заданную точность и желаемый характер переходного процесса
Устойчивость-устанавливает факт восхожд. или затух. колеб. в сист., при этом не известно о времени перех. процесса, числе колеб. за время перех. процесса… Сист. будет устойчива если при t->∞, xперех.(t)->0, т.е. процесс затухает. Общее решение (при отсутствии кратных корней) ищется в виде:
Корни характеристического уравнения могут быть вещественными(+-расходящийся,- - затухаущий), комплекс-ными и чисто мнимыми. Следоват-но устойчивость определяется только общим решением ур-ия (a0dnxвых(t))/dtn+…+anxвых(t)=(b0dnxвх(t))/dtn+…+bnxвх(t), т.е его левой части и не зависит от вх. сигнала. Составл. харак. ур-ие вида: а0рn+a1pn-1+…+an=0; Все корни харак. ур-ия должны нах-ся в левой части комплексной полуплоскости Р, при изменении параметров сист. изменяются значения корней и корни мигрируют на комплексную плоскость. В рез-те чего один или неск-ко корней могут перейти в правую полупоскость и сист. будет неустойчивой.(есть рис.) Для сист. высокого порядка находить корни хар-го ур-ия сложно, поэтому разработаны спец. правила. Эти правила называются критериями устойчивости.
|
|
15. Связь между различными передаточными функциями. Связь между различными передаточными функциями можно найти, если воспользоваться структурной схемой САУ (рис. 2.5).
Здесь обозначено:
По определению передаточной функции имеем:
Перенося в левую часть переменную y(t), получим:
где
Отсюда
можно записать:
Полагая
Если положить F(p)=0, то из этого выражения можно найти передаточную функцию замкнутой системы
Ели положить G(p)=0, то передаточная функция по возмущающему воздействию примет вид:
Передаточная
функция замкнутой системы по ошибке
будет равна:
|
16. Частотные характеристики. Частотные характеристики (ЧХ) определяют динамические свойства звена или системы. Если на вход разомкнутой системы подать гармонический сигнал XBX=XBXSIN(ωt). При прохождении гармонического сигнала ч/з лин сис происходят амплитудные и фазовые искажения, которые можно определить при помощи ЧХ. ХВЫХ=XBЫX SIN(ωt+φ). Заменим вх и вых сигналы на их изображение в виде комплексных чисел: XBX=XBXеJ(ωt) ХВЫХ=XBЫX eJ(ωt+φ) W(Jω) – комплексная частотная ф-ця (аналогия передаточной ф-ции), которая получила название амплитудно-фазовой ЧХ (АФХ). W(Jω)=A(ω)eJφ(ω) A(ω) – амплитудная ЧХ (АЧХ), φ(ω) – фазовая частотная х-ка (ФЧХ). W(Jω) представляет собой комплексное число, в ней можно выделить вещественную и линейную часть - W(Jω)=U(ω)+JV(ω). U(ω) – вещественная ЧХ (ВЧХ), V(ω) – линейная ЧХ (ЛЧХ). Тогда:
- показывает отношение амплитуд вых сигнала к вх для любой частоты воздействия, и позволяет опр амплитудные искажения, вносимые звеном или системой.
- ФЧХ показывает фазовый сдвиг вых сигнала по отношению к вх, и позволяет опр фазовые искажения вносимые звеном. Прологарифмируем W(Jω)=A(ω)eJφ(ω) => lnW(Jω)=lnA(ω)+Jφ(ω) – логарифмическая ЧХ LnA(ω) – логарифм амплитудная х-ка (ЛАХ), φ(ω) – логарифмическая фазовая х-ка. ЧХ позволяют опр источник сигнала, оценивать качество переходного процесса, опр точность САУ, осуществлять синтез корректирующего устройства.
|
17 Логарифмические частотные характеристики Прологарифмируем выражение для амплитудно-фазовой характеристики
Для практических целей удобнее пользоваться десятичными логарифмами и строить отдельно логарифмическую амплитудную частотную характеристику (л.а.х.) и логарифмическую фазовую частотную характеристику (л.ф.х). Для построения л.а.х. находится величина
Эта
величина выражается в децибелах.Для
построения л.а.х. и л.ф.х. используется
стандартная сетка, по оси абсцисс
которой откладывается
По оси ординат откладывается модуль в децибелах. Для этой цели на ней наносится равномерный масштаб. Для построения л.ф.х. используется та же ось абсцисс. По оси ординат откладывается фаза в градусах в линейном масштабе.
Логарифмическая
амплитудная частотная характеристика
инерционного звена определяется
уравнением
а)
при
б)
при
Последняя
будет наклонной прямой с наклоном Наибольшее
ее отклонение от истинной л.а.х. будет
в точке
В инженерных расчетах такой величиной пренебрегают и считают, что логарифмическая амплитудная частотная характеристика апериодического звена имеет вид ломанной, состоящей из двух прямых (рис. 3.5).
|
|
18. Частотные х-ки идеального интегрирующего звена. Уравнение и передаточная функция звена имеют вид:
Частотные характеристики звена показаны на рис.
Логарифмическая
амплитудная частотная характеристика
определяется уравнением Поскольку
на оси абсцисс откладываются значения
|
19 Частотные х-ки идеального диф. звена. Уравнение
и передаточная функция звена: Выражение
для а.ф.х., а.ч.х., ф.ч.х. имеют вид: Их
графики изображены на рис. 3.8 Уравнение
логарифмической амплитудной
характеристики имеет вид: В
отличие от интегрирующего звена, здесь
имеют место положительный наклон
|
|
25Пример критерия Гурвица. Например, найдем условия устойчивости для системы третьего порядка:
Составим матрицу коэффициентов
Для
устойчивости линейной системы третьего
порядка недостаточно положительности
коэффициентов характеристического
уравнения, а дополнительно требуется
выполнение условия
|

 ,
где
,
где
 − комплексная величина, а
− комплексная величина, а
 и
и
 -
вещественные числа.
-
вещественные числа.
 –
–
 –
свойство линейности.
–
свойство линейности.
 –
правило дифференцирования.
–
правило дифференцирования.
 –
правило интегрирования.
–
правило интегрирования.
 –теорема
запаздывания.
–теорема
запаздывания. (1.1)
(1.1) и проинтегрируем от 0 до
и проинтегрируем от 0 до

 .
.
 (1.2)
(1.2) ,где
p
− оператор дифференцирования.
,где
p
− оператор дифференцирования.
 − передаточная функция. Итак,
передаточной функцией называется
отношение преобразования по Лапласу
выходного сигнала к преобразованию
по Лапласу входного сигнала при нулевых
начальных условиях. Для линейной
системы n-ого
порядка передаточная функция будет
равна:
− передаточная функция. Итак,
передаточной функцией называется
отношение преобразования по Лапласу
выходного сигнала к преобразованию
по Лапласу входного сигнала при нулевых
начальных условиях. Для линейной
системы n-ого
порядка передаточная функция будет
равна:

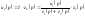 ,
,
 .
.
 ,
, или
или
 .
. ,
получим дифференциальное уравнение:
,
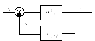
получим дифференциальное уравнение: После
нахождения передаточной функции
фильтра, он изображается на структурных
схемах в виде :
После
нахождения передаточной функции
фильтра, он изображается на структурных
схемах в виде :
 ,
имеет высокое входное сопротивление
и низкое выходное сопротивление. УПТ
с отрицательной обратной Z2(p)
является
замкнутой системой, работающей по
принципу отклонения. Поэтому напряжение
на его входе должно стремится к нулю:
,
имеет высокое входное сопротивление
и низкое выходное сопротивление. УПТ
с отрицательной обратной Z2(p)
является
замкнутой системой, работающей по
принципу отклонения. Поэтому напряжение
на его входе должно стремится к нулю: ,
а i1=i2.Потенциал
точки a
равен потенциалу точки
,
а i1=i2.Потенциал
точки a
равен потенциалу точки
 ,
и поэтому:
,
и поэтому:

 ,
,

 отсюда
передаточная функция УПТ, охваченного
обратной связью, будет равна:
отсюда
передаточная функция УПТ, охваченного
обратной связью, будет равна:
 .
.







 .
. ,
получим выражение для амплитудно-фазовой
частотной характеристики звена:
,
получим выражение для амплитудно-фазовой
частотной характеристики звена: .
. .
.
 .
. от 0 до
от 0 до
 ,
можно построить частотные характеристики
,
можно построить частотные характеристики


 T2P2X2+2ζTPX2+X2=KX1
T2P2X2+2ζTPX2+X2=KX1






 ,
т.е. передаточная функция разомкнутой
цепи последовательно соединенных
звеньев равна произведению передаточных
функций всех звеньев.
,
т.е. передаточная функция разомкнутой
цепи последовательно соединенных
звеньев равна произведению передаточных
функций всех звеньев.
 .
. ,
, :
: .
. в левую часть уравнения, получим:
в левую часть уравнения, получим: .
. .
. 





 − передаточная
функция регулятора;
− передаточная
функция регулятора; − передаточная
функция объекта регулирования.
− передаточная
функция объекта регулирования.
 ,
, − передаточная функция разомкнутой
системы.
− передаточная функция разомкнутой
системы. .
. ,
можно формально перейти к изображениям
по Лапласу и записать последнее
уравнение в виде:
,
можно формально перейти к изображениям
по Лапласу и записать последнее
уравнение в виде:
 .
. .
. .
.


 ;
;
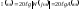 .
. ,
а около меток пишется само значение
частоты
,
а около меток пишется само значение
частоты
 в рад/сек. Масштаб получается
неравномерным. В начале координат
пишется любое значение частоты,
отличное от нуля, т. к.
в рад/сек. Масштаб получается
неравномерным. В начале координат
пишется любое значение частоты,
отличное от нуля, т. к.
 .
Отрезок, соответствующий удесятирению
частоты, называется декадой.
.
Отрезок, соответствующий удесятирению
частоты, называется декадой. Эта
характеристика имеет асимптоты:
Эта
характеристика имеет асимптоты:
 ,
,

 .
. ,а
первая горизонтальной прямой.
Пересекаются в точке
,а
первая горизонтальной прямой.
Пересекаются в точке
 .
. ,
а именно:
,
а именно:
 .
.
 или
или

 .
.



 .
. ,
то мы имеем уравнение прямой, проходящей
через точку
,
то мы имеем уравнение прямой, проходящей
через точку
 при
при
 с наклоном
с наклоном


 .
.



 .
. и положительный фазовый сдвиг. ЛАХ
имеет вид, представленный на рис.
и положительный фазовый сдвиг. ЛАХ
имеет вид, представленный на рис.



 при
при
 .
.
 ,
при
,
при
 .
. .
.